(2020年3月14日)初投稿
(2021年4月19日)オイラーの公式に基づく証明を追加。

ネットからの情報で、私がピタゴラスの定理(Pythagorean theorem)ないしは三平方の定理(Three-square theorem)として知られる法則の証明で使用した図形が三角関数の加法定理の証明にも流用されている展開を知りました。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

いわれてみれば確かに、補助線等の追加でそういう風にも使える訳です。

加法定理の幾何学的証明に挑戦

とりあえず元プログラムに補助線等を追加。

Three_square_theorem04<-function(x){
c0<-c(0,pi/2,-1*pi,-1*pi/2,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,asp=1,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")

#大正方形の頂点{a,b,c,d)
text(c0_cos,c0_sin, labels=c("a","b","c","d",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2))

line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[1]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[1]),length=15)

#小正方形の頂点{ab,bc,cd,da)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x]), labels=c("ab","bc","cd","da"),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2,2))

#塗りつぶし
polygon(c(c0_cos[1],line_scale_04_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_04_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]),#x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]),#y
density=c(30),#塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]),#x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30),#塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]),#x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(0,1,0)) 

#塗りつぶし(加法定理証明用三角形その１)
polygon(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_04_cos[x],line_scale_01_cos[x]),#x
c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_04_sin[x],line_scale_01_sin[x]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=c(200,200,200)) 

#塗りつぶし(加法定理証明用三角形その2)
polygon(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_01_cos[x]),#x
c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_01_sin[x]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=c(200,200,200)) 

#補助線(加法定理証明用)
segments(line_scale_01_cos[x],line_scale_01_sin[x],line_scale_02_cos[x],line_scale_04_sin[x])#ab
segments(line_scale_02_cos[x],line_scale_02_sin[x],line_scale_01_cos[x],line_scale_03_sin[x])#bc
segments(line_scale_03_cos[x], line_scale_03_sin[x],line_scale_04_cos[x],line_scale_02_sin[x])#cd
segments(line_scale_04_cos[x],line_scale_04_sin[x],line_scale_03_cos[x],line_scale_01_sin[x])#da

#補助頂点(加法定理証明用)
text(c(line_scale_02_cos[x],line_scale_01_cos[x],line_scale_04_cos[x],line_scale_03_cos[x]),c(line_scale_04_sin[x],line_scale_03_sin[x],line_scale_02_sin[x],line_scale_01_sin[x]), labels=c("e","f","g","h"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2))
}

角度はこれくらいが丁度良い？

Three_square_theorem04(5)

証明1(線分ab-cdが出発点)

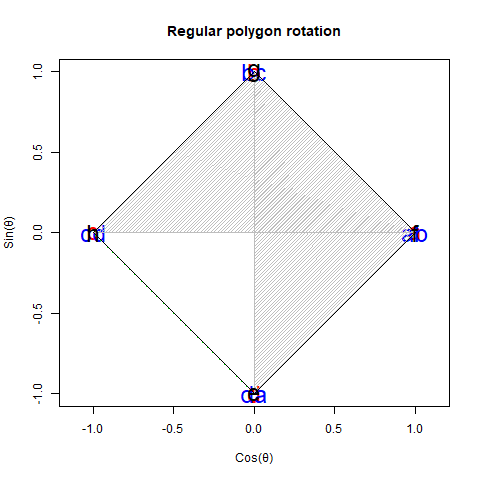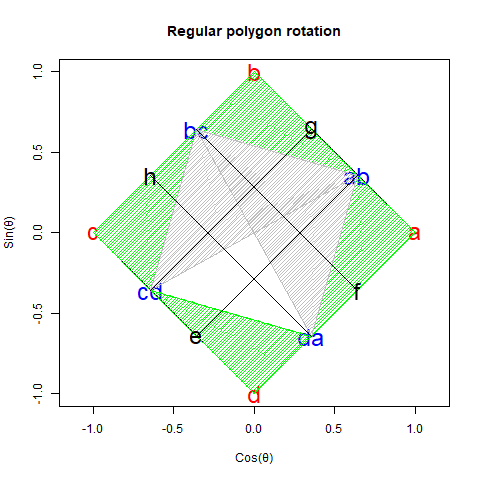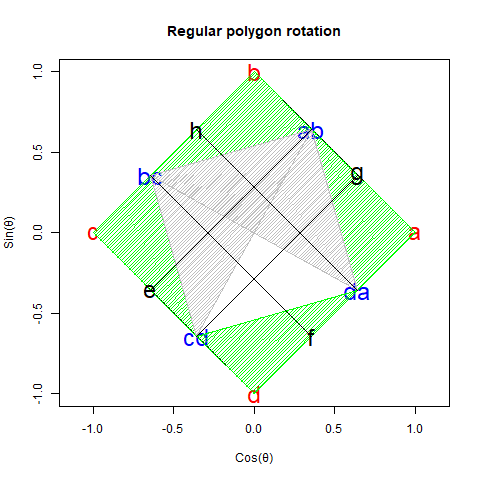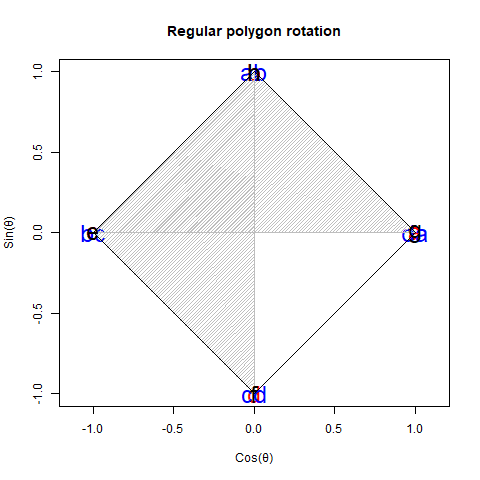
線分ab-cdを１と置く。
次いで角ab-cd-da(以降角αとする)を備える直角三角形ab-cd-daについて線分cd-daの長さをcos(α)、線分da-abの長さをsin(α)と割り振る。
すると角da-cd-d=角ab-da-a(以降角βとする)を備えた直角三角形da-cd-dの線分cd-dの長さがcos(α)×cos(β)、線分da-dの長さがcos(α)×sin(β)、直角三角形ab-da-aの線分da-aの長さがsin(α)×cos(β)、線分ab-aの長さがsin(α)×sin(β)と定まる。
すると角αと角βを足し合わせた結果現れる直角三角形cd-ab-eの線分cd-eの長さはcos(α)×cos(β)-sin(α)×sin(β)(線分cd-dから線分ab-aを引いた結果)、線分_ab-eの長さはsin(α)×cos(β)+cos(α)×sin(β)(線分da-dと線分da-aを足し合わせた結果)となる。

証明2(線分bc-daが出発点)

線分bc-daを１と置く。
次いで角bc-da-ab(以降角αとする)を備える直角三角形bc-da-abについて線分da-abの長さをcos(α)、線分ab-bcの長さをsin(α)と割り振る。
すると角ab-da-a=角bc-ab-b(以降角βとする)を備えた直角三角形ab-da-aの線分da-aの長さがcos(α)×cos(β)、線分ab-aの長さがcos(α)×sin(β)、直角三角形bc-ab-bの線分ab-bの長さがsin(α)×cos(β)、線分bc-bの長さがsin(α)×sin(β)と定まる。
すると角αと角βを足し合わせた結果現れる直角三角形bc-da-fの線分da-fの長さはcos(α)×cos(β)-sin(α)×sin(β)(線分da-aから線分bc-bを引いた結果)、線分_bc-fの長さはsin(α)×cos(β)+cos(α)×sin(β)(線分ab-bと線分ab-aを足し合わせた結果)となる。

証明3(線分cd-abが出発点)

線分cd-abを１と置く。
次いで角cd-ab-bc(以降角αとする)を備える直角三角形cd-ab-bcについて線分ab-bcの長さをcos(α)、線分bc-cdの長さをsin(α)と割り振る。
すると角bc-ab-b=角cd-bc-c(以降角βとする)を備えたを直角三角形bc-ab-bの線分ab-bの長さがcos(α)×cos(β)、線分bc-bの長さがcos(α)×sin(β)、直角三角形_cd-bc-cの線分bc-cの長さがsin(α)×cos(β)、線分cd-cの長さがsin(α)×sin(β)と定まる。
すると角αと角βを足し合わせた結果現れる直角三角形cd-ab-gの線分ab-gの長さはcos(α)×cos(β)-sin(α)×sin(β)(線分ab-bから線分cd-cを引いた結果)、線分_cd-gの長さはsin(α)×cos(β)+cos(α)×sin(β)(線分bc-bに線分cd-cを足し合わせた結果)となる。

証明4(線分da-bcが出発点)

線分da-bcを１と置く。
次いで角da-bc-cd(以降角αとする)を備える直角三角形da-bc-cdについて線分bc-cdの長さをcos(α)、線分da-cdの長さをsin(α)と割り振る。
すると角cd-bc-c=角da-cd-d(以降角βとする)を備えたを直角三角形cd-bc-cの線分bc-cの長さがcos(α)×cos(β)、線分cd-cの長さがcos(α)×sin(β)、直角三角形da-cd-dの線分cd-dの長さがsin(α)×cos(β)、線分da-dの長さがsin(α)×sin(β)と定まる。
すると角αと角βを足し合わせた結果現れる直角三角形bc-da-hの線分bc-hの長さはcos(α)×cos(β)-sin(α)×sin(β)(線分bc-cから線分da-dを引いた結果)、線分_da-hの長さはsin(α)×cos(β)+cos(α)×sin(β)(線分cd-cと線分cd-dを足し合わせた結果)となる。

抽象化すると、こういう事なのです。

	ab-cd	bc-da	cd-ab	da-bc
α	ab-cd-da	bc-da-ab	cd-ab-bc	da-bc-cd
Cos(α)	cd-da	da-ab	ab-bc	bc-cd
Sin（α)	da-ab	ab-bc	bc-cd	da-cd
β1	da-cd-d	ab-da-a	bc-ab-b	cd-bc-c
β2	bc-ab-b	bc-ab-b	cd-bc-c	da-cd-d
Cos(α)Cos(β)	cd-d	da-a	ab-b	bc-c
Cos(α)Sin(β)	da-d	ab-a	bc-b	cd-c
Sin(α)Cos(β)	da-a	ab-b	bc-c	cd-d
Sin(α)Sin(β)	ab-a	bc-b	cd-c	da-d

とどのつまり半径１に対する角度αと角度βの加減算について以下が成立。

まず半径１に対するCos(α)とSin(α)を算出。
次にCos(α)に対するCos(β)とSin(β)、Sin(α)に対するCos(β)とSin(β)を算出。

そしてそれぞれについて以下が成立。

cos(α+β)=cos(α)cos(β)−sin(α)sin(β)
cos(α−β)=cos(α)cos(β)+sin(α)sin(β)
sin(α+β)=sin(α)cos(β)+cos(α)sin(β)
sin(α−β)=sin(α)cos(β)−cos(α)sin(β)

参考サイト：
三角関数の加法定理の証明

#各要素の収集
one<-c("ab-cd","bc-da","cd-ab","da-bc")
alpha<-c("ab-cd-da","bc-da-ab","cd-ab-bc","da-bc-cd")
cos_a<-c("cd-da","da-ab","ab-bc","bc-cd")
sin_a<-c("da-ab","ab-bc","bc-cd","da-cd")
beta01<-c("da-cd-d","ab-da-a","bc-ab-b","cd-bc-c")
beta02<-c("bc-ab-b","bc-ab-b","cd-bc-c","da-cd-d")
cos_a_cos_b<-c("cd-d","da-a","ab-b","bc-c")
cos_a_sin_b<-c("da-d","ab-a","bc-b","cd-c")
sin_a_cos_b<-c("da-a","ab-b","bc-c","cd-d")
sin_a_sin_b<-c("ab-a","bc-b","cd-c","da-d")

#AT=Addition Theorem(加法定理の英訳)
AT<- data.frame(alpha=alpha,cos_a=cos_a,sin_a=sin_a,beta01=beta01,beta02=beta02,cos_a_cos_b=cos_a_cos_b,cos_a_sin_b=cos_a_sin_b,sin_a_cos_b=sin_a_cos_b,sin_a_sin_b=sin_a_sin_b)

#行列変換と型戻し
AT01<-as.data.frame(t(AT))

#各段階の名前設定
colnames(AT01)<-one
rownames(AT01)<-c("α","Cos(α)","Sin（α)","β1","β2","Cos(α)Cos(β)","Cos(α)Sin(β)","Sin(α)Cos(β)","Sin(α)Sin(β)")

#HTML出力
library(xtable)
print(xtable(AT01),type="html")

参考サイト：
Rでデータフレームを転置すると行列になる
具体例として、π/3ラジアン(60度)とπ/6ラジアン(30度)の場合について実際に計算してみました。

#cos(α+β)=cos(α)cos(β)−sin(α)sin(β)
round(cos(pi/3+pi/6),digits=8)
[1] 0
round(cos(pi/3)*cos(pi/6)-sin(pi/3)*sin(pi/6),digits=8)
[1] 0
round(cos(pi/2),digits=8)
[1] 0

#cos(α−β)=cos(α)cos(β)+sin(α)sin(β)
round(cos(pi/3-pi/6),digits=8)
[1] 0.8660254
round(cos(pi/3)*cos(pi/6)+sin(pi/3)*sin(pi/6),digits=8)
[1] 0.8660254
round(cos(pi/6),digits=8)
[1] 0.8660254

#sin(α+β)=sin(α)cos(β)+cos(α)sin(β)
round(sin(pi/3+pi/6),digits=8)
[1] 1
round(sin(pi/3)*cos(pi/6)+cos(pi/3)*sin(pi/6),digits=8)
[1] 1
round(sin(pi/2),digits=8)
[1] 1

#sin(α−β)=sin(α)cos(β)−cos(α)sin(β)
round(sin(pi/3-pi/6),digits=8)
[1] 0.5
round(sin(pi/3)*cos(pi/6)-cos(pi/3)*sin(pi/6),digits=8)
[1] 0.5
round(sin(pi/6),digits=8)
[1] 0.5

この投稿を通じて、それまでチンプンカンプンだった以下のサイトの記述が自然に頭に入ってくる様に。やはり「手を動かす」作業は相応に重要？
折り紙一枚で証明する三角関数の加法定理

それでも正方形は回り続ける？

そういえば、このプログラム、元プログラムの特徴を継承して回転するのです。

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem04(i)
}
}, interval = 0.1, movie.name = "TR04.gif")

全体像を俯瞰するに「正多角形の外接円と内接円」ないしは「円に内接/外接する正多角形」を巡る数理の応用になっている様です。
【初心者向け】挟み撃ち定理による円周率πの近似

一辺の長さがaの正n角形に外接する円の半径r

$r=\frac{a}{2\tan(\frac{π}{n})}$
$a=r(2\tan(\frac{π}{n}))$

一辺の長さがAの正n角形に内接する円の半径R

$R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
$A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$

一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係

1.$r=Rcos(\frac{π}{n})$
2.$R=\frac{r}{cos(\frac{π}{n})}$

外接円を単位円（Unit Circle）としたのが上記アニメーション。

外接円の半径Rは単位円の定義に従って1
これに内接する正多辺形の１辺の長さAは$2\tan(\frac{π}{辺数})cos(\frac{π}{辺数})$
外接円に内接する正多辺形の内接円の半径rは$cos(\frac{π}{辺数})$

この考え方を応用して「外接多角形と内接多角形が角度θで交わる時の関係」に言及したのが加法定理で、正n角形の場合その視座(Perspective)は$\frac{π}{n}$に限定される形となるのです。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

正三角形の場合…単位円に内接する正三角形内で正三角形を回すと、その辺長は2:2と1:2の間を反復し続けるが、その比は多層化された内接円と外接円の半径の推移比にぴったりと重なる。
正方形の場合…単位円に内接する正方形内で正方形を回すと、その辺長はsqrt(2):sqrt(2)と1:2の間を反復し続けるが、その比は多層化された内接円と外接円の半径の推移比にぴったりと重なる。
正五角形の場合…単位円に内接する正五角形の辺長は0.5567581。もはや同心円の連鎖は発生しない。
正六角形の場合…単位円に内接する正六角形の辺長は0.5。やはりもはや同心円の連鎖は発生しない。

オイラーの公式に基づく証明

ここでの記述は以下を参照しています。
【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！

三角関数の加法定理は、オイラーの公式$e^{θi}=\cos(θ)+\sin(θ)i$を用いても証明可能です。

①まずは複素指数関数の掛け算の公式から出発する。

e^{iα}+e^{iβ}=e^{i(α+β)}

②左辺にオイラーの公式を代入する。

(\cos(α)+\sin(α)i)(\cos(β)+\sin(β)i)\\
=(\cos(α)\cos(β)-\sin(α)sin(β))+(\sin(α)\cos(β)+\cos(α)\sin(β))i

②右辺にオイラーの公式を代入する。

\cos(α+β)+\sin(α+β)i

③よって

\cos(α+β)=(\cos(α)\cos(β)-\sin(α)sin(β))\\
\sin(α+β)=(\sin(α)\cos(β)+\cos(α)\sin(β))

最後の(iの除き方を含む)整式過程が面白いですね。

そんな感じで以下続報…

【初心者向け】「加法定理の幾何学的証明」に挑戦。