LoginSignup
0
0

More than 3 years have passed since last update.

@ochimusha01(yasunori matuki)

【オイラーの多面体定理と正多面体】正12面体(Regular Dodecahedron)の作図について。

Last updated at Posted at 2020-04-16

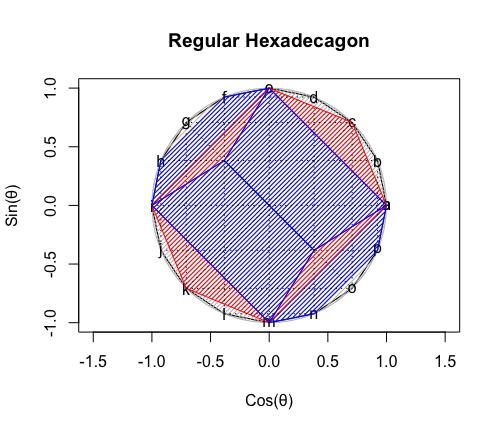
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
square002.gif
この考え方を応用すると正12面体(Regular Dodecahedron)の作図が可能となります。
正十二面体 - Wikipedia
dodecahedron051.gif

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#xy軸上の経度(LoNgitude)座標

#最初の頂点３個x2
LN01=sin(1/5*pi)
c0<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
LNa_cos<-cos(c0)*LN01
LNa_sin<-sin(c0)*LN01

#対蹠側一段目３個
LNd_cos<-cos(c0+pi)*LN01
LNd_sin<-sin(c0+pi)*LN01

#中央の頂点6個x2
LN10=sin(2/5*pi)
c00<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
bx00<-cos(c00+pi/2)
by00<-sin(c00+pi/2)
bx01<-cos(c00+pi*2/5+pi/2)
by01<-sin(c00+pi*2/5+pi/2)
bx02<-c(bx00[1],bx01[1],bx00[2],bx01[2],bx00[3],bx01[3],bx00[4])
by02<-c(by00[1],by01[1],by00[2],by01[2],by00[3],by01[3],by00[4])
LNb_cos<-bx02*LN10
LNb_sin<-by02*LN10

#対蹠側一段目３個
cx00<-cos(c00-pi/2)
cy00<-sin(c00-pi/2)
cx01<-cos(c00+pi*2/5-pi/2)
cy01<-sin(c00+pi*2/5-pi/2)
cx02<-c(cx00[1],cx01[1],cx00[2],cx01[2],cx00[3],cx01[3],cx00[4])
cy02<-c(cy00[1],cy01[1],cy00[2],cy01[2],cy00[3],cy01[3],cy00[4])
LNc_cos<-cx02*LN10
LNc_sin<-cy02*LN10

#立方体におけるz軸上の緯度(LaTitude)座標
LTa=4/5
LTb=2/5
LTc=-2/5
LTd=-4/5

#正12面体描写(原蹠から最初の隣点３個へ)
lines3d(c(portal_i,LNa_cos[1]),c(portal_j,LNa_sin[1]),c(portal_k,LTa),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LNa_cos[2]),c(portal_j,LNa_sin[2]),c(portal_k,LTa),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LNa_cos[3]),c(portal_j,LNa_sin[3]),c(portal_k,LTa),col=rgb(0,0,0),lwd=1)

#正12面体描写(対蹠から最初の隣点３個へ)
lines3d(c(antipordal_i,LNd_cos[1]),c(antipordal_j,LNd_sin[1]),c(antipordal_k,LTd),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LNd_cos[2]),c(antipordal_j,LNd_sin[2]),c(antipordal_k,LTd),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LNd_cos[3]),c(antipordal_j,LNd_sin[3]),c(antipordal_k,LTd),col=rgb(0,0,0),lwd=1)

#正12面体描写(原蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNa_cos[1],LNb_cos[5]),c(LNa_sin[1],LNb_sin[5]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[1],LNb_cos[6]),c(LNa_sin[1],LNb_sin[6]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[1]),c(LNa_sin[2],LNb_sin[1]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[2]),c(LNa_sin[2],LNb_sin[2]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[3]),c(LNa_sin[3],LNb_sin[3]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[4]),c(LNa_sin[3],LNb_sin[4]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)

#正12面体描写(原蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNb_cos[2],LNb_cos[3]),c(LNb_sin[2],LNb_sin[3]),c(LTb,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[4],LNb_cos[5]),c(LNb_sin[4],LNb_sin[5]),c(LTb,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[6],LNb_cos[1]),c(LNb_sin[6],LNb_sin[1]),c(LTb,LTb),col=rgb(0,0,0),lwd=1)

#正12面体描写(対蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNd_cos[1],LNc_cos[5]),c(LNd_sin[1],LNc_sin[5]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[1],LNc_cos[6]),c(LNd_sin[1],LNc_sin[6]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[1]),c(LNd_sin[2],LNc_sin[1]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[2]),c(LNd_sin[2],LNc_sin[2]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[3]),c(LNd_sin[3],LNc_sin[3]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[4]),c(LNd_sin[3],LNc_sin[4]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)

#正12面体描写(対蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNc_cos[2],LNc_cos[3]),c(LNc_sin[2],LNc_sin[3]),c(LTc,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNc_cos[4],LNc_cos[5]),c(LNc_sin[4],LNc_sin[5]),c(LTc,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNc_cos[6],LNc_cos[1]),c(LNc_sin[6],LNc_sin[1]),c(LTc,LTc),col=rgb(0,0,0),lwd=1)

#正12面体描写(原蹠からの経路と対蹠からの経路の結合線6本)
lines3d(c(LNb_cos[1],LNc_cos[4]),c(LNb_sin[1],LNc_sin[4]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[2],LNc_cos[5]),c(LNb_sin[2],LNc_sin[5]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[3],LNc_cos[6]),c(LNb_sin[3],LNc_sin[6]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[4],LNc_cos[1]),c(LNb_sin[4],LNc_sin[1]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[5],LNc_cos[2]),c(LNb_sin[5],LNc_sin[2]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[6],LNc_cos[3]),c(LNb_sin[6],LNc_sin[3]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/dodecahedron051")

ちなみ正十二面体には立方体角線=対蹠のセットが他に9個あり、どれを選んでも同じ結果となります。
dodecahedron002.gif)

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#xy軸上の経度(LoNgitude)座標

#最初の頂点３個x2
LN01=sin(1/5*pi)
c0<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
LNa_cos<-cos(c0)*LN01
LNa_sin<-sin(c0)*LN01

#対蹠側一段目３個
LNd_cos<-cos(c0+pi)*LN01
LNd_sin<-sin(c0+pi)*LN01

#中央の頂点6個x2
LN10=sin(2/5*pi)
c00<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
bx00<-cos(c00+pi/2)
by00<-sin(c00+pi/2)
bx01<-cos(c00+pi*2/5+pi/2)
by01<-sin(c00+pi*2/5+pi/2)
bx02<-c(bx00[1],bx01[1],bx00[2],bx01[2],bx00[3],bx01[3],bx00[4])
by02<-c(by00[1],by01[1],by00[2],by01[2],by00[3],by01[3],by00[4])
LNb_cos<-bx02*LN10
LNb_sin<-by02*LN10

#対蹠側一段目３個
cx00<-cos(c00-pi/2)
cy00<-sin(c00-pi/2)
cx01<-cos(c00+pi*2/5-pi/2)
cy01<-sin(c00+pi*2/5-pi/2)
cx02<-c(cx00[1],cx01[1],cx00[2],cx01[2],cx00[3],cx01[3],cx00[4])
cy02<-c(cy00[1],cy01[1],cy00[2],cy01[2],cy00[3],cy01[3],cy00[4])
LNc_cos<-cx02*LN10
LNc_sin<-cy02*LN10

#立方体におけるz軸上の緯度(LaTitude)座標
LTa=4/5
LTb=2/5
LTc=-2/5
LTd=-4/5

#正12面体描写(原蹠から最初の隣点３個へ)
lines3d(c(portal_i,LNa_cos[1]),c(portal_j,LNa_sin[1]),c(portal_k,LTa),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LNa_cos[2]),c(portal_j,LNa_sin[2]),c(portal_k,LTa),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LNa_cos[3]),c(portal_j,LNa_sin[3]),c(portal_k,LTa),col=rgb(0,0,0),lwd=1)

#正12面体描写(対蹠から最初の隣点３個へ)
lines3d(c(antipordal_i,LNd_cos[1]),c(antipordal_j,LNd_sin[1]),c(antipordal_k,LTd),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LNd_cos[2]),c(antipordal_j,LNd_sin[2]),c(antipordal_k,LTd),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LNd_cos[3]),c(antipordal_j,LNd_sin[3]),c(antipordal_k,LTd),col=rgb(0,0,0),lwd=1)

#正12面体描写(原蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNa_cos[1],LNb_cos[5]),c(LNa_sin[1],LNb_sin[5]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[1],LNb_cos[6]),c(LNa_sin[1],LNb_sin[6]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[1]),c(LNa_sin[2],LNb_sin[1]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[2]),c(LNa_sin[2],LNb_sin[2]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[3]),c(LNa_sin[3],LNb_sin[3]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[4]),c(LNa_sin[3],LNb_sin[4]),c(LTa,LTb),col=rgb(0,0,0),lwd=1)

#正12面体描写(原蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNb_cos[2],LNb_cos[3]),c(LNb_sin[2],LNb_sin[3]),c(LTb,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[4],LNb_cos[5]),c(LNb_sin[4],LNb_sin[5]),c(LTb,LTb),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[6],LNb_cos[1]),c(LNb_sin[6],LNb_sin[1]),c(LTb,LTb),col=rgb(0,0,0),lwd=1)

#正12面体描写(対蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNd_cos[1],LNc_cos[5]),c(LNd_sin[1],LNc_sin[5]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[1],LNc_cos[6]),c(LNd_sin[1],LNc_sin[6]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[1]),c(LNd_sin[2],LNc_sin[1]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[2]),c(LNd_sin[2],LNc_sin[2]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[3]),c(LNd_sin[3],LNc_sin[3]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[4]),c(LNd_sin[3],LNc_sin[4]),c(LTd,LTc),col=rgb(0,0,0),lwd=1)

#正12面体描写(対蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNc_cos[2],LNc_cos[3]),c(LNc_sin[2],LNc_sin[3]),c(LTc,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNc_cos[4],LNc_cos[5]),c(LNc_sin[4],LNc_sin[5]),c(LTc,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNc_cos[6],LNc_cos[1]),c(LNc_sin[6],LNc_sin[1]),c(LTc,LTc),col=rgb(0,0,0),lwd=1)

#正12面体描写(原蹠からの経路と対蹠からの経路の結合線6本)
lines3d(c(LNb_cos[1],LNc_cos[4]),c(LNb_sin[1],LNc_sin[4]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[2],LNc_cos[5]),c(LNb_sin[2],LNc_sin[5]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[3],LNc_cos[6]),c(LNb_sin[3],LNc_sin[6]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[4],LNc_cos[1]),c(LNb_sin[4],LNc_sin[1]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[5],LNc_cos[2]),c(LNb_sin[5],LNc_sin[2]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)
lines3d(c(LNb_cos[6],LNc_cos[3]),c(LNb_sin[6],LNc_sin[3]),c(LTb,LTc),col=rgb(0,0,0),lwd=1)

#追加立方体角線
lines3d(c(LNa_cos[1],LNd_cos[1]),c(LNa_sin[1],LNd_sin[1]),c(LTa,LTd),col=rgb(0,1,0),lwd=1)
lines3d(c(LNa_cos[2],LNd_cos[2]),c(LNa_sin[2],LNd_sin[2]),c(LTa,LTd),col=rgb(0,1,0),lwd=1)
lines3d(c(LNa_cos[3],LNd_cos[3]),c(LNa_sin[3],LNd_sin[3]),c(LTa,LTd),col=rgb(0,1,0),lwd=1)

lines3d(c(LNb_cos[1],LNc_cos[1]),c(LNb_sin[1],LNc_sin[1]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[2],LNc_cos[2]),c(LNb_sin[2],LNc_sin[2]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[3],LNc_cos[3]),c(LNb_sin[3],LNc_sin[3]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[4],LNc_cos[4]),c(LNb_sin[4],LNc_sin[4]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[5],LNc_cos[5]),c(LNb_sin[5],LNc_sin[5]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[6],LNc_cos[6]),c(LNb_sin[6],LNc_sin[6]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/dodecahedron002")

双対（Duality）…(それぞれ三方向に伸びる)頂点と(それぞれ五角形を成す)面の関係を入れ替えると正二十面体(Regular Icosahedron)になります。
【Rで球面幾何学】正20面体(Regular Icosahedron)の作図について。
icosahedron009.gif
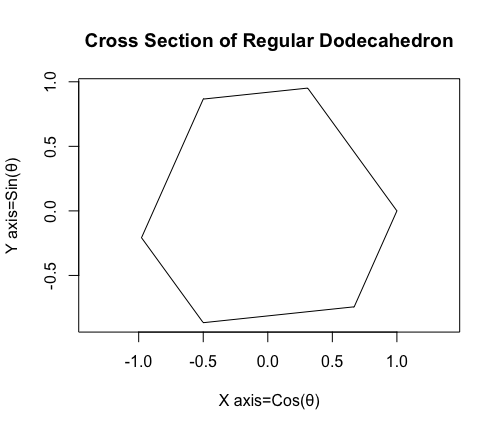
ところで作図上の鍵となるのが、以下の断面(Cross Section)の算出過程。
Rplot11.png

c0<-seq(0,2*pi,length=4)
cx0<-cos(c0)
cy0<-sin(c0)
cx1<-cos(c0+pi*2/5)
cy1<-sin(c0+pi*2/5)
cx2<-c(cx0[1],cx1[1],cx0[2],cx1[2],cx0[3],cx1[3],cx0[4])
cy2<-c(cy0[1],cy1[1],cy0[2],cy1[2],cy0[3],cy1[3],cy0[4])
plot(cx2,cy2,asp=1,type="l"main="Cross Section of Regular Dodecahedron",xlab="X axis=Cos(θ)",ylab="Y axis=Sin(θ)")
  1. まずはガウスの発見した「１の1の冪根の巡回性」に基づいて正三角形を算出。
  2. さらにこれと36度(π/5ラジアン)位相のズレた正三角形を算出して座標をマージする。

背景により深淵な数理が潜んでいる気もしますが、とりあえず以下続報…ちなみに立方体からの屋根掛け法についてはこちら。
【Rで球面幾何学】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)
Rplot25.png
cube_in_dodecahedron19.gif

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0