オイラーの多面体定理(Euler's Polyhedron Theorem)
多面体(Regular Polyhedron)が三次元存在条件(Three-dimensional Existent Condition)を満たすのは
頂点(Vertex)の数-辺(Edge)の数+面(Face)の数=2
なる関係が成立する場合のみである。
様々な図形への「オイラーの多面体定理」適用例
ある頂点か面を選んで始端とし、これに隣接する面を段階的に除去していくと最後にただ一つの終端として頂点か面が残る。要するに2とは最後に残る始端と終端の事である。
逆をいえば、ある頂点か面を選んで始端とし、これから出発する辺や面を段階的に積み上げていって最後にただ一つの終端に到達すればそこに多角形が顕現する事になる。
- (特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作(代表例:正四面体の自己双対(Self Dual)関係、立方体と正八面体、正十二面体と正二十面体の関係)もあるので始端や終端は頂点でも面でもあり得る。
上記により自明の場合(Trival Case)となる通り、ここでいう2なる数字は、その正多角形が外接する円周/球面上の原蹠(PorTal)と対蹠(AntiPordal)に対応しています。実際、以降のプログラムにおいて正多面体は全てこれに準拠するアルゴリズムで描かれているのです。

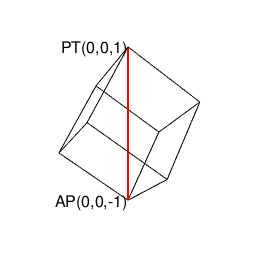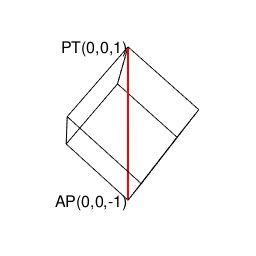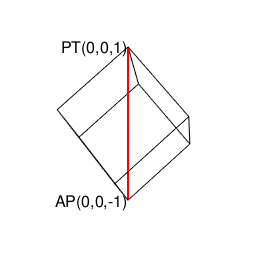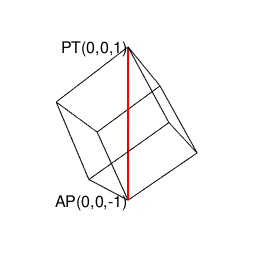
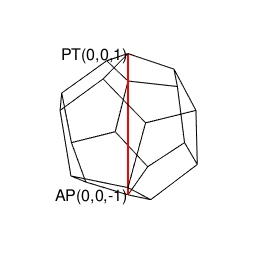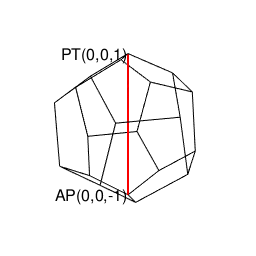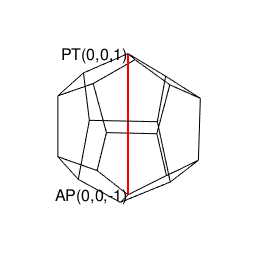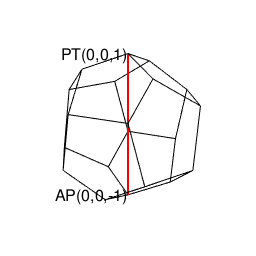
- まず原蹠と対蹠を定め、その正多面体に外接する球表面の立方対角線(Cubic Diagonal)を設定する。
- それに沿った頂点列ごとに断面化し、ガウスの発見した「1の冪乗の巡回性」を用いたアルゴリズム、すなわち
c0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)の構文を用いて座標確定して辺で結ぶ。
どうやってこのアルゴリズムに至るのでしょうか? 今回の投稿はその説明となります。
1辺形(One side)系=奇数系(Odd=2n+1 System)概念(Concept)の出発点。
パスカルの三角形(Pascal's triangle)でいう1段目の「1」。
【初心者向け】パスカルの三角形と二項定理または二項展開
まずは円周/球面上に任意に設定された観測点(Any Point)の対蹠を特定すべく円弧上の観測線(Observation Line)/球面上の円形断面(Circular Section)を「のばす」最初の一歩の段階から話を始めます。この試行(Trial)における観測間隔(Observation Interval)の周期性(Periodicity)が角速度(Angular Velocity)すなわち時間概念の大源流となる点に注意。もちろんこの状態ではまだ「実在する正多面体」はおろか「実在する正多角形」に到達する事も不可能です(頂点数2(1)-辺数1+面数0=1(0)≠2。ちなみにこの解釈では円形断面を面に数えない)。
【Rで球面幾何学】単位円と単位球②円周角(Circumference Angle)とは何か?


原蹠と対蹠関係にある座標が特定されると、その円周/球面上における直径(Diameter)と、その中点座標としての中心(Origin)も、そこから均等な長さで広がる半径(Radius)も自然に自明的に定まります。そしてこれ以降半径=1を計測単位とする単位円(Unit Circle)/単位球面(Unit Sphere)の概念の導入(Introduction)が可能となるのです。
【Rで球面幾何学】単位円と単位球①「半径1」と「直径2」の関係について。
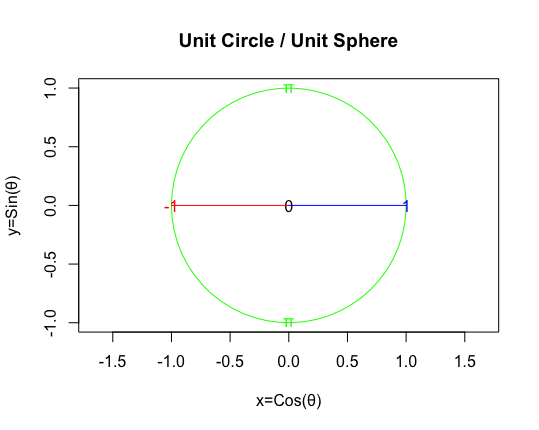
その結果、半径の増減を片側無限算術数列(One-Sided Infinite Arithmetic Sequence)のそれに射影(Projection)する事も可能となります(ただこの辺り「鶏が先か卵が先か」問題を孕む側面も)。
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ

公比(Common Ratio)1を中心とする片側無限幾何数列(One-Sided Infinite Geometric Sequence)の射影に際しては、公比が1より過大だったり過少だったりすると円でなく(0に向けて収束したり、無限大Infに向けて発散する)螺旋軌道を描きます(そう、あたかも軌道設定に失敗した静止衛星の様に…物理学の領域と関連してくる話?)。
【Rで球面幾何学】等比数列(幾何数列)③振動関数を巡る収束と拡散。


もちろん「辺長が無限小(1/Inf)で辺数が無限大(Inf)、円弧/球表面上の任意の点が全て中心からの垂線と直角に交わる円そのもの(Circle Itself)」を直接データ取得元とする事は相変わらず不可能なままですが、多角形による近似が可能となるのがこの時点以降となります(というより、実はあらかじめこちらのデータが用意されていないと円周角の測定自体が遂行不可能)。三角関数(Trigonometric Function)概念の大源流。また測地法(Geodesy)における経度(Longitude)の概念の起源でもあります。
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源

この考え方をより厳密化したのが、半径rをある種のスカラー(Scalar)として扱い、水平方向の角度φと垂直方向の角度θの組み合わせで球表面上の位置を特定する極座標系(Polar Coordinate System)となります。
極座標系 -Wikipedia-

円弧における極座標系
- x=r*cos(φ)
- y=r*sin(φ)
球面上における極座標系
- x=r*cos(φ)*sin(θ)
- y=r*sin(φ)*sin(θ)
- z=r*cos(θ)
さりげなく水平角φと垂直角θの関係設定に三角関数の加法定理(Trigonometric Addition Formulas)の概念が援用されたりしてますね。
【初心者向け】「加法定理の幾何学的証明」に挑戦。
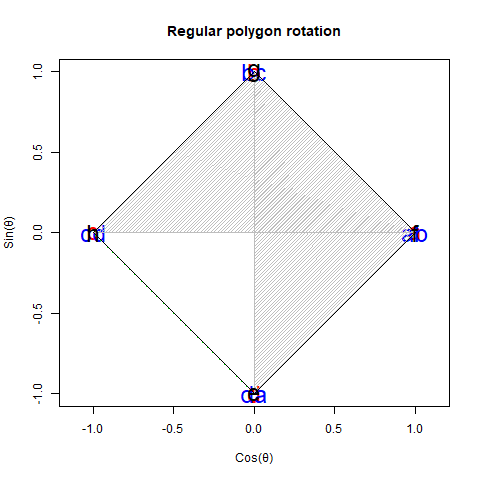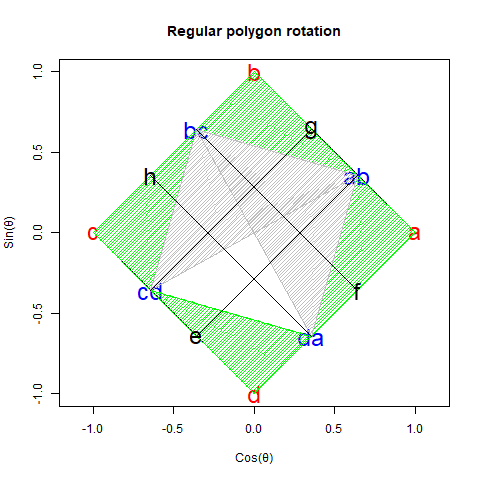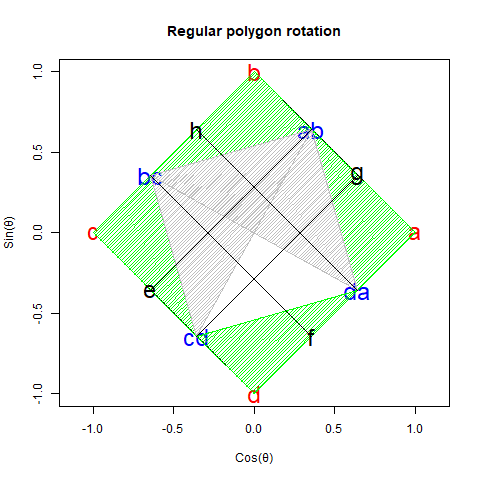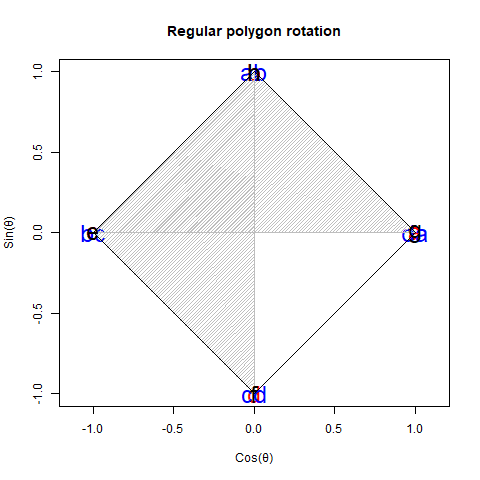
ここでは詳しくは述べませんが、下記に述べる「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」や「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」などの諸概念をこっそり先取りしながら、その事実を上手に誤魔化している感じがします(特に何の説明もなく角度φの範囲が2π、角度θの範囲がπと設定されてる辺り)。ちなみに言うまでもなく上掲の「正多面体を描くアルゴリズム」も、この概念に大きく追っている部分があったりする次第。
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。


いわゆる直交座標系(Rectangular Coordinate System/Orthogonal Coordinate System)概念から連想される貧弱な一次元イメージ(One Dimensional Image)から大きく掛け離れた数理的特質の豊さ。それはまさに(17世紀に成立した)デカルト数学に不満を感じた(主に18世紀から19世紀にかけて急激な発展を遂げた)近世数学界が一つずつ切り拓いてきた研究成果の累積だったといえましょう。さらには以下の様な数理もこれ以降援用可能となります。

①ピタゴラスの定理(Pythagorean Theorem)…直交座標系(Rectangular Coordinate System/Orthogonal Coordinate System)と極座標系(Polar Coordinate System)と(以下に述べる)対蹠座標系(Antipodal Coordinate System)では、それぞれ振る舞いを異にする。というより、その振る舞いの差異こそがそれぞれの座標系の数学的特徴を表している。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

②ガウスの発見した「1の冪乗の巡回性」…これにより人類はコンパスや定規を用いずに任意の正多角形を描ける様になった。またこれにより(収束率自体は大した事ないものの)一般人も手軽に円周率が2πに近似される事を確かめられる様になった。
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似

しかも「1次元上で」展開可能な数理にはさらなる続きがあるのです。
2辺形(Bilateral)系=偶数系(Even=2n System)概念(Concept)の出発点。
①パスカルの三角形(Pascal's triangle)でいう2段目の「1,1」。上掲の対蹠座標系(Antipodal Coordinate System)でいうと出発点の「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」に該当します。
【Rで球面幾何学】パスカルの三角形と二項定理または二項展開
より具体的には、古典的振動関数(Mathematical Oscillation Function)に分類されるy=-1^x辺り。

# 振動関数(Mathematical Oscillation Function)
# 公比D=-1
# -1^xにi^2=-1を代入
# (0+1i)^2^x=(0+1i)^2x
MOF01<-function(index){
z0<-complex(real=0,imaginary=1)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
# cy<-Im(c0)
# 単位円/単位球(Unit Circle / Unit Sphere)
theta <- seq(pi,-pi,length=60)
plot(cos(theta),sin(theta),asp=1,type="l",col=rgb(0,1,0), main="Mathematical Oscillation Function y=-1^x", xlab="x=Cos(θ)", ylab="y=Sin(θ)")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
text(cx,0,"X",cex=2,col=rgb(0,1,0))
}
# アニメーション動作設定
Time_Code<-seq(-1,1,length=30)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF02.gif")
②さらにはパスカルの三角形(Pascal's triangle)でいう3段目の「1,2,1」。上掲の対蹠座標系(Antipodal Coordinate System)でいうと「円弧上に位置する原蹠と対蹠の間を1回だけ直角に曲がって結ぶ2次元処理」に該当します。
【Rで球面幾何学】パスカルの三角形と二項定理または二項展開
上掲の極座標系においてx=cos(φ),y=sin(φ)と表された円弧上の展開。曲がる角度の直角性は正弦定理(Law of Sines)A/sin(a)=B/sin(b)=C/sin(c)=2Rの特殊型たるタレスの定理(Thales' Theorem)「直径に対する円周角は直角である」が保証します。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。
ここで問題となるのが虚数(Imaginary Number)の扱い。例えば物理学の世界が単位円筒(Unit Cylinder)における円描画について、あえて時代に配慮して言葉を濁し「等速円運動(Constant Velocity Circular Motion)を互いに直交するx軸側とy軸側からそれぞれ観測(Observe)すると、同じ波形が互いに位相が90度=π/2ずれた単振動(Simple Vibration)、すなわち(x軸からの観測結果に由来する)余弦波(Cosin wave)と(y軸からの観測結果に由来する)正弦波(Sine wave)が得られる」みたいな微妙な言い回しを伝統的に用いてきたのに対し、数学者オイラーはこれを単一の式にまとめる為にあえてCos(θ)+Sin(θi)なるストレートな明示表現を導入しています。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸(円弧)

XZ軸(Cos波)

YZ軸(Sin波)

【初心者向け】「単位円筒」から「単位球面」へ

また上掲の古典的振動式y=-1^xも、実数直線上を滑らかに動く様にあえてi^2=-1を代入しi^2xの形で用いています。上掲図ではX座標のみ採択しているので直線上の動きに留まっていますが、Y軸上の動きも拾うとやはり円を描いているのです。要するに①と②の差異は「与えられる座標軸の関係上、顕現する範囲」に過ぎないという事になってくるのですね(統計学の徒なら、この話を聞いて真っ先に思い浮かべるべき図形がある筈です。ほら、釣鐘型のアレ…虚数への言及が憚られる時代、あえてそれに言及せず複素平面の概念の有効活用を考えたガウスの渾身の方便…そもそも「一次元なのに面積がsqrt(π)相当」ってどういう状態だと思います?)。
【Rで球面幾何学】等比数列(幾何数列)③振動関数を巡る収束と拡散。

# 振動関数(Mathematical Oscillation Function)
# 公比D=-1
# -1^xにi^2=-1を代入
# (0+1i)^2^x=(0+1i)^2x
MOF01<-function(index){
z0<-complex(real=0,imaginary=1)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
# 単位円/単位球(Unit Circle / Unit Sphere)
theta <- seq(pi,-pi,length=60)
plot(cos(theta),sin(theta),asp=1,type="l",col=rgb(0,1,0), main="Mathematical Oscillation Function y=-1^x", xlab="x=Cos(θ)", ylab="y=Sin(θ)")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
}
# アニメーション動作設定
Time_Code<-seq(-1,1,length=30))
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF03.gif")
こうした混乱の原因は虚数(Imaginary Number)の命名者たるデカルト自身が、自らの座標系においてこうした各次元の独立性を阻害する要因を排除し続ける態度を墨守し続けたからです。しかしながら「ニュートン力学が圧倒的支配力を有する巨視的力場空間と異なり、量子力学が有効となる様な微視的力場空間においては(ニュートン力学の作用で封じられていた)様々な事象が顕現してくる」なる立場に立脚するファインマンの経路積分(Path integral)がコンセンサスとして共有される様になった現代社会においては、むしろオイラーの多面体定理理ついても「確かに三次元存在条件を満たす多面体こそ限られているが、その水面下では(表面化しないだけで)さらに複雑な数理が展開している」と考える方が自然となってしまった訳です。

ところでしばしば2辺形(Bilateral)とも呼ばれるこの図形、辺の設定が面白い事になってます。
- 円弧上だと(0+1i)系と(0-1i)系の共益複素数(Conjugate complex number)の2本(頂点数2+辺数0(1-1)+面数0で一応はオイラーの多面体定理の立体実在条件を満たす)
- 球表面上だと(ピタゴラスの法則によって取得される「半径と同じ長さの辺数」同様に)円近似上の経度分割数と同数。
そして振動関数-1^x(i^2x)においては、これが以下の様に変動していると考える訳です。

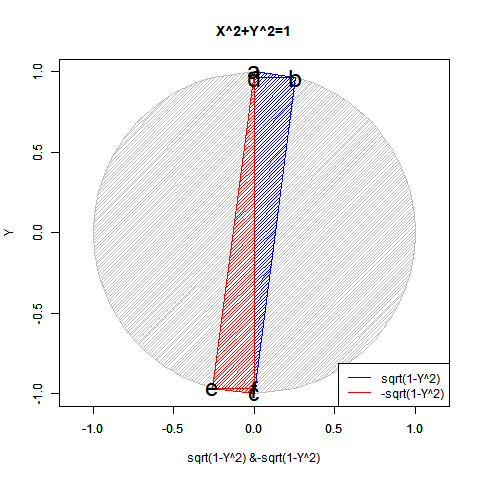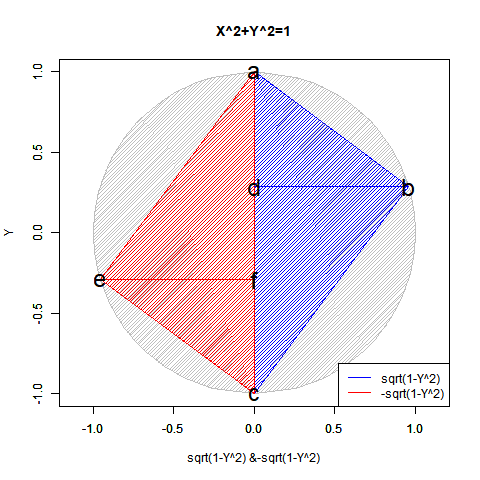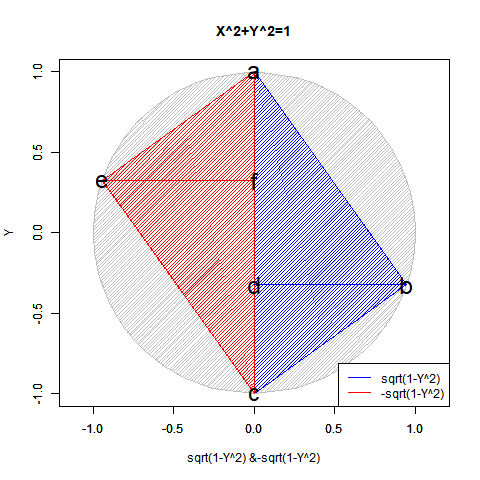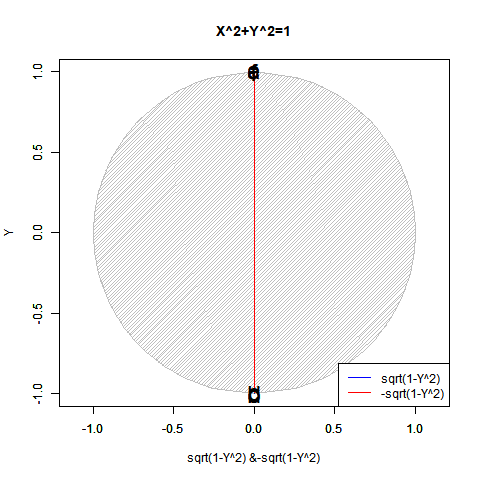
# RD=2角形(Regular Digon)
# Radian=角度(60分割)
RD<-function(Radian){
c0<-seq(0,2*pi,length=60)
c1x<-cos(c0)
c1y<-sin(c0)
plot(c1x,c1y,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Henagon",xlab="cos(θ)",ylab="sin(θ)")
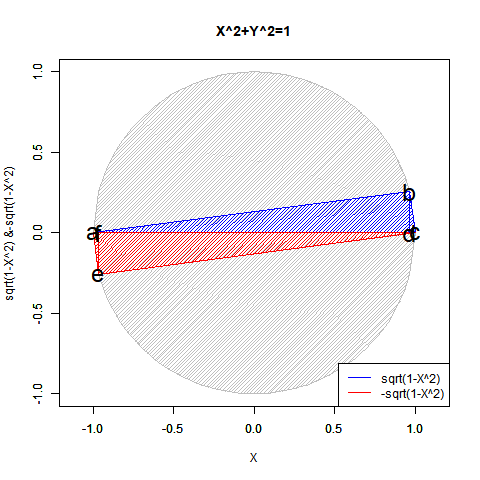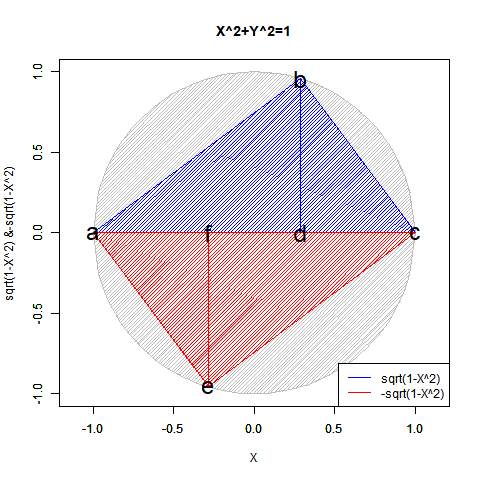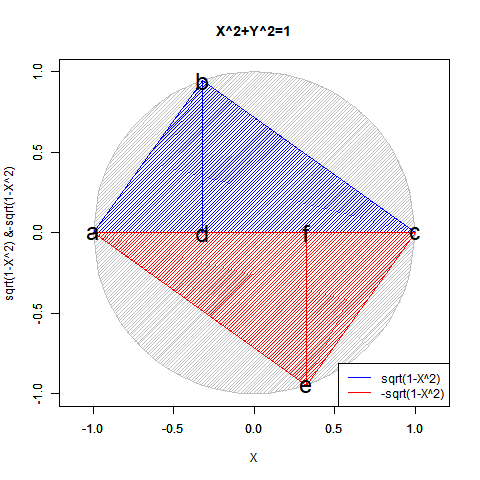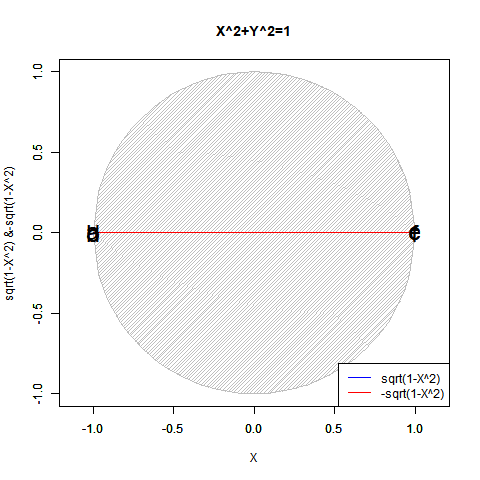
RD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),xlim=c(-1,1),ylim=c(-1,1),main="Regular Henagon",xlab="X",ylab="sqrt(1-X^2) & -sqrt(1-X^2)")
par(new=T)#上書き指定
plot(cx,-1*cy,asp=1,type="l",col=rgb(1,0,0),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
# 緯度(latitude)の描写
lat<-seq(-1,1,length=9)
for(i in lat){
segments(i,f0(i),i,-f0(i),col=c(200,200,200))
}
# 経度(Longitude)の描写
lon<-seq(-pi/2,pi/2,length=9)
for(i in lon){
par(new=T)#上書き指定
plot(cx,sin(i)*cy,asp=1,type="l",col=c(200,200,200),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
}
# 塗りつぶし
p_max<-15
p0<-seq(pi,0,length=p_max)
px_Hi<-rev(cos(p0))
px_Low<-rev(cos(p0*-1))
py_Hi<-rev(sin(p0))
py_Low<-rev(sin(p0*-1))
# 左側インジケータ描画(緑)
polygon(c(px_Hi[1:Radian],px_Low[Radian:1]), #x
c(py_Hi[1:Radian],py_Low[Radian:1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
# 右側インジケータ描画(赤)
polygon(c(px_Hi[p_max:Radian],px_Low[Radian:p_max]), #x
c(py_Hi[p_max:Radian],py_Low[Radian:p_max]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
}
# アニメーション
library("animation")
Time_Code=c(1:15,14:1)
saveGIF({
for (i in Time_Code){
RD(i)
}
}, interval = 0.1, movie.name = "RD01.gif")
-
極座標系における垂直角θや測地法における緯度(Latitude)の様に球表面上の水平断面と組み合わせて任意の位置を指定する座標系においては、かかる変動における往路か復路の半分しか必要としない(半円だけなら-1~0、0~1、1~0、0~-1の4回描いている。そうi^2xだから)。極座標系における水平角φの範囲が2πなのに対し垂直角θの範囲がπだったり、経度が(ロンドンの旧グリニッジ天文台跡を0°とする)東経180°と西経180°で表されるのに対し、緯度が(赤道を0度とする)北緯90度と南緯90度で表されるのはこの為。
-
一方、(ガウスが発見した「1の冪乗の巡回性」を用いて)円弧に内接する正多角形や球表面に内接する正多面体を描画する際には、原則として偶数系の場合には原蹠と対蹠を結ぶ単一図形を、奇数系の場合にはそれぞれ原蹠と対蹠を始点とし、反対側まで届かない一対の図形を描く。ここで重要なのは、この座標系においては(それぞれが球表面上に位置する頂点のみが実体で、それを便宜上を結ぶ)辺や面こそが「想像上の産物(Imaginary Things)」に過ぎないのであり、頂点間の関係の変動によっては結び方の変更も起こり得るという辺り。
【計算上の往復】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

3辺形(Trilateral)系=奇数系(Odd=2n+1 System)概念(Concept)の正念場。
①パスカルの三角形(Pascal's triangle)でいう4段目の「1,3,3,1」に対応。原蹠1と対蹠-1を結ぶ長さ2の立方対角線(Cubic Diagonal)を設定したら、「断面」はそれぞれ「ほぼ」1/3と-1/3辺りに配置される。断面に現れる図形は正三角形。
正四面体(Regular Tetrahedron)
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
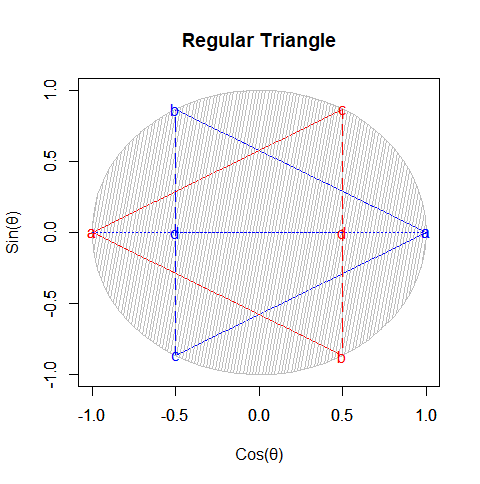

- 頂点数4-辺数6+面数4=2でオイラーの多面体定理を満たす。実在する唯一の奇数系正多面体であり、上掲の説明にある通り「原蹠から出発し対蹠に到達しない図形」と「対蹠から出発し原蹠に到達しない図形」の2つがセットで扱われ、その単位でパスカルの三角形(Pascal's triangle)でいう3段目の「1,3,3,1」に対応する。
- (特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作の結果が同じ正四面体になる自己双対(Self Dual)である。
原蹠や対蹠に集められた正三角形には以下の様な極めて興味深い特徴が見て取れる。
- 単独で平面充填(Tiling)が行える。
- それぞれ三枚集めると四枚目が補完され一対の正四面体が構成される。
- それぞれ四枚集めると原蹠と対蹠を直接結んで単一の正八面体が構成される。
- それぞれ五枚集めると中間に十枚が補完されて原蹠と対蹠を結び単一の正二十面体が構成される。
- 六枚集めると、やはり単独で平面充填(Tiling)が行える正六角形が構成される。
ちなみに正三角形と正六角形は相互に平面上において特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作を行った結果現れる図形でもある。
【Rで球面幾何学】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体(Dodecahedron)との関係について。


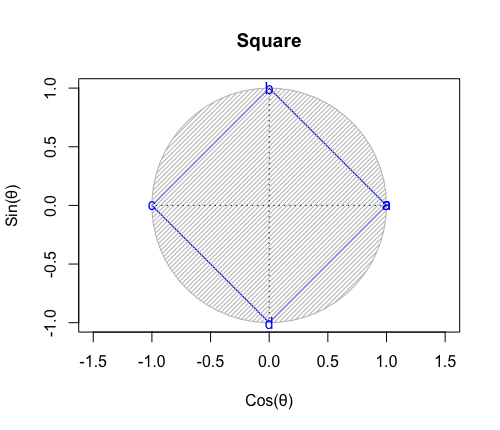

正六面体(Regular Hexahedron/Cube)
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。

- 頂点数8-辺数12+面数6=2でオイラーの多面体定理を満たし(原蹠と対蹠を結ぶ経路を内在する偶数系なので)単体でパスカルの三角形(Pascal's triangle)でいう3段目の「1,3,3,1」に対応する。
- 上掲の対蹠座標系(Antipodal Coordinate System)でいうと「円弧上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ3次元処理」に該当。
- (特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作により正八面体と双対(Duality)関係にある。
この形での実装はハミルトンの四元数(Hamilton's Quaternion)と関係が深く、実際ijk=-1,ij=k,jk=i,ij=k,ji=-k,kj=-i,ji=-kをその表面上で確認可能。それ自体についての幾何学的説明は「原蹠から2回直角に曲がって対蹠に到達するには左右に1回ずつ曲がらねばならない」といった感じになる。
【Rで球面幾何学】ハミルトンの四元数(Hamilton's Quaternion)は何を表しているのか?
| i | j | k | |
|---|---|---|---|
| i | -1 | -k | j |
| j | k | -1 | -i |
| k | -j | i | -1 |
正四面体一対と頂点と辺の数、断面数とそこに現れる多角形(正三角形)が一致しており、上掲の「(頂点間の関係変化に伴う)面の構成の組み替え」の典型例と言えそうなのである。
ちなみに立方体(Cube)を構成する正方形(Square)には、平面上においても特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換しても同型が現れる自己双対(Self Dual)性が備わっている。クラインの四元群(Klein's Quaternion Group)においても(そこで各操作対象の連続性=平面充填性を考慮するなら)概ねその操作対象は正方形と想定される。
クラインの四元群
| e | p | q | r | |
|---|---|---|---|---|
| e | e | p | q | r |
| p | p | e | r | q |
| q | q | r | e | p |
| r | r | q | p | e |
- 操作"e"…何もしない(何もしなかったのと同様の結果)。
- 操作"p"…X軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
- 操作"q"…Y軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
- 操作"r"…Z軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
# クラインの四元群(Klein's Quaternion Group)一覧
epqr<-c("e","p","q","r")
perq<-c("p","e","r","q")
qrep<-c("q","r","e","p")
rqpe<-c("r","q","p","e")
TR01<- data.frame(e=epqr,p=perq,q=qrep,r=rqpe)
colnames(TR01)<-c("e","p","q","r")
rownames(TR01)<-c("e","p","q","r")
library(xtable)
print(xtable(TR01),type="html")
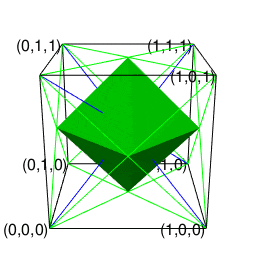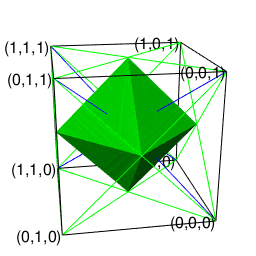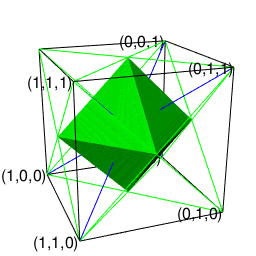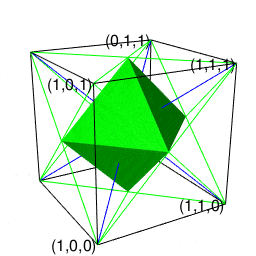
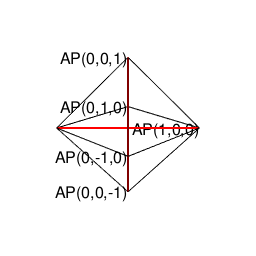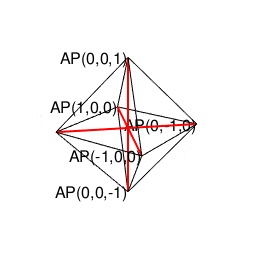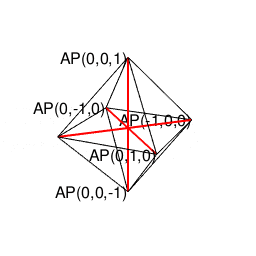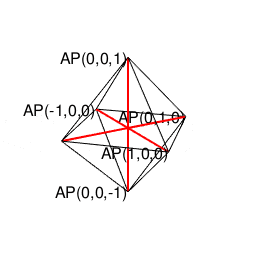
②パスカルの三角形(Pascal's triangle)でいう3段目の「1,2,1」に対応。原蹠1と対蹠-1を結ぶ長さ2の立方対角線(Cubic Diagonal)を設定したら、「断面」はそれぞれ原点近くに1枚だけ配置される(3方向それぞれから見てこの設定になっている)。断面に現れる図形は正方形。
正八面体(Regular Octahedron)
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

- 頂点数6-辺数12+面数8=2でオイラーの多面体定理を満たし(原蹠と対蹠を結ぶ経路を内在する偶数系なので)単体でパスカルの三角形(Pascal's triangle)でいう3段目の「1,2,1」に対応する。
- 上掲の対蹠座標系(Antipodal Coordinate System)でいうと「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」に該当。
- (特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作により正六面体と双対(Duality)関係にある。
あえてこれまで正四面体と正六面体の作図に用いてきた「原蹠と対蹠を結ぶ軸線に沿って両側から三角錐を伸ばす」操作の延長線上において語るなら「底面を1:1:sqrt(2)の2等辺三角形とする一対の三角錐が中間点で合体して原蹠と対蹠を結ぶ経路が確立され、それに合わせて図形全体における頂点・辺・面構造の調整(頂点-2,辺数-2+2,面数-1+3)が遂行された」形となります。
上掲の対蹠座標系(Antipodal Coordinate System)でいうと「円弧上に位置する原蹠と対蹠の間を直角に3回曲がって結ぶ4次元処理」を彷彿とさせるのが興味深いのですが、そこで辿り着くのはあくまで対蹠でなく原蹠。これってどういう事?
四辺形(Quadrilateral)系以上の操作概念を含むかもしれないそれ以外の正多面体について。
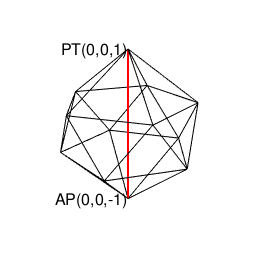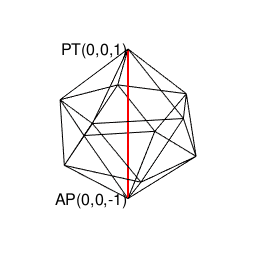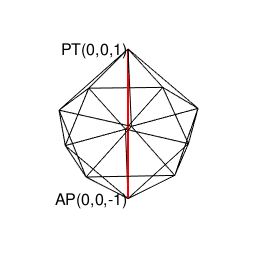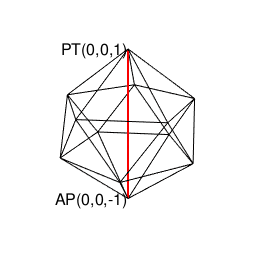
正二十面体(Regular Icosahedron)
【Rで球面幾何学】正20面体(Regular Icosahedron)の作図について。

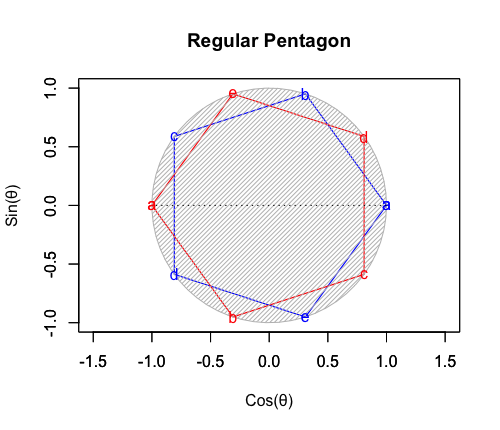
- 原蹠1と対蹠-1を結ぶ長さ2の立方対角線(Cubic Diagonal)を設定したら、「断面」はそれぞれ「ほぼ」1/3と-1/3辺りに配置される。断面に現れる図形は正五角形。
- 頂点数12-辺数30+面数20=2でオイラーの多面体定理を満たす。パスカルの三角形(Pascal's triangle)との対応は不明。
- 上掲の対蹠座標系(Antipodal Coordinate System)でいうと「円弧上に位置する原蹠と対蹠の間を2回曲がって結ぶ3次元処理」に該当(ただし曲がる角度が直角ではない)。
- (特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作により正十二面体と双対(Duality)関係にある。
様々な考察が可能そうですが、とりあえずは以下続報。
正十二面体(Regular Dodecahedron)
【Rで球面幾何学】正12面体(Regular Dodecahedron)の作図について。

- 原蹠1と対蹠-1を結ぶ長さ2の立方対角線(Cubic Diagonal)を設定したら、「断面」はそれぞれ4/5と2/5と-2/5と-4/5辺りに配置される。断面に現れる図形はもはや正多角形ではない。
- 頂点数20-辺数30+面数12=2でオイラーの多面体定理を満たす。パスカルの三角形(Pascal's triangle)との対応は不明。
- 上掲の対蹠座標系(Antipodal Coordinate System)でいうと「円弧上に位置する原蹠と対蹠の間を4回曲がって結ぶ5次元処理」に該当(ただし曲がる角度が直角ではない)。
- (特定の辺数が伸びる)頂点と(同数の辺数を備える)面を交換する双対変換(Dual Transformation)操作により正二十面体と双対(Duality)関係にある。
- さらには古代ギリシャ時代より「屋根掛け」操作によって正六面体と双対関係にあるとされてきたが、この操作の意味は現時点の私には憶測すら不可能。
様々な考察が可能そうですが、やはりとりあえずは以下続報。
とりあえずここまでの総括。
これまでの投稿内容、特に「球面幾何学(Spherical Geometry)」と称してきた部分が相応に整理されてきました。碩学の皆さんにとっては「当たり前の些事」に過ぎないかもしれませんが、つい最近まで単なる文系人間に過ぎなかった私にとっては、こういう一歩一歩積み重ねながらの確認作業が重要となってくるのです。特に初めてやっと「(レヴィ=ストロースが数学者集団ブルバキの援用を受けて「ムルンギン族の婚姻体系の研究」に採用した)クラインの四元群」と「ハミルトンの四元数」について連続的に語れたのが感動ひとしおでした。しかしああ、ついに血塗れの最後を遂げたガロワさんの「群論はいいぞぉ、お前は既にこっちサイドの人間だ」なる呼び声に本格的に捕まってしまった感もないでもなく…
レヴィ・ストロースの「親族の基本構造」における群構造の理解

- 改めて「正二角形」と正三角形と正方形の特異性が確認された形。ところでこれらは同じオイラーが先鞭をつけた「透視図法の世界」すなわち自然指数関数(Natural Exponential Function)や自然対数関数(Natural Logarithmic Function)の概念とも深く関わってくるのである。
- それにつけても、正五角形系数理(Regular pentagonal System)がグイグイ割り込んでくる不思議が止まらない。対数尺(Logarithmic scale)の対象範囲外なのに、どうしてこんなにも誰もが入れ込むの?
【数理Computingの基礎】(人類の限界を乗り越えんとする)N進法/p進数の世界?


こんな感じで以下続報…
