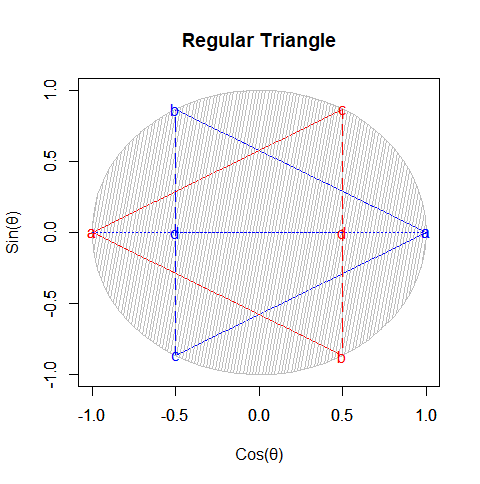
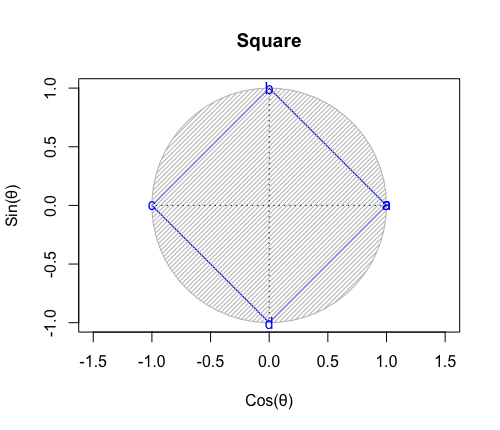
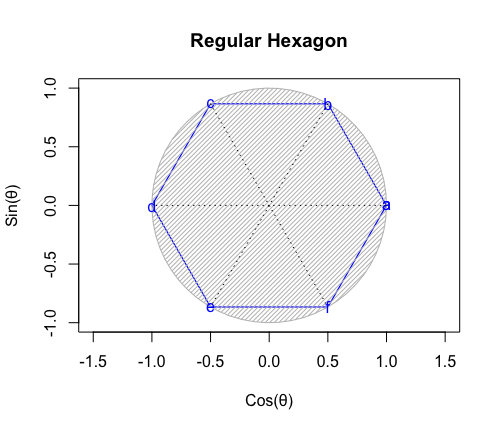
1種類で平面を充填できる正多角形は、正三角形(Equilateral Triangle)、正方形(Square)、正六角形(Hexagon)の3種類のみであり、ピュタゴラスによって証明された。これらは正平面充填形 (Regular Tessellation) とも呼ばれる。
ちなみに正方形は平面上における（特定の辺数が伸びる）頂点と（同数の辺数を備える）面を交換する双対変換(Dual Transformation)操作の結果が同じ正方形になる自己双対(Self Dual)であり、正三角形は同様の操作により正六角形と双対(Duality)の関係にある。平面充填はこの範囲において可能と考えて良い。
ここでいう「正方形は頂点と面を交換する双対変換操作の結果が同じ正方形になる自己双対形であり、どちらも平面充当性を備えている」とは、要するにこういう事です（自明の理の範囲内）。
正方形による平面充填（頂点を基点とした場合）
#Tiling(Plane Filling) by Square(From Vertex)
cx=c(-2,2,2,-2,-2)
cy=c(-2,-2,2,2,-2)
plot(cx,cy,type="l",asp=1,xlim=c(-3,3),ylim=c(-3,3),col=rgb(0,0,1),lwd=2, main="Tiling by Square(From Vertex)",xlab="X axis",ylab="Y axis")
lines(c(-2,2), c(0,0),col=rgb(0,0,1),lwd=2)
lines(c(0,0), c(-2,2),col=rgb(0,0,1),lwd=2)
#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
}
正方形による平面充填（面を基点とした場合）
#Tiling(Plane Filling) by Square(From Face)
cx=c(-3,3,3,-3,-3)
cy=c(-3,-3,3,3,-3)
plot(cx,cy,type="l",asp=1,xlim=c(-3,3),ylim=c(-3,3),col=rgb(0,0,1),lwd=2, main="Tiling by Square(From Face)",xlab="X axis",ylab="Y axis")
lines(c(-3,3), c(-1,-1),col=rgb(0,0,1),lwd=2)
lines(c(-3,3), c(1,1),col=rgb(0,0,1),lwd=2)
lines(c(-1,-1), c(-3,3),col=rgb(0,0,1),lwd=2)
lines(c(1,1), c(-3,3),col=rgb(0,0,1),lwd=2)
#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
}
また、ここでいう「正三角形と正六角形は、頂点と面を交換する双対変換操作によって互いに変換される双対関係にあり、どちらも平面充当性を備えている」とは、要するにこういう事です（自明の理の範囲内）。
正三角形による平面充填（頂点を基点とした場合）
#Tiling(Plane Filling) by Equilateral triangle(From Vertex)
cx=c(-2,-1,1,2,1,-1,-2)
cy=c(0,2,2,0,-2,-2,0)
plot(cx,cy,type="l",asp=1,xlim=c(-2,2),ylim=c(-2,2),col=rgb(0,0,1),lwd=2, main="Tiling by Equilateral triangle(From Vertex)",xlab="X axis",ylab="Y axis")
lines(c(-1,1), c(-2,2),col=rgb(0,0,1),lwd=2)
lines(c(-1,1), c(2,-2),col=rgb(0,0,1),lwd=2)
lines(c(-2,2), c(0,0),col=rgb(0,0,1),lwd=2)
#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
}
正三角形による平面充填（面を基点とした場合）
#Tiling(Plane Filling) by Equilateral triangle(From Face)
cx=c(-2,2,0,-2)
cy=c(1,1,-3,1)
plot(cx,cy,type="l",asp=1,xlim=c(-2,2),ylim=c(-3,1),col=rgb(0,0,1),lwd=2, main="Tiling by Equilateral triangle(From Face)",xlab="X axis",ylab="Y axis")
lines(c(-1,0), c(-1,1),col=rgb(0,0,1),lwd=2)
lines(c(0,1), c(1,-1),col=rgb(0,0,1),lwd=2)
lines(c(-1,1), c(-1,-1),col=rgb(0,0,1),lwd=2)
#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
}
ところで「正p角形における頂点に集まる辺数q個」に注目したシュレーフリ記号{p,q}でそれぞれの正多角形を表すと以下となります。
- 正三角形{3,6}
- 正方形{4,4}
- 正六角形{6,3}
そして正p角形の内角をq倍すると360°(2πラジアン)になることから、(p-2)q=2pとなり、この事からも1種類の正多角形による充填がこの範囲でしか存在しない事が証明出来るとされています（自明の理の範囲内）。
#正三角形{3,6}…ある頂点を中心に正三角形を６個並べると平面充填する。
> (3-2)*6
[1] 6
> 2*3
[1] 6
>
#正方形 {4,4}…正方形を中心に同じ正方形を8個並べると平面充填し自己相似図形となる。
> (4-2)*4
[1] 8
> 2*4
[1] 8
>
#正六角形 {6, 3}…正六角形を中心に正六角形を６個並べると平面充填する。
> (6-2)*3
[1] 12
> 2*6
[1] 12
あれ？「ある頂点を中心に正方形を4個並べると平面充填して自己相似図形となる場合」や「正三角形を中心に同じ正三角形を3個並べると平面充填して自己相似図形となる場合」どこいった？ そして突然現れた２なる数字、もしやオイラーの多面体定理(Euler's Polyhedron Theorem)にも現れる「頭蹠と対蹠のセット」なのでは？
【Rで球面幾何学】オイラーの多面体定理(Euler's Polyhedron Theorem)と平面充填(Tiling)の連続性について。
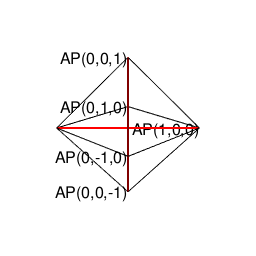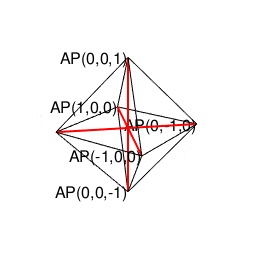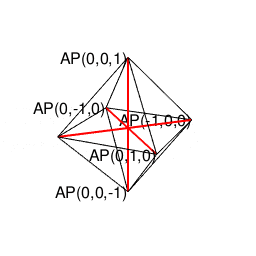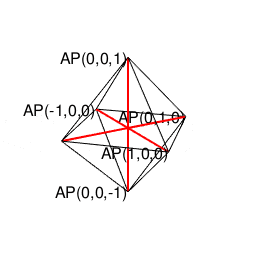
①そう「8個で空間を充填する図形」といえば、単独で空間充填（Space Filling）条件を満たす唯一の正多面体にして「(「右手系」/「左手系」の意味で)左右に1回ずつ直角に曲がると原蹠から対蹠に到達する」正六面体(Regular Hexahedron/Cube)なのである。これ自体は「各頂点から3辺が伸びる図形」であり、その各面の平方対角線(Square Diagonal)はsqrt(2)で立方対角線(Cube Diagonal)はsqrt(3)となる。あれ、頂点から伸びる辺が１本足りないぞ？
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
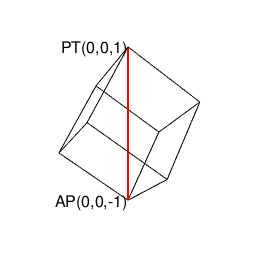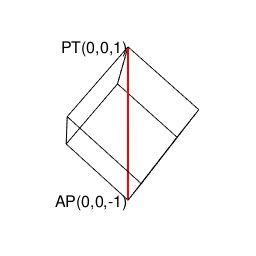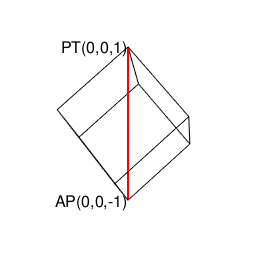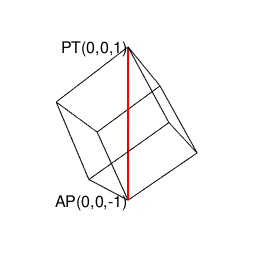
| i | j | k | |
|---|---|---|---|
| i | -1 | -k | j |
| j | k | -1 | -i |
| k | -j | i | -1 |
#正六面体{6,3}…ある頂点を中心に立方体を8個並べると空間充填し自己相似図形となる。
> (6-2)*3
[1] 12
> 2*6
[1] 12
②この正六面体と双対関係にあるのが「各頂点から4辺が伸びる図形」にして「1回直角に曲がると原蹠から対蹠に到達し、3回直角に曲がると原蹠に戻る」正八面体(Regular octahedron)となる。単独では空間充填性を備えず、(一辺がsqrt(2)で高さがsqrt(3)/2の)正四面体(Regular Tetrahedron)による補完を必要とする。そうか、なまじ頂点から伸ばせる辺の数が４本と考えると、こんな問題が…
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
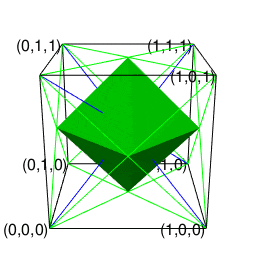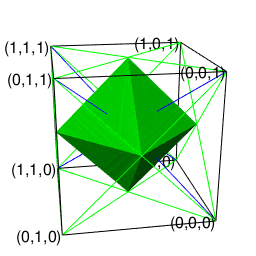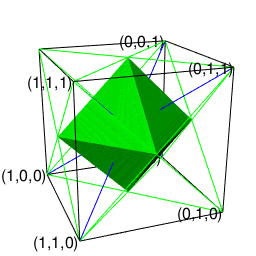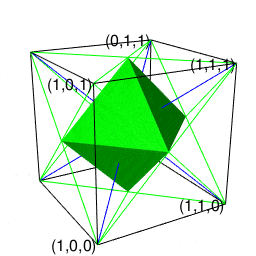
③ところでその正三角形自体は3枚集めると正四面体、4枚集めると正八面体、5枚集めると正二十面体、6枚集めると正六角形を形成する。
【Rで球面幾何学】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。
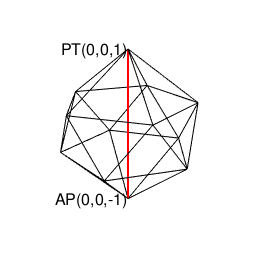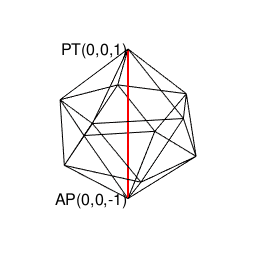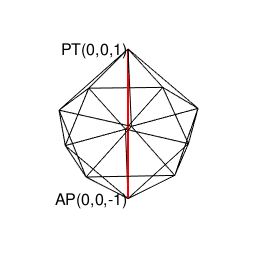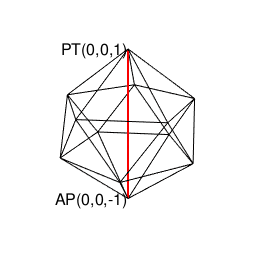
とどのつまり(対蹠座標系上の連続性に甘えて)正八面体と正四面体の補完関係を「誤差の範囲」と割り切り（「5系」の数字が乱入してくる）正二十面体の場合さえ切り捨てたら、とりあえず直交座標系のX軸、X軸、Z軸上に整数集合{-2,-1,0,1,2}と無理数sqrt(2)(X軸1:Y軸1の時の対角線)とsqrt(3)(X軸1:Y軸2かX軸2:Y軸1の時の対角線)しか現れない(要するに原点を中心とする半直線の集合たる直交座標系や、単位円を中心に同心円集合を形成する曲座標系に匹敵する)閉じた座標系(Closed System)が立ち現れてくるのです。
①この「絶天地通」により、その正二十面体と双対関係にあり「それぞれ(「右手系」/「左手系」の意味で)左右に２回ずつ曲がると原蹠から対蹠に到達する5次元操作」が特徴の正十二面体(Regular Dodecahedron)が一緒くたに「認識可能な範囲外を跋扈する絶対他者」の立場に追いやられる事になる。
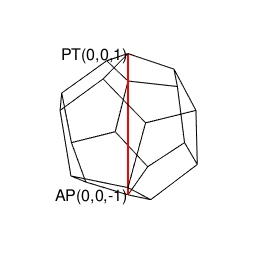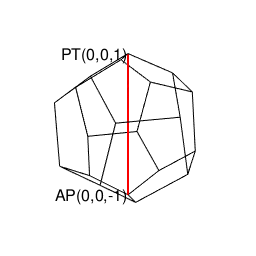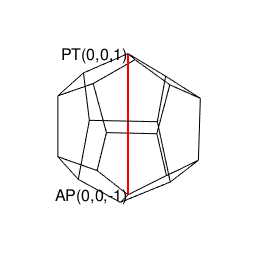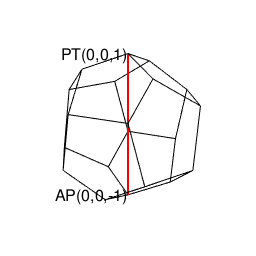
②かかる「隔壁落とし」に満足出来ないのなら「正方形とその縦方向と横方向の180度回転」しか存在しないクラインの四元群の世界まで撤退するしかない（面を起点とする展開のみに注目し、頂点を起点とする展開を完全に切り捨てている）。
クラインの四元群
| e | p | q | r | |
|---|---|---|---|---|
| e | e | p | q | r |
| p | p | e | r | q |
| q | q | r | e | p |
| r | r | q | p | e |
- 操作"e"…何もしない(何もしなかったのと同様の結果)。
- 操作"p"…X軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
- 操作"q"…Y軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
- 操作"r"…Z軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
遂にやっと、これまで心の中でモヤモヤしていた「絶天地通＝誤差切り捨て=隔壁落とし問題」について触れる事が出来ました!! とりあえず、以下続報…