LoginSignup
1
1

More than 3 years have passed since last update.

@ochimusha01(yasunori matuki)

【Rで球面幾何学】指数関数や対数関数における「ネイピア数周期」の意味について。

Last updated at Posted at 2020-05-05

【初心者向け】指数・対数関数の発見
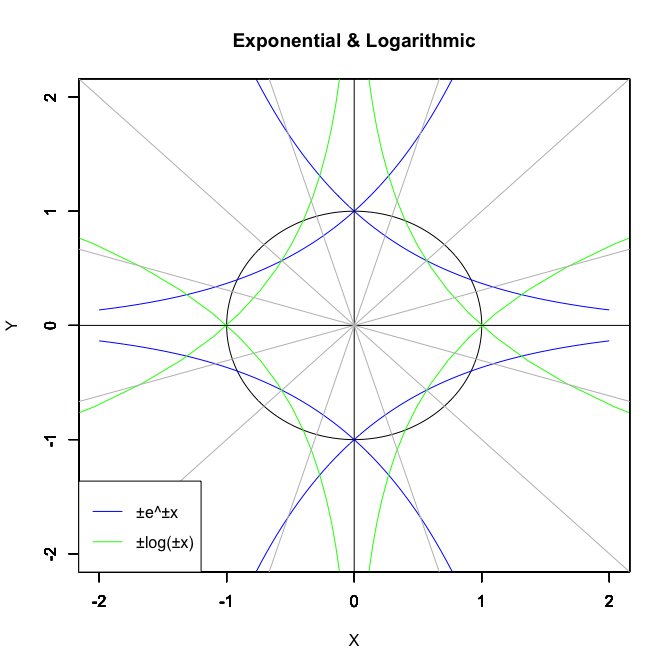
20190927233136 (1).png

ところで指数関数Y=a^Xiや対数関数Y=Log(Xi,base=a)が「ちゃんと１回だけ」円を描くのは底（root）をネイピア数e(exp(1)=2.718282)もしくは1/e(exp(-1)=0.3678794)とする以下の8種類の関数だけだったりします。

  • 自然指数関数e^Xi（exp(x*(0+1i))）あるいは1/e^Xi（exp(-1*(0+1i))）
  • 上の符号を逆転させた自然指数関数-e^Xiあるいは-1/e^Xi
  • 自然対数関数log(Xi)あるいはlog(Xi,base=1/exp(1))
  • 上の符号を逆転させた自然対数関数-log(Xi)あるいは-log(Xi,base=1/exp(1))

そうして描かれる円がどれも「中心座標を0とする半径１の円弧」という辺りも興味深い？

①自然指数関数e^Xi（exp(x*(0+1i))）あるいは1/e^Xi（exp(-1*(0+1i))）の場合

#統計言語Rによる実演例「1/e^Xiとe^Xiの狭間」
root_move_01<-function(rp){

#タイトル定義
Main_title<-c("Alternative to root")
x_title<-c("Real Expanse")
y_title<-c("Imaginaly Expanse")
#関数定義
f1<-function(x){rp^(x*(0+1i))} 
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
Circle_x=Im(f1(theta))
Circle_y=Re(f1(theta))

f2<-function(x){-rp^(x*(0+1i))} 
#f3<-function(x){log(x*(0+1i))}
cnv_y <- c(seq(-3, 3, length=300))
Log_plus <- f1(cnv_y)
#f4<-function(x){-log(x*(0+1i))} 
Log_minus <-f2(cnv_y) 
#f5<-function(x){2*x^2} 
#f6<-function(x){x^2} 
#f7<-function(x){4*x+5} 
#凡例用関数名定義
f1_name<-c("root^xi(x=Real,y=Imaginaly),r=1") 
f2_name<-c("Exponential root^xi,-root^xi")  
f3_name<-c("Logarithmic log(xi, base=root),-log(xi, base=root)")  
#f4_name<-c("2*(x-3)^2") 
#f5_name<-c("2*x^2")  
#f6_name<-c("x^2") 

#グラフのスケール決定
gs_x<-c(-1.7,1.7)
gs_y<-c(-1.7,1.7)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#777777"
#グラフ描画
plot(Circle_x,Circle_y,xlim=gs_x,ylim=gs_y,type="l",col=Black, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(f1,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f2,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_plus, cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_minus,cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
#基準線
abline(h=0,,col=Gray)
abline(v=0,,col=Gray)
#塗りつぶし
polygon(c(Circle_x), #x
c(Circle_y), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　
#凡例描画
legend("bottomleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Black,Blue,Green))
}

根を-1(1/root)から0(root/root)にかけて変化させる->下から上に円弧消失
20190628102302.gif

#-1から0へ
library("animation")
Time_Code=c(exp(-1.0),exp(-0.9),exp(-0.8),exp(-0.7),exp(-0.6),exp(-0.5),exp(-0.4),exp(-0.3),exp(-0.2),exp(-0.1),exp(0.0))
saveGIF({
for (i in Time_Code){
　　root_move_01(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

根を0(root/root)から1(root)にかけて変化させる->上から下に円弧出現
20190628102545.gif

#0から+1へ
library("animation")
Time_Code=c(exp(0),exp(0.1),exp(0.2),exp(0.3),exp(0.4),exp(0.5),exp(0.6),exp(0.7),exp(0.8),exp(0.9),exp(1.0))
saveGIF({
for (i in Time_Code){
　　root_move_01(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

それでは根が1/e以下だったり、e以上だったりするとどうなるのでしょう。なんとネイピア数周期で円を重ね書きし続けるのです。

根がe以上
20190628103123.gif

#+1から+2へ
library("animation")
Time_Code=c(exp(1.0),exp(1.1),exp(1.2),exp(1.3),exp(1.4),exp(1.5),exp(1.6),exp(1.7),exp(1.8),exp(1.9),exp(2.0))
saveGIF({
for (i in Time_Code){
　　root_move_01(i)
}
}, interval = 0.1, movie.name = "TEST.gif")  

image.gif

#+1から+6へ
library("animation")
Time_Code=c(exp(1.0),exp(1.5),exp(2.0),exp(2.5),exp(3.0),exp(3.5),exp(4.0),exp(4.5),exp(5.0),exp(5.5),exp(6.0))
saveGIF({
for (i in Time_Code){
　　root_move_01(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

根が1/e以下
20190628103446.gif

#-1から-2へ
library("animation")
Time_Code=c(exp(-1.0),exp(-1.1),exp(-1.2),exp(-1.3),exp(-1.4),exp(-1.5),exp(-1.6),exp(-1.7),exp(-1.8),exp(-1.9),exp(-2.0))
saveGIF({
for (i in Time_Code){
　　root_move_01(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

②①の符号を逆転させた自然指数関数-e^Xiあるいは-1/e^Xi

#統計言語Rによる実演例「-1/e^Xiと-e^Xiの狭間」
root_move_02<-function(rp){

#タイトル定義
Main_title<-c("Alternative to root")
x_title<-c("Real Expanse")
y_title<-c("Imaginaly Expanse")
#関数定義
f1<-function(x){rp^(x*(0+1i))} 
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
f2<-function(x){-rp^(x*(0+1i))} 
Circle_x=Im(f2(theta))
Circle_y=Re(f2(theta))
#f3<-function(x){log(x*(0+1i))}
cnv_y <- c(seq(-3, 3, length=300))
Log_plus <- f1(cnv_y)
#f4<-function(x){-log(x*(0+1i))} 
Log_minus <-f2(cnv_y) 
#f5<-function(x){2*x^2} 
#f6<-function(x){x^2} 
#f7<-function(x){4*x+5} 
#凡例用関数名定義
f1_name<-c("-root^xi(x=Real,y=Imaginaly),r=1") 
f2_name<-c("Exponential root^xi,-root^xi")  
f3_name<-c("Logarithmic log(xi, base=root),-log(xi, base=root)")  
#f4_name<-c("2*(x-3)^2") 
#f5_name<-c("2*x^2")  
#f6_name<-c("x^2") 

#グラフのスケール決定
gs_x<-c(-1.7,1.7)
gs_y<-c(-1.7,1.7)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#777777"
#グラフ描画
plot(Circle_x,Circle_y,xlim=gs_x,ylim=gs_y,type="l",col=Black, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(f1,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f2,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_plus, cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_minus,cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
#基準線
abline(h=0,,col=Gray)
abline(v=0,,col=Gray)
#塗りつぶし
polygon(c(Circle_x), #x
c(Circle_y), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　
#凡例描画
legend("bottomleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Black,Blue,Green))
}

根を-1(1/root)から0(root/root)にかけて変化させる->上から下に円弧消失
20190628111214.gif

#-1から0へ
library("animation")
Time_Code=c(exp(-1.0),exp(-0.9),exp(-0.8),exp(-0.7),exp(-0.6),exp(-0.5),exp(-0.4),exp(-0.3),exp(-0.2),exp(-0.1),exp(0.0))
saveGIF({
for (i in Time_Code){
　　root_move_02(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

根を0(root/root)から1(root)にかけて変化させる->下から上に円弧出現
20190628111345.gif

#0から+1へ
library("animation")
Time_Code=c(exp(0),exp(0.1),exp(0.2),exp(0.3),exp(0.4),exp(0.5),exp(0.6),exp(0.7),exp(0.8),exp(0.9),exp(1.0))
saveGIF({
for (i in Time_Code){
　　root_move_02(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

③自然対数関数log(Xi)あるいはlog(Xi,base=1/exp(1))

#統計言語Rによる実演例「log(Xi)とlog(Xi,base=1/exp(1)の狭間」

root_move_03<-function(rp){

#タイトル定義
Main_title<-c("Alternative to root")
x_title<-c("Real Expanse")
y_title<-c("Imaginaly Expanse")
#関数定義
f1<-function(x){rp^(x*(0+1i))} 
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
Circle_y=Im(f1(theta))
Circle_x=Re(f1(theta))

f2<-function(x){-rp^(x*(0+1i))} 
#f3<-function(x){log(x*(0+1i))}
cnv_y <- c(seq(-3, 3, length=300))
Log_plus <- f1(cnv_y)
#f4<-function(x){-log(x*(0+1i))} 
Log_minus <-f2(cnv_y) 
#f5<-function(x){2*x^2} 
#f6<-function(x){x^2} 
#f7<-function(x){4*x+5} 
#凡例用関数名定義
f1_name<-c("log(xi)(x=Real,y=Imaginaly),r=1") 
f2_name<-c("Exponential root^xi,-root^xi")  
f3_name<-c("Logarithmic log(xi, base=root),-log(xi, base=root)")  
#f4_name<-c("2*(x-3)^2") 
#f5_name<-c("2*x^2")  
#f6_name<-c("x^2") 

#グラフのスケール決定
gs_x<-c(-1.7,1.7)
gs_y<-c(-1.7,1.7)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#777777"
#グラフ描画
plot(Circle_x,Circle_y,xlim=gs_x,ylim=gs_y,type="l",col=Black, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(f1,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f2,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_plus, cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_minus,cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
#基準線
abline(h=0,,col=Gray)
abline(v=0,,col=Gray)
#塗りつぶし
polygon(c(Circle_x), #x
c(Circle_y), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　
#凡例描画
legend("bottomleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Black,Blue,Green))
}

根を-1(1/root)から0(root/root)にかけて変化させる->左から右に円弧消失
20190628110120.gif

#-1から0へ

library("animation")
Time_Code=c(exp(-1.0),exp(-0.9),exp(-0.8),exp(-0.7),exp(-0.6),exp(-0.5),exp(-0.4),exp(-0.3),exp(-0.2),exp(-0.1),exp(0.0))
saveGIF({
for (i in Time_Code){
　　root_move_03(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

根を0(root/root)から1(root)にかけて変化させる->右から左に円弧出現
20190628110257.gif

#0から+1へ
library("animation")
Time_Code=c(exp(0),exp(0.1),exp(0.2),exp(0.3),exp(0.4),exp(0.5),exp(0.6),exp(0.7),exp(0.8),exp(0.9),exp(1.0))
saveGIF({
for (i in Time_Code){
　　root_move_03(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

④③の符号を逆転させた自然対数関数-log(Xi)あるいは-log(Xi,base=1/exp(1))

#統計言語Rによる実演例「-log(Xi)と-log(Xi,base=1/exp(1)の狭間」

root_move_04<-function(rp){

#タイトル定義
Main_title<-c("Alternative to root")
x_title<-c("Real Expanse")
y_title<-c("Imaginaly Expanse")
#関数定義
f1<-function(x){rp^(x*(0+1i))} 
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
f2<-function(x){-rp^(x*(0+1i))} 
Circle_y=Im(f2(theta))
Circle_x=Re(f2(theta))
#f3<-function(x){log(x*(0+1i))}
cnv_y <- c(seq(-3, 3, length=300))
Log_plus <- f1(cnv_y)
#f4<-function(x){-log(x*(0+1i))} 
Log_minus <-f2(cnv_y) 
#f5<-function(x){2*x^2} 
#f6<-function(x){x^2} 
#f7<-function(x){4*x+5} 
#凡例用関数名定義
f1_name<-c("log(xi)(x=Real,y=Imaginaly),r=1") 
f2_name<-c("Exponential root^xi,-root^xi")  
f3_name<-c("Logarithmic log(xi, base=root),-log(xi, base=root)")  
#f4_name<-c("2*(x-3)^2") 
#f5_name<-c("2*x^2")  
#f6_name<-c("x^2") 

#グラフのスケール決定
gs_x<-c(-1.7,1.7)
gs_y<-c(-1.7,1.7)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#777777"
#グラフ描画
plot(Circle_x,Circle_y,xlim=gs_x,ylim=gs_y,type="l",col=Black, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(f1,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f2,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_plus, cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(Log_minus,cnv_y,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
#基準線
abline(h=0,,col=Gray)
abline(v=0,,col=Gray)
#塗りつぶし
polygon(c(Circle_x), #x
c(Circle_y), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　
#凡例描画
legend("bottomleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Black,Blue,Green))
}

根を-1(1/root)から0(root/root)にかけて変化させる->右から左に円弧消失
20190628110800.gif


#-1から0へ
library("animation")
Time_Code=c(exp(-1.0),exp(-0.9),exp(-0.8),exp(-0.7),exp(-0.6),exp(-0.5),exp(-0.4),exp(-0.3),exp(-0.2),exp(-0.1),exp(0.0))
saveGIF({
for (i in Time_Code){
　　root_move_04(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

根を0(root/root)から1(root)にかけて変化させる->左から右に円弧出現
20190628110918.gif

#0から+1へ
library("animation")
Time_Code=c(exp(0),exp(0.1),exp(0.2),exp(0.3),exp(0.4),exp(0.5),exp(0.6),exp(0.7),exp(0.8),exp(0.9),exp(1.0))
saveGIF({
for (i in Time_Code){
　　root_move_04(i)
}
}, interval = 0.1, movie.name = "TEST.gif") 

詳しい数理的背景の説明は以下にお任せしましょう。私自身はこんなに上手く説明出来ません。
何なんだろうな。あいじょうって。「10のi乗」みたいな数を考える
iのi乗はそこに至る経路で決まる
実際に自分でプログラミングして実感したのが「平方眼(Square Grid)が歪んでいく異様な感じ」。さて、この概念(Concept)は何処へと繋がっていくのでしょう？

1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1