- (2021年3月13日)初投稿
- (2021年4月19日)等速円運動と複素平面の概念的統合
等速円運動(Constant Velocity Circular Motion)についての物理学上の説明は向心加速度(Centripetal Acceleration)成分を外部化する事で、数学上の説明はオイラーの公式$e^{θi}=\cos(θ)+\sin(θ)i$から出発する事で随分と単純化されています。まずはその事実の確認…
#等速円運動(Constant Velocity Circular Motion)とは？
円運動（circular motion） - Wikipedia
回転運動を回転面上の観測者が真横から見ると物体は単振動(Simple Vibration)しているように見える。あるいは物体のｘ座標とｙ座標が互いに位相が90度=π/２ずれた単振動を行っている様に見える。
かかる単振動運動(Simple Vibration Motion)においては回転速度=角速度(Angular Velocity)rad/sのことを周波数/振動数(Frequency)Hzとも呼ぶ。
単振動SV(Simple Vibration)を物理学の世界で標準採用されている時間軸t($t=0 \to \infty$)に置くと以下の様に見えます。
SV_x(0→1→2→3→4→…)=(1→0→-1→1→0→…)\\
SV_y(0→1→2→3→4→…)=(0→1→0→-1→0→…)
そう「位相が90度($\frac{π}{2}$)ずれている」は、まずこう見えるのです。ある意味交代級数(Alternating Series)$-1^n=(…-1,1,-1,1,…)$概念のさらなる拡張といえましょう。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数
-1^n=(…-1,1,-1,1,…)\\
-1=i^2=(0 \pm 1i)^2\\
\therefore-1^n=i^{2n}=(0 \pm 1i)^{2n}
- 概ね単位周期(Unit Cycle)と周回数(Number of Laps)の両方を見る場合には角速度rad/s表示、周回数のみを見る場合には周回数Hz表示が採用される。
とりあえずこの観測結果集合(Observation Result Set)が(x軸からの観測結果に由来する)余弦波（Cosin wave）と(y軸からの観測結果に由来する)正弦波(Sine wave）の正体という訳です。そして物理学の世界と数学の世界それぞれに、これに対応する独自の演算結果集合(Operation Result Set)の導出方法が存在するのです。
##物理学の場合
等速円運動から向心加速度(Centripetal Acceleration)成分を抽出し、残りを(円軌道上の)等速直線運動として捉えます。その過程で上掲の観察結果集合としての$\cos(θ),\sin(θ)$を使いますが、それらの演算結果集合としての規定までは手掛けません(そちらは数学任せ?)。
等速円運動 ： 位置 (pisition)，速度 (velocity)，加速度 (acceleration)
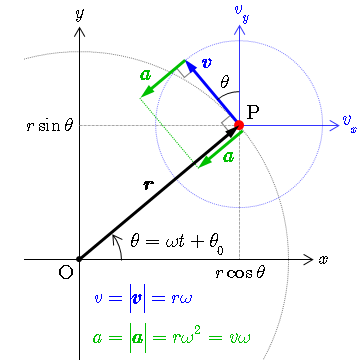
まず等速円運動の中心が原点Oの場合を考える。
原点Oを中心とした半径rの円周上を角速度ωで等速円運動する質点の位置r=(x,y)の各成分はと表される（$θ_0$：初期位相）
x(t)=r\cos(ωt+θ_0)…式(1)\\
y(t)=r\sin(ωt+θ_0)…式(2)
質点の速度$v=\frac{dr}{dt}=(v_x,v_y)$の各成分は以下となる。
v_x(t)=\frac{dx}{dt}=−ωr\sin(ωt+θ_0)…式(3)\\
v_y(t)=\frac{dy}{dt}=ωr\cos(ωt+θ_0)…式(4)
ここで位置ベクトル$\vec{r}$と速度ベクトル$\vec{v}$の内積(Inner Product)を求めると0となり、速度ベクトル$\vec{v}$が位置ベクトル$\vec{r}$（動径方向）と直交している事が分かる(ユークリッド幾何学でいう「円の中心から弦に引いた垂線は全て弦の中点を通る垂直二等分線となる」定理に対応)。
r⋅v=r\cos(ωt+θ_0)(−rω\sin(ωt+θ0))+r\sin(ωt+θ_0)rω\cos(ωt+θ_0)\\
=−r2ω\sin(ωt+θ_0)\cos(ωt+θ_0)+r2ω\sin(ωt+θ_0)\cos(ωt+θ_0)\\
=0
速度ベクトル$\vec{v}$は接線方向を向いており、その大きさは以下となる。
v=\sqrt{v^2_x+v^2_y}\\
=\sqrt{ω^2r^2\sin^2(ωt+θ_0)+ω^2r^2cos^2(ωt+θ_0)}\\
=\sqrt{r^2ω^2}\\
=rω…式(5)
- 通常，回転方向は反時計回りのみを考えてω>0で考えるが，時計回りの回転も考慮するとω<0の場合もありえるので，その場合この式(5)で現れるrωについて絶対値|ω|で置き換える必要がある。
この時、質点の加速度a=dv/dt=(ax,ay)の各成分は以下となる。
a_x(t)=\frac{dvx}{dt}=−ω^2r\cos(ωt+θ_0)\\
=−ω2x…式(6)\\
a_y(t)=\frac{dvy}{dt}=−ω^2r\sin(ωt+θ_0)\\
=−ω2y…式(7)
上の2式より加速度aはこう定義される。
a=−ω^2r…式(8)
この加速度aは位置rと逆向きで，常に円の中心Oを向いていることから 向心加速度(Centripetal Acceleration) と呼ばれ、その大きさは以下の様に定義される。
a=|a|=∣−ω^2r∣=rω^2=vω=\frac{v^2}{r}…式(9)
- 通常，回転方向は反時計回りのみを考えてω>0で考えるが，時計回りの回転も考慮するとω<0の場合もありえるので，その場合この式(9)で現れるvωについて絶対値|ω|で置き換える必要がある。
図から分かるように，質点の位置を原点とした速度空間（$v_{x}v_{y}$平面）で考えると，vは，半径vの円周上を速さvωで等速円運動していると考えることができる。
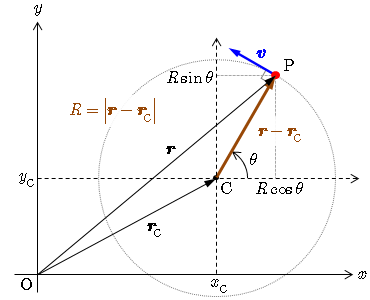
等速円運動の中心を原点Oではなく任意の点に一般化する。
等速円運動の中心を原点Oではなく任意の点 C($x_C,y_C$)とすると，位置ベクトル$\vec{r}$の各成分を表す式(1)，式(2)は、以下の式(10),式(11)で置き換えられる（ここで，円周の半径をRとした）。
x(t)=R\cos(ωt+θ_0)+x_C…式(10)\\
y(t)=R\sin(ωt+θ_0)+y_C…式(11)
xCとyCは定数であるので，速度vと加速度aの式は変わらない．この場合，点Cの位置ベクトルを$r_C=(x_C,y_C)$とすると，式(8)は式(12)の形に書き換えられる。
a=−ω^2(r−r_C)…式(12)
この場合も加速度は常に中心Cを向いていることになるので，向心加速度には変わりない。
##数学の場合
演算結果集合としての円描画関数$e^{θi}=\cos(θ)+\sin(θ)i$から出発する。
###無限連続高階微積分による位相推移。
数学の世界は$\sin(θ)$波と$\cos(θ)$波が同じ波形の位相を時間的にシフトさせたものに過ぎない事を無限連続高階微積分(Infinite calculus)によって説明する。
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」？
三角関数の積分（それぞれが-90度の変遷に対応）
\int \int \int … \int \cos(θ)(dθ)=(\sin(θ),-\cos(θ),-\sin(θ),\cos(θ),…)\\
\int \int \int … \int \sin(θ)(dθ)=(-\cos(θ),-\sin(θ),\cos(θ),\sin(θ),…)
円描画関数$e^{θi}=\cos(θ)+\sin(θ)$の微分（それぞれが+90度の変遷に対応）
(\cos(θ)+\sin(θ)i)\frac{d^n}{dθ^n}=(-\sin(θ)+\cos(θ)i,-(\cos(θ)+\sin(θ)i),-(-\sin(θ)+\cos(θ)i),\cos(θ)+\sin(θ)i,…)\\
e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log θi),-e^{ix},-i e^{i x}(\log θi),e^{ix},…)
円描画関数$e^{θi}=\cos(θ)+\sin(θ)$の積分（それぞれが-90度の変遷に対応）
\int \int \int … \int (\cos(θ)+\sin(θ)i)(dθ)=(-(-\sin(θ)+\cos(θ)i),-(\cos(θ)+\sin(θ)i),-\sin(θ)+\cos(θ)i,\cos(θ)+\sin(θ)i,…)\\
\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log θi),- e^{i x},i e^{i x}(-\log θi),e^{ix},…)
すなわち微積分概念の導入により、$θ_n(n=1→-1)=(0,…,\frac{π}{2},…,π)$と置いた場合の円描画関数$e^{θi}=\cos(θ)+\sin(θ)i$は以下の8位相に拡張される。
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」？
元関数=4階微分/4階積分(最初に戻る)
e^{θ_ni}=\cos（θ)+\sin（θ)i…(θ_0=0)
$i=(0+1i)$と置いた場合
$i=(0-1i)$と置いた場合
1階微分/3階積分
\log θ_ni=-i e^{θ_ni}=-(-\sin（θ_n)+\cos（θ_n)i)…(θ_0=\frac{π}{2})
$i=(0+1i)$と置いた場合
$i=(0-1i)$と置いた場合
2階微分/2階積分
-e^{θ_ni}=-(\cos（θ_n)+\sin（θ_n)i)…(θ_0=π)
$i=(0-1i)$と置いた場合
$i=(0+1i)$と置いた場合
3階微分/1階積分
-\log θ_ni=i e^{θ_ni}=-\sin（θ_n)+\cos（θ_n)i…(θ_0=-\frac{π}{2})
$i=(0-1i)$と置いた場合
$i=(0+1i)$と置いた場合
- 上掲の様に無限に1を返し続ける周回級数(Lap Series)$1^n=(…1,1,1,1,…)$概念を拡張したのが交代級数(Alternating Series)$-1^n=(…-1,1,-1,1,…)$概念で、それをさらに拡張したのがこの複素級数(Complex Series)$i^{2n}=(…1,i^{2n+1},i^{2n}=-1,-i^{2n+1},-i^{2n}=1,…)$概念とも考えられるが、実は多価関数である為、この段階では「1階微分する=90度($\frac{π}{2}$)シフトさせる」操作と「3階積分する=-270度($-\frac{3π}{2}$)シフトさせる」操作、および「3階微分する=270度($\frac{3π}{2}$)シフトさせる」操作と「1階積分する=-90度($-\frac{π}{2}$)シフトさせる」操作を区別する方法が本質的に存在しない。複素解析学(Complex Analysis)はこれに分枝点(Branch Point)概念や分岐截断(Branch Cut)概念を導入する事で実数空間同様に微積分可能な演算空間を整備した。
分岐点(数学) - Wikipedia
【数理考古学】とある実数列(Real Sequance)の規定例①等差数列から加法整数群へ
またこの概念は微積分がフーリエ変換/逆変換(Fourier Transform(FT)/Inverse Transform)において回転角度の乗除算、ラプラス変換/逆変換(Laplace Transform/Inverse Transform)において位相の加減算に置換される考え方の出発点でもある。
【数理考古学】とある実数列(Real Sequance)の規定例④フーリエ族(Fourier Family)とラプラス族(Laplace Family)概念の追加? - さらには階乗の概念を複素数全体に拡張したΓ関数は$i^2=-1$を原義とする虚数iが$\pm i=e^{\frac{\pm iπ}{2}}$および$ie^2=e^{2+\frac{iπ}{2}}$となり、上掲の様に複素級数が偶奇性(2nと2n+1の交代的出現)を備える事から構想された特殊関数である。
log(-i)って？？底はe
複素数の対数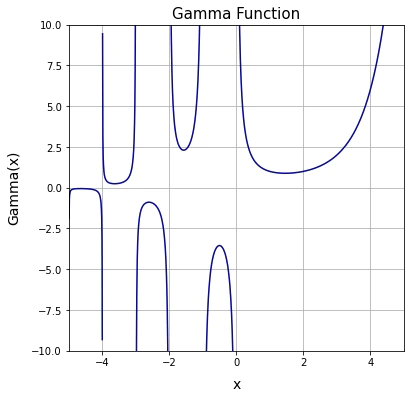
かくして数学の世界はかかるΓ関数の概念導入によって「半径と直径、円の周長と面積、球の表面積と体積の数理」の統合を果たす。
【Python演算処理】階乗と順列と組み合わせ
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」？
###三角関数概念の導出
高校数学でわかる複素関数 微分からコーシー積分、留数定理まで (ブルーバックス) | 竹内淳 | 数学 | Kindleストア | Amazon
①オイラーの公式を用いるとコサイン波$\cos(θ)$とサイン波$\sin(θ)$を$e^{θi}$と$e^{-θi}$で表せます。
e^{θi}=\cos(θ)+\sin(θ)i(2-0)\\
e^{-θi}=\cos(-θ)+\sin(-θ)i=\cos(-θ)-\sin(θ)i…(2-1)
②コサイン波$\cos(θ)$の場合は…
e^{θi}+e^{-θi}=2\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}…(2-2)
③サイン波の場合は(2-0)式より(2-1)式を引いて2iで割ります。
\frac{e^{θi}-e^{-θi}}{2i}…(2-3)
④複素数の極形式も次の様に指数関数で表せます。
a+bi=r(\cos(θ)+\sin(θi))=re^{iθ}
⑤また複素共役は以下となります。
a-bi=r(cos(θ)-sin(θi))=re^{-iθ}
⑥ピタゴラスの定理はこう表されます。
cos(θ)^2+sin(θ)^2\\
=\frac{e^{2θ}+2(e^{iθ}×e^{-iθ})+e^{-2θ}}{4}-\frac{e^{2θ}-2(e^{iθ}×e^{-iθ})+e^{-2θ}}{4}\\
=\frac{4(e^{iθ}×e^{-iθ})}{4}=1
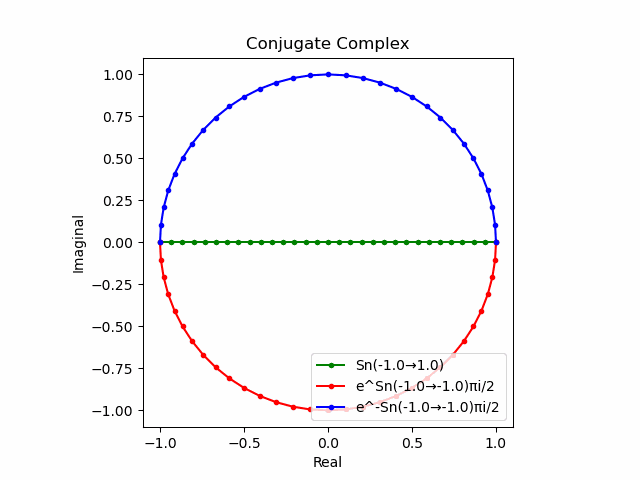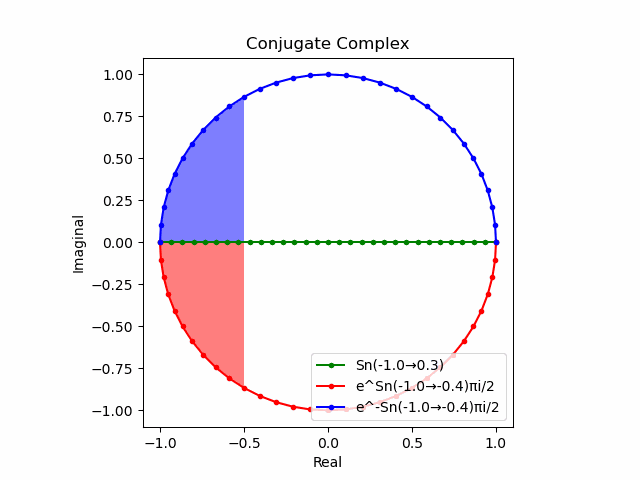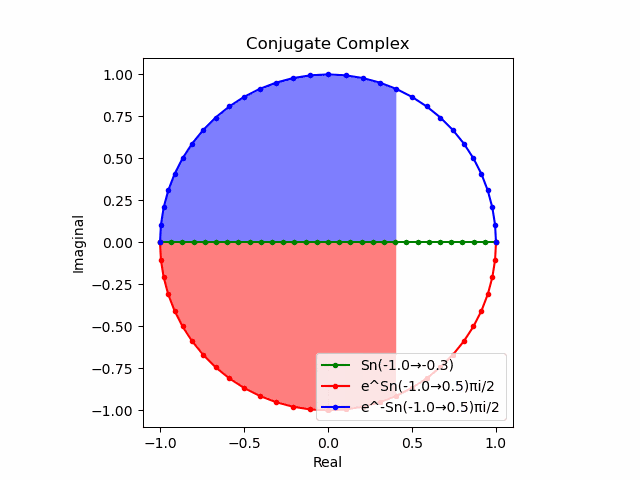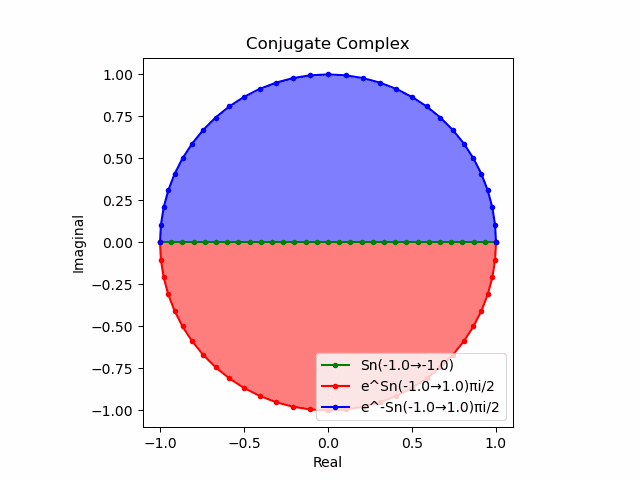
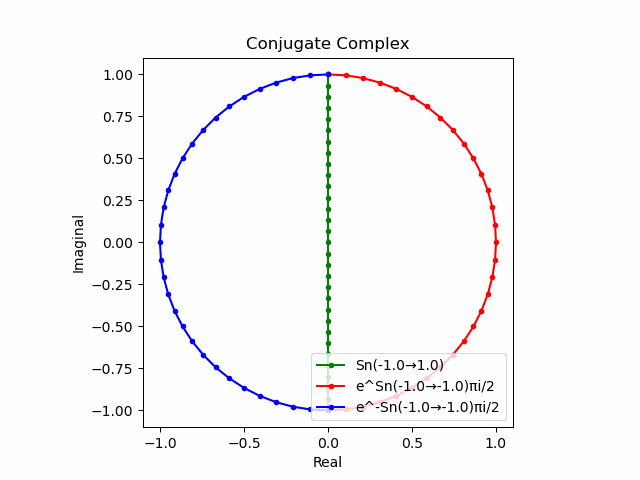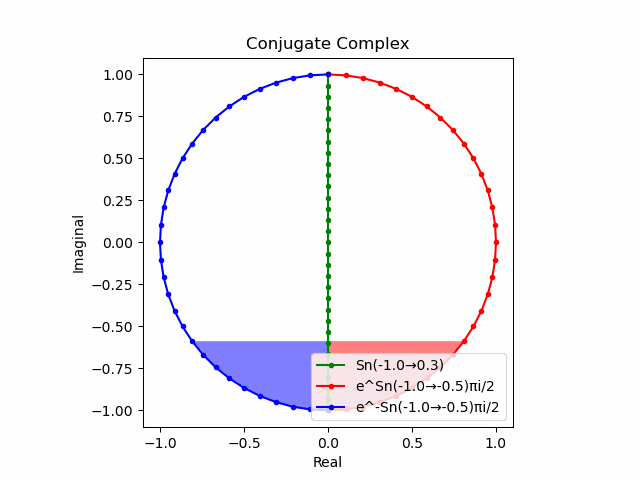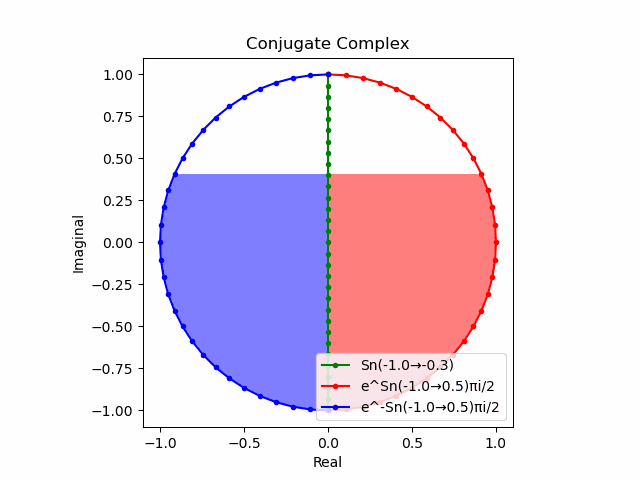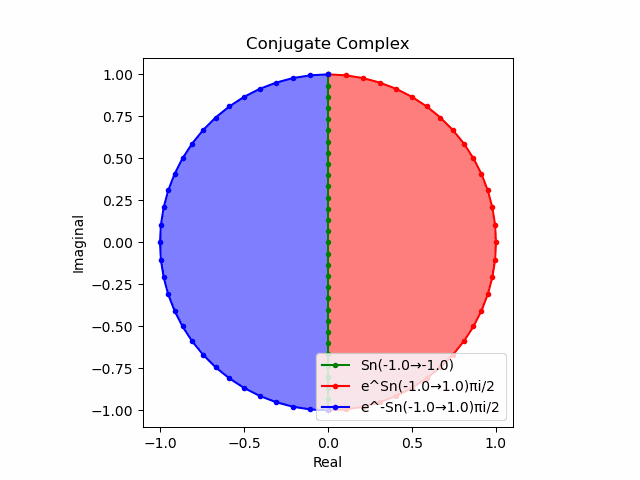
$θ_n(n=1→-1)=(0,…,\frac{π}{2},…,π)$と置いた場合、 $e^{θ_ni}$と$e^{-θ_ni}$が共役関係を構成する。$(n=1→-1)$の条件を満たすのは$θ_n*(0+1i)$の位相。
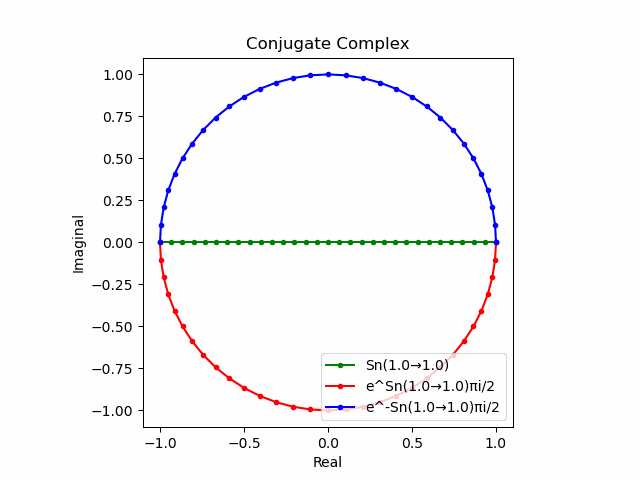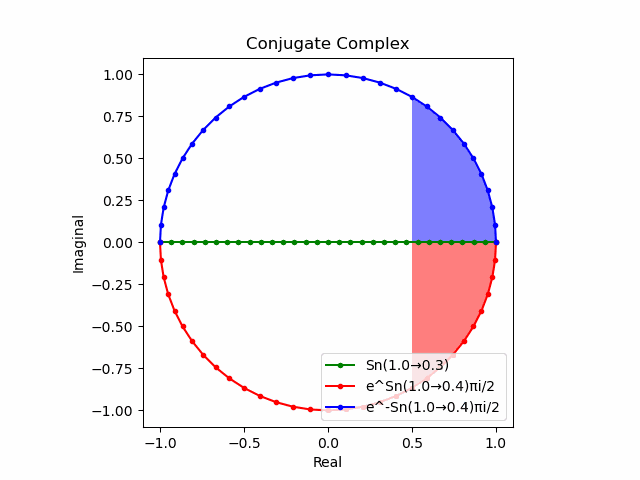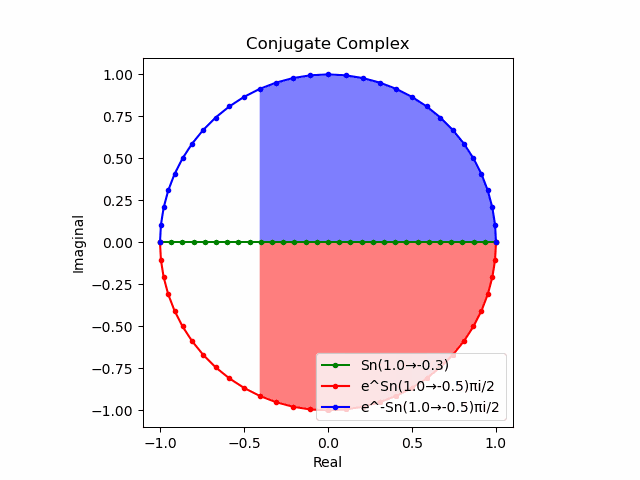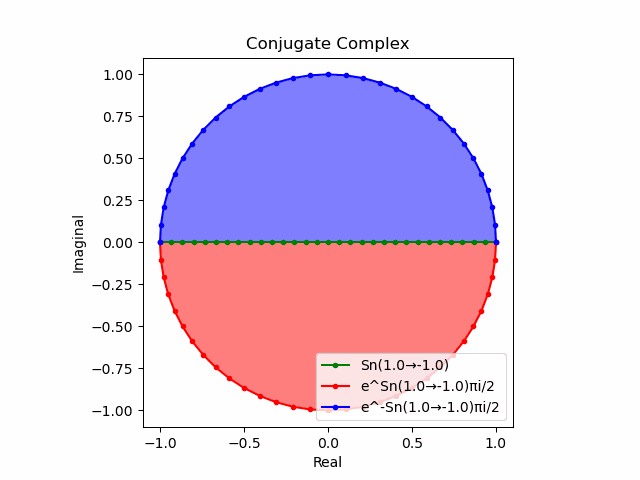
そして$e^{θ_ni}+e^{-θ_ni}$は幅2倍の横棒、$e^{θ_ni}-e^{-θ_ni}$は高さ2倍の縦棒となる。
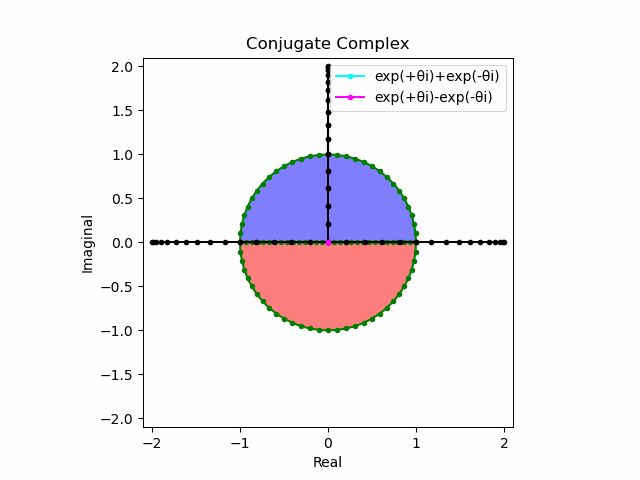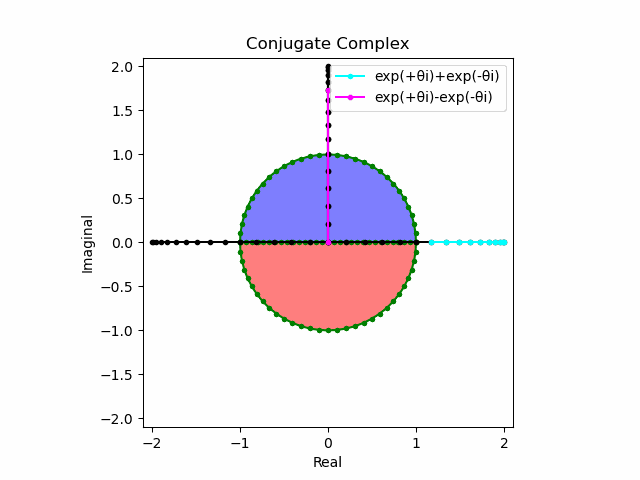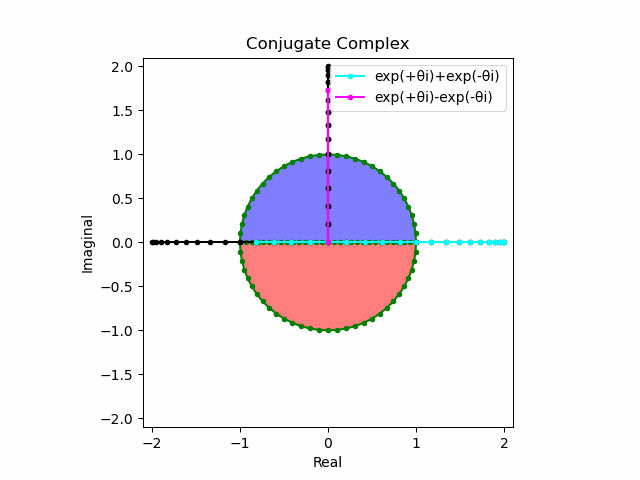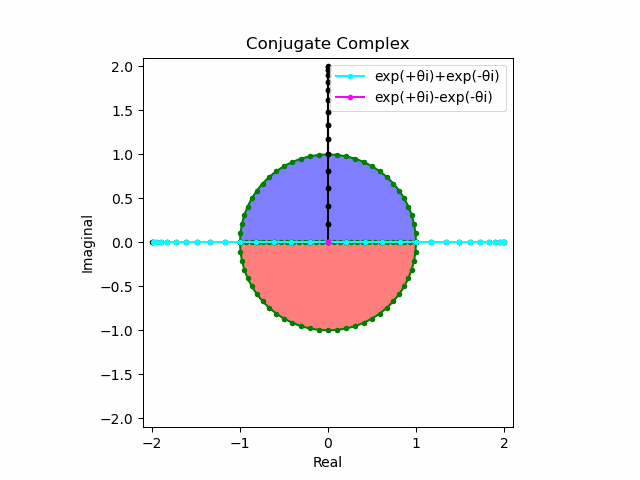
これを2で割って平均を求めると幅も高さも1に戻る。$\cos(θ)$の導出式は$\frac{e^{θ_ni}+e^{-θ_ni}}{2}$なのでこちらの答えはこの時点で得られる。
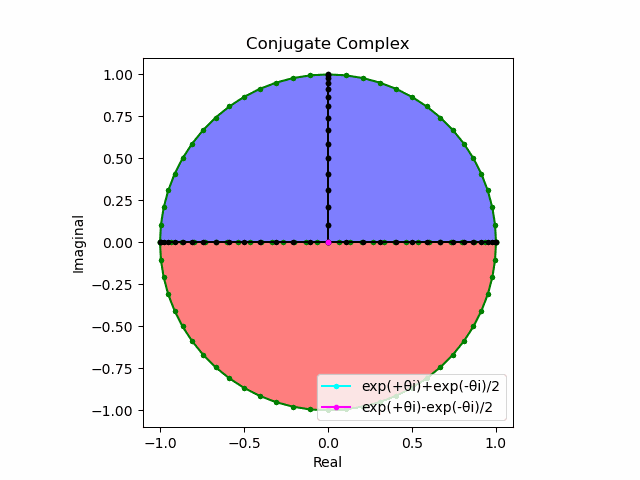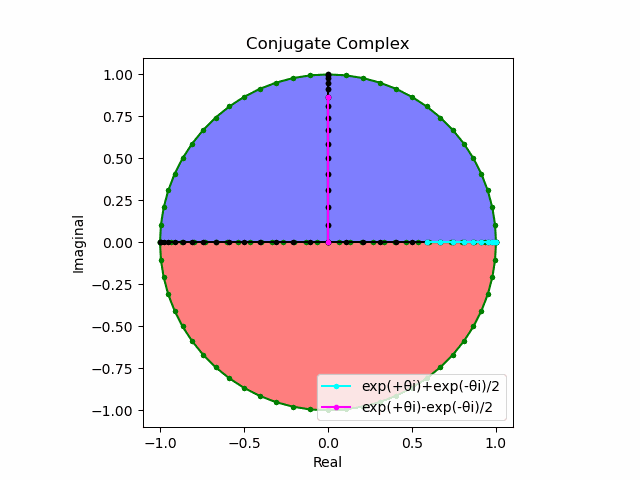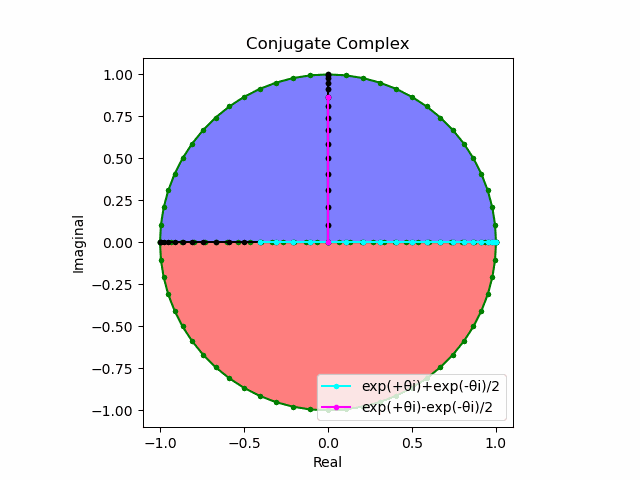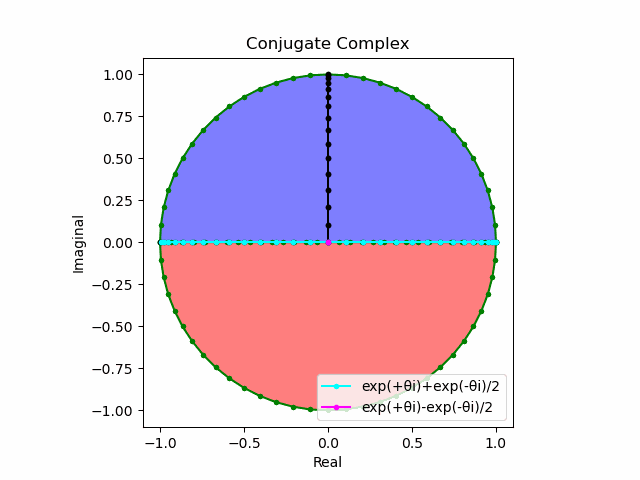
そしてさらにこれを+90度($+\frac{π}{2}$ラジアン)回転させた$\frac{e^{+θ_n πi}-e^{-θ_ni}}{2(0+1i)}$の結果が$\sin(0→π)$と一致する。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
#単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
#共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly1=(p1-m1)/2
ly2=(p1-m1)/(2*(0+1j))
u0=num.linspace(m.pi,0,31,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(m.sin(u0[nm]))
u2=num.array(u1)
print("Imaginal of $\frac{exp(+θ_n(0+1i))-exp(-θ_n(0+1i)))}{2}$=",num.round(ly1.imag,8))
print("Real of $\frac{exp(+θ_n(0+1i))-exp(-θ_n(0+1i))}{2*(0-1i)}=",num.round(ly2.real,8))
print("$\sin(0→π)$=",num.round(u2,8))
Imaginal of $\frac{exp(+θ_n(0+1i))-exp(-θ_n(0+1i)))}{2}$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
Real of $\frac{exp(+θ_n(0+1i))-exp(-θ_n(0+1i))}{2*(0+1i)}$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
$\sin(0→π)$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
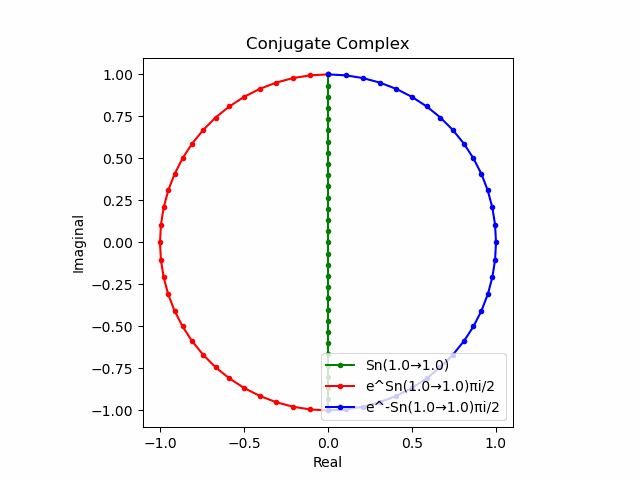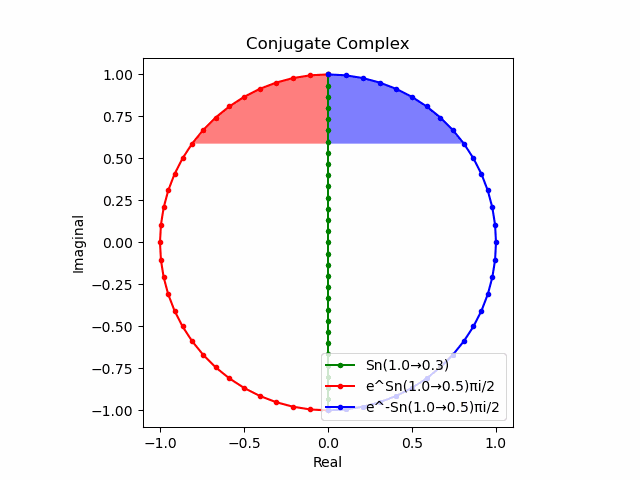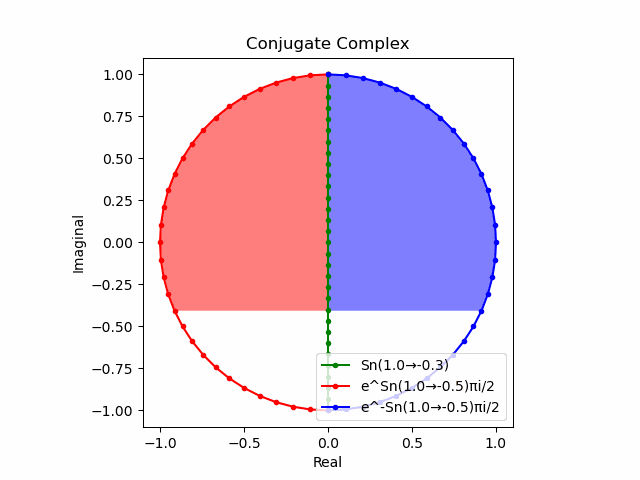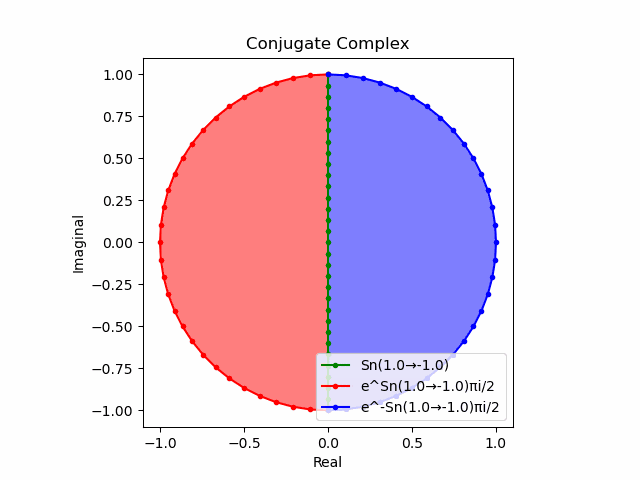
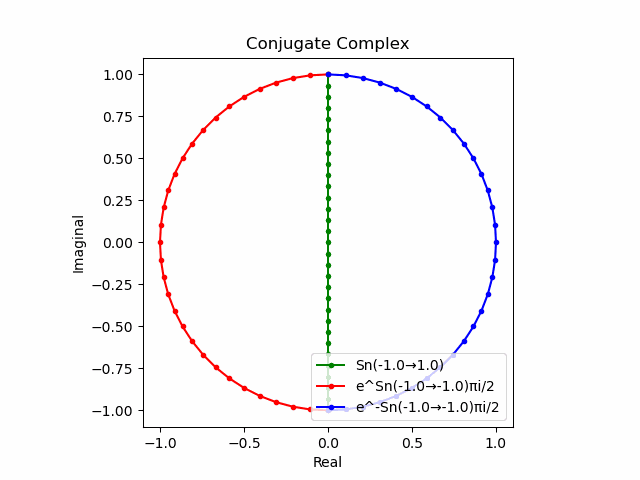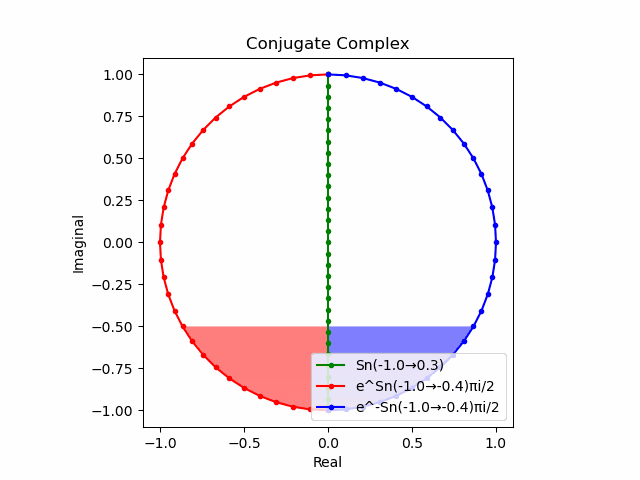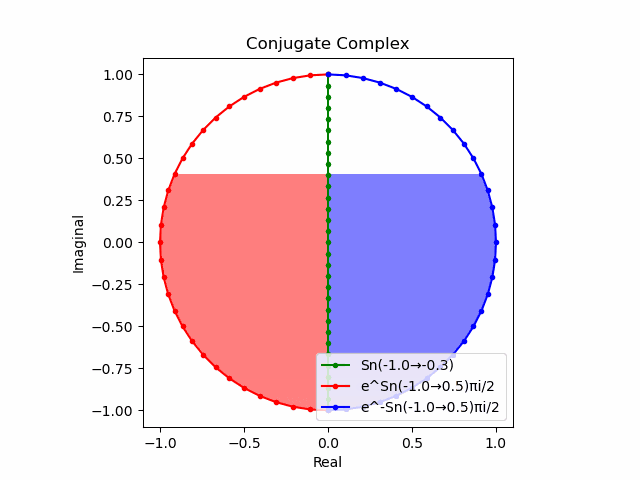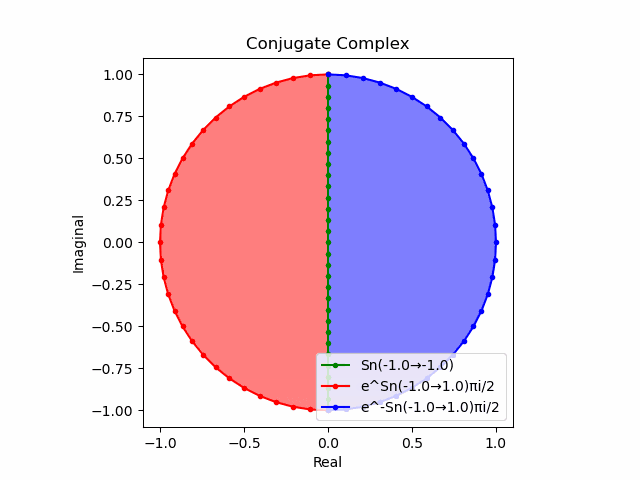
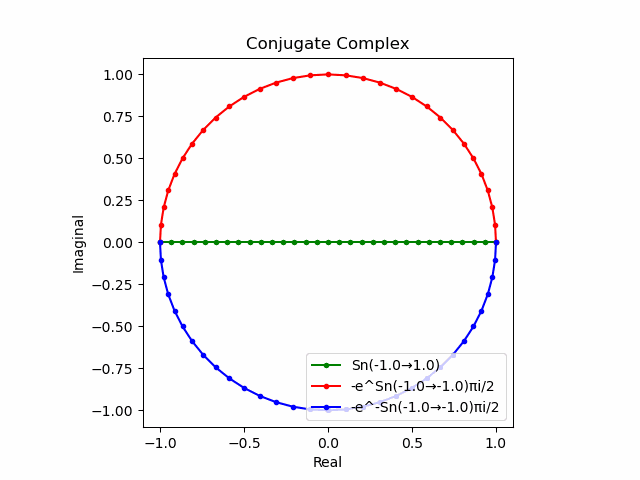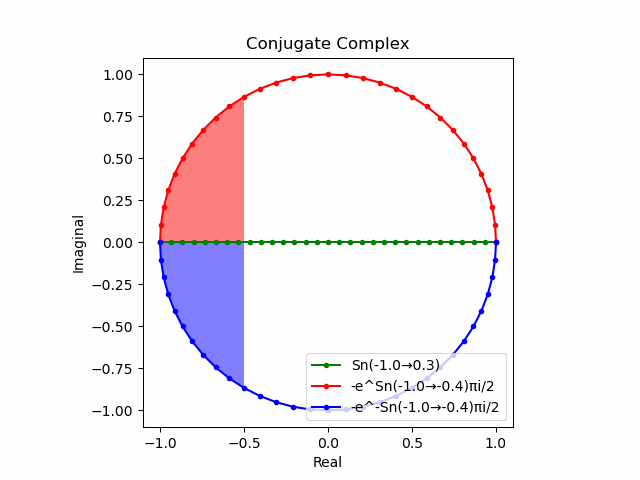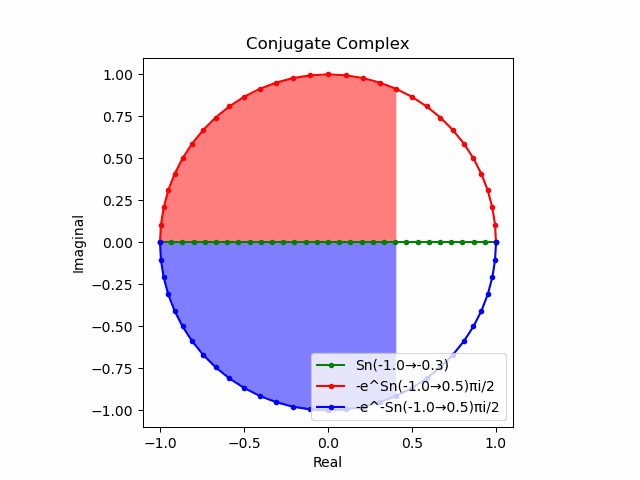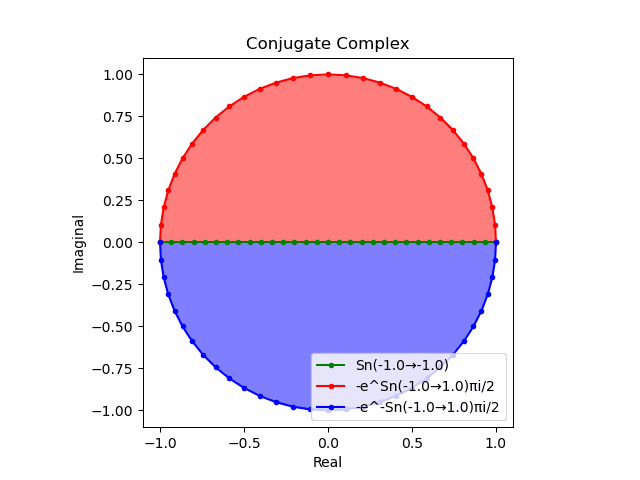
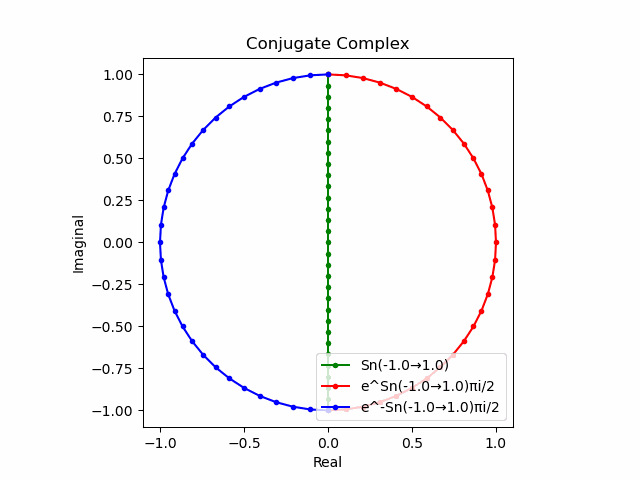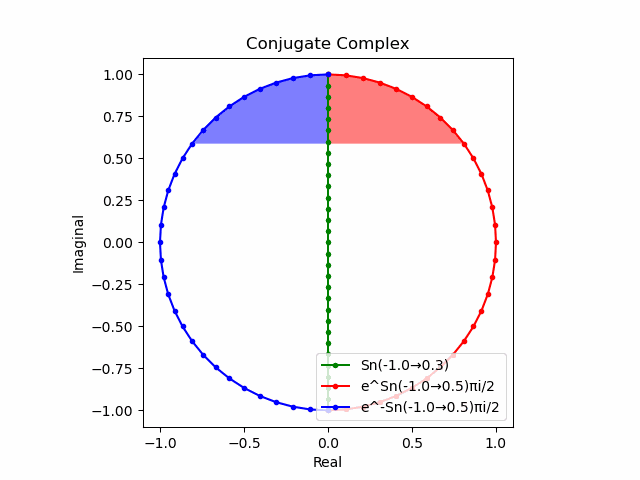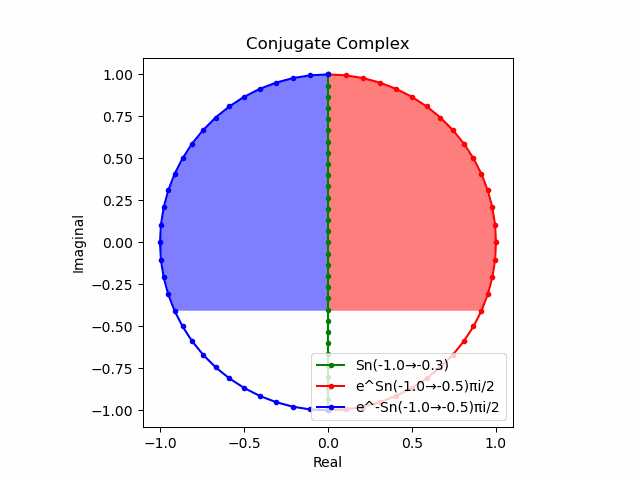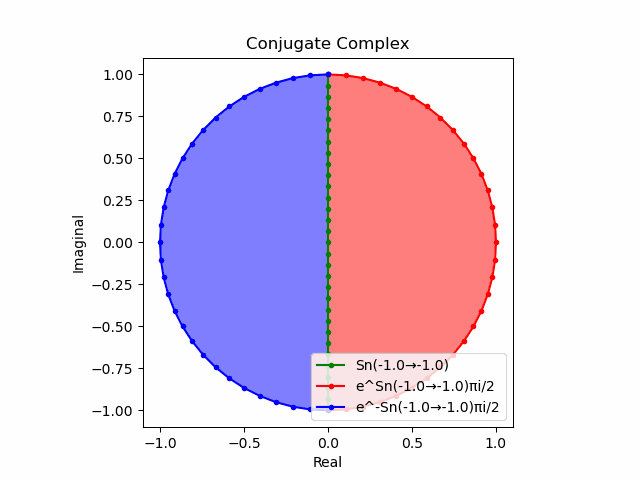
かかる共役関係は$-e^{θ_ni}$と$-e^{-θ_ni}$の場合も維持され、この場合$(n=1→-1)$の条件が継承されるのは$θ_n*(0+1i)$の位相となる。
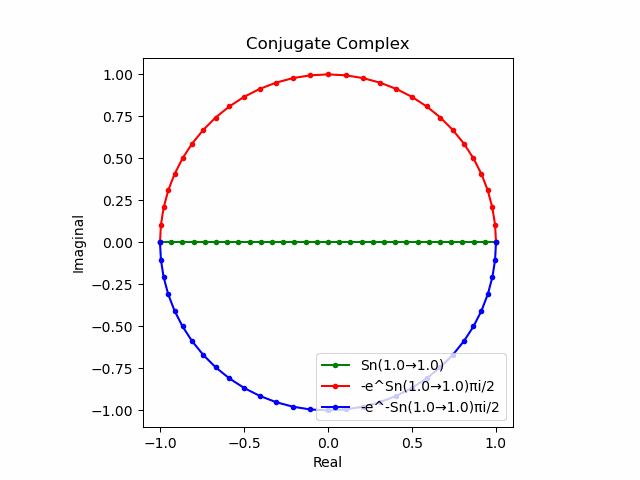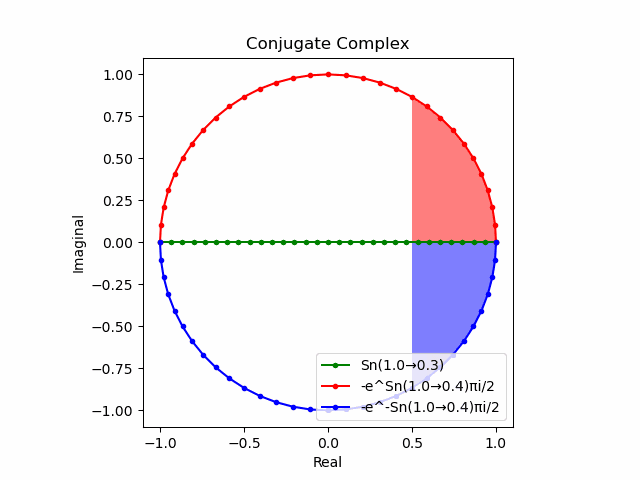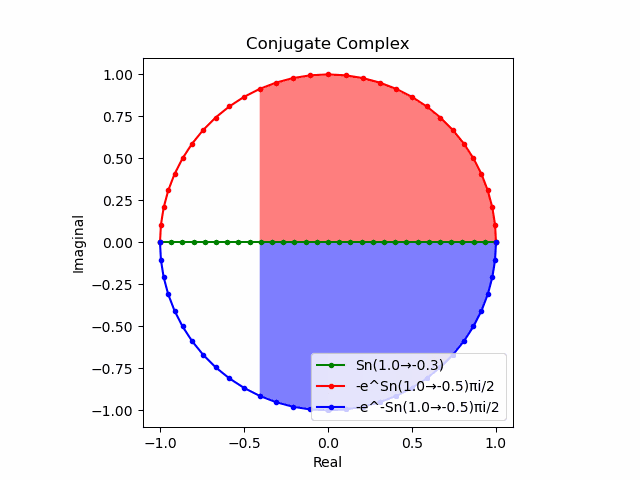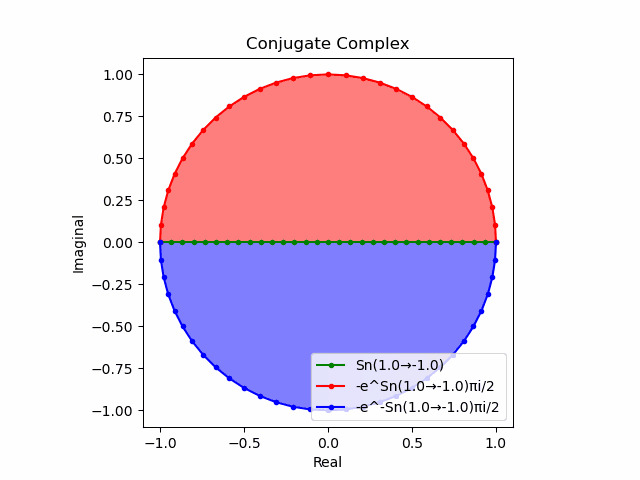
この場合ももちろん$-(e^{θ_ni}+e^{-θ_ni})$は幅2倍の横棒、$e^{-θ_ni}-e^{+θ_ni}$は高さ2倍の縦棒となる。
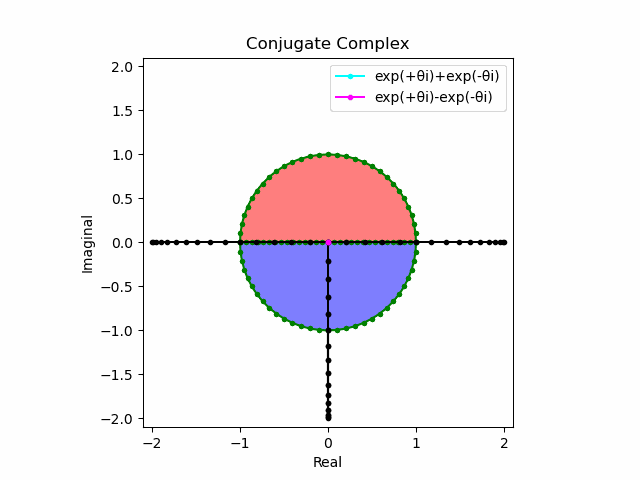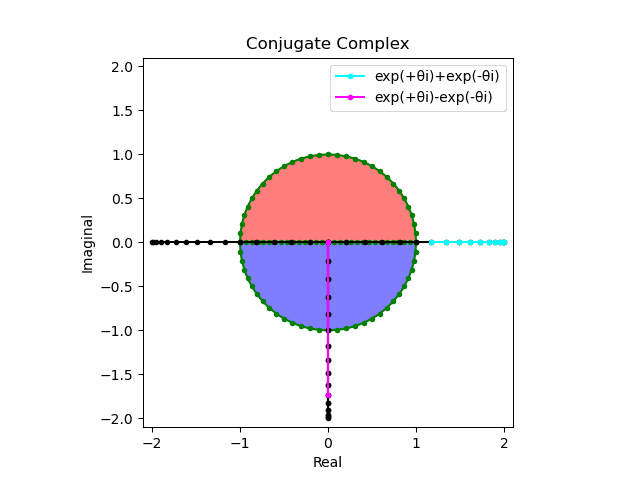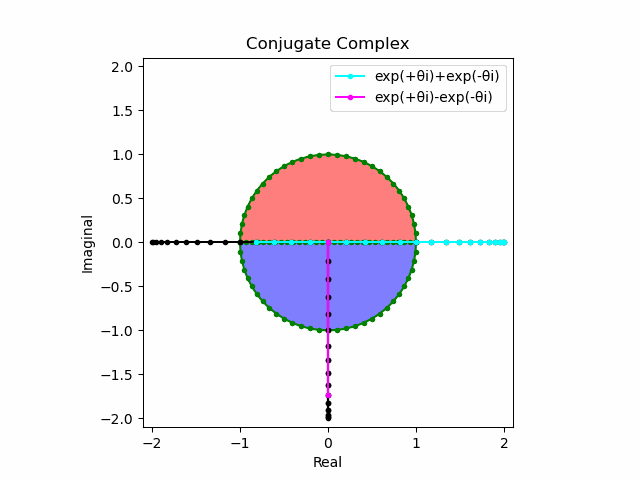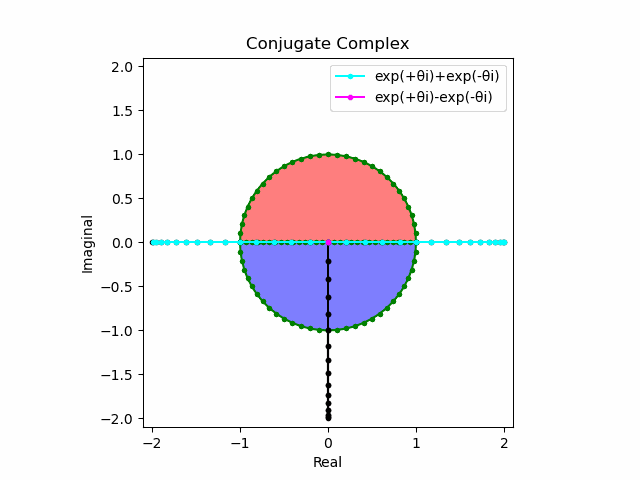
2で割って平均を求めた結果が幅も高さも1に戻るのも同じ。$\cos(θ)$の導出式は$\frac{e^{θ_ni}+e^{-θ_ni}}{2}$なのでこちらの答えはこの時点で得られる。符号が逆だが結果は同じ。そう、$\cos(θ)$は「回転の方向がない(逆関数を備えない)」偶関数なのである。
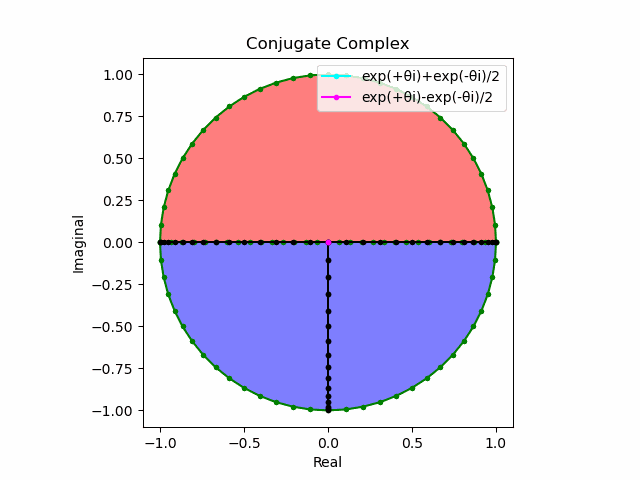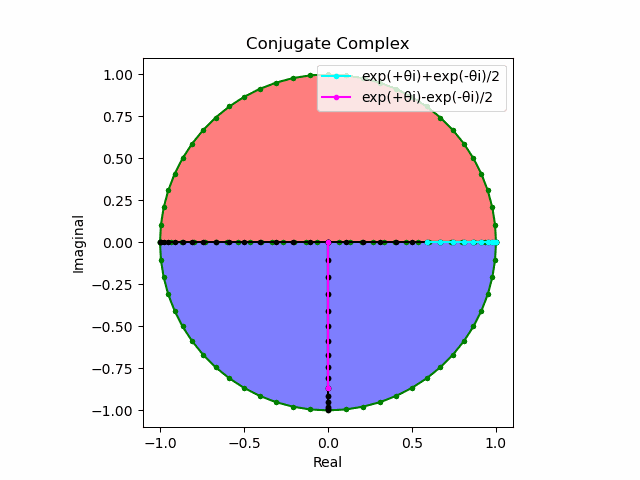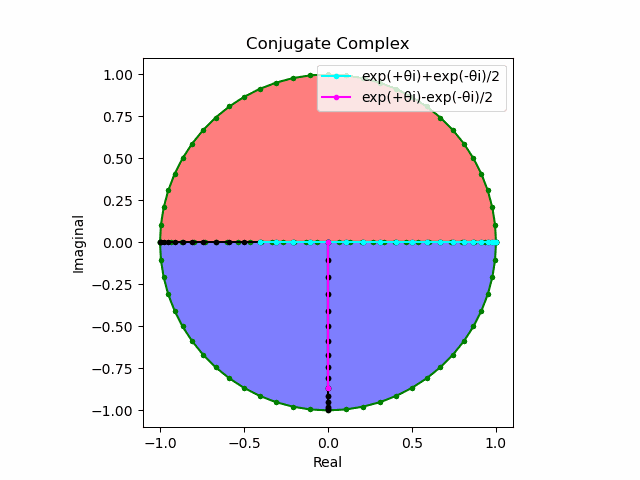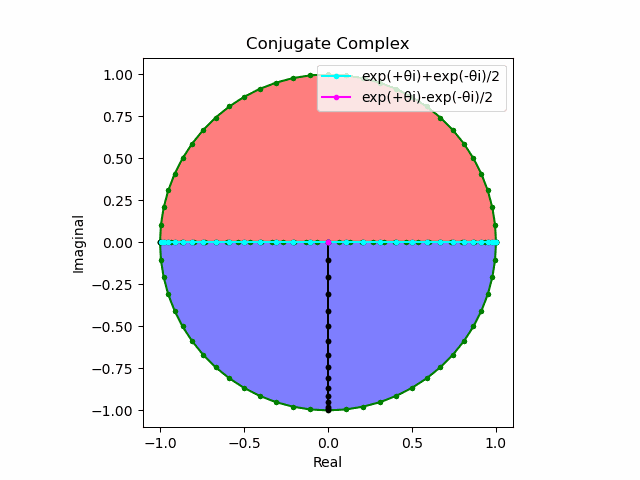
この場合には-90度($\frac{π}{2}$ラジアン)回転させた$\frac{e^{-θ_n i}-e^{+θ_ni}}{2(0-1i)}$の結果が$\sin(0→π)$と一致する。そう、$\sin(θ)$は「回転の方向がある(逆関数を備える)」奇関数なのである。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
#単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(-c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
#共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly1=(p1-m1)/2
ly2=(p1-m1)/(2*(0-1j))
u0=num.linspace(m.pi,0,31,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(m.sin(u0[nm]))
u2=num.array(u1)
print("Imaginal of $\frac{exp(-θ_n(0+1i))-exp(+θ_n(0+1i)))}{2}$=",num.round(ly1.imag,8))
print("Real of $\frac{exp(-θ_n(0+1i))-exp(+θ_n(0+1i))}{2*(0-1i)}=",num.round(ly2.real,8))
print("$\sin(0→π)$=",num.round(u2,8))
Imaginal of $\frac{exp(-θ_n(0+1i))-exp(+θ_n(0+1i)))}{2}$
[-0. -0.10452846 -0.20791169 -0.30901699 -0.40673664 -0.5
-0.58778525 -0.66913061 -0.74314483 -0.80901699 -0.8660254 -0.91354546
-0.95105652 -0.9781476 -0.9945219 -1. -0.9945219 -0.9781476
-0.95105652 -0.91354546 -0.8660254 -0.80901699 -0.74314483 -0.66913061
-0.58778525 -0.5 -0.40673664 -0.30901699 -0.20791169 -0.10452846
-0. ]
Real of $\frac{exp(-θ_n(0+1i))-exp(+θ_n(0+1i))}{2*(0-1i)}$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
$\sin(0→π)$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
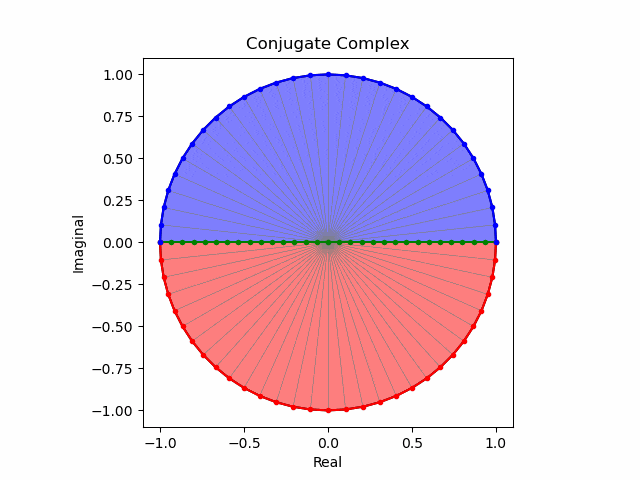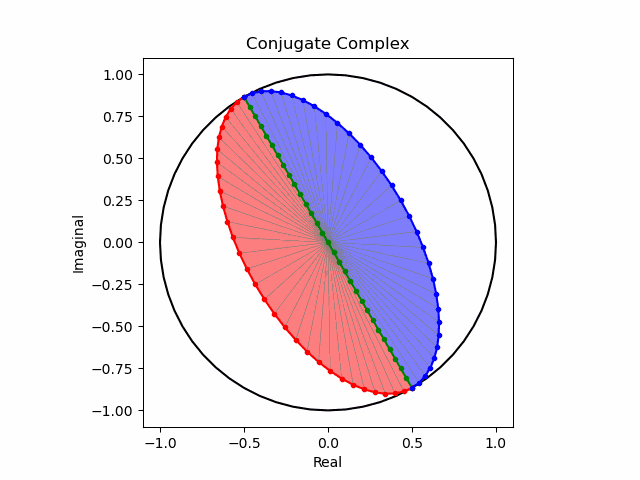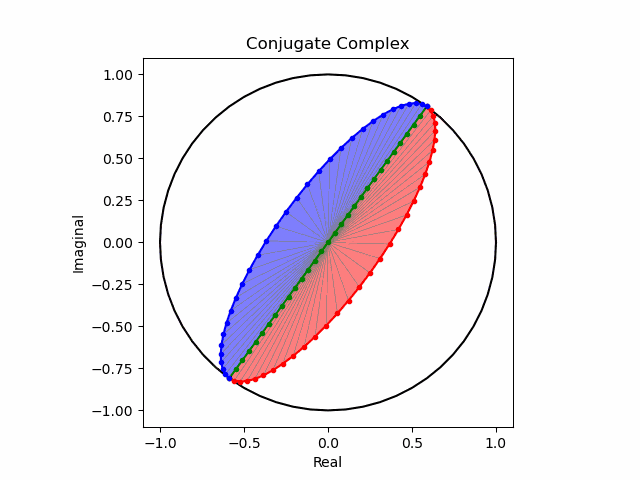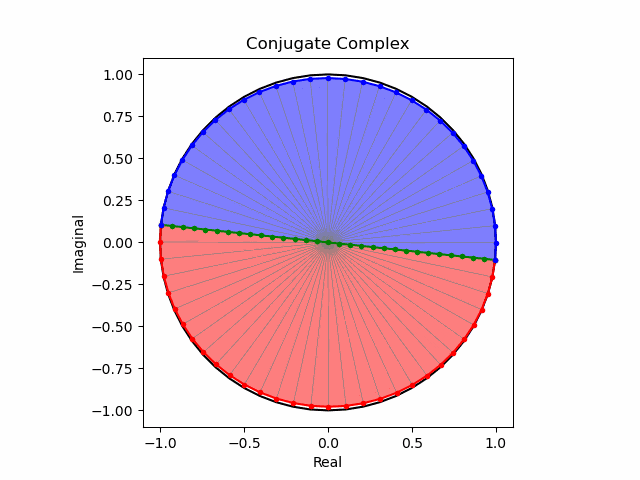
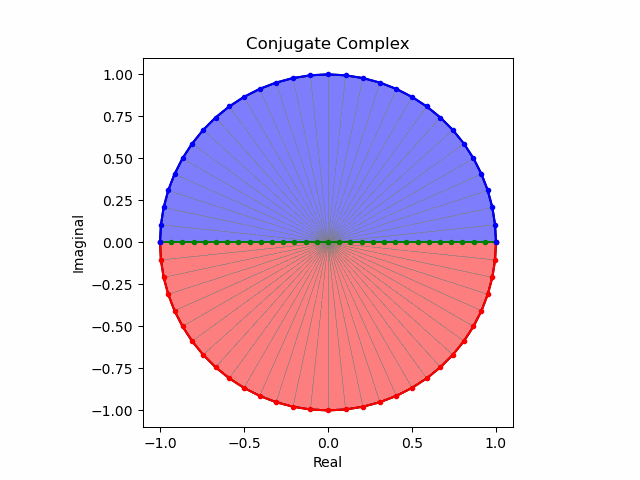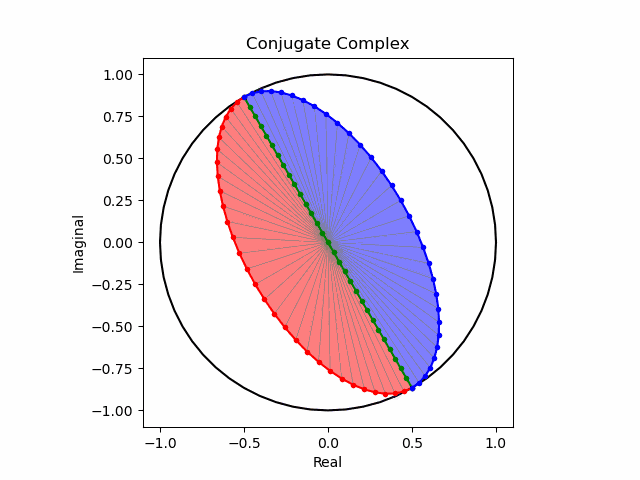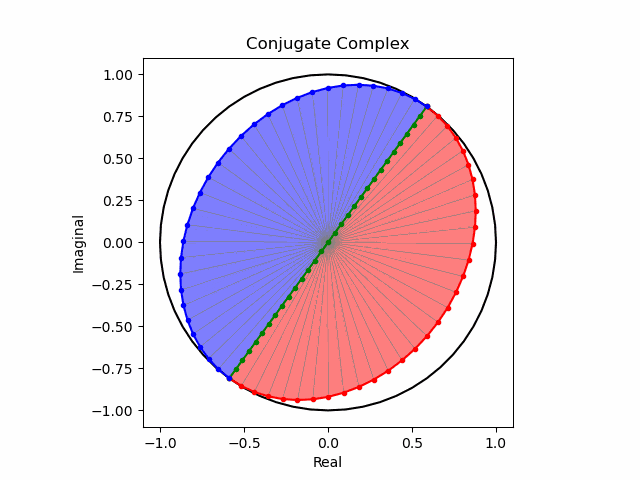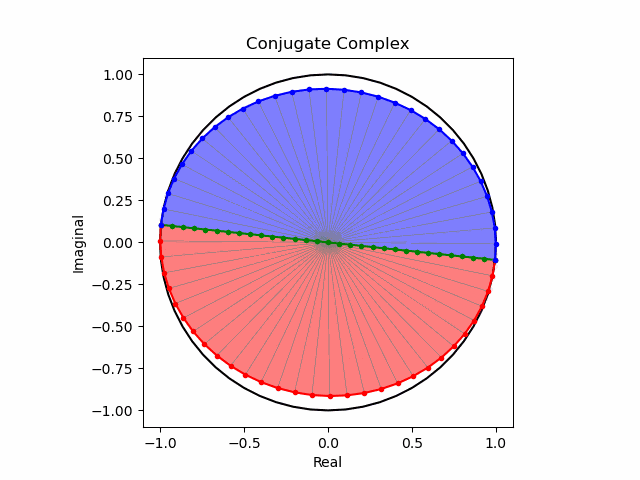
そしてこの様な「符号の向きが違うだけの一対」を複素共役(Complex Conjugate)という。
###任意の方向への回転と複素共益の全方向化
これでオイラーの公式(Eulerian Formula)$e^{θi}=\cos(θ)+\sin(θ)i$を用いて上掲の8位相を全方向に拡張する準備が整った。逆をいえば、この範囲でなら$\frac{1}{2}$や$\frac{5}{4}$といった小数点下を含む階数の微積分も可能という事になる。
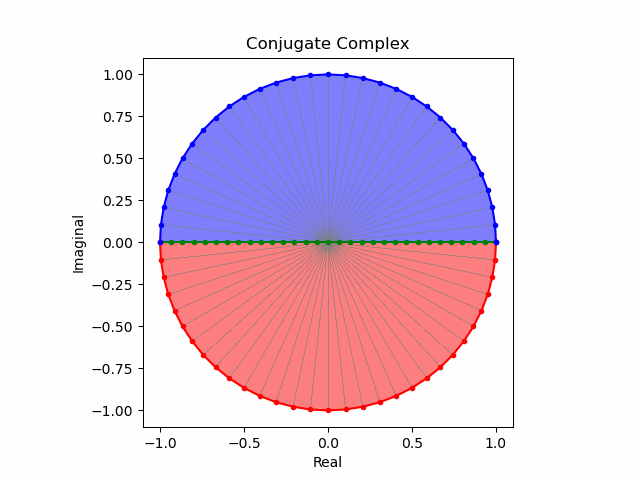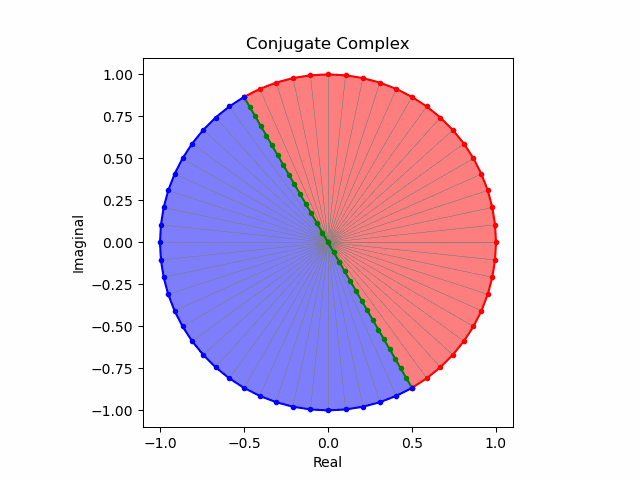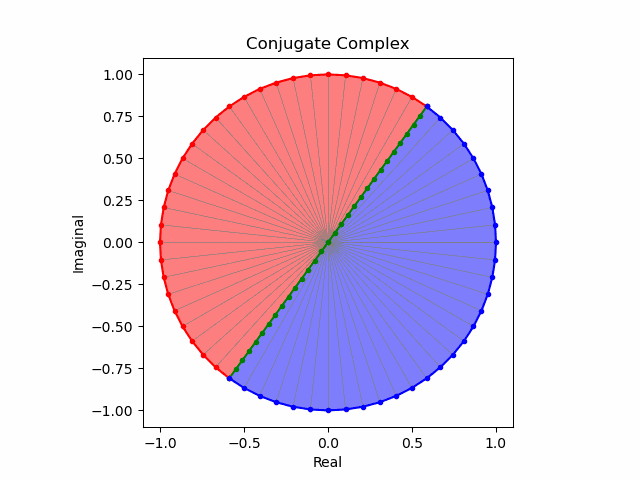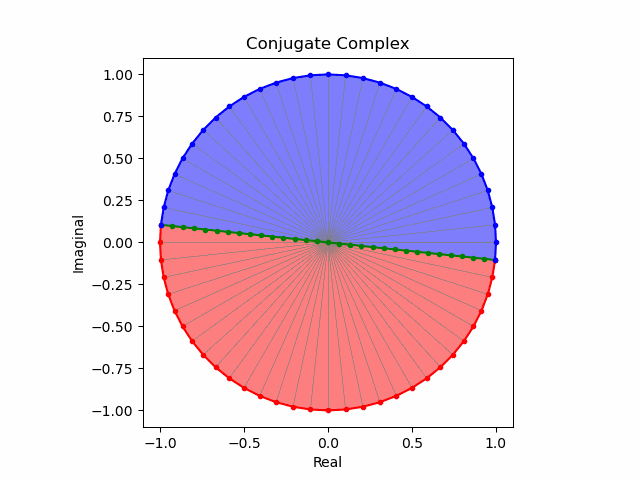
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
#複素円データ作成
c0=num.linspace(0,2*m.pi,61,endpoint = True)
c1=[]
for nm in range(len(c0)):
c1.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
c2=num.array(c1)
#単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(c.exp(zp[nm]*m.pi/2)*(0-1j))
p1=num.array(p0)
#共役複素数列(-)
m1=-p1[::-1]
#グラフ表示準備
plt.style.use('default')
fig = plt.figure()
#関数定義
def Conjugate_Complex(n):
plt.cla()
#座標変換
z2=[]
for nm in range(len(z)):
z2.append(z[nm]*c2[n])
z3=num.array(z2)
p2=[]
for nm in range(len(p1)):
p2.append(p1[nm]*c2[n])
p3=num.array(p2)
m2=[]
for nm in range(len(m1)):
m2.append(m1[nm]*c2[n])
m3=num.array(m2)
#スポーク描画
for nm in range(len(c2)):
plt.plot([0,c2[nm].real],[0,c2[nm].imag],color="gray",lw=0.5);
#円描画
plt.plot(z3.real,z3.imag,color="green", marker=".")
plt.plot(p3.real,p3.imag,color="red", marker=".")
plt.plot(m3.real,m3.imag,color="blue", marker=".")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Conjugate Complex")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
#塗りつぶし
p4=num.concatenate([p3,z3])
m4=num.concatenate([m3,z3])
plt.fill(p4.real,p4.imag,facecolor='red',alpha=0.5)
plt.fill(m4.real,m4.imag,facecolor='blue',alpha=0.5)
ani = animation.FuncAnimation(fig, Conjugate_Complex, interval=50,frames=60)
ani.save("output103.gif", writer="pillow")
①かかる全方向性は微積分の影響を受けない自然指数関数(Natural Exponential Function)$e^x$の0次元性(それ自体は観測対象とならない観測原点0と観測極限$\infty$を結ぶ観測線を半径とする円弧状/球面上の曲座標系)によって担保される。
【数理考古学】とある実数列(Real Sequance)の規定例③オイラーの等式(Eulerian identity)e^πi=-1が意味するもの？
- 自然対数関数$e^{x}$の微積分（どう回しても結果は同じ）
e^{x}\frac{d^n}{dθ^n}=(e^{x},e^{x},e^{x},…)\\
\int \int \int … \int e^{x}(dθ)=(e^{x},e^{x},e^{x},…)
②これに虚数(Imaginal)$i^2=-1$のiを掛けた範囲が乗法単位元(Multiplicative Identity)1を半径(Radius)とする単位円(Unit Circle)/単位球面(Unit Sphere)を構成する。
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」？
- 円描画関数$e^{θi}$の微積分（それぞれが±90度の変遷に対応）
e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log θi),-e^{ix},-i e^{i x}(\log θi),e^{ix},…)\\
\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log θi),- e^{i x},i e^{i x}(-\log θi),e^{ix},…)
これを可視化するには、水平面から観察すると直径(Diameter)の概念と完全に重なる単振動(SV=Simple vibration)$SV_n(n=1→-1)$が回転しているイメージから一旦離れ、水平面から観察すると半径(Radius)の概念と部分的に重なる$\sin(θ)$が回転しているイメージに移行すれば良い。この考え方の導入により回転角θ(物理学でいうところの角速度ω)の概念がとりあえず無視可能となる。
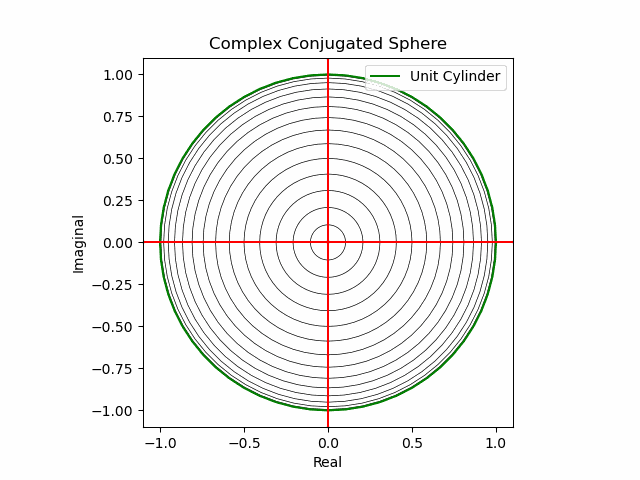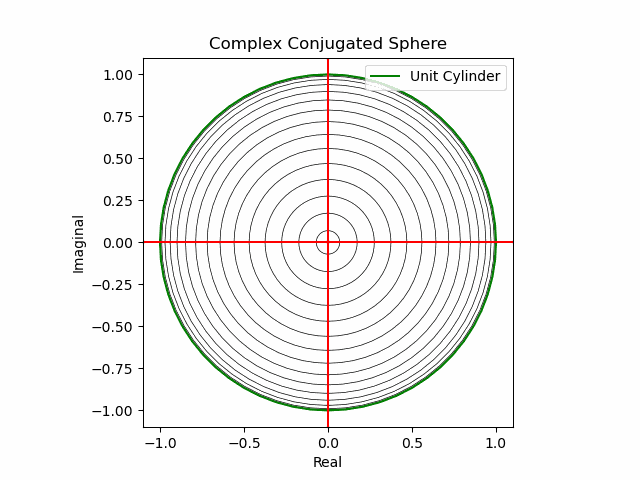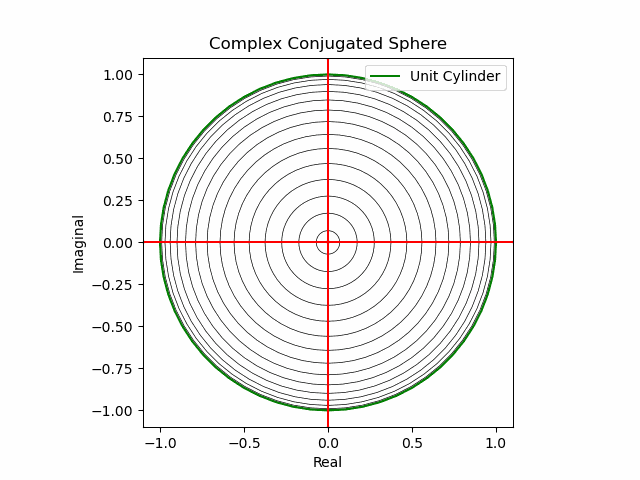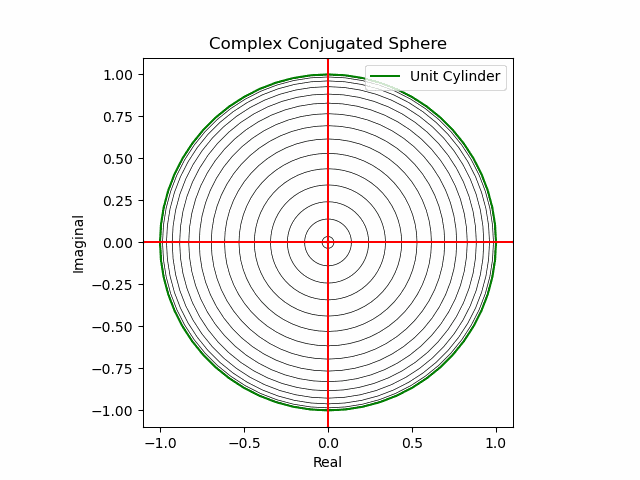
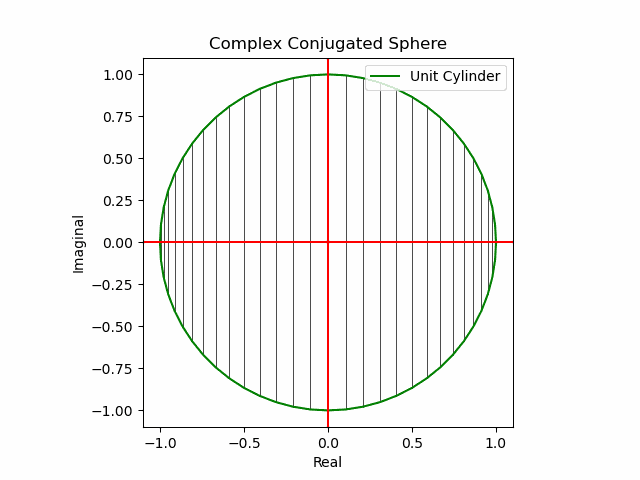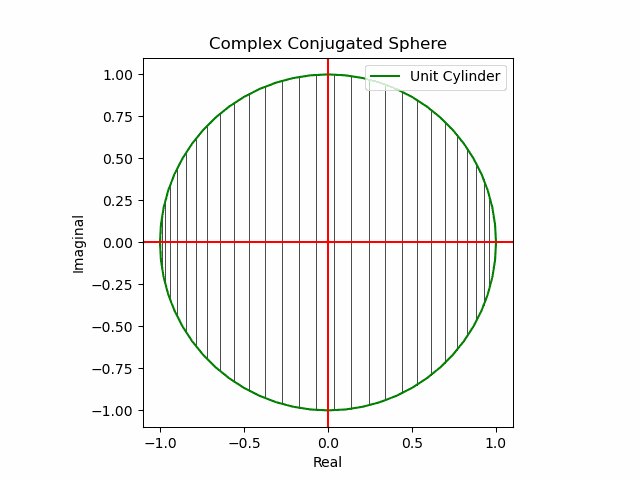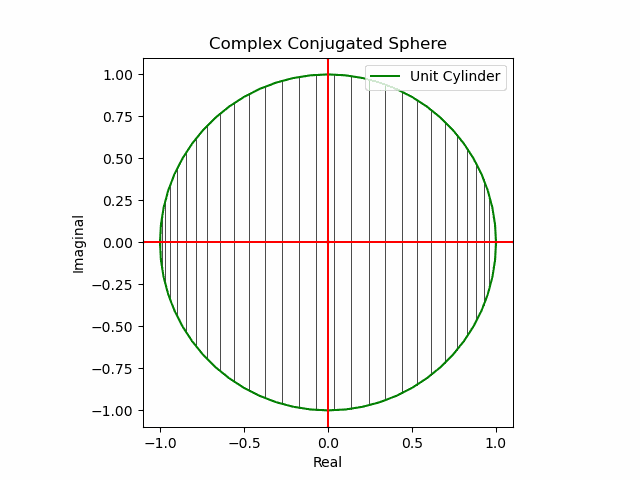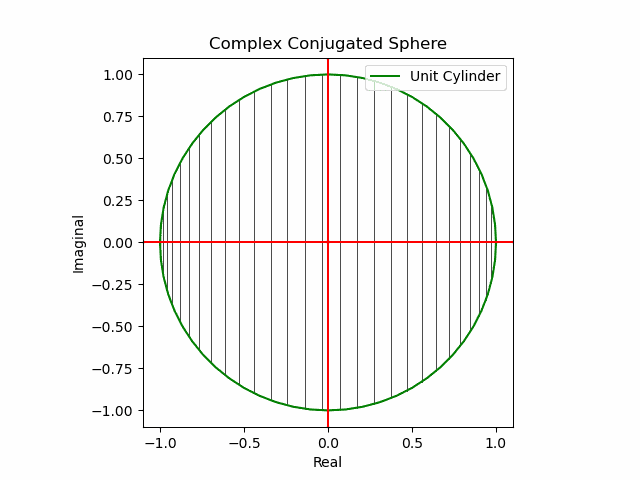
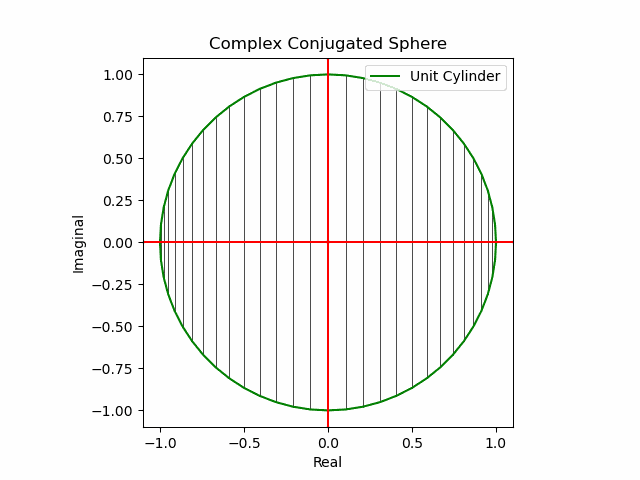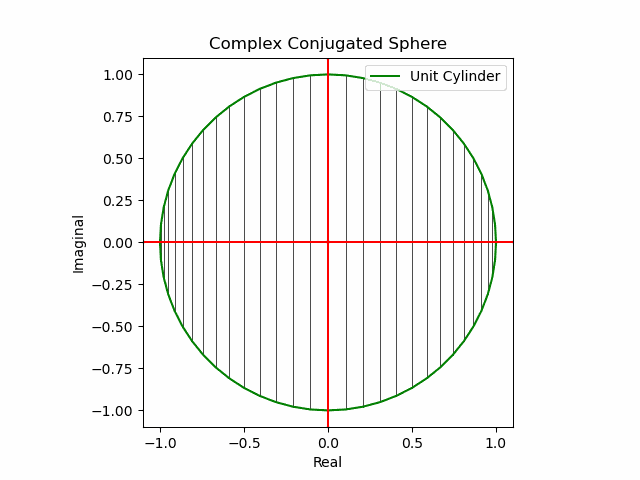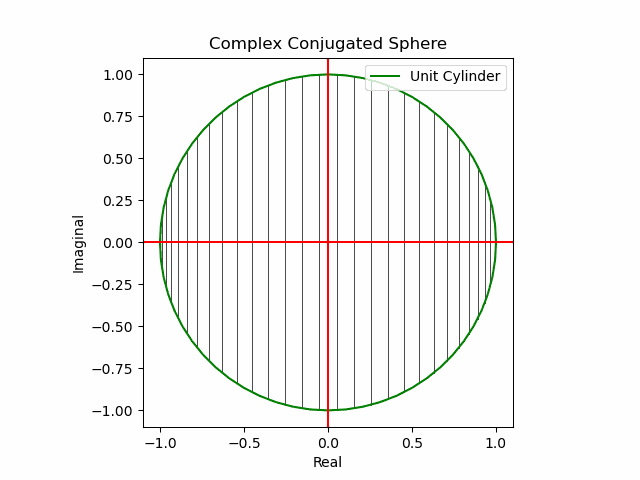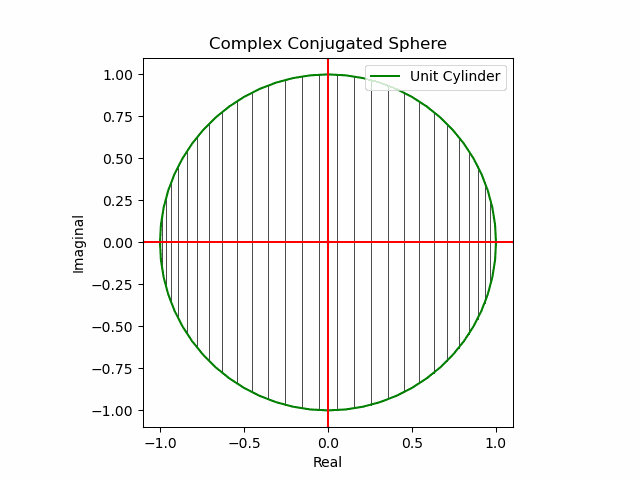
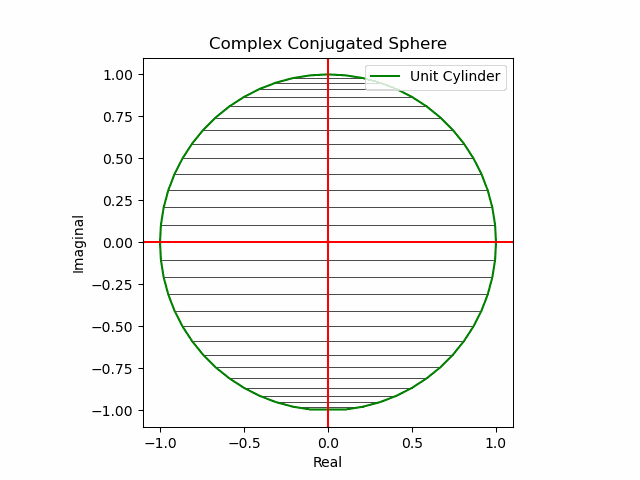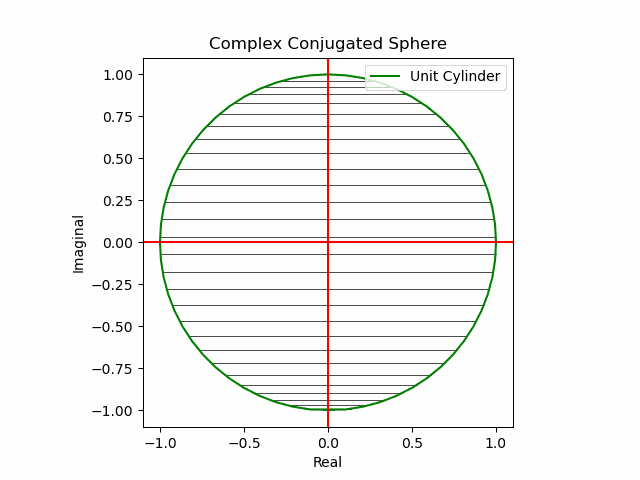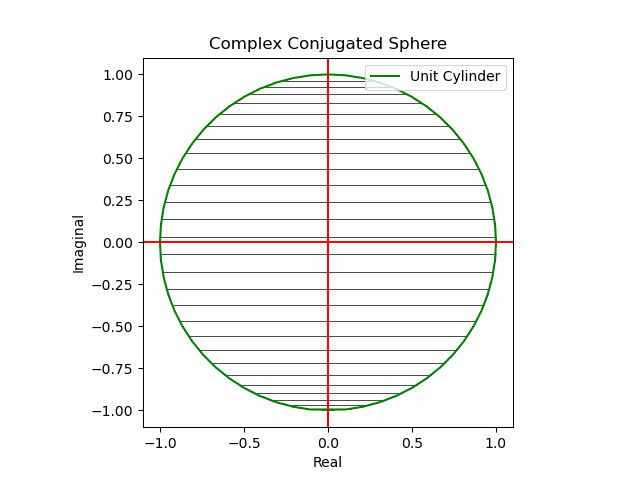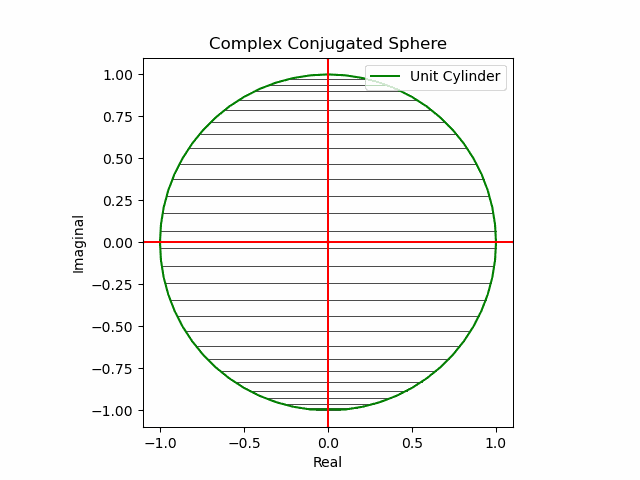
【初心者向け】複素共役（Complex Conjugate）のアニメーション表示について。
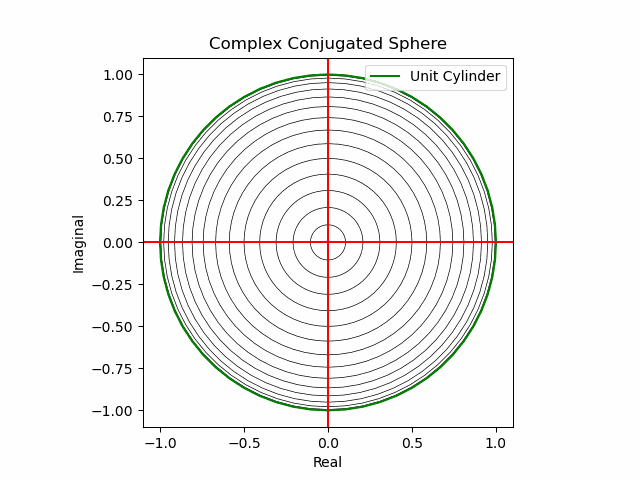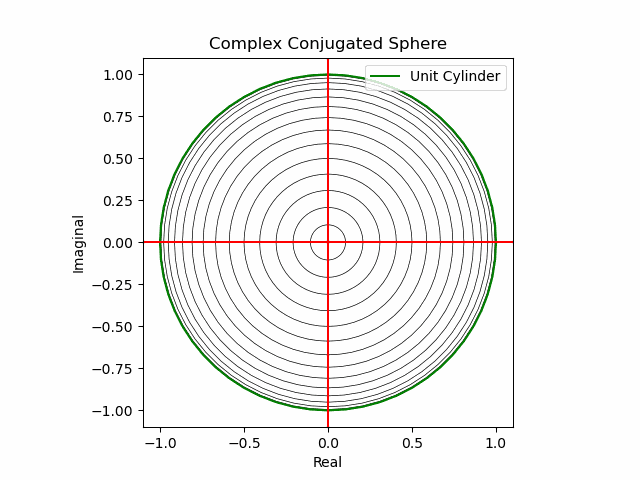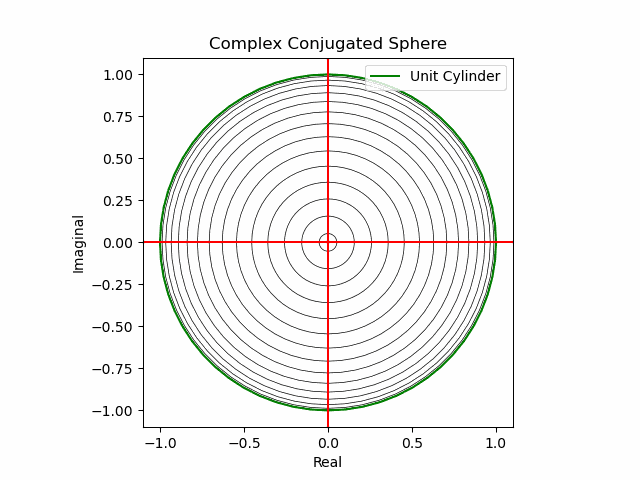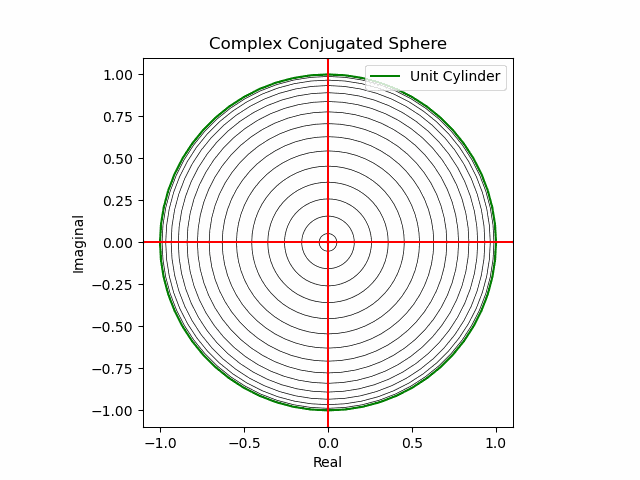
xy軸に沿った同心円展開
アニメーション化(内側→外側、中割り二枚)
アニメーション化(外側→内側、中割り二枚)
アニメーション化(どちらにも見える、中割り一枚)
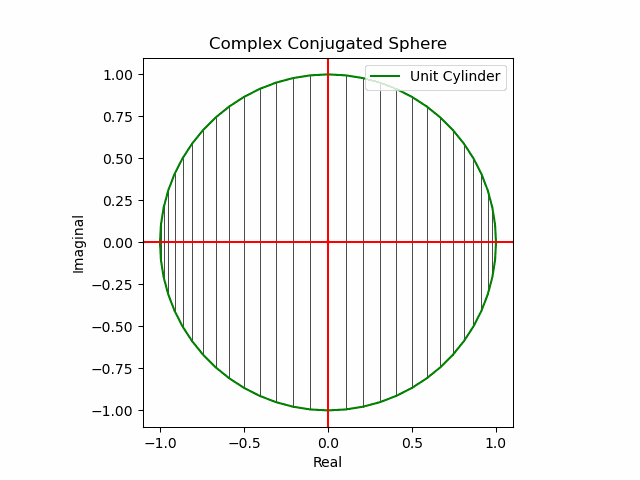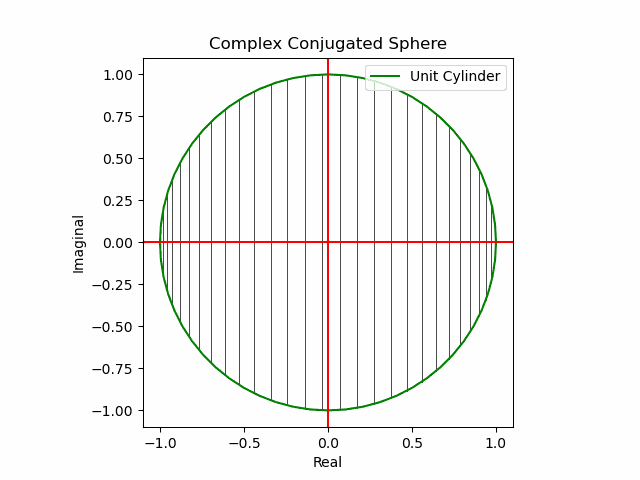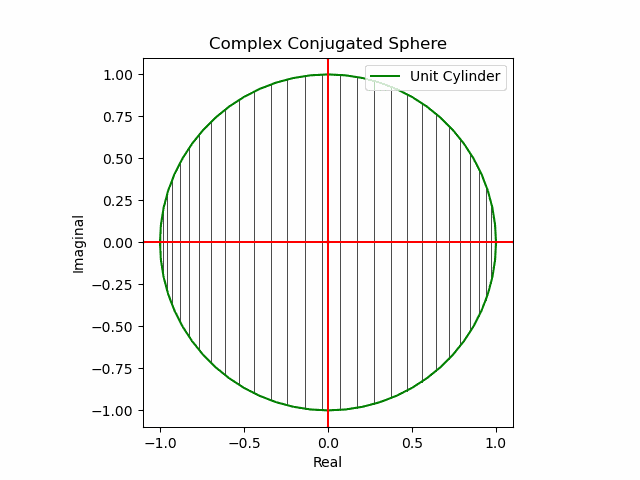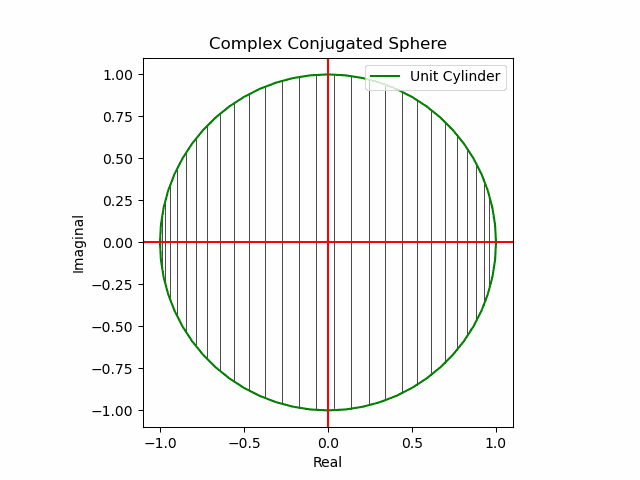
x軸に沿った側面展開
アニメーション化(y=+1→-1、中割り二枚)
アニメーション化(x=y=-1→+1、中割り二枚)
アニメーション化(どちらにも見える、中割り一枚)
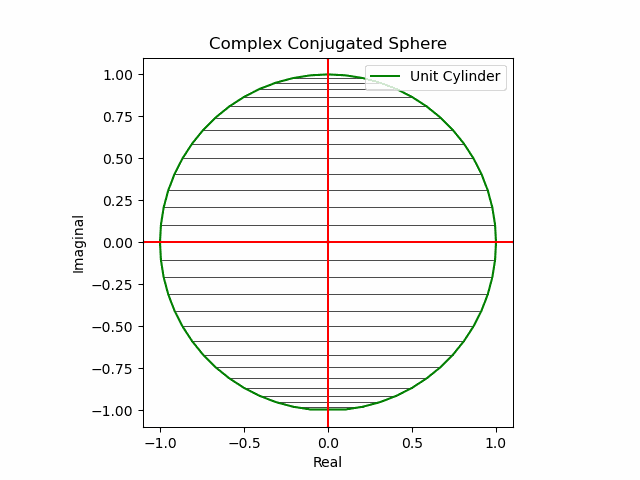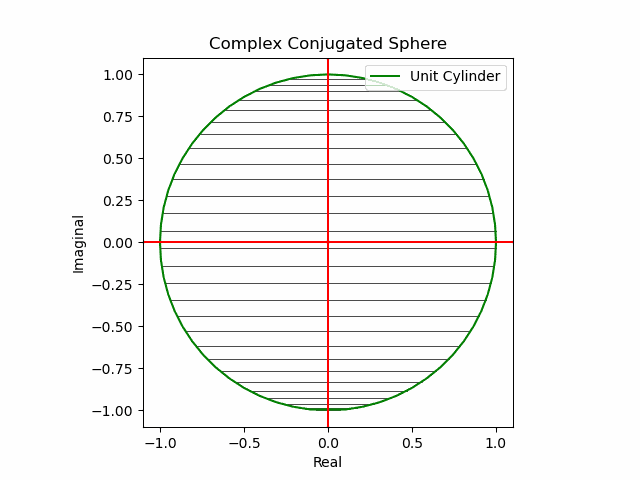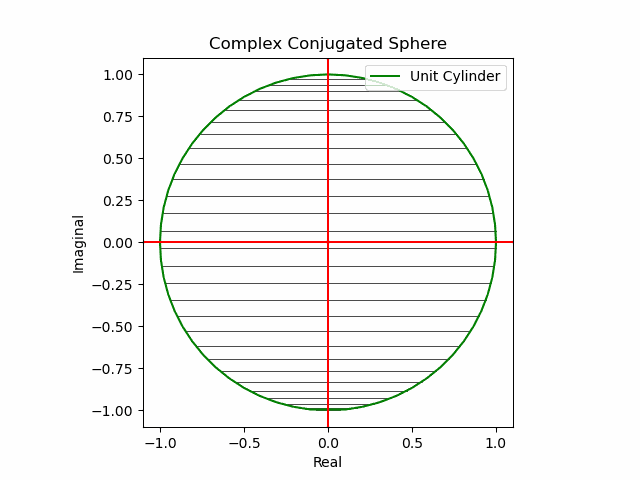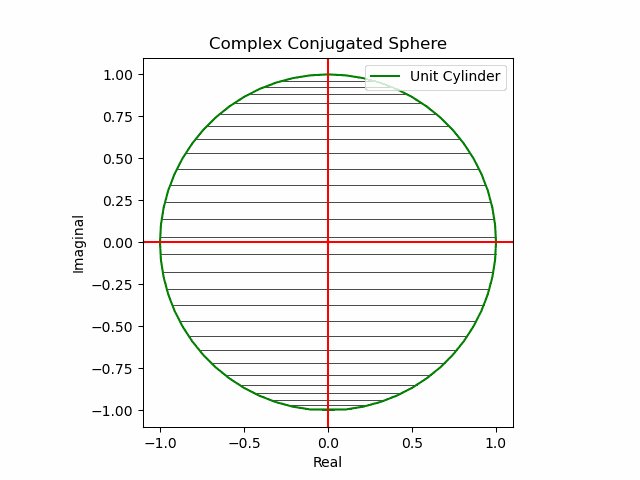
y軸に沿った側面展開
アニメーション化(y=+1→-1、中割り二枚)
アニメーション化(x=y=-1→+1、中割り二枚)
アニメーション化(どちらにも見える、中割り一枚)
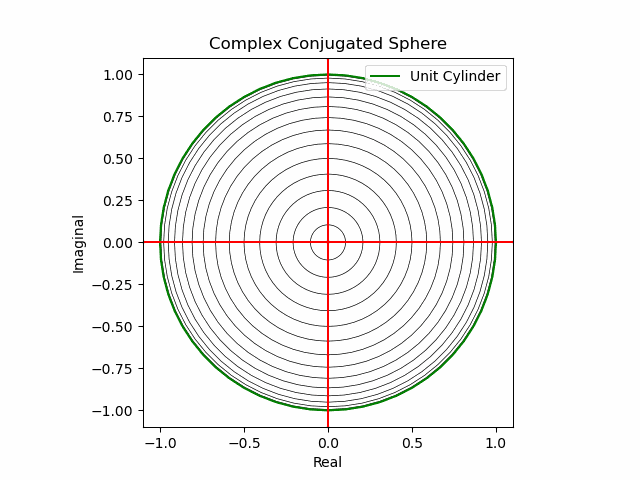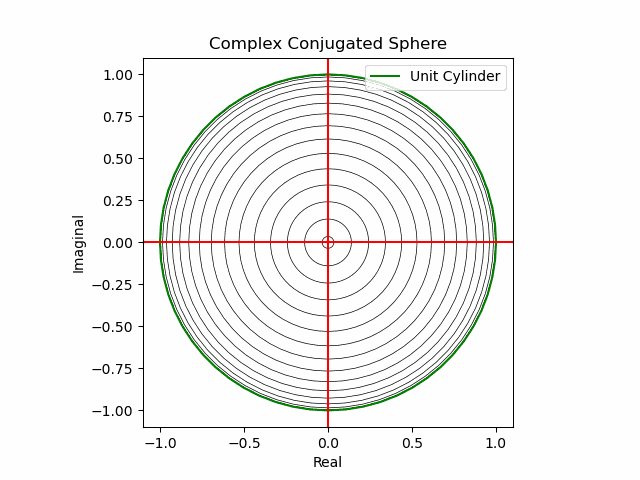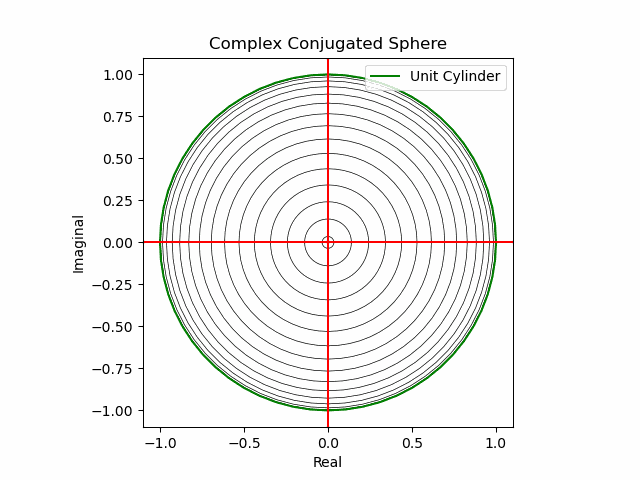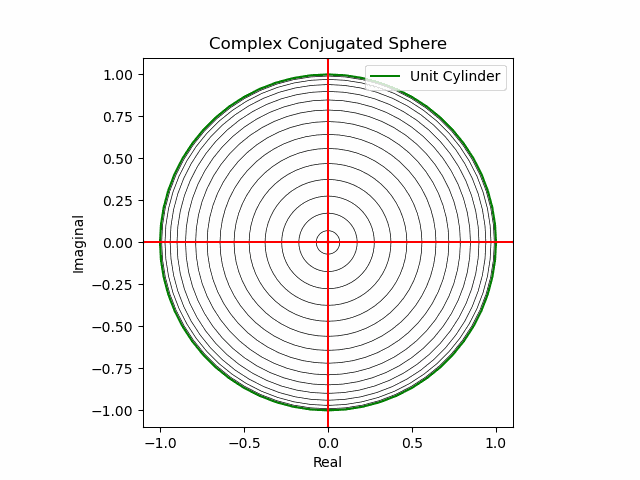
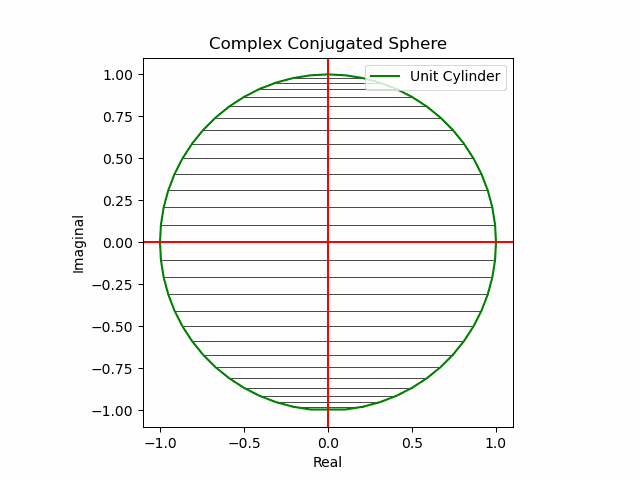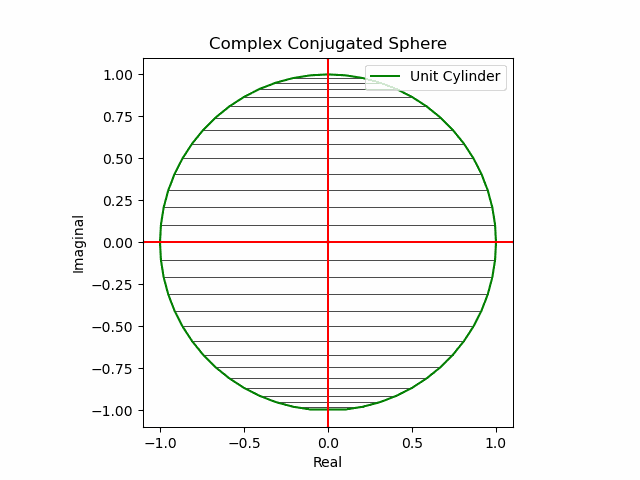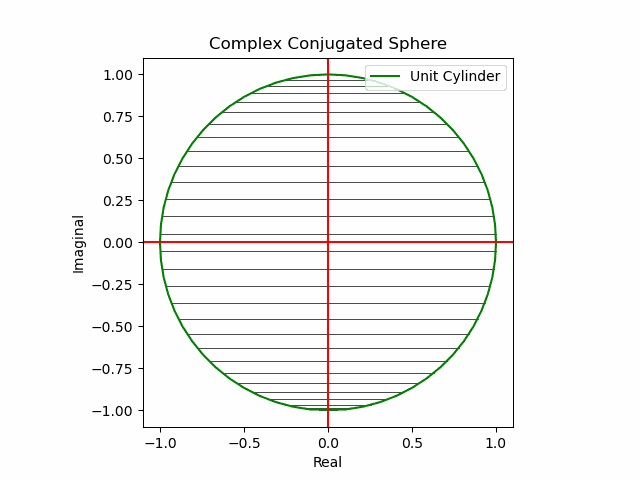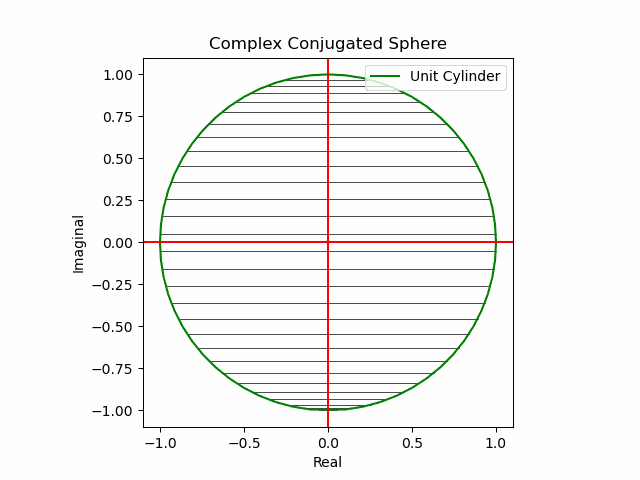
その結果、後に残るのはXYZ軸の様な任意の三次元直交軸それぞれを回転軸として(ただし回転方向は不確か)放射線状に全方向に向けて展開する共役線(Conjugated Line)のみとなる。とりあえずこれを以降「複素共役球面(Complex Conjugated Sphere)」と呼ぶ事にしよう。
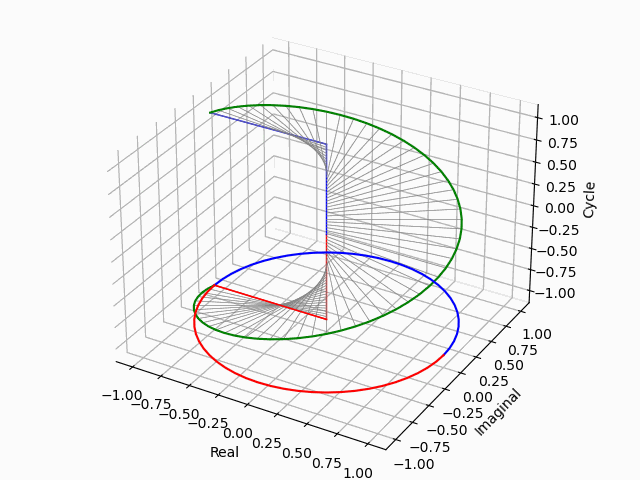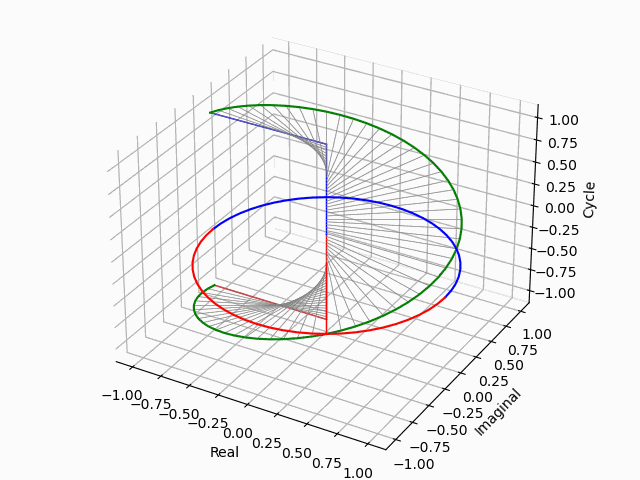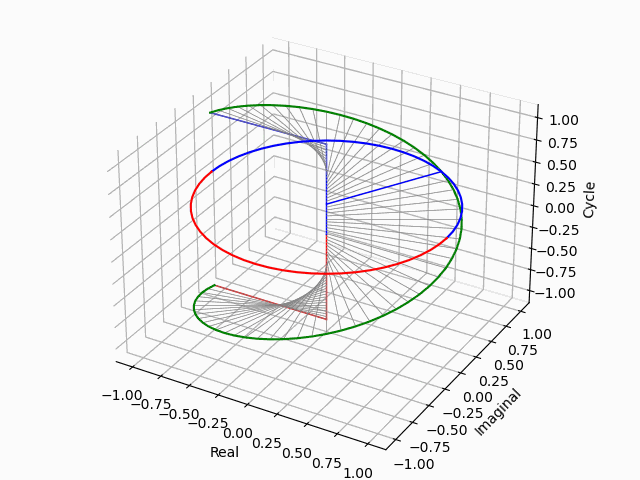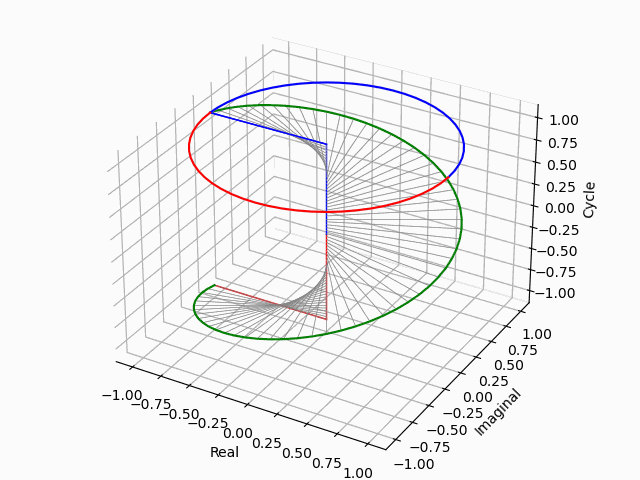
###さらにz軸のパースペクティブを追加
この考え方を援用すればさらに「z軸のパースペクティブ」を追加する事も出来る。
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。
まずは円の縦軸を単純振動の周期で伸縮させてみた場合。
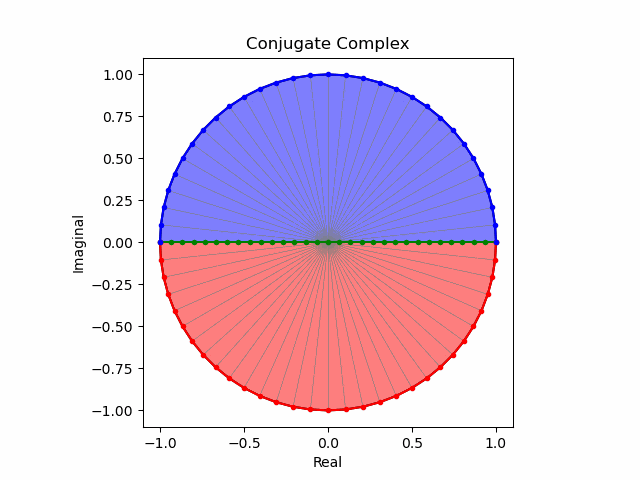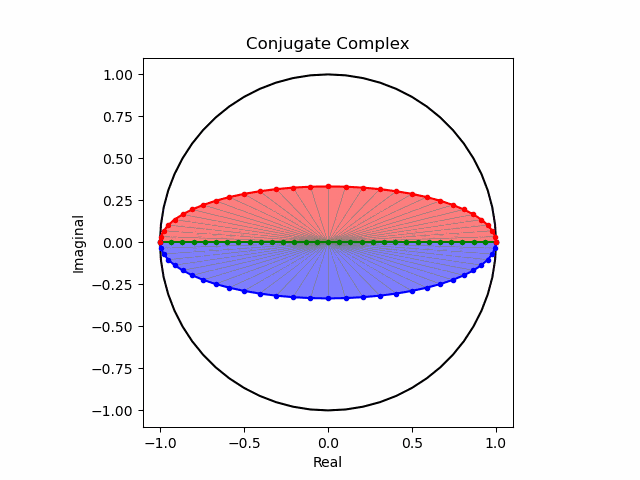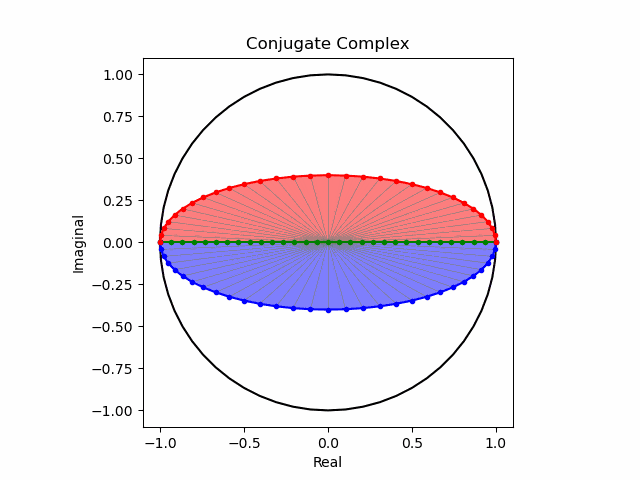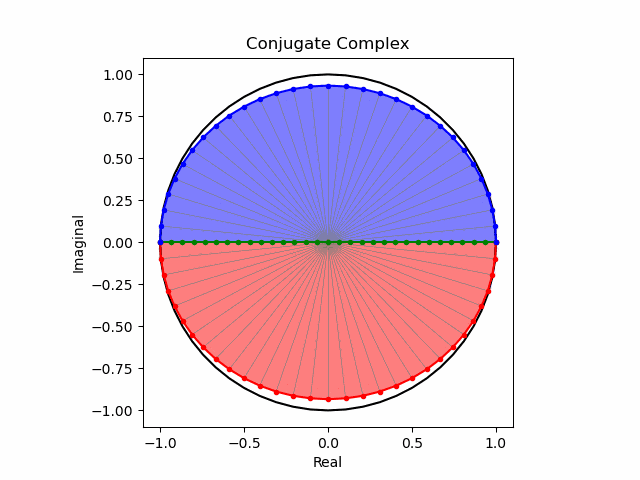
次いで$\cos(θ)$の周期で伸縮させてみた場合。
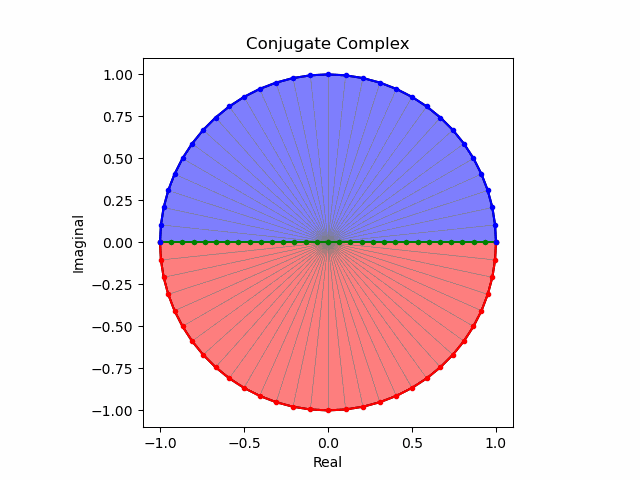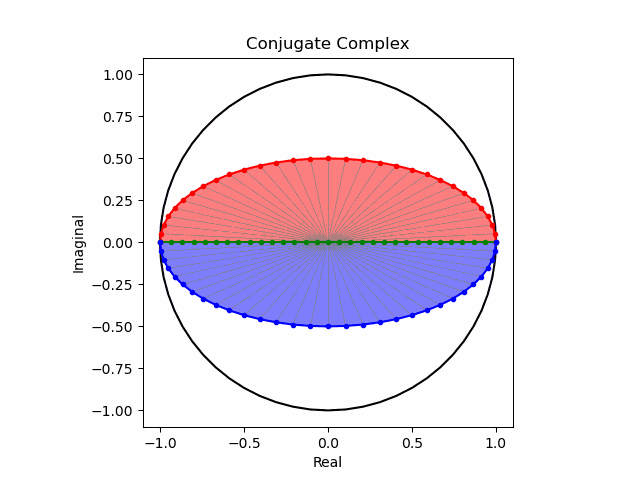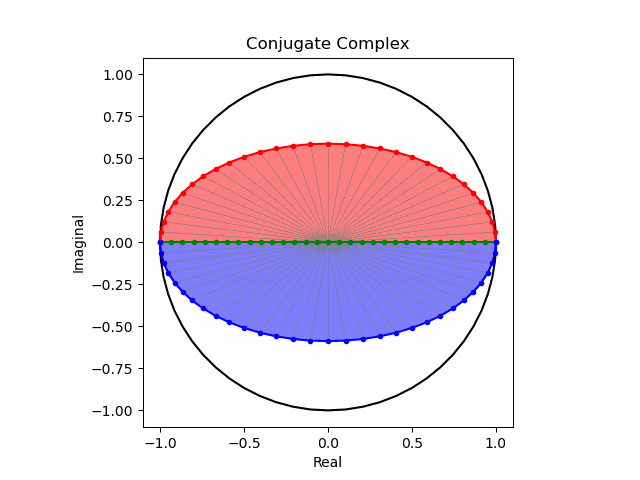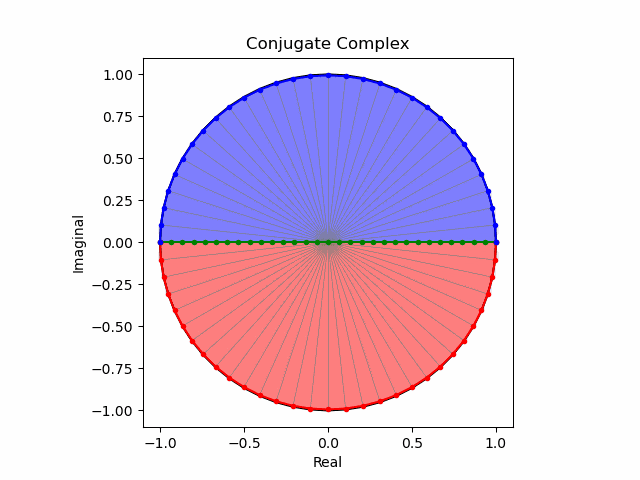
円盤の回転がそれほど滑らかになった様に見えないのは、人間の視覚による補正能力の高さを意味しているのかもしれない。ちなみにこの垂直回転と上掲の水平回転と組み合わせたものが四元数(quaternion)$w+i+j+k$におけるortho-split/sympletic form表現となり、xyz軸から完全に離れた回転表現が可能となる。確かに言われてみれば緯度経度などにも採用されている三次元曲座標系において垂直角θは水平角φの半分しか使わないが、この座標系では全周分使い切るのである。
Rで四元数
PythonでQuaternionを使う ~ numpy-quaternion ~
角度θと角度φの角速度wの比率が1:2の時
角度θと角度φの角速度wの比率が1:4の時
#等速円運動(物理学)と複素平面(数学)の概念の統合
以下の様に考えれば、等速円運動と複素平面の概念が統合されます。
以下の記事がヒントになって辿り着いたパラダイムシフトで、私にとっては、まさしく「コロンブスの卵」となったのです。
【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！
①$e^{iθ}$を微分すると$e^{iθ}$にiを掛けたものとなる。図で示すと、青いベクトルの先の点での速度が赤い遠心力ベクトルとなる。
f(θ)=e^{iθ}\\
f′(θ)=ie^{iθ}
②さらに$ie^{iθ}$を微分すると$-e^{iθ}$になる。図で示すと、赤い速度ベクトルに対する緑の向心加速度(Centripetal Acceleration)ベクトルが検出される。要するにこれが物理学における等速円運動の数学的表現なのである。
f(θ)=ie^{iθ}\\
f′(θ)=-e^{iθ}
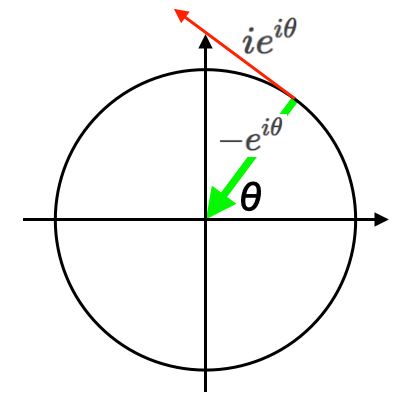
何とあっけない…気づいてさえしまえば、単なる自明の場合(Trival Case)に過ぎません。
そんな感じで以下続報…