【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
【数理考古学】とある実数列の規定例③オイラーの等式e^πi=-1が意味するもの?
ここでまとめた「実数と虚数の関係」は、実はフーリエ級数/フーリエ変換(逆変換)/ラプラス変換(逆変換)の歴史そのものだったりする訳です。
フーリエ級数(Fourier Series)の世界
熱伝導方程式の一部としてそれが発表されたのは1807年~1822年とされている。
フーリエ級数研究の系譜をたどって
群の条件を満たす(すなわち単位元と逆元が存在し、結合法則が成立し、演算結果が閉じている)無限関数列であるが、その制約ゆえに周期性のある整数倍の周波数しか扱えない。
【初心者向け】群論概念①基本定義

①この概念の研究史自体は17世紀、すなわちニュートン・メルカトル級数(Newton-Mercator Series,1668年)や(テイラー級数/マクローリン級数発見の原点となった)ライプニッツ級数(Leibniz Series,1674年)/グレゴリー級数(Gregory Series,1671年)における交代級数(Alternating Series)$-1^x$の概念発見にまで遡る。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数
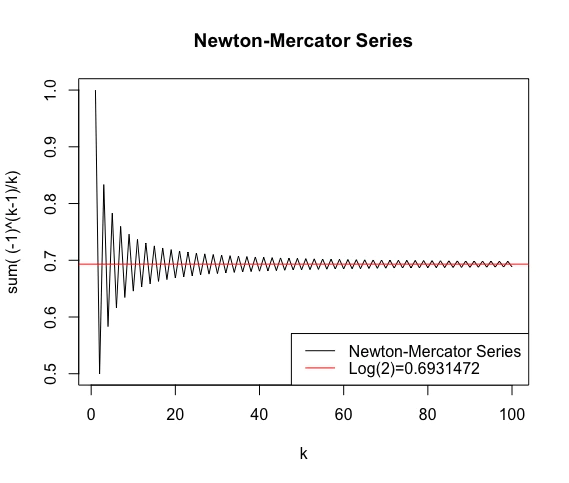
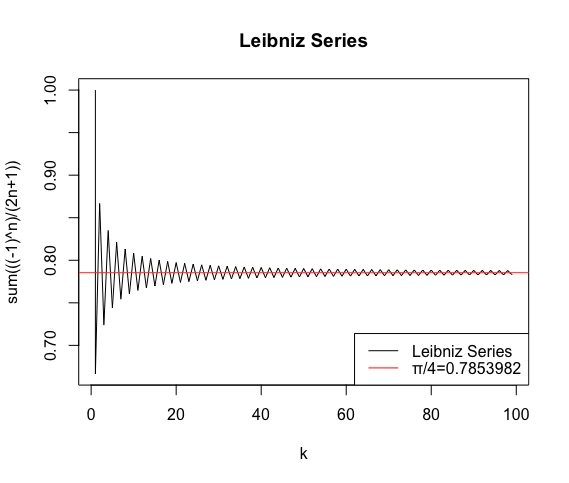

この様にグレゴリー級数の収束は極めて遅いので、それに業を煮やしてオイラー変換(Eulerian Transformation)が開発された。これによって$log(2)$の値も求めやすくなった。ねぇ、本当にオイラーはブルバキみたいな集団ペンネームじゃないの?
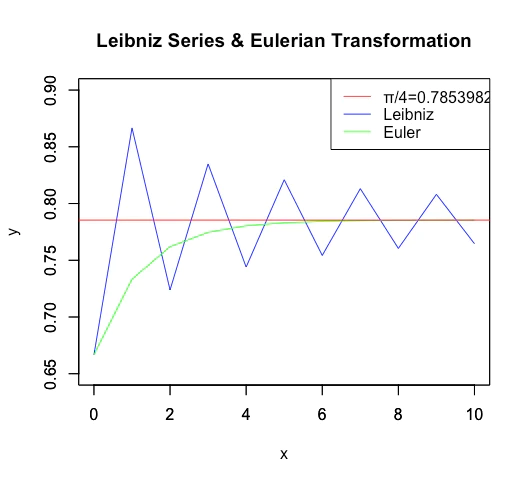
こうした級数の研究がテイラー級数 (Taylor Series,1715年)やマクローリン級数(Maclaurin Series,18世紀)の発明とオイラーの公式(Eulerian Formula)$e^{θi}=\cos(θ)+\sin(θ)i$発見に結びつくのである。
②フーリエ級数は(等差数列/等比数列/テーラー級数/マクローリン級数の流儀に従って)計算の及ばなかった一般項を残余項=誤差範囲として示す。
【初心者向け】フーリエ解析(Fourier Analysis)を可視化する。








③この様に、複素数概念導入は級数段階から始まるのである。
フーリエ変換 - Wikipedia
フーリエ変換を考える動機はフーリエ級数の研究に始まる。フーリエ級数の研究において、複雑な周期関数は単純な波動の数学的な表現である正弦関数$\sin(x)$や余弦関数$\cos(x)$の和として表される。正弦や余弦の性質のおかげで、この和に現れる各波の量、フーリエ係数を積分によって計算することができる。多くの場合に${\textstyle e^{2\pi i\theta }=\cos {2\pi \theta }+i\sin {2\pi \theta }}{\textstyle e^{2\pi i\theta }=\cos {2\pi \theta }+i\sin {2\pi \theta }}$(オイラーの公式)を用いて、正弦関数および余弦関数の代りに基本波動${\textstyle e^{2\pi i\theta }}{\textstyle e^{2\pi i\theta }} $を用いた方が便利である。この場合には多くの公式が簡単化され、本項で後述するフーリエ変換のほかの類似の定式化をあたえるという点に優位性がある。この正弦・余弦から複素指数関数への移行にはフーリエ係数が複素数値であることを要する。この複素数は、関数に含まれる波動の振幅(あるいは大きさ)と、位相(あるいは初期角)の両方を与えているものと通常は解釈される。また、この移行に際して「負の周波数」の概念も導入される。例えば、波動 ${\textstyle e^{2\pi i\theta }}{\textstyle e^{2\pi i\theta }} $および${\textstyle e^{-2\pi i\theta }}{\textstyle e^{-2\pi i\theta }} $はともに周期1を持つが、複素フーリエ級数においては別々の成分として取り扱われる。したがって、周波数を単純に周期の逆数と考えることはできなくなる。
- なるほど、上掲の投稿における「正負の概念導入に伴う視座の2分割」は、この次元ではこう説明される訳である。
- 離散的とはいってもここでいう「整数倍の目盛り」はどこまでも細かく刻んでいける。そうした意味合いも含め、まさに上掲の投稿における「整数族」概念の大源流。
フーリエ変換/逆変換(Fourier Transform(FT)/Inverse Transform)の世界
上掲のフーリエ級数より「離散的で有限である」制約を取り除き、無限範囲を連続的に扱える様にした座標系「周波数領域」を想定し、「時間領域(現実同様に時間が流れる物理的空間)」との間をフーリエ変換とフーリエ逆変換によって往復する。その全体像はまさにWikipediaにあるアニメーションのイメージ通り。
フーリエ変換/逆変換の公式は以下です。
フーリエ変換
F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t}dt\\
f(t)=\frac{1}{2π} \int_{-\infty}^{\infty} F(\omega) e^{-i \omega t}d\omega
これを以下の様に表します。
F(\omega)=\mathcal{F}[f(t)]\\
f(t)=\mathcal{F}^{-1}[F(\omega)]
フーリエ変換の最大の特徴はその線形性や推移性に加え(そもそもフーリエ級数が無限連続微積分の演算結果集合である事から)微分や積分が四則演算で扱える範囲に入ってくる事です。
フーリエ変換の性質
線形性
\mathcal{F}[af(t)+bg(t)](\omega)=a\mathcal{F}[f(t)](\omega)+b\mathcal{F}[g(t)](\omega)
対称性
\mathcal{F}[2πf(-\omega)](\omega)=F(t)\\
\mathcal{F}^{-1}[F(t)](\omega)=2πf(-\omega)
相似定理(時間軸の伸縮)
\mathcal{F}[f(at)]→\frac{1}{|a|} F(\frac{\omega}{a})\\
\mathcal{F}^-1[(\frac{1}{|a|} F(\frac{\omega}{a})] → f(at)
推移性
\mathcal{F}[f(t+t_0)](\omega)=e^{it_0\omega}\mathcal{F}(\omega)\\
\mathcal{F}[f(t)e^{i\omega_0\omega}](\omega)=\mathcal{F}(\omega-\omega_0)
微分則
\mathcal{F}[\int_{t}^{\infty}\frac{d}{dt}f(t)dt](\omega)=i\omega\mathcal{F}[f(t)](\omega)
積分則
\mathcal{F}[f(t)](\omega)=\frac{1}{i\omega}\mathcal{F}[f(t)](\omega)
また有限周期の「揺らぎ」が捕まえられる一方、無限周期の$\cos(t)$波や$\sin(t)$波の振幅が無限に到達して捉えられないという特徴を有します。ある意味、この関係はヘヴィサイドのステップ関数と(その微分結果たる)ディラックのデルタ関数に対応するとも。
【数理考古学】ディラックのデルタ関数とヘヴィサイドのステップ関数
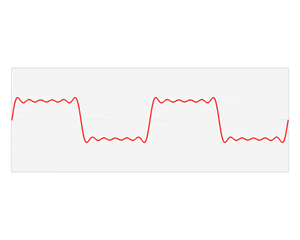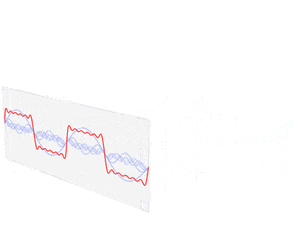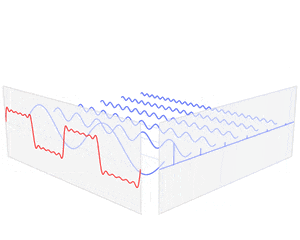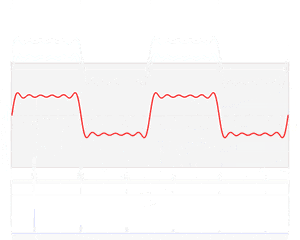
元波形(0.5秒分の20Hzの単振動波)

フーリエ変換後の波形
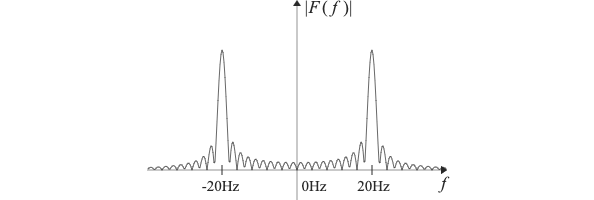
無限周期の20Hzの単振動波のフーリエ変換後の波形
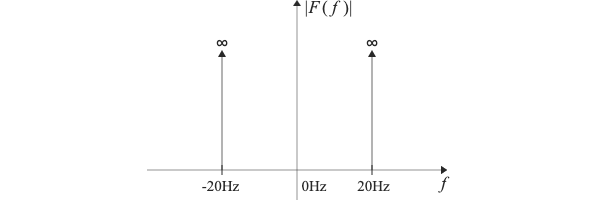
この影響でフーリエ変換の積(×)は「畳込み積(*)」と呼ばれる特殊な形となり、そこでデルタ関数($\delta(t)$)との関係も実際に生じてくるのです。
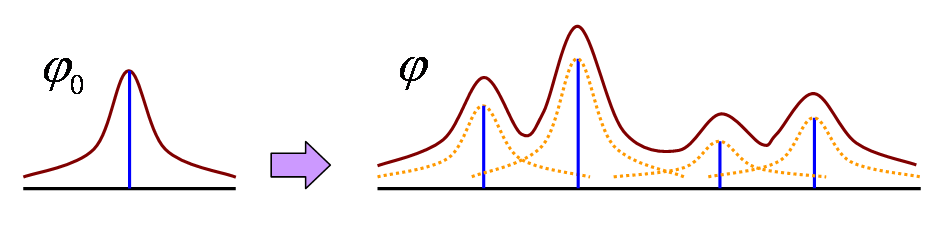
f*g(t) =\int_{-\infty}^{\infty}f(τ) g(t-τ)dτ\\
\mathcal{F}[f(t)×gt](\omega)=\mathcal{F}[f(t)](\omega)*\mathcal{F}[g(t)](\omega)\\
\mathcal{F}[f(t)*gt](\omega)=\mathcal{F}[f(t)](\omega)×\mathcal{F}[g(t)](\omega)\\
\delta(t \pm T)* f(t)=f(t \pm T)
マイナスの周波数が存在する理由は、周波数領域への変換過程で半分の周波数成分が数学的にマイナス側に移動するせいで、この時対称性の分岐点となる0Hzを直流成分という。
- ここでいう直流成分が上掲の投稿における「(実数列を想定する為の)中心の検出」概念に対応する。あくまで想定上の中心なので揺らぐ可能性があり、これが「特定の演算は演算結果集合と観測結果集合と一致している場合のみ成立する」条件に重なる。
離散フーリエ変換(Discrete Fourier Transform(DFT))の世界
実際にサンプリングによって得られる観測結果集合は離散的で有限の範囲に留まるので、そのリアルタイム処理に特化したフーリエ級数概念の独自拡張。時間領域に対応する「時間推移に伴う周波数領域(スペクトル)の変遷」を表示する。
イコライザGIF
コンピューター処理と相性が良く、現在単にフーリエ変換というと概ねそれ、すなわち高速フーリエ変換(FFT=Fast Fourier Transform)を指す。
離散フーリエ変換(DFT)の仕組みを完全に理解する
【数理考古学】音楽と離散フーリエ変換(DFT)
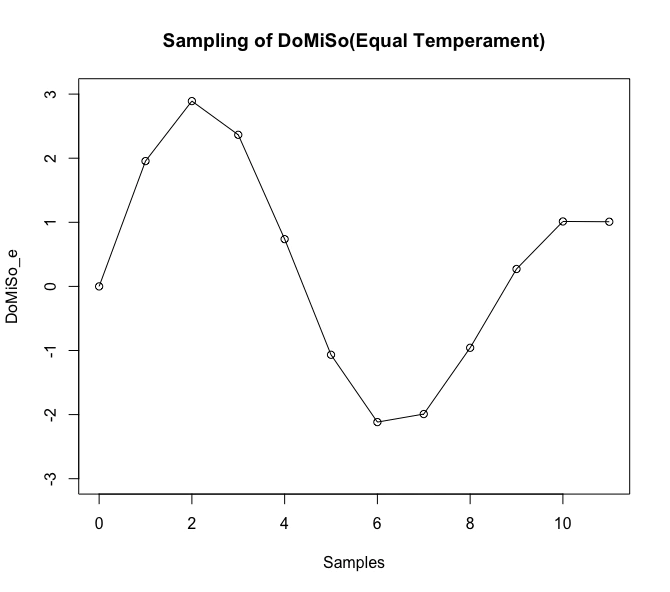
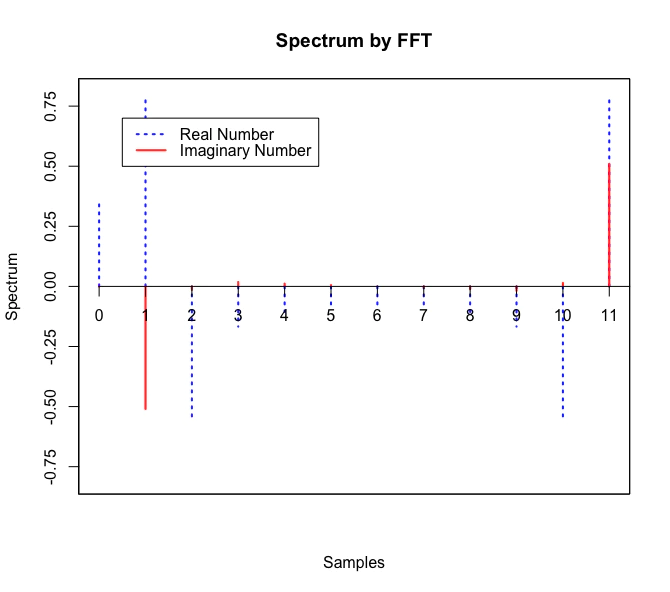
ラプラス変換/逆変換(Laplace Transform/Inverse Transform)の世界
ラプラス変換の定義は,時間tの関数をf(t)とすると以下となります。
F(s)=\int_{0}^{\infty} f(t) e^{-st} dt
この式は時間t の関数f(t) にを掛け合わせたものについてt=0から∞まで積分することでtの関数をsの関数F(s)に変換します。式中のsはラプラス演算子といいs>0で複素数も取り得ます(一方tは実数のみ)。ラプラス変換を数式記号を用いて示す場合は次のように記します。
F(s)=\mathcal{L}[f(t)]
ラプラス変換された関数F(s)を時間関数f(t)に再び変換することをラプラス逆変換といい、数式記号を用いて示す場合は次のように記します。
f(t)=\mathcal{L}^{-1}[F(s)]
ラプラス変換のイメージを絵的に説明すると,ラプラス変換によって得られるF(s)はf(t)と$e^{-st}$を掛け合わせたものについてt軸に挟まれたt=0から∞までの面積と考えることができます。図のグラフは時間関数 f(t)と$e^{-st}$を掛け合わせたもの(ラプラス積分の中身)について,時間的変化を示していますが、灰色に塗りつぶしている領域の面積がまさにF(s)と等価となります。
f(t)がt→∞で収束していますが、ラプラス変換が成立するにはプラス積分値(F(s))が収束する事が絶対条件で、それを実現する為に$e^{-st}$を掛けているのです。このように収束に起因する因子(ラプラス変換における)を収束因子といいます。ラプラス変換できない例としては,f(t)=exp(t^t)の場合は(exp(x)はexと同じ)ラプラス積分が∞に発散してしまうので,ラプラス変換出来ません。
フーリエ変換/逆変換のiω(ωは実数)の部分にs(sは複素数)を代入したのがラプラス変換です(要するに範囲無限を実現する為の方便の違い)。
ラプラス変換
フーリエ変換では、微分演算子はiωに、積分は1/iωに変換される。すなわち、ラプラス変換の変数sは微分演算子に相当する事になる。
- ラプラス変換は指数関数の部分に虚数が付いていない.
- ラプラス変換の式の積分範囲はt>0に限られている.
- ラプラス変換ではsの値は複素数の範囲で考えても良い.(しかしtは実数である)
- ラプラス変換では無理して物理的なイメージを考えない方がいい.
- ラプラス変換の逆変換の式はあるにはあるが,虚数軸に沿った無限積分が必要になる.
ラプラスとフーリエは同じ頃に活躍した人物であるが,ラプラス変換が 1780年頃,フーリエ変換が 1807年頃の発表であり,両者の発想にそれほど深い関わりはないように思われる。
実際にラプラス変換を世に広まったのは交流電気が登場した時代、それも「稀代の叩き上げ電気技師」オリヴァー・ヘヴィサイド(Oliver Heaviside,1850年~1925年)による功績が大きかったのです。
ラジオと電気回路と三角関数
その特徴をフーリエ変換に対応させる形で列記してみましょう。
【Python演算処理】ラプラス変換/ラプラス逆変換を試す。
線形性
\mathcal{L}[af(t)+bg(t)] = a\mathcal{L}[f(t)] + b\mathcal{L}[g(t)]
相似定理
\mathcal{L}[f(at)]→\frac{1}{a} F(\frac{s}{a}) (a>0)\\
\mathcal{L}[(\frac{1}{a} f(\frac{t}{a})] → F(as) (a>0)\\
\mathcal{L}^-1[F(as)]→\frac{1}{a} f(\frac{t}{a})(a>0)\\
\mathcal{L}^-1[(\frac{1}{a} F(\frac{s}{a})] → f(as)(a>0)
推移則
\mathcal{L}[e^{at} f(t)] → F(s-a)
微分則
\mathcal{L}[\frac{df(t)}{dt}] → sF(s)-f(0)\\
\mathcal{L}[\frac{d^n f(t)}{dt^n}] → s^n F(s)-s^{n-1} -…-sf^{n-2} (0)-sf^{n-1}(0)
積分則
\mathcal{L}(\int_{0}^{t} f(x)ds)=\frac{1}{s}\mathcal{L}(f)\\
\mathcal{L}[\int_{0}^{t} \int_{0}^{t} \int_{0}^{t} … \int_{0}^{t} f(t)(dt)^n] → \frac{1}{s^n} F(s) + \frac{1}{s^n} f^{-1}(0)+…+\frac{1}{s} f^{-n}(0)
しかし実はフーリエ変換とラプラス変換の間には、さらなる発想の飛躍が存在するのです。
実数列(Real Sequance)からの時間軸(Time Axis)の抽出と「状態遷移」なる新概念導入。
ところでフーリエ級数については冪乗算$e^n$を元とするネイピア族に単純に下族するのではなく、冪乗算$e^{θi}$を元とする別の族とする考え方があります。
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」?
- これを「フーリエ族」と呼び分ける事にした場合、離散フーリエ変換(DFT)の演算結果集合がそれに完全に下属するのに対し、フーリエ変換/逆変換のそれは無限周期波形や畳み込み積などにおいて閉じてない。
- ラプラス変換/逆変換に至っては「任意の回路方程式」なる全く異なる演算結果集合を元とする別物としか考えられない。どうやらこれはこれで「ラプラス族」なる別の族を立てる必要が生じる様である。
その一方で離散フーリエ変換(DFT)やラプラス変換/逆変換においては、明示的に実数列(Real Sequance)からの時間軸(Time Axis)の抽出が為されている事に注目せざるを得ません。これはそれまで数学史上ではあくまで黙殺されてきた因子です。
【初心者向け】線形関数や絶対値関数
単純に物理学の世界から導入したと考えるだけでなく、リアルタイム処理ではAD変換やDA変換に伴う遅延時間なども意識せざるを得なくなってきた事を考慮に入れるべきかもしれません。
しかも(ここでいう「ラプラス族」が元とする)回路方程式の演算結果集合は、さらに異なる時間概念を内包しているのです。
回路方程式は、回路の状態変化があった後の回路構成、例えばスイッチを閉じた後の電流変化の様子、すなわち過渡状態を経て定常状態に落ち着く様子を定係数線形微分方程式で表します。
その一般解は、=0とおいた同次微分方程式の一般解を$y_t$、≠0の非同次微分方程式の特殊解を$y_s$とすると、次のようになります。
$y=y_t+y_s$
$y_t$は回路に抵抗がある場合には、過渡状態を経て定常状態に落ち着いた時点で必ず0となるので$y_s$は定常状態における値となります。よって、過渡現象においては$y_t$を過渡解、$y_s$を定常解といいます。
この関係を整理すると、次のようになります。
過渡状態=定常解(非同次方程式の特殊解)+過渡解(同次方程式の一般解)
定常状態=定常解(非同次方程式の特殊解)
コンピューターでいうと以下の様な時間区分で推移する訳ですね。
- 【過渡状態】起動シークエンス(電源がOnになってからOSのカーネルメインループがイベント待ち状態に入るまで)。
- 【定常状態】イベント待ち状態(イベント待ち状態で回ってるループは、カーネルメインループだけとは限らない)。
- 【過渡状態】イベント処理が始まり、それが終了するまで。
これに「(機械学習の結果などに基づく)活性化関数による状態遷移」の概念を加えると、ある種の系として完全に閉じた情報処理システムが浮かび上がってくる様です。もしかしたらこういう考え方こそが(ともすれば時間概念を黙殺しようとする数学の世界も座視してはいられなくなった筈の)人工知能概念の大源流たるべきなのかもしれません。
AI(人工知能)や機械学習に必要な数学のレベルと勉強方法を5分で解説!
上掲の「完全に閉じたシステムとは何か?」という観点に到達するまでは、私も以下の様に捉えていました。
数学に、時間の概念は必要でしょうか?
時間とは何かという問題は主に物理的・哲学的問題であって、数学は直接には関わらないように思いますが、熱力学や統計力学などのエントロピー増大の法則や最も美しい法則といわれる熱力学第二法則は時間の矢と直接関係しますので、熱にかかわる問題を数学的に考えようというときは積極的に数学にも時間の考えが現れます。
熱伝導方程式のようなもろに時間と関わる方程式や、リッチフローもこの種の方程式であるので時間が数式に直接関わるのです。
リッチフロー - Wikipedia時間とは何かという問題は非常に難しいため、長きにわたって人類の謎とされてきたのですが、アインシュタインはそのタブーに迫りました。彼の考え方によると空間と時間は無関係どころか直接強い関わりがあるということです。元々ブラウン運動という熱の運動とランダムの考察をしていたのですが、これは量子力学への道を開きながらもアインシュタイン自身はこれを嫌ったといいます。
しかしまた一方では時間と空間が直接美しく関係する相対性理論をも生み出しました。熱力学・とくに第二法則という時間が直接かかわる物理法則と、電磁気・光速度不変性から導かれた時間への革命的考察が、量子論と相対論という何か相反するように見える形で時間に関する深い考察を生み、彼を統一理論への夢へ向かわせたと考えられます。
上掲の「人工知能概念の大源流」概念は、こうした考察にさらに新たな検討材料を提供する様です? そんな感じで以下続報…