1.はじめに
1.1 記事の内容
この記事は,離散フーリエ変換(Discrete Fourier Transform, DFT)の 原理・公式導出をできるだけ分かりやすく・簡単な表記・記号・図や実例などで解説することを目的としています.
離散フーリエ変換とは,離散的な信号を三角関数の和に分解する変換です.離散的な信号とは,「$n$次元ベクトル」や「要素数$n$の配列」とも言いかえることができます.
これらのデータはいかなる実数・複素数値を取るデータだとしても $n$ 個の $\sin$と$\cos$ に分解できることが知られています.分解された $\cos, \sin$ の成分量だけに注目すると,$2n$ 個の実数配列,あるいは 長さ $n$ の複素ベクトル(複素数の配列)に変換できます.
つまり 離散フーリエ変換 とは,長さ $n$ の実数ベクトル(配列)を入力に,長さ $n$ の複素ベクトル(配列)を出力する変換と言えます.(一般化により,長さ $n$ の複素ベクトルを入力に,長さ $n$ の複素ベクトルを出力する操作とも言えます)
離散フーリエ変換を高速に行うアルゴリズムのことを 高速フーリエ変換(Fast Fourier Transform, FFT) と言います.
離散フーリエ変換により複数の$\sin, \cos$ 波に分解することができるので,ある音声データに含まれる音の周波数を分析することなどが可能です.
また,離散フーリエ変換の公式が持つ副作用的な特徴により,畳み込み(合成積) を求めることができます.畳み込みは
- 音声信号処理における「エコー」「リバーブ」フィルタ
- 画像信号処理における「ブラー(ぼかし)」「シャープ化」フィルタ
- 競技プログラミングにおける畳み込み演算のアレコレ(e.g. 多倍長整数の掛け算.多項式の掛け算.組み合わせ)
などの幅広い用途で使われます.畳み込みはナイーブな実装だとサイズ$n$ のデータに対して $O(n^2)$ の計算時間がかかりますが,FFT を用いることで $O(n \log n)$ で計算できるようになります.とっても速いですね.
(畳み込みを考えるときは,周波数成分の分解というDFTの本来の目的・特徴はあまり重要ではありません)
DFT の公式を既知として FFT の解説を行う記事は割とたくさんある気がするのですが,FFT未履修者にとって DFT の複雑な公式をいきなり出されても数式拒否してしまう事もあると思ったので,DFT を詳しく解説する記事を書きました.
この記事では
- 事前に必要となる知識の説明(2章,3章)
- 離散信号から周波数成分を分解する方法(4章)
- 周波数成分の情報があるとき,元の離散信号に戻す方法(5章)
- 一般的な離散フーリエ変換公式への整形(6章)
- 離散フーリエ変換にまつわる補助知識・Tips(7章)
の順番で説明します.
1.2 前提知識
高校2年生程度でも分かるぐらいを目指して書いています.しかし高度な高校数学は使わないので,数学の断片的な知識があれば中学生でも分かると思います.
以下,知っていると嬉しいことをリストします.
-
sin,cos 関数の形
数学II の範囲ですが,$\sin(45^o), \cos(210^o)$ などの値が分かる程度の理解度で大丈夫です.覚えていなくても適宜グラフを読めば分かると思います. -
ベクトル・行列・行列とベクトルの掛け算 (参考: wikibooks・ヨビノリ)
ベクトルは数学B,行列は大学数学(旧数C)の範囲ですが,方程式などを簡単に記述するために使うのがメインです.固有値計算など高度な行列の知識は 必要ありません .
例えば行列とベクトルの掛け算は $\left(\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right)
\left(\begin{matrix}x\\y\\z\end{matrix}\right) = \left(\begin{matrix}ax+by+cz\\dx+ey+fz\\gx+hy+iz\end{matrix}\right)$ の様に計算できます
途中で出てくる行列・ベクトルの転置 $(^\top)$ は縦と横を入れ替えるものです.説明のスペースの都合などで縦横を変えて表記することがあります.例えば $(1\ 2\ 3)^\top = \left(\begin{matrix}1\\2\\3\end{matrix}\right)$ です. -
総和記号 $\sum$
例えば
$$\sum\limits_{k=1}^{4}(k+1)(k-5) = (\color{#c00}{1}+1)(\color{#c00}{1}-5)+(\color{#c00}{2}+1)(\color{#c00}{2}-5)+(\color{#c00}{3}+1)(\color{#c00}{3}-5)+(\color{#c00}{4}+1)(\color{#c00}{4}-5)$$
です.高度な変形公式などは要りません. -
複素数 $i$, 複素数平面
一応数III ですが,いわゆる $i = \sqrt{-1}$ を知ってればだいたい大丈夫です.🤔
未履修な方はこのYouTube動画あたりがおすすめです. -
表記について
- 行列は $\pmb{W}, \pmb{C}$ の様に太字の大文字で表記します.
- ベクトルは $X$ の様に大文字で表記します.
- スカラ値(行列でもベクトルでもない要素1の普通の値)は $a$ の様に小文字で表記します.
- $\mathbb{R}$は実数を,$\mathbb{C}$は複素数を,$\mathbb{R}^n$ は長さ$n$ の実数ベクトル(プログラミングで言う配列)を示します.
- 円の1周の角度を$360^o$とする度数法をメインにつかいます.$2\pi$ とする弧度法(ラジアン)は基本使いません
- $\omega, \zeta$ などの馴染みの低そうなギリシャ文字は極力使わず,ラテンアルファベットをメインに解説します.他の解説と使っている文字が違うかもしれませんが,本質は一緒です.
1.3 フーリエ変換などとの違い
文脈などによっては フーリエ変換 と言って 高速フーリエ変換(FFT) や 離散フーリエ変換(DFT) の事を指すことがありますが,純粋な フーリエ変換 は FFT とも DFT とも違う計算を指します(原理は似てはいますが).
フーリエ変換と名前に付く,似た変換は以下の4種類があります.
| 時間領域 | 名前 | 周波数領域 | ||
|---|---|---|---|---|
| 連続 | 周期的 | フーリエ級数展開 | 離散的 | 非周期的 |
| 連続 | 非周期的 | フーリエ変換 | 連続 | 非周期的 |
| 離散的 | 非周期的 | 離散時間フーリエ変換 | 連続 | 周期的 |
| 離散的 | 周期的 | 離散フーリエ変換 | 離散的 | 周期的 |
周波数領域とか,周期的・非周期的 とか良く分かりませんね.
今は分からなくてもいいですが,このような特性の違う変換があるということを覚えておけば良いです.
フーリエ級数展開から説明をするのが一般な気がしますが,今回は直接離散フーリエ変換の解説をします.(個人的にはフーリエ級数展開よりも離散フーリエ変換の方が理解しやすいと思います)
2.直交基底
なんてことはない,すぐに $\left(\begin{matrix}x\\y\end{matrix}\right) = \left(\begin{matrix}4\\7\end{matrix}\right)$ と答えられるでしょう.
しかし,グラフの端に書かれている軸が $x, y$ 軸とは明示されていないため,ひねくれた座標系のとり方をすると $\left(\begin{matrix}x\\y\end{matrix}\right) = \left(\begin{matrix}3\\2\end{matrix}\right)$ も正解になります.
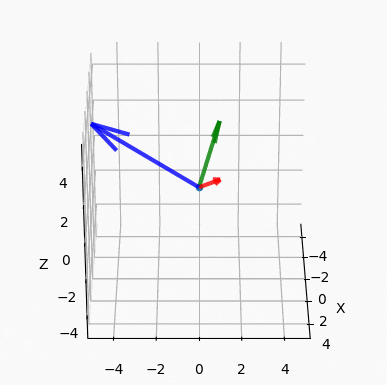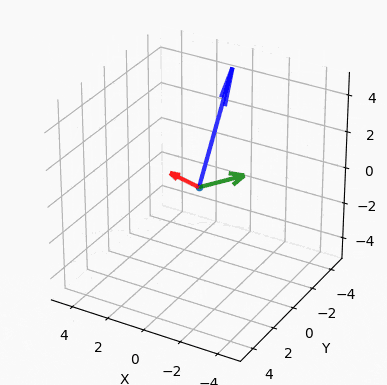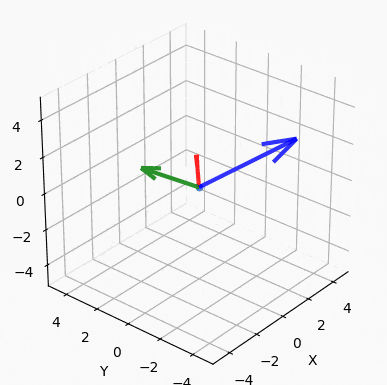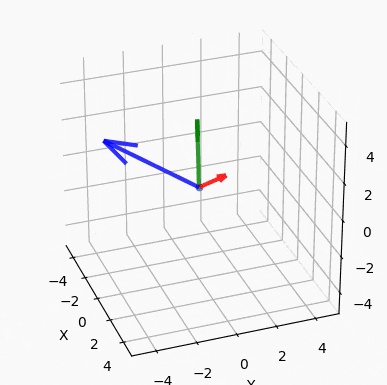
前者は基底として,グリッドの座標で言う $\left(\begin{matrix}1\\0\end{matrix}\right), \left(\begin{matrix}0\\1\end{matrix}\right)$ の2つのベクトルを,後者は $\left(\begin{matrix}2\\1\end{matrix}\right), \left(\begin{matrix}-1\\2\end{matrix}\right)$ の2つを用いて表現した座標系です.図示すると以下のようになります.
赤い矢印が x 軸の 1 単位,青い矢印が y 軸の 1 単位と言われると,左は $\left(\begin{matrix}4\\7\end{matrix}\right)$,右は $\left(\begin{matrix}3\\2\end{matrix}\right)$ であることに納得いただけるでしょう(?)
零ベクトルで無く,互いに平行では無い2次元基底ベクトルを2つ用意することにより,2次元平面上の全ての点をこの2つの基底ベクトルを用いて表現することが可能です.
またこの2つの基底が直交,つまり 90度で交わるとき,直交基底と呼びます.ベクトルが直交しているかどうかは内積(要素ごとの積の和)が0であるかどうかで確認することができます.
これはベクトル$A$, $B$ の内積 $A \cdot B$ は $\Vert A\Vert\Vert B\Vert \cos\theta$ と書き換えることができ,$A$, $B$の交わる角度 $\theta$ が $90^o$ のとき,$\cos(90^o) = 0$であることからも分かります.
先に示した2種類の基底は直交基底になります.また,ベクトル $\left(\begin{matrix}\cos(18^o)\\\sin(18^o)\end{matrix}\right)$ とそれを $90^o$ 回転させた $\left(\begin{matrix} \cos(18^o+90^o)\\\sin(18^o+90^o)\end{matrix}\right)$ の組なども直交基底になります.実際に確かめると,
$$
\left(\begin{matrix}1\\0\end{matrix}\right) \cdot \left(\begin{matrix} 0\\1\end{matrix}\right) = 1 \times0 + 0\times1 = 0
$$
$$
\left(\begin{matrix}2\\1\end{matrix}\right) \cdot \left(\begin{matrix}-1\\2\end{matrix}\right) = 2 \times(-1) + 1\times2 = 0
$$
$$
\left(\begin{matrix}\cos(18^o)\\\sin(18^o)\end{matrix}\right) \cdot \left(\begin{matrix} \cos(18^o+90^o)\\\sin(18^o+90^o)\end{matrix}\right) =
\left(\begin{matrix}\cos(18^o)\\\sin(18^o)\end{matrix}\right) \cdot \left(\begin{matrix} -\sin(18^o)\\\cos(18^o)\end{matrix}\right) =
\cos(18^o) \times {-\sin(18^o)} + \sin(18^o) \times \cos(18^o) = 0
$$
確かに基底ベクトル同士の内積は 0 になります.(※三角関数の還元公式)
直交基底を用いると,点の位置ベクトル $P$ と基底ベクトル$A$ の内積を求めることによって,基底ベクトルをどれほど含むかが分かります.具体的には
$$
\bbox[#ded,20px]{\frac{P\cdot A}{\Vert A\Vert ^2} = \frac{P\cdot A}{A \cdot A}}
$$
を求めれば良いです.( 正射影 )
実際,
$$
\frac{\left(\begin{matrix}4\\7\end{matrix}\right) \cdot \left(\begin{matrix} 1\\0\end{matrix}\right)}
{\left\Vert \left(\begin{matrix} 1\\0\end{matrix}\right)\right\Vert ^2} = \frac{4}{1} = 4,
\frac{\left(\begin{matrix}4\\7\end{matrix}\right) \cdot \left(\begin{matrix} 0\\1\end{matrix}\right)}
{\left\Vert \left(\begin{matrix} 1\\0\end{matrix}\right)\right\Vert ^2} = \frac{7}{1} = 7
$$
$$
\frac{\left(\begin{matrix}4\\7\end{matrix}\right) \cdot \left(\begin{matrix} 2\\1\end{matrix}\right)}
{\left\Vert \left(\begin{matrix} 2\\1\end{matrix}\right)\right\Vert ^2} = \frac{15}{5} = 3,
\frac{\left(\begin{matrix}4\\7\end{matrix}\right) \cdot \left(\begin{matrix} -1\\2\end{matrix}\right)}
{\left\Vert \left(\begin{matrix} -1\\2\end{matrix}\right)\right\Vert ^2} = \frac{10}{5} = 2
$$
と抽出できていることが分かります.
これは高次元でも適応できます.例えば3次元の基底ベクトルとして
$$
A=\left(\begin{matrix} 1\\ 1\\1\end{matrix}\right),
B=\left(\begin{matrix} 1\\-5\\4\end{matrix}\right),
C=\left(\begin{matrix}-3\\ 1\\2\end{matrix}\right),
$$
の3つを用意します.$A\cdot B = A\cdot C = B\cdot C = 0$ であることが確かめられるので,この3本のベクトルは直交します.図で示すと以下のとおりです.
ここで点$P = 7A-3B+5C = (-11, 27, 5)^\top$ を用意します.このベクトル $P$ を$A, B, C$ に分解してみましょう.
$$\frac{P \cdot A}{\left\Vert A\right\Vert ^2} = \frac{-11+27+5}{3} = 7$$
$$\frac{P \cdot B}{\left\Vert B\right\Vert ^2} = \frac{-11-135+20}{42} = -3$$
$$\frac{P \cdot C}{\left\Vert C\right\Vert ^2} = \frac{33+27+10}{14} = 5$$
無事に 3 成分に分解することができました!
3.離散系での三角関数
三角関数って知ってますか? 私は知っています.
離散フーリエ変換では(時間的に)周期的なデータを入力として扱います.
周期的とは同じ波・信号データが変わらずに繰り返しているものを指します.非周期的っぽい適当なデータの場合でも適応できるのですが,その話はあとでします.
今回登場するのは三角関数の中でも $\sin$ と $\cos$ です.一般的な $\sin(\theta)$ と $\cos(\theta)$ として,以下のグラフを想像すると思います.
$\sin$ と $\cos$ は $360^o$ 毎に値を繰り返す,(時間的に)周期的な関数です.
しかし,今回扱うのは離散系での三角関数です.通常の数学では $\sin(\theta)$ は連続な関数なので,$\theta$ にどんなに細かい値を代入しても対応する $\sin(\theta)$ の値が得られます.例えば音叉を叩いたとき,空気中を伝わる波は連続的な $\sin$ 波になります.(連続時間信号)
ですが,その音を録音しコンピューターで扱うときは,飛び飛びの離散的なデータとして扱われます.(離散時間信号)
連続的な信号から離散的な信号を作り出すことを標本化(サンプリング)と呼びます.
これで1.3で紹介した表の 時間領域 で 連続的・非連続的・周期的・非周期的 について説明しました.
さて,上の $\cos$ と $\sin$ の1周期分(水色の部分)をサンプル数 $n = 8$ として標本化すると以下のようになります.
8個の点が 45° ごとに標本化されています.
$\cos(\theta)$ ではなく $\cos[\theta]$ と角括弧を使っているのは,関数の引数が離散的な値であることを示しています.教科書などでは角括弧の中は整数のときに使うことが多いのですが,今回はゆるふわ解説なので離散的なときに使います.
$\cos$ 関数の周波数(1単位時間で波打つ回数.[Hz])を変化させて, $n = 8$ で標本化したものは以下のようになります.
Python3 によるソースコード
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0, 1, 1/1000)
xd = np.arange(0, 1, 1/8)
fig = plt.figure(figsize=(10, 11))
fig.subplots_adjust(wspace=0.1)
for i in range(12):
sub = fig.add_subplot(3, 4, i+1)
sub.set_title(str(i) + r"Hz Cos")
sub.set_xticks(np.linspace(0, 1, 4+1))
sub.set_xticks(np.linspace(0, 1, 8+1), minor=True)
sub.set_xticklabels([str(2*v)+"/8" for v in range(0, 4+1)])
sub.set_yticks(np.linspace(-1, 1, 4+1))
sub.set_yticks(np.linspace(-1, 1, 20+1), minor=True)
sub.set_ylim(-1.1, 1.1)
sub.set_yticklabels([])
sub.grid(b=True, which='minor', color='0.85')
sub.grid(b=True, which='major', color='0.65')
sub.plot(x, np.cos(i * x * 2*np.pi), linewidth = 0.7)
sub.plot(xd, np.cos(i * xd* 2*np.pi), color="b", marker="o", linestyle="")
plt.show()
plt.savefig("fig2-3.svg")
0 Hz の波とは,$cos(0) = 1$ のまま,全く振動しない波です(?).
離散化された青い点のみに注目すると,0 Hzと8 Hzの波,1 Hz と 9 Hz の波,…と $a$ Hz と $a+n$ Hz の波が同じ形になっていることが分かります.
このように離散系の波の周波数成分は $a, a+n, a+2n, a+3n, ...$ [Hz] で同じ値が繰り返される周波数領域での周期性があります.
また,周波数は 1 Hz, 2 Hz の様に,離散的であり,1.5 Hz のような中途半端な周波数は使いません.これは単位時間内で周期的である必要があるので,単位時間内にピッタリ収まる波でないといけないからです.
これが1.3で紹介した表の 周波数領域 で 連続的・非連続的・周期的・非周期的 についての説明です.
更に観察すると,1 Hz と 7 Hz の波,2 Hz と 6 Hz の波,3 Hz と 5 Hz の波と…のように,$a$ Hz と $n-a$ Hz の波も同形です.
分かりやすくグラフを抜粋して重ねると,以下のようになります.
連続的な波形は違う形ですが,周波数によっては離散化によって同じ形になることがあります.
ヘリコプターの回転する羽をビデオで撮影するとき,目で見ると回転して見えるのに回転速度とシャッター速度の条件が揃うと動画では羽が回ってないように見える現象に似てますね.
次に $\sin$ 関数の周波数を変化させて, $n = 8$ で標本化したものは以下のようになります.
$n$ Hz 以上の波に関して,離散 $\cos$ 波と同様に $a$ Hz と $a+n$ Hz が同形なので省略します.
離散 $\sin$ 波の場合,1 Hz と 7 Hz の波が正負が逆の関係になっています.同様に2 Hz と 6 Hz の波,3 Hz と 5 Hz の波,…と $a$ Hz と $n-a$ Hz の波は正負を反転させて同形になっています.
このように離散系の場合,サンプリング周波数(単位時間あたりのサンプル数)を $n$ [Hz] としたとき,$n/2$ [Hz] 以上の高周波数の波は,低周波数の波と見分けがつかなくなります.この周波数 $n/2$ [Hz]を ナイキスト周波数 と呼びます.
逆に言うと,波形の最大周波数を $f$ としたとき,$2f$ [Hz] を超えた周波数で標本化すれば,元の波形を完全に再現することができます.
例えば音楽CDなどではサンプリング周波数 44,100Hz で標本化されているので,22,050Hz の音まで再現できます.収録の際には 20 kHz前後以上の音が混じらないようにローパスフィルタでカットされます.
人の可聴域の上限は 20kHz 程度なので,このサンプリング数であれば人間に聞こえる音は全て記録できる事になります.
4.周波数の抽出
手元にある信号データがあったとして,それがどんな周波数の波なのか,どんな周波数成分を含むのか知りたいときがあります.ここでは周波数成分の抽出について考えます.
まず,サンプル数 $n=8$ で周波数 $f$ [Hz] の離散コサインの値を表すベクトル $C_f$ を用意します.$C_f[a] = \cos\left(\frac{360^o}{n}af\right)$ です.
正負を分かりやすくするため,正を赤,負を青のグラデーションで表現しています.
$$
\begin{matrix}
C_0 = (& \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} &)\\
\
C_1 = (& \color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} &)\\
\
C_2 = (& \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} &)\\
\
C_3 = (& \color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} &)\\
\
C_4 = (& \color{#f00}{ 1} & \color{#00f}{-1} & \color{#f00}{ 1} & \color{#00f}{-1} & \color{#f00}{ 1} & \color{#00f}{-1} & \color{#f00}{ 1} & \color{#00f}{-1} &)\\
\
C_5 = (& \color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} &)\\
\
C_6 = (& \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} &)\\
\
C_7 = (& \color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} &)
\end{matrix}
$$
です.$C_3$のときの値をWolframAlphaで計算したものはこちら.
同様に,周波数 $f$ [Hz] の離散サインべクトルを $S_f$ と表します.
$$
\begin{matrix}
S_0 = (& \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} &)\\
\
S_1 = (& \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} &)\\
\
S_2 = (& \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} &)\\
\
S_3 = (& \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} &)\\
\
S_4 = (& \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} &)\\
\
S_5 = (& \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} &)\\
\
S_6 = (& \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} &)\\
\
S_7 = (& \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} &)\\
\end{matrix}
$$
ここで,2つのベクトルの内積を取ってみたいと思います.
それぞれのベクトル同士の内積を計算したものは以下の通りになります.
| $\mathrm{dot}$ | $C_0$ | $C_1$ | $C_2$ | $C_3$ | $C_4$ | $C_5$ | $C_6$ | $C_7$ |
|---|---|---|---|---|---|---|---|---|
| $C_0$ | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $C_1$ | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 4 |
| $C_2$ | 0 | 0 | 4 | 0 | 0 | 0 | 4 | 0 |
| $C_3$ | 0 | 0 | 0 | 4 | 0 | 4 | 0 | 0 |
| $C_4$ | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 |
| $C_5$ | 0 | 0 | 0 | 4 | 0 | 4 | 0 | 0 |
| $C_6$ | 0 | 0 | 4 | 0 | 0 | 0 | 4 | 0 |
| $C_7$ | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 4 |
| $\mathrm{dot}$ | $S_0$ | $S_1$ | $S_2$ | $S_3$ | $S_4$ | $S_5$ | $S_6$ | $S_7$ |
|---|---|---|---|---|---|---|---|---|
| $S_0$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $S_1$ | 0 | 4 | 0 | 0 | 0 | 0 | 0 | -4 |
| $S_2$ | 0 | 0 | 4 | 0 | 0 | 0 | -4 | 0 |
| $S_3$ | 0 | 0 | 0 | 4 | 0 | -4 | 0 | 0 |
| $S_4$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $S_5$ | 0 | 0 | 0 | -4 | 0 | 4 | 0 | 0 |
| $S_6$ | 0 | 0 | -4 | 0 | 0 | 0 | 4 | 0 |
| $S_7$ | 0 | -4 | 0 | 0 | 0 | 0 | 0 | 4 |
| $\mathrm{dot}$ | $C_0$ | $C_1$ | $C_2$ | $C_3$ | $C_4$ | $C_5$ | $C_6$ | $C_7$ |
|---|---|---|---|---|---|---|---|---|
| $S_0$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $S_1$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $S_2$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $S_3$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
$C_3 \cdot C_3$ を WolframAlphaで計算した結果はこちら.
零ベクトルである $S_0, S_4$ を除いて,内積が非0になるのは同じベクトル同士のときだけです.
奇関数である $\sin$ と偶関数である $\cos$ を掛けたものは奇関数になるので,その総和は 0 になります.(偶関数と奇関数の意味)
$\cos$ 同士,$\sin$ 同士をかけ合わせたものは偶関数になるのですが,周期が違うものの内積は 0 になる性質があります.
これは積和の公式
$$
\begin{matrix}
\cos(a)\cos(b) = \dfrac{\cos(a+b)+\cos(a-b) }{2} \\
\sin(a)\sin(b) = \dfrac{-\cos(a+b)+\cos(a-b)}{2}
\end{matrix}
$$
を用いて証明することができます.
$\cos$ 同士のときの場合を説明します.$\sin$ 同士のときも同様の手順で説明できます.
$$
\begin{matrix}
\sum\limits_{k=0}^{n-1}\cos\left(\dfrac{360^o}{n}ak\right)\cos\left(\dfrac{360^o}{n}bk\right)\\
=\sum\limits_{k=0}^{n-1}\dfrac{1}{2}\left\{\cos{\left(\dfrac{360^o}{n}(a+b)k\right)}+\cos{\left(\dfrac{360^o}{n}(a-b)k\right)}\right\}\\
=\dfrac{1}{2}\sum\limits_{k=0}^{n-1}\cos{\left(\dfrac{360^o}{n}(a+b)k\right)} +
\dfrac{1}{2}\sum\limits_{k=0}^{n-1}\cos{\left(\dfrac{360^o}{n}(a-b)k\right)}
\end{matrix}
$$
が,$a\equiv\pm b \pmod{n}$ のとき非0,それ以外では0を示せれば良いです.
前半の $\dfrac{1}{2}\sum\limits_{k=0}^{n-1}\cos{\left(\dfrac{360^o}{n}(a+b)k\right)}$ について,$a\equiv -b \pmod{n}$ のときは $\cos$ の中が $360^o$ の倍数(0も含む)になるので,
$$
\dfrac{1}{2}\sum\limits_{k=0}^{n-1}\cos{\left(\dfrac{360^o}{n}(a+b)k\right)} = \dfrac{1}{2}\sum\limits_{k=0}^{n-1}\cos(0) = \dfrac{n}{2}
$$
になります.それ以外のときは非0になります.厳密な証明は複素数を用いた証明になり難しいですが,イメージとしては複素数平面上にプロットしたときに多角形の頂点として構成され,その頂点座標の合計=$n\times$平均=$n\times$多角形の重心 は原点になるので,0になります.(参考:1のn乗根の和)
後半の $\dfrac{1}{2}\sum\limits_{k=0}^{n-1}\cos{\left(\dfrac{360^o}{n}(a-b)k\right)}$ について,同様の手順で $a\equiv b \pmod{n}$ のときは $\frac{n}{2}$,それ以外のときは0になることが分かります.
以下,いくつかのベクトル対の内積の様子を図示したものになります.
2つのベクトルを赤・青のグラフで,その積を黄色のグラフで示しています.黄色の棒グラフは離散部分の積を示し,この合計が内積です.
$x=0, 4$ の軸を太線にしたので,関数の偶関数性・奇関数性を感じ取るのに役立ててください.
Python3 によるソースコード
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0, 8, 1/256)
xd = x[0: 256*8: 256]
def plot(title, sub, a, b, lim=1):
ad = a[0: 256*8: 256]
bd = b[0: 256*8: 256]
ab_dot = np.dot(ad,bd)
sub.set_title(title + " ={:4.2f}".format((0 if abs(ab_dot) < 0.01 else ab_dot)))
sub.set_xticks(np.linspace(0, 8, 8+1))
sub.set_xticklabels(range(8))
sub.set_xlim(-0.5, 8.0)
sub.text(7.5, -1.19*lim, r"$\times\frac{360^o}{8}$")
sub.set_yticks(np.linspace(-1*lim, 1*lim, lim*4+1))
sub.set_yticks(np.linspace(-1*lim, 1*lim, lim*20+1), minor=True)
sub.set_ylim(-lim*1.03, lim*1.03)
sub.grid(axis='x', b=True, which='major', color='0.85')
#sub.grid(axis='y', b=True, which='minor', color='0.85')
sub.grid(axis='y', b=True, which='major', color='0.6')
sub.vlines([0,4], -lim-0.1, lim+0.1, color='0.2')
# sub.fill_between(x, a, alpha=0.08, color="blue" )
# sub.fill_between(x, b, alpha=0.08, color="orangered")
# sub.bar( xd, bd, alpha=0.5, color="orangered", width=1/8)
# sub.bar( xd, ad, alpha=0.5, color="blue", width=1/8)
# sub.plot(xd, ad, alpha=0.5, color="blue", marker="x", markersize=10, markeredgewidth=3, linestyle="")
# sub.plot(xd, bd, alpha=0.5, color="orangered", marker="x", markersize=10, markeredgewidth=3, linestyle="")
# sub.bar( xd, ad*bd, alpha=0.6, color="gold", width=0.7)
sub.plot(x, a, alpha=0.5, color="orangered", linewidth=1)
sub.plot(x, b, alpha=0.5, color="blue", linewidth=1)
sub.plot(x, a*b, alpha=0.7, color="gold", linewidth=2)
sub.bar(xd, ad*bd, alpha=1, color="goldenrod", width=0.3, edgecolor='0.2', linewidth=2.0)
fig = plt.figure(figsize=(10, 12))
fig.subplots_adjust(wspace=0.18)
plot(r"$\cos[ \theta]\cdot \cos[ \theta]$", fig.add_subplot(3, 3, 1), np.cos(1 * x/4* np.pi), np.cos(1 * x/4* np.pi))
plot(r"$\cos[ \theta]\cdot \cos[2\theta]$", fig.add_subplot(3, 3, 2), np.cos(1 * x/4* np.pi), np.cos(2 * x/4* np.pi))
plot(r"$\cos[ \theta]\cdot \cos[3\theta]$", fig.add_subplot(3, 3, 3), np.cos(1 * x/4* np.pi), np.cos(3 * x/4* np.pi))
plot(r"$\cos[ \theta]\cdot \cos[4\theta]$", fig.add_subplot(3, 3, 4), np.cos(1 * x/4* np.pi), np.cos(4 * x/4* np.pi))
plot(r"$\cos[3\theta]\cdot \cos[4\theta]$", fig.add_subplot(3, 3, 5), np.cos(3 * x/4* np.pi), np.cos(4 * x/4* np.pi))
plot(r"$\cos[0 )\cdot \cos[ \theta]$", fig.add_subplot(3, 3, 6), np.cos(0 * x/4* np.pi), np.cos(1 * x/4* np.pi))
plot(r"$\sin[ \theta]\cdot \sin[2\theta]$", fig.add_subplot(3, 3, 7), np.sin(1 * x/4* np.pi), np.sin(2 * x/4* np.pi))
plot(r"$\sin[ \theta]\cdot \cos[ \theta]$", fig.add_subplot(3, 3, 8), np.sin(1 * x/4* np.pi), np.cos(1 * x/4* np.pi))
plot(r"$\sin[ \theta]\cdot \cos[2\theta]$", fig.add_subplot(3, 3, 9), np.sin(1 * x/4* np.pi), np.cos(2 * x/4* np.pi))
plt.show()
plt.savefig("fig2-5.svg")
内積が0になるということはそれらのベクトルは直交していることになります.
零ベクトルでなく互いに内積が 0 になるのは $C_0, C_1, C_2, C_3, C_4, S_1, S_2, S_3$ の8つの組です.
サンプル数 $n = 8$ であったので入力信号ベクトルは 8 次元ベクトルであり,直交基底ベクトルが 8 つあるので,どんな入力信号に対しても,この 8 つのベクトルで表現できることが分かります.実際に分解して試してみましょう.
$$g[\theta] = 2\cos(2\theta) - \cos(3\theta) + \frac{1}{4}\sin(3\theta)$$
という関数を考えます.
この1周期分を $n = 8$ でサンプリングすると以下のようになります.
$$
\begin{matrix}
G=2C_2-C_3+\frac{1}{4}S_3=(\color{#f00}{ 1.00} & \color{#e00}{ 0.88} & \color{#00f}{-2.25} & \color{#00a}{-0.53} & \color{#f00}{ 3.00} & \color{#00e}{-0.88} & \color{#00f}{-1.75} & \color{#a00}{ 0.53})
\end{matrix}
$$
これを各 $C_i$, $S_i$ との内積を計算すると以下のようになります.
| $i$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| $C_i$ | 0 | 0 | 8 | -4 | 0 | -4 | 8 | 0 |
| $S_i$ | 0 | 0 | 0 | 1 | 0 | -1 | 0 | 0 |
$$\frac{G \cdot C_2}{\left\Vert C_2\right\Vert ^2} = \frac{8}{4} = 2$$
$$\frac{G \cdot C_3}{\left\Vert C_3\right\Vert ^2} = \frac{-4}{4} = -1$$
$$\frac{G \cdot S_3}{\left\Vert S_3\right\Vert ^2} = \frac{1}{4} $$
と各成分に分解できていることが分かります.
それでは次に,位相がズレている波はどうなるのでしょう.$\sin(\theta + 60^o)$ について考えます.
位相がズレた波に関しても,三角関数の合成公式の逆を使って,$\sin$ と $\cos$ に分解することができます.この例では,
$$\sin(\theta + 60^o) = \frac{1}{2}\sin(\theta) + \frac{\sqrt{3}}{2}\cos(\theta)$$
と分解することができます.(WolframAlpha)
実際にこの波1周期分をサンプリングすると
$$
\begin{matrix}
(\color{#d00}{ \frac{\sqrt{3}}{2}} & \color{#e00}{ \frac{\sqrt{6}+\sqrt{2}}{4}} & \color{#a00}{ \frac{1}{2}} & \color{#007}{-\frac{\sqrt{6}-\sqrt{2}}{4}} & \color{#00d}{-\frac{\sqrt{3}}{2}} & \color{#00e}{-\frac{\sqrt{6}+\sqrt{2}}{4}} & \color{#00a}{-\frac{1}{2}} & \color{#700}{ \frac{\sqrt{6}-\sqrt{2}}{4}})\\
\
\simeq(\color{#d00}{ 0.866} & \color{#e00}{ 0.966} & \color{#a00}{ 0.500} & \color{#007}{-0.259} & \color{#00d}{-0.866} & \color{#00e}{-0.966} & \color{#00a}{-0.500} & \color{#700}{ 0.259})\\
\end{matrix}
$$
となり,これを各 $C_i$, $S_i$ との内積を計算すると
| $i$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| $C_i$ | 0 | $2\sqrt{3}$ | 0 | 0 | 0 | 0 | 0 | $2\sqrt{3}$ |
| $S_i$ | 0 | 2 | 0 | 0 | 0 | 0 | 0 | -2 |
このようになります.きちんと $\sin$ と $\cos$ に分解できていることが分かりました!
5.周波数から元の波形を復元
周波数に分解できたならば,元の波形を復元するのは簡単です.各周波数成分と波形のベクトルを掛けたものの総和を求めれば良いです.
入力信号ベクトルを $X_{in}$,$X_{in}$ と $C_i$ との内積を $f_{C_i}$, $S_i$ との内積を $f_{S_i}$ で表すとします.
例えば $f_{C_1}$ で,$X_{in}$ に 含まれる $C_1$ 周波数成分の量が分かります.
入力 $X_{in} = C_1$ のとき,$f_{C_1} = f_{C_7} = 4$,それ以外は0でした.
基底ベクトル $C_1$ のみを使って,$\frac{f_{C_1}}{\Vert C_1\Vert } = \frac{4}{4} = 1$ なので,$X_{in}$ に含まれる $C_1$ 成分は 1.基底ベクトルで内積が非 0 になるのはこれだけなので,もとの波形 $X_{out}$ は $1\times C_1 = C_1$
…と計算しても良いですが,
$$\bbox[#ded,20px]{X_{out} = \frac{1}{n}\sum_{i=0}^{n-1}C_if_{C_i} + S_if_{S_i}}$$
と計算します.$X_{in}=C_1$ のときは
$$X_{out} = \frac{1}{n}(C_1 \times f_{C_1} + C_7 \times f_{C_7}) = \frac{1}{8}(C_1 \times 4 + C_1 \times 4) = C_1$$
と$X_{in} = X_{out}$ となり,入力信号を復元することができました.
入力信号 $X_{in} = 2C_2-C_3+\frac{1}{4}S_3$ のとき,
$$
\begin{matrix}
f_{C_2} = f_{C_6} = 8\\
f_{C_3} = f_{C_5} = -4\\
f_{S_3} = 1\\
f_{S_5} = -1
\end{matrix}
$$
でした.よって
$$
X_{out} = \frac{1}{n}(C_2f_{C_2} + C_6f_{C_6} + C_3f_{C_3} + C_5f_{C_5} + S_3f_{S_3} + S_5f_{S_5})
$$
$$
= \frac{1}{8}(8C_2 + 8C_6 -4C_3 -4C_5 + 1S_3 -1(-S_3))
$$
$$
= 2C_2-C_3+\frac{1}{4}S_3
$$
と復元できました.
ここまでベクトル同士の演算で定義してきましたが,これらをまとめて 行列にします.
$$
\pmb{C} = \left(\begin{matrix}
C_0\\C_1\\C_2\\\vdots\\C_{n-1}
\end{matrix}\right),
\pmb{S} = \left(\begin{matrix}
S_0\\S_1\\S_2\\\vdots\\S_{n-1}
\end{matrix}\right)
$$
とします.行列の各要素 $\pmb{C_{a,b}}, \pmb{S_{a,b}}$ $(0 \leq a,b < n)$ は次のように表現できます.
$$\pmb{C}_{a,b} = \cos\left(\frac{360^o}{n}ab\right)$$
$$\pmb{S}_{a,b} = \sin\left(\frac{360^o}{n}ab\right)$$
$n = 8$ のときは
$$
\pmb{C} =
\left(\begin{matrix}
\color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1} & \color{#f00}{ 1}\\
\
\color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2}\\
\
\color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0}\\
\
\color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2}\\
\
\color{#f00}{ 1} & \color{#00f}{-1} & \color{#f00}{ 1} & \color{#00f}{-1} & \color{#f00}{ 1} & \color{#00f}{-1} & \color{#f00}{ 1} & \color{#00f}{-1}\\
\
\color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2}\\
\
\color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0}\\
\
\color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2}
\end{matrix}
\right)
$$
$$
\pmb{S} =
\left(\begin{matrix}
\color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} \\
\
\color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2}\\
\
\color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} \\
\
\color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2} & \color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2}\\
\
\color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} & \color{#000}{ 0} \\
\
\color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#f00}{ 1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#00f}{-1} & \color{#c00}{ \sqrt{2}/2}\\
\
\color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} & \color{#000}{ 0} & \color{#00f}{-1} & \color{#000}{ 0} & \color{#f00}{ 1} \\
\
\color{#000}{ 0} & \color{#00c}{-\sqrt{2}/2} & \color{#00f}{-1} & \color{#00c}{-\sqrt{2}/2} & \color{#000}{ 0} & \color{#c00}{ \sqrt{2}/2} & \color{#f00}{ 1} & \color{#c00}{ \sqrt{2}/2}\\
\
\end{matrix}
\right)
$$
WolframAlpha
です.
ここで,入力ベクトル $X_{in}$ から $\cos$ 成分ベクトル $F_C$, $\sin$ 成分ベクトル $F_S$, を抜き出すのは
$$
\bbox[#ded,20px]{
\begin{matrix}
F_C = \pmb{C}X_{in}\\
F_S = \pmb{S}X_{in}
\end{matrix}
}
$$
となり,$X_{out}$ を復元する操作は
$$
\bbox[#ded,20px]{X_{out} = \frac{\pmb{C}F_C + \pmb{S}F_S}{n}}
$$
で求めることができます.
$g[\theta] = 2\cos(2\theta) - \cos(3\theta) + \frac{1}{4}\sin(3\theta)$ を例に実際に計算する様子はこちら.
Fc ベクトルを求める(WolframAlpha)
Fs ベクトルを求める(WolframAlpha)
X を復元する(WolframAlpha)
g[θ]の値と同じであることを確認(WolframAlpha)
6.複素数を使って1つにまとめる
今まで,$\pmb{C}, \pmb{S}$ の2つの行列を使って表現してきました.行列2つを使うのは面倒くさいので,複素数 $i$ を用いて 1 つの複素行列 $\pmb{W}$ にまとめます.
$$
\pmb{W} = \pmb{C} + i\pmb{S}
$$
$$
\overline{\pmb{W}} = \pmb{C} - i\pmb{S}
$$
$\overline{\pmb{W}}$ は $\pmb{W}$ の虚部を正負反転したもので,複素共役 と言います.
$\pmb{W}$ にまとめても,$\pmb{W}$ の各ベクトル同士の内積は 0 になるので,直交基底になります.
Python による確認コードはこちら
import cmath
import numpy as np
N = 8
F = np.array([[cmath.rect(1, a*b * np.pi * 2 / N) for a in range(0, N)] for b in range(0, N)])
# Fの内容を表示
np.set_printoptions(precision=3, floatmode='fixed', suppress=True)
print(F)
# 各内積を表示
for a in range(N):
for b in range(N):
d = np.dot(F[a], F[b])
print("dot(F[{0}], F[{1}]) = {2:4.1f}{3:+4.1f}i".format(a, b, d.real, d.imag))
自分で実装して確かめたいというときは,複素ベクトル $A, B$ の内積は
$$
A \cdot B = \sum_{k=0}^{n-1} A_k\overline{B_k}
$$
となることに注意してください.
5章 で扱った周波数成分の分解・復元の式を,$\pmb{S} \leftarrow i\pmb{S}$ と代入し,さらに辻褄を合わせます.
$$
F_C = \pmb{C}X_{in}
$$
$$
iF_S = (i\pmb{S})X_{in}
$$
$$
X_{out} = \frac{\pmb{C}F_C + \frac{1}{i^2}(i\pmb{S})(iF_S)}{n} = \frac{\pmb{C}F_C - (i\pmb{S})(iF_S)}{n}
$$
ここで,$\pmb{S}$の対称性,$F_C$の対称性から $\pmb{S}F_C = 0$, 同様に $\pmb{C}F_S = 0$ であるので,
$$
X_{out} = \frac{\pmb{C}F_C - (i\pmb{S})(iF_S) -i\pmb{S}F_C +i\pmb{C}F_S}{n}
$$
$$
= \frac{(\pmb{C}-i\pmb{S})(F_{C}+iF_{S})}{n}
$$
周波数成分 $F_{C}, F_{S}$ も $F = F_{C} + iF_{S}$ とまとめて,以下のようになります.
$$
\bbox[#ded,20px]{
\begin{matrix}
F = \pmb{W}X_{in}\\X_{out} = \frac{1}{n}\overline{\pmb{W}}F
\end{matrix}
}
$$
この $F = \pmb{W}X_{in}$ という計算を 離散フーリエ変換, $X_{out} = \frac{1}{n}\overline{\pmb{W}}F$ を 逆離散フーリエ変換 と呼びます.
また,$X_{in} = X_{out}$ で あることから,
$$F = \frac{1}{n}\pmb{W}\overline{\pmb{W}}F $$
$$\pmb{W}^{-1} = \frac{1}{n}\overline{\pmb{W}}$$
であることも分かります.(WolframAlpha で確認)
$2\cos(2\theta) - \cos(3\theta) + \frac{1}{4}\sin(3\theta)$ の1周期分を $n=8$ でサンプリングした行列
$$G = (1, \frac{5}{4\sqrt{2}}, -\frac{9}{4}, -\frac{3}{4\sqrt{2}}, 3, -\frac{5}{4 \sqrt{2}}, -\frac{7}{4}, \frac{3}{4\sqrt{2}})^\top$$
を用いて実際に計算してみましょう.
行列を用いた場合,
$$F=\pmb{W}G = (0, 0, 8, -4+i, 0, -4-i, 8, 0)^\top$$
と離散フーリエ変換できます.(WolframAlphaで計算)
これは WolframAlphaの離散フーリエ変換関数の結果と一致します.(WolframAlphaはデフォルトで$1/\sqrt{n}$倍で計算するため,$\sqrt{n}$倍しています.)
次に行列を使い,逆変換します.
$$X_{out}=\frac{1}{n}\overline{\pmb{W}}F = (1, \frac{5}{4\sqrt{2}}, -\frac{9}{4}, -\frac{3}{4\sqrt{2}}, 3, -\frac{5}{4 \sqrt{2}}, -\frac{7}{4}, \frac{3}{4\sqrt{2}})^\top$$
となるので,無事に元のベクトル $G$ を復元できました.(WolframAlphaで計算)
これも WolframAlphaの逆離散フーリエ変換関数の結果と一致します.(WolframAlphaはデフォルトで$\sqrt{n}$倍で計算するため,$1/\sqrt{n}$倍しています.
今まで行列で表現してきましたが,$\sum$ を使って書き換えます.
$$\pmb{W}_{a,b} = \cos\left(\frac{360^o}{n}ab\right) + i\sin\left(\frac{360^o}{n}ab\right)$$
でしたので離散フーリエ変換と逆離散フーリエ変換はそれぞれ
$$
\bbox[#ded,20px]{
\begin{matrix}
F[a] = \sum\limits_{b=0}^{n-1}X[b]\left(\cos\left(\dfrac{360^o}{n}ab\right) + i\sin\left(\dfrac{360^o}{n}ab\right)\right)\\
X[a] = \dfrac{1}{n}\sum\limits_{b=0}^{n-1}F[b]\left(\cos\left(\dfrac{360^o}{n}ab\right) - i\sin\left(\dfrac{360^o}{n}ab\right)\right)
\end{matrix}
}
$$
と書けます.また,オイラーが導き出した,三角関数をネイピア数 $e$ の指数乗を使ってまとめるオイラーの公式
$$
e^{i\theta} = \cos\theta + i \sin\theta
$$
$$
e^{-i\theta} = \cos\theta - i \sin\theta
$$
と,$360^o$ という度数法を弧度法(ラジアン)を用いた $2\pi$ に書き換えて
$$
\bbox[#ded,20px]{
\begin{matrix}
F[a] = \sum\limits_{b=0}^{n-1}X[b]e^{i\left(\frac{2\pi}{n}ab\right)}\\
X[a] = \dfrac{1}{n}\sum\limits_{b=0}^{n-1}F[b]e^{-i\left(\frac{2\pi}{n}ab\right)}
\end{matrix}
}
$$
と書くのが,一般的です.
離散フーリエ変換には
- $1/n$ を正変換・逆変換どちらで行うか or 両方に平等に $1/\sqrt{n}$ を掛けるか.
- 指数関数の符号をどうするか
などの流儀により,いくつかの定義があります.具体的には
| 離散フーリエ変換(DFT) | 逆離散フーリエ変換(IDFT) | |
|---|---|---|
| (1) | $F[a] = \sum\limits_{b=0}^{n-1}X[b]e^{i\frac{2\pi}{n}ab}$ | $X[a] = \dfrac{1}{n}\sum\limits_{b=0}^{n-1}F[b]e^{-i\frac{2\pi}{n}ab}$ |
| (2) | $F[a] = \color{#f00}{\dfrac{1}{\sqrt{n}}}\sum\limits_{b=0}^{n-1}X[b]e^{i\frac{2\pi}{n}ab}$ | $X[a] = \color{#f00}{\dfrac{1}{\sqrt{n}}}\sum\limits_{b=0}^{n-1}F[b]e^{-i\frac{2\pi}{n}ab}$ |
| (3) | $F[a] = \sum\limits_{b=0}^{n-1}X[b]e^{\color{#f00}{-i}\frac{2\pi}{n}ab}$ | $X[a] = \dfrac{1}{n}\sum\limits_{b=0}^{n-1}F[b]e^{\color{#f00}{i}\frac{2\pi}{n}ab}$ |
などです.
(1) は今回導出したもので,Wolfram によるとデータ解析の文脈で主に使われるようです.
(2) はWolfram 言語デフォルトで採用されているものです.
(3) はWikipedia で書かれている定義であり,Wolfram によると信号処理の文脈で主に使われるようです.Intel MKL,Intel IPP,FFTW でもこちらの定義が使用されています(オプションにより変更可能).
Intel MKL/IPP, FFTW について
-
Intel MKL (Intel(R) Math Kernel Library)
Intel が開発している数値計算ライブラリです.Intel CPU 向けの最適化がメインにされています.複数ノードでの計算などにも対応した高度な数学計算向けのライブラリです.有料ですが学生なら Parallel Studio XE の付属ライブラリとしてインテルコンパイラなどとともに無料で使用できます.
Python の NumPy/SciPy では標準で OpenBLAS を使用しますが,MKL を持っていれば MKL を使うようにビルドすることもできます. -
Intel IPP(Intel(R) Integrated Performance Primitives)
同じく Intel が開発している,信号処理(1次元)・画像処理(2次元)向けの数値計算ライブラリです.これらの計算で使われる問題サイズ・次元数の場合は MKL より IPP の方が高速です.OpenCV は元々 Intel から提供されていた経緯によりIPPの一部機能が導入されており,IPP の高速な FFT 計算が使えます. -
FFTW
オープンソース・無料で使える高速フーリエ変換ライブラリの中では最速とされているライブラリです.
些細な違いはありますが,重要なのは
- DFT も IDFT も本質は同じである点
- 差は $1/n$ 倍をいつ行うかと指数関数の符号が異なる点
です.
7.補足
7.1 他に知っておくべき性質
今まで入力のベクトルは実数ベクトル $\mathbb{R}^n$ と仮定して,離散フーリエ変換により $\mathbb{R}^n \rightarrow \mathbb{C}^n$ (複素ベクトル) に移し,逆変換により $\mathbb{C}^n \rightarrow \mathbb{R}^n$ と戻してきました.
これは元々の入力が実数ベクトルの場合,正変換(・逆変換)後は共役対称性のある複素ベクトルになり,共役対称性のある複素ベクトルを逆変換(・正変換)した場合,実数ベクトルになるという性質のためです.
共役対称性とは長さ $n$ のベクトル$F$ に対し,
$$
\begin{matrix} F_0 = \overline{F_0} \\
F_i = \overline{F_{n-i}} & i = 1,...,n-1 \\
(\mathrm{imag}(F_0) = 0, & \mathrm{imag}(F_{n/2})=0)
\end{matrix}
$$
という対称性をもつ性質です.この特性を使うことにより,$n$ 要素の実数の入力に対し $2n$ 要素の実数の組である複素数を返すのではなく,$n$ (+パディング) 要素の実数だけで表現する Packed Format で出力することができるライブラリもあります.
ところで離散フーリエ変換は,一般化により入力として複素ベクトルも扱うことができます.その際,出力に共役対称性があるとは限らなくなるため,正変換も逆変換も $\mathbb{C}^n \rightarrow \mathbb{C}^n$ という変換になります.
これにより,証明に使った一部の変形が変わってしまいますが,
$$\pmb{W}^{-1} = \frac{1}{n}\overline{\pmb{W}}$$
は保たれるので正変換・逆変換ともにできます.
試しに,
$$
X = \left(\begin{matrix}
3 + 2i\\
1 + 7i\\
4 + 1i\\
1 + 8i\\
5 - 2i\\
9 + 8i\\
2 - 1i\\
6 - 8i\\
\end{matrix}\right)
$$
という複素ベクトルで試してみましょう.
$$
F = \pmb{W}X = \left(
\begin{array}{lcl}
31 & + & 15 i,\\
-4 - 9 \sqrt{2} & + & (6 - 15 \sqrt{2})i\\
-13 & + & 3 i\\
-6 \sqrt{2} & + & (2 + 2 \sqrt{2})i\\
-3 & - & 15 i\\
-4 + 9 \sqrt{2} & + & (6 + 15 \sqrt{2})i\\
17 & - & 3 i\\
6 \sqrt{2} & + & (2 - 2 \sqrt{2})i\\
\end{array}
\right)
$$
と離散フーリエ変換でき,
(WolframAlphaで行列積を計算,WolframAlphaの離散フーリエ変換関数の結果)
$$
X = \frac{1}{n}\overline{\pmb{W}}F = \left(\begin{matrix}
3 + 2i\\
1 + 7i\\
4 + 1i\\
1 + 8i\\
5 - 2i\\
9 + 8i\\
2 - 1i\\
6 - 8i\\
\end{matrix}\right)
$$
(WolframAlphaで行列積を計算,WolframAlphaの逆離散フーリエ変換関数の結果)
と逆変換もできました.
また,今まで例として $n = 8$ を用いていましたが,これ以外の正整数でも対応できます.
$n = 4$ のときは
$$
\pmb{W} = \left(\begin{matrix}
\underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1}\\
\underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#7f0}{\Rule{3ex}{0.4ex}{0px}}}{ i} & \underset{\color{#0ff}{\Rule{3ex}{0.4ex}{0px}}}{-1} & \underset{\color{#70f}{\Rule{3ex}{0.4ex}{0px}}}{-i}\\
\underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#0ff}{\Rule{3ex}{0.4ex}{0px}}}{-1} & \underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#0ff}{\Rule{3ex}{0.4ex}{0px}}}{-1}\\
\underset{\color{#f00}{\Rule{3ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#70f}{\Rule{3ex}{0.4ex}{0px}}}{-i} & \underset{\color{#0ff}{\Rule{3ex}{0.4ex}{0px}}}{-1} & \underset{\color{#7f0}{\Rule{3ex}{0.4ex}{0px}}}{ i}\\
\end{matrix}\right)
$$
となります.この程度なら手計算で離散フーリエ変換も出来そうですね.
$n = 6$ のときは
$$
\pmb{W} = \left(\begin{matrix}
\underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1}\\
\underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#dd2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{ 1+\sqrt{3}i}{2} } & \underset{\color{#2d2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1+\sqrt{3}i}{2} } & \underset{\color{#2dd}{\Rule{6ex}{0.4ex}{0px}}}{-1 } & \underset{\color{#22d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1-\sqrt{3}i}{2} } & \underset{\color{#d2d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{ 1-\sqrt{3}i}{2} }\\
\underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#2d2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1+\sqrt{3}i}{2} } & \underset{\color{#22d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1-\sqrt{3}i}{2} } & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#2d2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1+\sqrt{3}i}{2} } & \underset{\color{#22d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1-\sqrt{3}i}{2} }\\
\underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#2dd}{\Rule{6ex}{0.4ex}{0px}}}{-1 } & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#2dd}{\Rule{6ex}{0.4ex}{0px}}}{-1 } & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#2dd}{\Rule{6ex}{0.4ex}{0px}}}{-1 }\\
\underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#22d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1-\sqrt{3}i}{2} } & \underset{\color{#2d2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1+\sqrt{3}i}{2} } & \underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#22d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1-\sqrt{3}i}{2} } & \underset{\color{#2d2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1+\sqrt{3}i}{2} }\\
\underset{\color{#d22}{\Rule{6ex}{0.4ex}{0px}}}{ 1} & \underset{\color{#d2d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{ 1-\sqrt{3}i}{2} } & \underset{\color{#22d}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1-\sqrt{3}i}{2} } & \underset{\color{#2dd}{\Rule{6ex}{0.4ex}{0px}}}{-1 } & \underset{\color{#2d2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{-1+\sqrt{3}i}{2} } & \underset{\color{#dd2}{\Rule{6ex}{0.4ex}{0px}}}{\frac{ 1+\sqrt{3}i}{2} }\\
\end{matrix}\right)
$$
の様になります.
各値の識別のために色付き下線を付けました.以下,登場する値を色と一緒にプロットしたものです.
また,
$$\pmb{W}_{a,b} = e^{i\frac{360^o}{n}ab} = \cos\left(\frac{360^o}{n}ab\right) + i\sin\left(\frac{360^o}{n}ab\right)$$
でしたが,
$$
w = e^{i\frac{360^o}{n}} = \cos\left(\frac{360^o}{n}\right) + i\sin\left(\frac{360^o}{n}\right)
$$
と置いて,指数法則 $a^{xn} = (a^x)^n$ または ド・モアブルの定理
$$
\cos(n\theta) + i \sin(n\theta) = (\cos\theta + i\sin\theta)^n
$$
を用いて
$$
\pmb{W} = \left(\begin{matrix}
w^{0} & w^{0} & w^{0} & w^{0} & w^{0} & w^{0}\\
w^{0} & w^{1} & w^{2} & w^{3} & w^{4} & w^{5}\\
w^{0} & w^{2} & w^{4} & w^{6} & w^{8} & w^{10}\\
w^{0} & w^{3} & w^{6} & w^{9} & w^{12} & w^{15}\\
w^{0} & w^{4} & w^{8} & w^{12} & w^{16} & w^{20}\\
w^{0} & w^{5} & w^{10} & w^{15} & w^{20} & w^{25}\\
\end{matrix}\right)
$$
更に $w^n = \cos(360^oab) + i\sin(360^oab) = 1$ である事実を用いて,
$$
\pmb{W} = \left(\begin{matrix}
w^{0} & w^{0} & w^{0} & w^{0} & w^{0} & w^{0}\\
w^{0} & w^{1} & w^{2} & w^{3} & w^{4} & w^{5}\\
w^{0} & w^{2} & w^{4} & w^{0} & w^{2} & w^{4}\\
w^{0} & w^{3} & w^{0} & w^{3} & w^{0} & w^{3}\\
w^{0} & w^{4} & w^{2} & w^{0} & w^{4} & w^{2}\\
w^{0} & w^{5} & w^{4} & w^{3} & w^{2} & w^{1}\\
\end{matrix}\right)
$$
と置き換えることもできます.($n = 6$ の場合の例)
この事実を使うことで,($n$ を素因数分解したとき小さな素数のみで構成される場合,)DFT の計算量を $O(n^2)$ から $O(n\log n)$ にまで落とす FFT と言う技法があります.
7.2 離散コサイン変換(DCT)
離散コサイン変換とは,離散フーリエ変換をアレンジした変換です.
Jpeg や Mpeg などの画像・動画圧縮に使われているアルゴリズムです.
わき道だけど長めなので折りたたみます
離散フーリエ変換によって全ての周期的な離散信号は,偶関数である $\cos$ と 奇関数である $\sin$ に分解できることが分かりました.
ところで実数値を取る偶関数な周期信号を離散フーリエ変換するとどうなるでしょう? 偶関数は偶関数の波の重ね合わせで表現できるので,偶関数つまり $\cos$ 成分のみに分解することができます.複素ベクトルでいうとこの複素ベクトルには実数成分しか存在しません.
逆に奇関数な周期信号を離散フーリエ変換すると,奇関数である $\sin$ のみで表現可能になり,出力の複素ベクトルには虚数成分しか現れません.
例えば以下のような長さ $n = 8$ で偶対称性のある実数ベクトルを考えます.
$$
X = \left(\begin{matrix}
1 & 2 & 3 & 4 & 6 & 4 & 3 & 2
\end{matrix}\right)^\top
$$
$X_1 = X_7 = 2$ のように $X_i = X_{-i \bmod n} = X_{n-i}$ という対称性が成り立つので,これは偶対称です.
これを離散フーリエ変換したものは,実数ベクトルになります.
$$
\pmb{W}X = \left(\begin{matrix}
25 \\
-5-2\sqrt{2}\\
1\\
-5 + 2\sqrt{2}\\
1\\
-5 + 2\sqrt{2}\\
1\\
-5 - 2\sqrt{2}
\end{matrix}\right)
$$
WolframAlphaで確認(行列ver.)
WolframAlphaで確認(組み込み関数ver.)
また,以下のような長さ $n = 8$ で奇対称性のある実数ベクトルを考えます.
$$
Y = \left(\begin{matrix}
0 & 1 & 2 & 3 & 0 & -3 & -2 & -1
\end{matrix}\right)^\top
$$
$Y_1 = -Y_7 = 1$ のように $Y_i = -Y_{-i \bmod n} = -Y_{n-i}$ という対称性が成り立つので,これは奇対称です.
これを離散フーリエ変換したものは,純虚数ベクトルになります.
$$
\pmb{W}Y = \left(\begin{matrix}
0i\\
(4 + 4\sqrt{2})i\\
-4 i\\
(-4+4\sqrt{2})i\\
0i\\
(4 - 4\sqrt{2})i\\
4 i\\
(-4 - 4\sqrt{2})i
\end{matrix}\right)
$$
WolframAlphaで確認(行列ver.)
WolframAlphaで確認(組み込み関数ver.)
つまり,入力値に偶対称性(・奇対称性)があれば,$\mathbb{R}^n \rightarrow \mathbb{R}^n$ という変換ができるようになります.
離散コサイン変換(や離散サイン変換 )は,入力ベクトル自体に対称性があると仮定する事によって,$\mathbb{R}^n \rightarrow \mathbb{R}^n$ という嬉しい性質が発生する事を利用した変換です.
離散コサイン変換(DCT)にはその入力の対称性の仮定の仕方により,DCT-I から DCT-VIII まで定義されています.
今回はその中でもメジャーな DCT-I と.DCT-II / III について解説します.
7.2.1 DCT-I
DCT-Iでは,$1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, ...$ のような対称性を仮定したDCTです.
この場合,DCT の入力としては先頭の $1, 2, 3, 4, 5$ の 5 要素があれば十分ですね.この要素数を $n$ と置きます.
またこの入力を離散フーリエ変換の入力,つまり周期信号として見たときは $1, 2, 3, 4, 5, 4, 3, 2$ の 8 要素でループしています.この要素数を $n' = 2n-2$ とします.
入力 $X_{in}$ を離散コサイン変換した結果を $F$,$F$ を逆離散コサイン変換した結果を $X_{out}$ とすると,行列表現を用いて以下のように計算できます.
$$
\bbox[#ded,20px]{
\begin{matrix}
F = \pmb{C}X_{in}\\
X_{out} = \dfrac{1}{n'}\pmb{C}F\\
\pmb{C}_{a,b} = \begin{cases}
\cos\left(\dfrac{360^o}{n}ab\right) & (b = 0 \ or\ n-1)\\
2\cos\left(\dfrac{360^o}{n}ab\right) & (otherwise)
\end{cases}
\end{matrix}
}
$$
$n = 5$ を例に行列 $\pmb{C}$ を示すと以下の通りになります.
$$
\pmb{C} = \left(\begin{matrix}
\cos{0^o} & 2\cos{ 0^o} & 2\cos{ 0^o} & 2\cos{ 0^o} & \cos{ 0^o}\\
\cos{0^o} & 2\cos{ 45^o} & 2\cos{ 90^o} & 2\cos{135^o} & \cos{180^o}\\
\cos{0^o} & 2\cos{ 90^o} & 2\cos{180^o} & 2\cos{270^o} & \cos{360^o}\\
\cos{0^o} & 2\cos{135^o} & 2\cos{270^o} & 2\cos{405^o} & \cos{540^o}\\
\cos{0^o} & 2\cos{180^o} & 2\cos{360^o} & 2\cos{540^o} & \cos{720^o}\\
\end{matrix}\right)
$$
$$
=\left(\begin{matrix}
1 & 2 & 2 & 2 & 1\\
1 & \sqrt{2} & 0 & -\sqrt{2} & -1\\
1 & 0 & -2 & 0 & 1\\
1 & -\sqrt{2} & 0 & \sqrt{2} & -1\\
1 & -2 & 2 & -2 & 1\\
\end{matrix}\right)
$$
離散フーリエ変換の $\cos$ パートと似たような要素になります.対称性による折り返しの分,端以外は2倍になっています.
逆変換に関して,$\pmb{C}$ の逆行列 $\pmb{C}^{-1} = \frac{1}{n'}\pmb{C}$ という関係があります.
実際に $X_{in} = \left(\begin{matrix}1 & 2 & 3 & 4 & 6\end{matrix}\right)^\top$ というデータを例に計算してみましょう.
$$
F=\pmb{C}X_{in} = \left(\begin{matrix}
25 \\
-5-2\sqrt{2}\\
1\\
-5 + 2\sqrt{2}\\
1
\end{matrix}\right)
$$
$\left(\begin{matrix}1 & 2 & 3 & 4 & 6 & 4 & 3 & 2\end{matrix}\right)^\top$ を離散フーリエ変換した結果の前半 5 個分と同じ結果になりました.
逆変換も
$$
X_{out} =\frac{1}{8}\pmb{C}F = \left(\begin{matrix}1 & 2 & 3 & 4 & 6\end{matrix}\right)^\top
$$
と,元の入力と一致しました.
WolframAlphaで確認
7.2.2 DCT-II / III
DCT-I では入力の境界の要素を繰り返しませんでした.これによって離散フーリエ変換と互換性のある結果を得ることができました.
DCT-II / III では,$1,2,3,4,\ 4,3,2,1,\ 1,2,3,4,\ ...$ といった,端の要素も繰り返すような周期性を仮定します.
これは離散フーリエ変換やDCT-Iと比較してサンプルするところを半分ずらす操作になります.
グラフでイメージすると以下のようになります.
DCT-II と DCT-III は正変換と逆変換の関係にあり,以下のように求められます.
$$
\bbox[#ded,20px]{
\begin{matrix}
F = \pmb{C}X_{in}\\
X_{out} = \pmb{C}^{-1}F\\
\pmb{C_{a,b}} = 2\cos\left(\dfrac{360^o}{4n}a(2b+1)\right)\\
\pmb{C_{a,b}}^{-1} = \begin{cases}
\dfrac{1}{2n}\times\cos(0) = \dfrac{1}{2n} & (b = 0)\\
\dfrac{1}{2n}\times2\cos\left(\dfrac{360^o}{4n}(2a+1)b\right) & (otherwise)
\end{cases}
\end{matrix}
}
$$
$n = 4$ を例に行列 $\pmb{C}, \pmb{C}^{-1}$ を示すと以下の通りになります.
$$
\pmb{C} = 2\left(\begin{matrix}
\cos{ 0^o} & \cos{ 0^o} & \cos{ 0^o} & \cos{ 0^o}\\
\cos{ 22.5^o} & \cos{ 67.5^o} & \cos{112.5^o} & \cos{157.5^o}\\
\cos{ 45.0^o} & \cos{135.0^o} & \cos{225.0^o} & \cos{315.0^o}\\
\cos{ 67.5^o} & \cos{202.5^o} & \cos{337.5^o} & \cos{472.5^o}
\end{matrix}\right)
$$
$$
=\left(\begin{matrix}
2 & 2 & 2 & 2 \\
\sqrt{2+\sqrt{2}} & \sqrt{2-\sqrt{2}} & -\sqrt{2-\sqrt{2}} & -\sqrt{2+\sqrt{2}} \\
\sqrt{2} & -\sqrt{2} & -\sqrt{2} & \sqrt{2} \\
\sqrt{2-\sqrt{2}} & -\sqrt{2+\sqrt{2}}& \sqrt{2+\sqrt{2}} & -\sqrt{2-\sqrt{2}} \\
\end{matrix}\right)
$$
$$
\pmb{C}^{-1} = \frac{1}{8}\left(\begin{matrix}
1 & \sqrt{2+\sqrt2} & \sqrt2 & \sqrt{2-\sqrt2}\\
1 & \sqrt{2-\sqrt2} & -\sqrt2 & -\sqrt{2+\sqrt2}\\
1 & -\sqrt{2-\sqrt2} & -\sqrt2 & \sqrt{2+\sqrt2}\\
1 & -\sqrt{2+\sqrt2} & \sqrt2 & -\sqrt{2-\sqrt2}\\
\end{matrix}\right)
$$
$\pmb{C}$ と $\pmb{C}^{-1}$ は定数倍を除いて,ほぼ転置の関係になります.
離散フーリエ変換やDCT-Iと比較してサンプル箇所が変わるので形や結果が変わりますが,これでも計算することができます.
実際に $X_{in} = \left(\begin{matrix} 3 & 1 & 4 & 5\end{matrix}\right)^\top$ というデータを例に計算してみましょう.
$$
F=\pmb{C}X_{in} = \left(\begin{matrix}
26\\
-3 \sqrt{2 - \sqrt2} - 2 \sqrt{2 + \sqrt2}\\
3 \sqrt2\\
-2 \sqrt{2 - \sqrt2} + 3 \sqrt{2 + \sqrt2}
\end{matrix}\right) \simeq \left(\begin{matrix}
26\\
-5.99162\\
4.24264\\
4.01254\\
\end{matrix}\right)
$$
WolframAlphaで確認(行列ver.)
WolframAlphaで確認(組み込み関数ver.)
WolframAlpha の FourierDCT はデフォルトで DCT-II なのですが,定数倍を除いて一致しました.
逆変換も
$$
X_{out} =\pmb{C}^{-1}F = \left(\begin{matrix}3 & 1 & 4 & 5\end{matrix}\right)^\top
$$
と,元の入力と一致しました.
WolframAlphaで確認
7.2.3 離散コサイン変換のメリット
離散フーリエ変換では $\mathbb{R}^n \rightarrow \mathbb{C}^n$ という変換になってしまうのが,DCTでは$\mathbb{R}^n \rightarrow \mathbb{R}^n$ という点で1つ有利と紹介しました.
また,適当なデータを離散フーリエ変換するとき,1周期分をまたぐ場所で値が大きく飛んでしまうことが多々あります(非連続である).これに対して離散コサイン変換では折返しの周期性を仮定するので,1周期分をまたぐ場所でも連続的になります.
非連続なグラフの方が連続なグラフよりもたくさんの $\cos/\sin$カーブで細かく補完しないといけなさそうなのは直感でもピンと来るでしょう.つまり離散コサイン変換は離散フーリエ変換に比べ,結果データは秩序的になることが期待されます.
JPEG などの画像符号化では 8x8 ブロックなどの小さな単位に分けて離散コサイン変換を行い,変換結果を圧縮してデータ量を減らすのですが,秩序的なデータの方が圧縮効率が良くなるので離散コサインが使用されます.
7.3 非周期関数を離散フーリエ変換するとどうなるの?
わき道だけど図などが長めなので折りたたみます
離散フーリエ変換では周期関数に含まれる周波数成分を分解・復元することができました.
ところで,非周期関数を突っ込んだらどうなるか,気になりませんか? 例えば $\cos\left(\frac{4}{3}\theta\right)$ のように,$360^o$ 周期ではない関数とか…?
と言っても,離散フーリエ変換は入力を周期関数と仮定して処理するので,入力がどんな形をしていようが関係ありません.$\cos\left(\frac{4}{3}\theta\right)$ を $360^o$ 周期としてサンプリングすると,下のような波形の周期関数として処理します.
これを $n = 8$ でサンプリングし,離散フーリエ変換すると以下の様になります.
この周波数成分を元に元の波形を復元すると,次のようなグラフになります.
…たしかにサンプリングした点は通過していますが,途中の補間された箇所はいびつですね…
左下の棒グラフは各周波数成分の量で,青が $\cos$ 成分,赤が $\sin$ 成分です.
右下の棒グラフは,パワースペクトル $\sqrt{C_i^2 + S_i^2}$ を示し,色は $\mathrm{arctan2}(S_i, C_i)$ によって位相角度を求め,位相に応じた色相でグラデーションしています.
$\cos\left(\frac{4}{3}\theta\right)$ なので,本当は $\frac{4}{3}$ のところのみスペクトルが反応してほしいのですが,棒グラフは離散的で $\frac{4}{3}$ を示すところが無いので周りに広がってしまっています.
サンプル数を増やしたらどうなるでしょうか? $n = 64$ でサンプリングしてみました.
状況はあまり変わりませんね….
$360^o$ 毎に非連続なのも悪さをしているのかもしれません.$\sin(1.5\theta)$ で試してみます.
$\sin$ 関数を元にしたはずですが,グラフが偶関数になったので $\cos$ 成分しか抽出されないのは面白いですね.
やはりサンプリングした範囲できちんと周期的でないと,元の周波数成分を完全に分解することはできません.
サンプリング数 $n$ をいくら増やしたとしても高周波な波を抽出できるようになるだけであり,周波数の分解能は増えません.今回の場合,周波数の分解能は 1 なので,1 Hz単位の波しか抽出できないのです.
たとえば音源の周波数を解析しようとした場合,サンプルが 1 秒の場合は 1Hz 単位,0.25 秒のサンプルの場合は 4 Hz 単位の分解能でしか解析できません.これはサンプリング周波数 192 kHz のようなハイレゾ音源でも変わりません.
音源解析では短い時間で変化する音の周波数を解析したいことがありますが,サンプルが0.25 秒の様に短いと低音域が潰れてしまいます.例えば 88鍵あるグランドピアノの中央のラ(A4)は 440 Hz,その右の黒鍵ラ# は 466.164 Hz です.中央付近は半音で26 Hz の差がありますが,一番低い左端のラ(A0) は27.5 Hz,ラ#は 29.135 Hz,シは30.868 Hz です.4Hz の分解能ではこれらの音の区別をすることはできません.
これはフーリエ変換の不確定性原理によるものです.絶対音感を持った人ならば 0.25 秒(のループ音源)しか聞けなくてもこれらの音を区別できる気はするのですが,単純な DFT では解析できないのは悔しいですね.
実際の音源解析では,サンプルの両端を0に近づけて滑らかにしてから周波数の解析を行います.この滑らかにする関数を窓関数と呼び,三角窓,ハミング窓,ブラックマン窓など,様々な種類があります.これにより偽の高周波を抑える効果は上がりますが,周波数の分解能は良くなりません(むしろ曖昧にあることもある).
この DFT による音階解析の限界に対応すべく,DFT を応用した Constant-Q 変換(定Q変換) などがあります.良かったら調べてみてください.
Python3 によるソースコード
import matplotlib.pyplot as plt
import numpy as np
import colorsys
N = 64
x = np.arange(-360, 360*2, min(1, 90/N))
xd = np.arange(-360, 360*2, 360/N)
xs = np.arange(0, 360, 360/N)
yd = np.cos(xs*8/6*np.pi/180)
#yd = np.sin(xs*1.5*np.pi/180)
dc = np.zeros(N)
ds = np.zeros(N)
yr = x * 0.0
yrd = xd * 0.0
for i in range(N):
dc[i] = np.dot(yd, np.cos(xs*(i * np.pi/180)))
ds[i] = np.dot(yd, np.sin(xs*(i * np.pi/180)))
yr += dc[i] * np.cos(x *(i * np.pi/180))
yr += ds[i] * np.sin(x *(i * np.pi/180))
yrd += dc[i] * np.cos(xd*(i * np.pi/180))
yrd += ds[i] * np.sin(xd*(i * np.pi/180))
yr /= N
yrd /= N
fig = plt.figure(figsize=(9, 5))
sub = fig.add_subplot(2, 1, 1)
sub.set_title(r"$\cos[\frac{4}{3}\theta] ...?$")
sub.set_xticks(np.linspace(-360, 360*2, 12+1))
sub.set_xticks(np.linspace(-360, 360*2, 24+1), minor=True)
sub.set_xticklabels([str(v)+"$^o$" for v in range(-360, 360*2+1, 90)])
sub.set_yticks(np.linspace(-1, 1, 4+1))
sub.set_xlim(-90, 360+90)
sub.set_ylim(min(-1., np.min(yr)), max(1., np.max(yr)))
sub.grid(which='both')
sub.plot(x, yr, label="cos")
sub.plot(xd, yrd, color="b", marker="o", linestyle='None')
sub.axvspan(0, 360, color="cyan", alpha=0.2)
W = 0.4
sub = fig.add_subplot(2, 2, 3)
sub.bar(np.arange(0, N/2+1, 1)-W/2, dc[0:N//2+1], alpha=1, color="blue", width=W)
sub.bar(np.arange(0, N/2+1, 1)+W/2, ds[0:N//2+1], alpha=1, color="orangered", width=W)
sub.grid(axis='x', b=True, which='major', color='0.75')
sub.grid(axis='y', b=True, which='major', color='0.75')
sub.set_xticks(np.linspace(0, N//2, 8+1))
sub = fig.add_subplot(2, 2, 4)
a = np.arctan2(ds, dc)
col = np.array([(colorsys.hsv_to_rgb(v/(2*np.pi)%1, 0.95, 0.95)) for v in a])
W = 0.9
sub.bar(np.arange(0, N/2+1, 1), np.sqrt(dc*dc+ds*ds)[0:N//2+1], color=col, width=W)
sub.grid(axis='y', b=True, which='major', color='0.75')
sub.set_xticks(np.linspace(0, N//2, min(N//2, 8)+1))
plt.show()
7.4 有名な波を離散フーリエ変換してみた
わき道だけど図などが長めなので折りたたみます
ここでは,離散フーリエ変換のときによく話題になる周期波を離散フーリエ変換してみた結果をまとめます.
$360^o$ で1周する波として,$n = 128$ でサンプリング.グラフは $-180^o ~ 180^o$ の部分のみを表示し,左右でつながって周期的な信号ベクトルであるとします.
また今回扱う波は全て偶関数,つまり $0^o$ の軸で左右対称な波を扱います.偶関数なので周波数成分は全て $\cos$ の周波数のみ表示します.
まずは常に 1.0 になる定数波(?)です.
$cos(0)$ のみの定数成分に分解できるので,0 の部分のみ値があり,他は全て0です.$n = 128$ なので,0の成分は 128 です.
次に $0^o$ のみ 1,ほかは 0 の インパルスです.
インパルスを離散フーリエ変換すると,全ての $\cos$ 成分が 1 になりました.全ての倍音の周波数成分を等しく混ぜるとインパルスになると言うことですね.
ところで,定数波とインパルスは離散フーリエ変換によって互いに相手の関数の形になったことに気づくと思います.
これは離散フーリエ変換の特徴の 1 つで,離散フーリエ変換と逆離散フーリエ変換の公式がほぼ同じことからも理由はすぐに分かると思います.
次は $|\theta| < 11.25^o$ のときは 1,他は 0 の 矩形波です.
次に $|\theta| < 22.5^o$ のときは 1,他は 0 の 矩形波です.
元の波を広げると周波数のグラフは狭く,元の波を狭めると周波数のグラフは広がります.
矩形波を離散フーリエ変換すると,$\mathrm{sinc}$ 関数の形になります.sinc 関数とは
$$
\mathrm{sinc}(x)=\begin{cases}
\dfrac{\sin(x)}{x}\ (x\neq 0) \\
1\ \ \ \ \ \ \ \ \ \ (x=0)
\end{cases}
$$
で表せられる関数で,信号処理などの工学分野でよく使う有名な関数です.
$\mathrm{sinc}$ を離散フーリエ変換すると,やはり矩形になります.
$\mathrm{sinc}$ 波の端が 0 に収束しきっていないので矩形波の端にノイズが乗ってしまいましたが,矩形波と$\mathrm{sinc}$ 波は離散フーリエ変換すると,互いに相手の形になることが分かったと思います.
最後に正規分布などでもおなじみ,ガウス関数
$$
f(x) = a e^{-(x/c)^2}
$$
です.
ガウス関数は離散フーリエ変換してもガウス関数の形になることが知られています.
Python3 によるソースコード
import matplotlib.pyplot as plt
import numpy as np
N = 128
x = np.arange(-360, 360*2, min(1, 90/N))
xd = np.arange(-360, 360*2, 360/N)
xs = np.arange(0, 360, 360/N)
xsa = (xs+180)%360-180
name = "Square2"
#yd = np.array([1.0 for v in xsa]) # 定数 Const
#yd = np.array([1.0 if v == 0 else 0 for v in xsa]) # パルス Pulse
#yd = np.array([1.0 if abs(v) < 180/16 else 0 for v in xsa]) # 矩形 Square
yd = np.array([1.0 if abs(v) < 180/8 else 0 for v in xsa]) # 矩形 Square2
#yd = np.array([1.0 if v == 0 else np.sin(v/6)/(v/6) for v in xsa]) # 矩形 Sinc
#yd = np.exp(-np.power(xsa/12,2)) # Gauss
dc = np.zeros(N)
ds = np.zeros(N)
yr = x * 0.0
yrd = xd * 0.0
for i in range(N):
dc[i] = np.dot(yd, np.cos(xs*(i * np.pi/180)))
ds[i] = np.dot(yd, np.sin(xs*(i * np.pi/180)))
yr += dc[i] * np.cos(x *(i * np.pi/180))
yr += ds[i] * np.sin(x *(i * np.pi/180))
yrd += dc[i] * np.cos(xd*(i * np.pi/180))
yrd += ds[i] * np.sin(xd*(i * np.pi/180))
yr /= N
yrd /= N
fig = plt.figure(figsize=(9, 5))
sub = fig.add_subplot(2, 1, 1)
sub.set_title(name)
sub.set_xticks(np.linspace(-360, 360*2, 24+1))
sub.set_xticks(np.linspace(-360, 360*2, 72+1), minor=True)
sub.set_xticklabels([str(v)+"$^o$" for v in range(-360, 360*2+1, 45)])
sub.set_yticks(np.linspace(-1, 1, 4+1))
sub.set_xlim(-180, 180)
sub.set_ylim(min(-1., np.min(yr)), max(1., np.max(yr)))
sub.grid(which='both')
sub.plot(x, yr, label="cos")
sub.plot(xd, yrd, color="b", marker="o", linestyle='None')
sub.axvspan(0, 360, color="cyan", alpha=0.2)
W = 0.45
sub = fig.add_subplot(2, 1, 2)
sub.bar(np.arange(0, N/2+1, 1)-W/2, dc[0:N//2+1], alpha=1, color="gold", width=W)
sub.bar(np.arange(0, N/2+1, 1)+W/2, ds[0:N//2+1], alpha=1, color="orangered", width=W)
sub.grid(axis='x', b=True, which='major', color='0.75')
sub.grid(axis='y', b=True, which='major', color='0.75')
sub.set_xticks(np.linspace(0, N//2, 16+1))
plt.show()
8.最後に
できるだけ易しく,離散フーリエ変換の解説・導出をしてみましたが,どうでしょうか?
ここまでの説明を読んで理解できれば,FFTについての解説もすんなりと分かるようになっていると思います(?)
この記事を読んで Good と感じたらぜひ「いいね」やTweetをお願いいたします.
それでは!
参考
やる夫で学ぶディジタル信号処理
慶應大学講義 物理情報数学C
FFT についての解説
東京工業大学デジタル創作同好会traP すく(0214sh7) さんによる解説
競プロのための高速フーリエ変換(ふるやんさんによる解説)
kaage さんによる解説
AtCoder による解説
るまライブラリによる解説
ngtkana さんによる解説