涌井良幸「高校生からわかるフーリエ解析(2019年)」第1章の内容がコンピューター言語による検証向けだったので、統計言語Rによるプログラミングにチャレンジしてみました。
高校生からわかるフーリエ解析 Kindle版
フーリエ級数展開(Fourier Series Expansion)の世界
そもそも「フーリエ解析(Fourier Analysis)」は、全ての波形について(Sin波やCos波の様な)正弦波に適正な数字を掛けて足し合わせたら再現可能と考えます。
①正弦波を特徴付ける主要パラメーター(Parameter、媒介変数、補助変数、母数、引数、設定値などの意味を持つ英単語。 IT分野ではそのソフトウェアやシステムの挙動に影響を与える、外部から投入されるデータなどのことを指す)は「振幅(Amplitude、基本円ではx<=|1|)」と「**波長**(wavelength、基本円では2π)」/「**位相**(Phase、単位はラジアン/秒)」/「**周波数**(frequency、基本円では位相/波長)」などである。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。

# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル定義
Main_title<-c("Amplitude & Frequency")
x_title<-c("X")
y_title<-c("Y")
# グラフのスケール決定
gs_x<-c(-pi,pi)
gs_y<-c(-3,3)
# y=sin(x)
f1_name<-c("y=sin(x)")
glaph_y1<-function(x) {sin(x)}
# y=2*sin(x)
f2_name<-c("y=2*sin(x)")
glaph_y2<-function(x) {2*sin(x)}
# y=3*sin(x)
f3_name<-c("y=3*sin(x)")
glaph_y3<-function(x) {3*sin(x)}
# y=sin(x*2)
f4_name<-c("sin(x*2)")
glaph_y4<-function(x) {sin(x*2)}
# y=sin(x*3)
f5_name<-c("y=sin(x*3)")
glaph_y5<-function(x) {sin(x*3)}
# y=sin(x*4)
f6_name<-c("y=sin(x*4)")
glaph_y6<-function(x) {sin(x*4)}
# グラフ描画
plot(glaph_y1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(glaph_y2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y4,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y5,xlim=gs_x,ylim=gs_y,type="l",col=Cyan, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y6,xlim=gs_x,ylim=gs_y,type="l",col=Yellow, main="",xlab="",ylab="")
# par(new=T)#上書き指定
# plot(f7,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
# 基準線
abline(h=0)
abline(v=0)
# 凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name,f4_name,f5_name,f6_name),lty=c(1,1,1,1,1,1),col=c(Red,Magenta,Blue,Green,Cyan,Yellow))
②定数倍した正弦波を幾つか足し合わせただけでも、それなりに複雑な波形が合成可能である。
実例1「y=-sin(x)+cos(x2)+1/2sin(x*3)」

# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル定義
Main_title<-c("Mix of Sine waves ")
x_title<-c("X")
y_title<-c("Y")
# グラフのスケール決定
gs_x<-c(-pi,pi)
gs_y<-c(-3,3)
# y=sin(x)
f1_name<-c("sin(x)")
glaph_y1<-function(x) {sin(x)}
# y=sin(x*2)
f2_name<-c("sin(x*2)")
glaph_y2<-function(x) {sin(x*2)}
# y=sin(x*3)
f3_name<-c("sin(x*3)")
glaph_y3<-function(x) {sin(x*3)}
# y=sin(x)+sin(x*2)+sin(x*3)
f4_name<-c("mix of these")
glaph_y4<-function(x) {sin(x)+sin(x*2)+sin(x*3)}
# グラフ描画
plot(glaph_y1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(glaph_y2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y4,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
# 基準線
abline(h=0)
abline(v=0)
# 凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name,f4_name),lty=c(1,1,1,1),col=c(Red,Magenta,Blue,Black))
実例2「y=-sin(x)+cos(x2)+1/2sin(x*3)」

# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル定義
Main_title<-c("Mix of Sine waves")
x_title<-c("X")
y_title<-c("Y")
# グラフのスケール決定
gs_x<-c(-pi,pi)
gs_y<-c(-3,3)
# y=-sin(x)
f1_name<-c("-sin(x)")
glaph_y1<-function(x) {-sin(x)}
# y=cos(x*2)
f2_name<-c("cos(x*2)")
glaph_y2<-function(x) {cos(x*2)}
# y=1/2*sin(x*3)
f3_name<-c("1/2*sin(x*3)")
glaph_y3<-function(x) {1/2*sin(x*3)}
# y=-sin(x)+cos(x*2)+1/2*sin(x*3)
f4_name<-c("mix of these")
glaph_y4<-function(x) {-sin(x)+cos(x*2)+1/2*sin(x*3)}
# グラフ描画
plot(glaph_y1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(glaph_y2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y4,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
# 基準線
abline(h=0)
abline(v=0)
# 凡例描画
legend("bottomleft", legend=c(f1_name,f2_name,f3_name,f4_name),lty=c(1,1,1,1),col=c(Red,Magenta,Blue,Black))
実例3「y=sin(t)+cos(t)+1/2sin(2t)+1/2cos(2t)+1/3sin(3t)+1/3cos(3t)」

# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル定義
Main_title<-c("Mix of Sine waves ")
x_title<-c("X")
y_title<-c("Y")
# グラフのスケール決定
gs_x<-c(-pi,pi)
gs_y<-c(-3,3)
# y=sin(x)
f1_name<-c("sin(x)")
glaph_y1<-function(x) {sin(x)}
# y=cos(x)
f2_name<-c("cos(x)")
glaph_y2<-function(x) {cos(x)}
# y=1/2*sin(2*x)
f3_name<-c("1/2*sin(2*x)")
glaph_y3<-function(x) {1/2*sin(2*x)}
# y=1/2*cos(2*x)
f4_name<-c("1/2*cos(2*x)")
glaph_y4<-function(x) {1/2*cos(2*x)}
# y=1/3*sin(3*x)
f5_name<-c("1/3*sin(3*x)")
glaph_y5<-function(x) {1/3*sin(3*x)}
# y=1/3*cos(3*x)
f6_name<-c("1/3*cos(3*x)")
glaph_y6<-function(x) {1/3*cos(3*x)}
# y=sin(x)+cos(x)+1/2*sin(2*x)+1/2*cos(2*x)+1/3*sin(3*x)+1/3*cos(3*x)
f7_name<-c("mix of these")
glaph_y7<-function(x) {sin(x)+cos(x)+1/2*sin(2*x)+1/2*cos(2*x)+1/3*sin(3*x)+1/3*cos(3*x)}
# グラフ描画
plot(glaph_y1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(glaph_y2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y4,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y5,xlim=gs_x,ylim=gs_y,type="l",col=Cyan, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y6,xlim=gs_x,ylim=gs_y,type="l",col=Yellow, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_y7,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
# 基準線
abline(h=0)
abline(v=0)
# 凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name,f4_name,f5_name,f6_name,f7_name),lty=c(1,1,1,1,1,1,1),col=c(Red,Magenta,Blue,Green,Cyan,Yellow,Black))
③もっと具体的で著名な波形に挑戦してみる。
ノコギリ波(鋸歯状波(きょしじょうは)、英Sawtooth wave)は非正弦波的な基本的波形の一種で、波形の見た目が鋸の歯のように見えることからそのように呼ばれる。
簡単に説明すれば、その波形は時間と共に上がっていき、急降下するということを繰り返す。もちろん、逆に徐々に下がっていって急上昇することを繰り返すのこぎり波もあり、後者を「逆のこぎり波(英reverse sawtooth wave、inverse sawtooth wave)」と呼ぶ。どちらの波形であってもパラメータを調整すると同じ音に聞こえる。
バーチャルアナログ音源や減算方式などのほとんど全てのシンセサイザーの基本となっている。
ブラウン管などでの画像表示のための走査線を制御する信号の波形である(ラスタースキャン)。
オシロスコープも時系列波形を描く際の水平方向の電子線偏向制御にこれを使っている。
音として聞いてみると、猛々しくハッキリしていて、周波数成分としては基本周波数の偶数倍音と奇数倍音の両方が含まれている。全ての整数倍音を含んでいるため、減算方式のシンセサイザーで、他の音を合成するベースとして使うのに便利である。フーリエ級数を使用して、無限級数の形で理想的な波形を表すことができるが、この表現で興味深いのは矩形波でも起こる「ギブズ現象(Gibbs phenomenon)」である。
Sawtooth_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(0,pi)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/2*x/x},
"1"= f0<-function(x) {pi/2-sin(x*2)},
"2"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2},
"3"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x/6)/3},
"4"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4},
"5"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5},
"6"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6},
"7"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7},
"8"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8},
"9"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9},
"10"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10},
"11"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10-sin(x*22)/11-sin(x*24)/12},
"12"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10-sin(x*22)/11-sin(x*24)/12-sin(x*26)/13-sin(x*28)/14},
"13"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10-sin(x*22)/11-sin(x*24)/12-sin(x*26)/13-sin(x*28)/14-sin(x*30)/15-sin(x*32)/16},
"14"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10-sin(x*22)/11-sin(x*24)/12-sin(x*26)/13-sin(x*28)/14-sin(x*30)/15-sin(x*32)/16-sin(x*34)/17-sin(x*36)/18},
"15"= f0<-function(x) {pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10-sin(x*22)/11-sin(x*24)/12-sin(x*26)/13-sin(x*28)/14-sin(x*30)/15-sin(x*32)/16-sin(x*34)/17-sin(x*36)/18-sin(x*38)/19-sin(x*40)/20}
)
switch(x,
"0"=text<-c("pi/2"),
"1"=text<-c("pi/2-sin(2x)"),
"2"=text<-c("pi/2-sin(2x)-sin(4x)/2"),
"3"=text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3"),
"4"=text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4"),
"5"=text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5"),
"6"=text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12x)/6"),
"7"=text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12x)/6-sin(14x)/7"),
"8"=text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12)/6-sin(14x)/7-sin(16x)/8"),
"9"= text<-c("pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9"),
"10"=text<-c("pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10"),
"11"= text<-c("pi/2-sin(x*2)-sin(x*4)/2-sin(x*6)/3-sin(x*8)/4-sin(x*10)/5-sin(x*12)/6-sin(x*14)/7-sin(x*16)/8-sin(x*18)/9-sin(x*20)/10-sin(x*22)/11-sin(x*24)/12"),
"12"= text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12x)/6-sin(14x)/7-sin(16x)/8-sin(18x)/9-sin(20x)/10-sin(22x)/11-sin(24x)/12-sin(26x)/13-sin(28x)/14"),
"13"= text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12x)/6-sin(14x)/7-sin(16x)/8-sin(18x)/9-sin(20x)/10-sin(22x)/11-sin(24x)/12-sin(26x)/13-sin(28x)/14-sin(30x)/15-sin(32x)/16"),
"14"= text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12x)/6-sin(14x)/7-sin(16x)/8-sin(18x)/9-sin(20x)/10-sin(22x)/11-sin(24x)/12-sin(26x)/13-sin(28x)/14-sin(30x)/15-sin(32x)/16-sin(34x)/17-sin(36x)/18"),
"15"= text<-c("pi/2-sin(2x)-sin(4x)/2-sin(6x)/3-sin(8x)/4-sin(10x)/5-sin(12x)/6-sin(14x)/7-sin(16x)/8-sin(18x)/9-sin(20x)/10-sin(22x)/11-sin(24x)/12-sin(26x)/13-sin(28x)/14-sin(30x)/15-sin(32x)/16-sin(34x)/17-sin(36x)/18-sin(38x)/19-sin(40x)/20")
)
Sawtooth_wave_x<-seq(-pi,pi,length=60)
Sawtooth_wave_y<-rep(seq(0,pi,length=30),times=2)
plot(Sawtooth_wave_x,Sawtooth_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Sawtooth wave", xlab="Frequency", ylab="Amplitude")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
legend("bottomleft", legend=c("f(t)=t-mπ,mπ<=t<(m+1)π",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9","10","11","12","13","14","15")
saveGIF({
for (i in Time_Code){
Sawtooth_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
三角波(Triangular wave)も、非正弦波的な基本的な波形の一種で、波形の見た目が三角形になっているそれ(波形)のことである。無限フーリエ級数で収束。
矩形波と同様に奇数倍音のみを含むが、矩形波に比べて高い倍音成分は急速に小さくなる(倍音の次数の逆数の自乗に比例する)。そのため、矩形波よりも聴きやすく正弦波により近い。回路で生成した三角波をローパスフィルタに通すことで正弦波を得るシンセサイザーもあった。
基本周波数に奇数倍音を合成していくことで三角波の近似を得ることができる。4n−1番目の倍音に−1をかけるか(2m±1)πまたは(2n±1)πによって位相をずらし、基本周波数からの相対周波数の自乗の逆数で振幅を小さくすればよい。
Triangular_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(0,pi/2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/4*x/x},
"1"= f0<-function(x) {pi/4-2*pi/pi^2*cos(2*pi*x/pi)},
"2"= f0<-function(x) {pi/4-2*pi/pi^2*(cos(2*pi*x/pi)+cos(6*pi*x/pi)/3^2)},
"3"= f0<-function(x) {pi/4-2*pi/pi^2*(cos(2*pi*x/pi)+cos(6*pi*x/pi)/3^2+cos(10*pi*x/pi)/5^2)},
"4"= f0<-function(x) {pi/4-2*pi/pi^2*(cos(2*pi*x/pi)+cos(6*pi*x/pi)/3^2+cos(10*pi*x/pi)/5^2+cos(14*pi*x/pi)/7^2)},
"5"= f0<-function(x) {pi/4-2*pi/pi^2*(cos(2*pi*x/pi)+cos(6*pi*x/pi)/3^2+cos(10*pi*x/pi)/5^2+cos(14*pi*x/pi)/7^2+cos(18*pi*x/pi)/9^2)}
)
switch(x,
"0"=text<-c("π/4"),
"1"=text<-c("π/4-2π/π^2*cos(2πx/π)"),
"2"=text<-c("π/4-2π/π^2*(cos(2πx/π)+cos(6πx/π)/3^2)"),
"3"=text<-c("π/4-2π/π^2*(cos(2πx/π)+cos(6πx/π)/3^2+cos(10πx/π)/5^2)"),
"4"=text<-c("π/4-2π/π^2*(cos(2πx/π)+cos(6πx/π)/3^2+cos(10πx/π)/5^2+cos(14πx/π)/7^2)"),
"5"=text<-c("π/4-2π/π^2*(cos(2πx/π)+cos(6πx/π)/3^2+cos(10πx/π)/5^2+cos(14πx/π)/7^2+cos(18πx/π)/9^2)"),
)
Triangular_wave_x<-seq(-pi,pi,length=60)
Triangular_wave_y<-c(seq(0,pi/2,length=15),seq(pi/2,0,length=15),seq(0,pi/2,length=15),seq(pi/2,0,length=15))
plot(Triangular_wave_x,Triangular_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Triangular wave", xlab="Frequency", ylab="Amplitude")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
legend("bottomleft", legend=c("f(t)=t(0=<t<T/2), T-t(T/2<=t<T))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5")
saveGIF({
for (i in Time_Code){
Triangular_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
矩形波(くけいは、Square wave)も、非正弦波的な基本的な波形の一種で、電子工学や信号処理の分野で広く使われている。方形波とも呼ばれる。
理想上は2レベルの間を規則的かつ瞬間的に変化するが、その2レベルにはゼロが含まれることも含まれないこともある。
デジタルスイッチング回路で広く使われており、2進法(2レベル)の論理回路から生成される。厳密に定められた間隔で同期論理回路を動作させるためには矩形波の高速な遷移が適しているので、タイミングの基準や「クロック信号」に使用されている。しかしながら周波数領域グラフからわかるように、矩形波は広帯域の周波数成分を含んでいる。これらは電磁放射や電流のパルスを発生させてしまい、近くの回路に影響を及ぼしその結果、雑音や誤りを引き起こす。精密なAD変換器のような非常に敏感な回路などではこの問題を避けるために、矩形波の代わりに正弦波をタイミング基準として使用する。
フーリエ級数を使用して、無限級数の形で理想的な波形を表すことができるが、この表現で興味深いのは矩形波でも起こる「ギブズ現象(Gibbs phenomenon)」である。のこぎり波でも起こる。
理想的ではない矩形波で生じるリンギングは、この現象と関連している。シグマ近似(sigma-approximation)を用いることで防ぐことができ、系列がより滑らかに収束するように「Lanczos sigma factors」を使うこともできる。
理想的な矩形波には、信号の高値から低値への変化が切れ味よく瞬間的であることが求められるが、そのためには無限の帯域幅が必要となるので、現実の世界での達成は不可能である。
現実の世界には有限の帯域幅しか存在しないため、ギブズ現象に似たリンギングやシグマ近似に似たリップル(電気)が起きることがよくある。
Square_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-1/2,1)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {1/2*x/x},
"1"= f0<-function(x) {1/2+2/pi*sin(x)},
"2"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)},
"3"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)},
"4"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)+2/(7*pi)*sin(7*x)},
"5"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)+2/(7*pi)*sin(7*x)+2/(9*pi)*sin(9*x)},
"6"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)+2/(7*pi)*sin(7*x)+2/(9*pi)*sin(9*x)+2/(11*pi)*sin(11*x)},
"7"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)+2/(7*pi)*sin(7*x)+2/(9*pi)*sin(9*x)+2/(11*pi)*sin(11*x)+2/(13*pi)*sin(13*x)},
"8"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)+2/(7*pi)*sin(7*x)+2/(9*pi)*sin(9*x)+2/(11*pi)*sin(11*x)+2/(13*pi)*sin(13*x)+2/(15*pi)*sin(15*x)},
"9"= f0<-function(x) {1/2+2/pi*sin(x)+2/(3*pi)*sin(3*x)+2/(5*pi)*sin(5*x)+2/(7*pi)*sin(7*x)+2/(9*pi)*sin(9*x)+2/(11*pi)*sin(11*x)+2/(13*pi)*sin(13*x)+2/(15*pi)*sin(15*x)+2/(17*pi)*sin(17*x)}
)
switch(x,
"0"=text<-c("1/2"),
"1"=text<-c("1/2+2/π*sin(x)"),
"2"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)"),
"3"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)"),
"4"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)+2/7π*sin(7x)"),
"5"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)+2/9π*sin(9x)"),
"6"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)+2/9π*sin(9x)+2/11π*sin(11x)"),
"7"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)+2/9π*sin(9x)+2/11π*sin(11x)+2/13π*sin(13x)"),
"8"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)+2/9π*sin(9x)+2/11π*sin(11x)+2/13π*sin(13x)+2/15π*sin(15x)"),
"9"=text<-c("1/2+2/π*sin(x)+2/3π*sin(3x)+2/5π*sin(5x)+2/9π*sin(9x)+2/11π*sin(11x)+2/13π*sin(13x)+2/15π*sin(15x)+2/17π*sin(17x)")
)
Square_wave_x<-seq(-pi,pi,length=60)
Square_wave_y<-c(rep(0,times=30),rep(1,times=30))
plot(Square_wave_x,Square_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Square wave", xlab="Frequency", ylab="Amplitude")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
legend("bottomleft", legend=c("f(t)=0(-π=<t<0), 1(0<=t<π))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Square_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
放物線(希:παραβολή/parabolē、羅/英:parabola、独:Parabel)、すなわちf(t)=t^2(-a<=t<=a)の合成。
信号処理と音楽 放物線形波に対するフーリエ級数展開適用例

Parabola_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-pi/2,pi^2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi^2/3*x/x},
"1"= f0<-function(x) {pi^2/3+4*(-cos(x))},
"2"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2)},
"3"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2)},
"4"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2+cos(4*x)/4^2)},
"5"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2+cos(4*x)/4^2-cos(5*x)/5^2)},
"6"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2+cos(4*x)/4^2-cos(5*x)/5^2+cos(6*x)/6^2)},
"7"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2+cos(4*x)/4^2-cos(5*x)/5^2+cos(6*x)/6^2-cos(7*x)/7^2)},
"8"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2+cos(4*x)/4^2-cos(5*x)/5^2+cos(6*x)/6^2-cos(7*x)/7^2+cos(8*x)/8^2)},
"9"= f0<-function(x) {pi^2/3+4*(-cos(x)+cos(2*x)/2^2-cos(3*x)/3^2+cos(4*x)/4^2-cos(5*x)/5^2+cos(6*x)/6^2-cos(7*x)/7^2+cos(8*x)/8^2)-cos(9*x)/9^2}
)
switch(x,
"0"=text<-c("a^2/3"),
"1"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a))"),
"2"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2"),
"3"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2"),
"4"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2+cos(4πx/a)/4^2"),
"5"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2+cos(4πx/a)/4^2-cos(5πx/a)/5^2"),
"6"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2+cos(4πx/a)/4^2-cos(5πx/a)/5^2+cos(6πx/a)/6^2"),
"7"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2+cos(4πx/a)/4^2-cos(5πx/a)/5^2+cos(6πx/a)/6^2-cos(7πx/a)/7^2"),
"8"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2+cos(4πx/a)/4^2-cos(5πx/a)/5^2+cos(6πx/a)/6^2-cos(7πx/a)/7^2+cos(8πx/a)/8^2"),
"9"=text<-c("a^2/3+4a^2/π^2(-cos(πx/a)+cos(2πx/a)/2^2-cos(3πx/a)/3^2+cos(4πx/a)/4^2-cos(5πx/a)/5^2+cos(6πx/a)/6^2-cos(7πx/a)/7^2+cos(8πx/a)/8^2-cos(9πx/a)/9^2")
)
Parabola_x<-seq(-pi,pi,length=60)
Parabola_y<-Parabola_x^2
plot(Parabola_x,Parabola_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Parabola function", xlab="Frequency", ylab="Amplitude")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
legend("bottomleft", legend=c("f(t)=t^2(-a<=t<=a)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Parabola_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
複素指数関数型フーリエ級数展開の世界
上掲の波形合成の「裏側」が覗けます。
2. 複素指数関数型のフーリエ級数 (やる夫で学ぶディジタル信号処理)
①「三角波(Triangular wave)」や「放物線(Parabola)f(t)=t^2(-a<=t<=a)」の様な「(指数が偶数のCos関数の集合)偶関数系」の場合は、実数領域に波形が顕現する。
②「ノコギリ波(Sawtooth wave)」「矩形波(Square wave)」の様な「(指数が奇数のSin関数の集合)偶関数系」の場合は虚数領域**に波形が顕現する。
偶関数と奇関数の意味,性質などまとめ | 高校数学の美しい物語
三角波(Triangular wave)の場合
library(rgl)
complex_plane_z<-seq(-pi,pi,length=60)
f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2+exp(18*pi*x/pi*(0+1i))/9^2)}
complex_plane_x<-Re(f0(complex_plane_z))
complex_plane_y<-Im(f0(complex_plane_z))
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")
全体像はこうだが実数部を正面にすると確かに三角波が合成されている。

Triangular_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(0,pi/2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/4*x/x},
"1"= f0<-function(x) {pi/4-2*pi/pi^2*exp(2*pi*x/pi*(0+1i))},
"2"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2)},
"3"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2)},
"4"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2)},
"5"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2+exp(18*pi*x/pi*(0+1i))/9^2)}
)
switch(x,
"0"=text<-c("π/4"),
"1"=text<-c("π/4-2π/π^2*exp(2πx/πi)"),
"2"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2)"),
"3"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2)"),
"4"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2+exp(14πx/πi)/7^2)"),
"5"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2+exp(14πx/πi)/7^2+exp(18πx/π)/9^2i)"),
)
# 元波形
Triangular_wave_x<-seq(-pi,pi,length=60)
Triangular_wave_y<-c(seq(0,pi/2,length=15),seq(pi/2,0,length=15),seq(0,pi/2,length=15),seq(pi/2,0,length=15))
plot(Triangular_wave_x,Triangular_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Triangular wave",xlab="t", ylab="Real Number")
par(new=T)#上書き指定
# 実数部
Triangular_wave_yr<-Re(f0(Triangular_wave_x))
plot(Triangular_wave_x,Triangular_wave_yr,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t(0=<t<T/2), T-t(T/2<=t<T))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5")
saveGIF({
for (i in Time_Code){
Triangular_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Triangular_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(0,pi/2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/4*x/x},
"1"= f0<-function(x) {pi/4-2*pi/pi^2*exp(2*pi*x/pi*(0+1i))},
"2"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2)},
"3"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2)},
"4"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2)},
"5"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2+exp(18*pi*x/pi*(0+1i))/9^2)}
)
switch(x,
"0"=text<-c("π/4"),
"1"=text<-c("π/4-2π/π^2*exp(2πx/πi)"),
"2"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2)"),
"3"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2)"),
"4"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2+exp(14πx/πi)/7^2)"),
"5"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2+exp(14πx/πi)/7^2+exp(18πx/π)/9^2i)"),
)
# 元波形
Triangular_wave_x<-seq(-pi,pi,length=60)
Triangular_wave_y<-c(seq(0,pi/2,length=15),seq(pi/2,0,length=15),seq(0,pi/2,length=15),seq(pi/2,0,length=15))
plot(Triangular_wave_x,Triangular_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Triangular wave",xlab="t", ylab="Imaginary Number")
par(new=T)#上書き指定
# 虚数部+定数項
Triangular_wave_yi<-Im(f0(Triangular_wave_x))
plot(Triangular_wave_x,Triangular_wave_yi+pi/4,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t(0=<t<T/2), T-t(T/2<=t<T))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5")
saveGIF({
for (i in Time_Code){
Triangular_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Triangular_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/4*x/x},
"1"= f0<-function(x) {pi/4-2*pi/pi^2*exp(2*pi*x/pi*(0+1i))},
"2"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2)},
"3"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2)},
"4"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2)},
"5"= f0<-function(x) {pi/4-2*pi/pi^2*(exp(2*pi*x/pi*(0+1i))+exp(6*pi*x/pi*(0+1i))/3^2+exp(10*pi*x/pi*(0+1i))/5^2+exp(14*pi*x/pi*(0+1i))/7^2+exp(18*pi*x/pi*(0+1i))/9^2)}
)
switch(x,
"0"=text<-c("π/4"),
"1"=text<-c("π/4-2π/π^2*exp(2πx/πi)"),
"2"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2)"),
"3"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2)"),
"4"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2+exp(14πx/πi)/7^2)"),
"5"=text<-c("π/4-2π/π^2*(exp(2πx/πi)+exp(6πx/πi)/3^2+exp(10πx/πi)/5^2+exp(14πx/πi)/7^2+exp(18πx/π)/9^2i)"),
)
# 基準円
Triangular_wave_x<-seq(-pi,pi,length=60)
plot(cos(Triangular_wave_x)*0.5,sin(Triangular_wave_x)*0.5,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Triangular wave",xlab="Real Number", ylab="Imaginary Number")
par(new=T)#上書き指定
# 複素数波形
Triangular_wave_r<-Re(f0(Triangular_wave_x))
Triangular_wave_i<-Im(f0(Triangular_wave_x))
plot(Triangular_wave_r-pi/4,Triangular_wave_i,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="FT(Fourier transform) Triangular wave",xlab="Real Number", ylab="Imaginary Number")
# 凡例
legend("bottomleft", legend=c("f(t)=t(0=<t<T/2), T-t(T/2<=t<T))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5")
saveGIF({
for (i in Time_Code){
Triangular_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
- 「描画線」が2重に見えるのは2周期分を扱ってるから。
- 2周期分を描画してるから、基準円の半径も1/2としている。
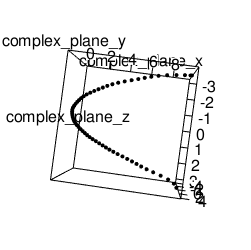
放物線(Parabola)の場合
library(rgl)
complex_plane_z<-seq(-pi,pi,length=60)
f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)-exp(x*9*(0+1i))/9^2}
complex_plane_x<-Re(f0(complex_plane_z))
complex_plane_y<-Im(f0(complex_plane_z))
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")
全体像はこうだが実数部を正面にすると確かに放物線が合成されている。
Parabola_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-pi/2,pi^2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi^2/3*x/x},
"1"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i)))},
"2"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2)},
"3"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2)},
"4"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2)},
"5"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2)},
"6"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2)},
"7"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2)},
"8"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)},
"9"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)-exp(x*9*(0+1i))/9^2}
)
switch(x,
"0"=text<-c("a^2/3"),
"1"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a))"),
"2"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2"),
"3"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2"),
"4"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2"),
"5"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2"),
"6"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2"),
"7"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2"),
"8"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2+exp(8πxi/a)/8^2"),
"9"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2+exp(8πxi/a)/8^2-cos(9πx/a)/9^2")
)
# 元波形
Parabola_x<-seq(-pi,pi,length=60)
Parabola_y<-Parabola_x^2
plot(Parabola_x,Parabola_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Parabola function", xlab="t", ylab="Real Number")
par(new=T)#上書き指定
# 実数部
Parabola_yr<-Re(f0(Parabola_x))
plot(Parabola_x,Parabola_yr,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t^2(-a<=t<=a)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Parabola_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Parabola_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-pi/2,pi^2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi^2/3*x/x},
"1"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i)))},
"2"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2)},
"3"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2)},
"4"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2)},
"5"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2)},
"6"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2)},
"7"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2)},
"8"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)},
"9"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)-exp(x*9*(0+1i))/9^2}
)
switch(x,
"0"=text<-c("a^2/3"),
"1"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a))"),
"2"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2"),
"3"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2"),
"4"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2"),
"5"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2"),
"6"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2"),
"7"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2"),
"8"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2+exp(8πxi/a)/8^2"),
"9"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2+exp(8πxi/a)/8^2-cos(9πx/a)/9^2")
)
# 元波形
Parabola_x<-seq(-pi,pi,length=60)
Parabola_y<-Parabola_x^2
plot(Parabola_x,Parabola_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Parabola function", xlab="t", ylab="Imaginary Number")
par(new=T)#上書き指定
# 虚数部
Parabola_yi<-Im(f0(Parabola_x))
plot(Parabola_x,Parabola_yi+pi^2/3,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t^2(-a<=t<=a)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Parabola_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Parabola_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-2*pi,2*pi)
Graph_scale_y<-c(-2*pi,2*pi)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi^2/3*x/x},
"1"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i)))},
"2"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2)},
"3"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2)},
"4"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2)},
"5"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2)},
"6"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2)},
"7"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2)},
"8"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)},
"9"= f0<-function(x) {pi^2/3+4*(-exp(x*(0+1i))+exp(x*2*(0+1i))/2^2-exp(x*3*(0+1i))/3^2+exp(x*4*(0+1i))/4^2-exp(x*5*(0+1i))/5^2+exp(x*6*(0+1i))/6^2-exp(x*7*(0+1i))/7^2+exp(x*8*(0+1i))/8^2)-exp(x*9*(0+1i))/9^2}
)
switch(x,
"0"=text<-c("a^2/3"),
"1"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a))"),
"2"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2"),
"3"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2"),
"4"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2"),
"5"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2"),
"6"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2"),
"7"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2"),
"8"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2+exp(8πxi/a)/8^2"),
"9"=text<-c("a^2/3+4a^2/π^2(-exp(πxi/a)+exp(2πxi/a)/2^2-exp(3πxi/a)/3^2+exp(4πxi/a)/4^2-exp(5πxi/a)/5^2+exp(6πxi/a)/6^2-exp(7πxi/a)/7^2+exp(8πxi/a)/8^2-cos(9πx/a)/9^2")
)
# 基準円
Parabola_x<-seq(-pi,pi,length=60)
plot(cos(Parabola_x)*pi,sin(Parabola_x)*pi,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform)Parabola wave",xlab="Real Number", ylab="Imaginary Number")
par(new=T)#上書き指定
# 複素数波形
Parabola_r<-Re(f0(Parabola_x))
Parabola_i<-Im(f0(Parabola_x))
plot(Parabola_r-pi^2/3,Parabola_i,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="",xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t^2(-a<=t<=a)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Parabola_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
- 周期は1周期分とした。
- とりあえず対応させる基準円の半径はπとした。
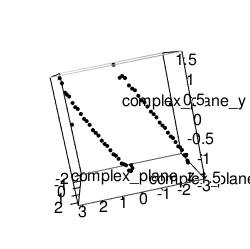
ノコギリ波(Sawtooth Wave)の場合
library(rgl)
complex_plane_z<-seq(-pi,pi,length=60)
f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18-exp(x*38*(0+1i))/19-exp(x*40*(0+1i))/20}
complex_plane_x<-Re(f0(complex_plane_z))
complex_plane_y<-Im(f0(complex_plane_z))
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")
全体像はこうだが虚数部を正面にすると確かにノコギリ波が合成されている。
Sawtooth_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(0,pi)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/2*x/x},
"1"= f0<-function(x) {pi/2-exp(x*2*(0+1i))},
"2"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2},
"3"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3},
"4"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4},
"5"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5},
"6"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6},
"7"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7},
"8"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8},
"9"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9},
"10"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10},
"11"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12},
"12"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14},
"13"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16},
"14"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18},
"15"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18-exp(x*38*(0+1i))/19-exp(x*40*(0+1i))/20}
)
switch(x,
"0"=text<-c("pi/2"),
"1"=text<-c("pi/2-exp(2xi)"),
"2"=text<-c("pi/2-exp(2xi)-exp(4xi)/2"),
"3"=text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3"),
"4"=text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4"),
"5"=text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5"),
"6"=text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6"),
"7"=text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7"),
"8"=text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12)/6-exp(14xi)/7-exp(16xi)/8"),
"9"= text<-c("pi/2-exp(x2i)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(18xi)/9"),
"10"=text<-c("pi/2-exp(x2i)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(18xi)/9-exp(20xi)/10"),
"11"= text<-c("pi/2-exp(x2i)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(18xi)/9-exp(20xi)/10-exp(22xi)/11-exp(24xi)/12"),
"12"= text<-c("pi/2-exp(x2i)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(x*18)/9-exp(20xi)/10-exp(22xi2)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14"),
"13"= text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(18xi)/9-exp(20xi)/10-exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16"),
"14"= text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(18xi)/9-exp(20xi)/10-exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16-exp(34xi)/17-exp(36xi)/18"),
"15"= text<-c("pi/2-exp(2xi)-exp(4xi)/2-exp(6xi)/3-exp(8xi)/4-exp(10xi)/5-exp(12xi)/6-exp(14xi)/7-exp(16xi)/8-exp(18xi)/9-exp(20xi)/10-exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16-exp(34xi)/17-exp(36xi)/18-exp(38xi)/19-exp(40xi)/20")
)
# 元波形
Sawtooth_wave_x<-seq(-pi,pi,length=60)
Sawtooth_wave_y<-rep(seq(0,pi,length=30),times=2)
plot(Sawtooth_wave_x,Sawtooth_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Sawtooth wave", xlab="t", ylab="Real Number")
par(new=T)#上書き指定
# 実数部
Sawtooth_wave_yr<-Re(f0(Sawtooth_wave_x))
plot(Sawtooth_wave_x,Sawtooth_wave_yr,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t-mπ,mπ<=t<(m+1)π",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9","10","11","12","13","14","15")
saveGIF({
for (i in Time_Code){
Sawtooth_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Sawtooth_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(0,pi)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/2*x/x},
"1"= f0<-function(x) {pi/2-exp(x*2*(0+1i))},
"2"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2},
"3"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3},
"4"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4},
"5"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5},
"6"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6},
"7"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7},
"8"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8},
"9"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9},
"10"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10},
"11"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12},
"12"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14},
"13"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16},
"14"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18},
"15"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18-exp(x*38*(0+1i))/19-exp(x*40*(0+1i))/20}
)
switch(x,
"0"=text<-c("pi/2"),
"1"=text<-c("pi/2+exp(2xi)"),
"2"=text<-c("pi/2+exp(2xi)-exp(4xi)/2"),
"3"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3"),
"4"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4"),
"5"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5"),
"6"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6"),
"7"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6-exp(14xi)/7"),
"8"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12)/6+exp(14xi)/7-exp(16xi)/8"),
"9"= text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9"),
"10"=text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10"),
"11"= text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12"),
"12"= text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(x*18)/9-exp(20xi)/10+exp(22xi2)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14"),
"13"= text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16"),
"14"= text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16-exp(34xi)/17-exp(36xi)/18"),
"15"= text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16-exp(34xi)/17-exp(36xi)/18-exp(38xi)/19-exp(40xi)/20")
)
# 元波形
Sawtooth_wave_x<-seq(-pi,pi,length=60)
Sawtooth_wave_y<-rep(seq(0,pi,length=30),times=2)
plot(Sawtooth_wave_x,Sawtooth_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Sawtooth wave", xlab="t", ylab="Imaginary Number")
par(new=T)#上書き指定
# 虚数部+定数項
Sawtooth_wave_yi<-Im(f0(Sawtooth_wave_x))
plot(Sawtooth_wave_x,Sawtooth_wave_yi+pi/2,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=t-mπ,mπ<=t<(m+1)π",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9","10","11","12","13","14","15")
saveGIF({
for (i in Time_Code){
Sawtooth_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Sawtooth_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-pi,pi)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {pi/2*x/x},
"1"= f0<-function(x) {pi/2-exp(x*2*(0+1i))},
"2"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2},
"3"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3},
"4"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4},
"5"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5},
"6"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6},
"7"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7},
"8"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8},
"9"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9},
"10"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10},
"11"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12},
"12"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14},
"13"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16},
"14"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18},
"15"= f0<-function(x) {pi/2-exp(x*2*(0+1i))-exp(x*4*(0+1i))/2-exp(x*6*(0+1i))/3-exp(x*8*(0+1i))/4-exp(x*10*(0+1i))/5-exp(x*12*(0+1i))/6-exp(x*14*(0+1i))/7-exp(x*16*(0+1i))/8-exp(x*18*(0+1i))/9-exp(x*20*(0+1i))/10-exp(x*22*(0+1i))/11-exp(x*24*(0+1i))/12-exp(x*26*(0+1i))/13-exp(x*28*(0+1i))/14-exp(x*30*(0+1i))/15-exp(x*32*(0+1i))/16-exp(x*34*(0+1i))/17-exp(x*36*(0+1i))/18-exp(x*38*(0+1i))/19-exp(x*40*(0+1i))/20}
)
switch(x,
"0"=text<-c("pi/2"),
"1"=text<-c("pi/2+exp(2xi)"),
"2"=text<-c("pi/2+exp(2xi)-exp(4xi)/2"),
"3"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3"),
"4"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4"),
"5"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5"),
"6"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6"),
"7"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6-exp(14xi)/7"),
"8"=text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12)/6+exp(14xi)/7-exp(16xi)/8"),
"9"= text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9"),
"10"=text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10"),
"11"= text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12"),
"12"= text<-c("pi/2+exp(x2i)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(x*18)/9-exp(20xi)/10+exp(22xi2)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14"),
"13"= text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16"),
"14"= text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16-exp(34xi)/17-exp(36xi)/18"),
"15"= text<-c("pi/2+exp(2xi)-exp(4xi)/2+exp(6xi)/3-exp(8xi)/4+exp(10xi)/5-exp(12xi)/6+exp(14xi)/7-exp(16xi)/8+exp(18xi)/9-exp(20xi)/10+exp(22xi)/11-exp(24xi)/12-exp(26xi)/13-exp(28xi)/14-exp(30xi)/15-exp(32xi)/16-exp(34xi)/17-exp(36xi)/18-exp(38xi)/19-exp(40xi)/20")
)
# 基準円
Sawtooth_wave_x<-seq(-pi,pi,length=60)
plot(cos(Sawtooth_wave_x)*0.5,sin(Sawtooth_wave_x)*0.5,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform)Sawtooth wave",xlab="Real Number", ylab="Imaginary Number")
par(new=T)#上書き指定
# 複素数波形
Sawtooth_wave_r<-Re(f0(Sawtooth_wave_x))
Sawtooth_wave_i<-Im(f0(Sawtooth_wave_x))
plot(Sawtooth_wave_r-pi/2,Sawtooth_wave_i,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="FT(Fourier transform)Sawtooth wave",xlab="Real Number", ylab="Imaginary Number")
# 凡例
legend("bottomleft", legend=c("f(t)=t-mπ,mπ<=t<(m+1)π",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9","10","11","12","13","14","15")
saveGIF({
for (i in Time_Code){
Sawtooth_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
- 「描画線**」が2重に見えるのは2周期分を扱ってるから。
- 2周期分を描画してるから、基準円の半径も1/2としている。
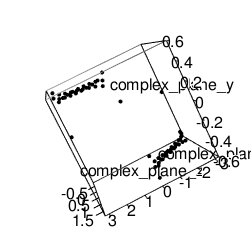
矩形波(Square wave)の場合
library(rgl)
complex_plane_z<-seq(-pi,pi,length=60)
f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))+2/(17*pi)*exp(x*17*(0+1i))}
complex_plane_x<-Re(f0(complex_plane_z))
complex_plane_y<-Im(f0(complex_plane_z))
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")
全体像はこうだが虚数部を正面にすると確かに矩形波が合成されている。

Square_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-1/2,1)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {1/2*x/x},
"1"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))},
"2"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))},
"3"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))},
"4"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))},
"5"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))},
"6"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))},
"7"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))},
"8"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))},
"9"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))+2/(17*pi)*exp(x*17*(0+1i))}
)
switch(x,
"0"=text<-c("1/2"),
"1"=text<-c("1/2+2/π*exp(xi)"),
"2"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)"),
"3"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)"),
"4"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)"),
"5"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)"),
"6"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)"),
"7"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)"),
"8"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)+2/15π*exp(15xi)"),
"9"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)+2/15π*exp(15xi)+2/17π*exp(17xi)")
)
# 元波形
Square_wave_x<-seq(-pi,pi,length=60)
Square_wave_y<-c(rep(0,times=30),rep(1,times=30))
plot(Square_wave_x,Square_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Square wave", xlab="t", ylab="Real Number")
par(new=T)#上書き指定
# 実数部
Square_wave_yr<-Re(f0(Square_wave_x))
plot(Square_wave_x,Square_wave_yr,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=0(-π=<t<0), 1(0<=t<π))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Square_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Square_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-pi,pi)
Graph_scale_y<-c(-1/2,1)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {1/2*x/x},
"1"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))},
"2"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))},
"3"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))},
"4"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))},
"5"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))},
"6"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))},
"7"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))},
"8"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))},
"9"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))+2/(17*pi)*exp(x*17*(0+1i))}
)
switch(x,
"0"=text<-c("1/2"),
"1"=text<-c("1/2+2/π*exp(xi)"),
"2"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)"),
"3"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)"),
"4"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)"),
"5"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)"),
"6"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)"),
"7"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)"),
"8"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)+2/15π*exp(15xi)"),
"9"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)+2/15π*exp(15xi)+2/17π*exp(17xi)")
)
# 元波形
Square_wave_x<-seq(-pi,pi,length=60)
Square_wave_y<-c(rep(0,times=30),rep(1,times=30))
plot(Square_wave_x,Square_wave_y,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform) Square wave", xlab="t", ylab="Imaginary Number")
par(new=T)#上書き指定
# 虚数部+定数項
Square_wave_yi<-Im(f0(Square_wave_x))
plot(Square_wave_x,Square_wave_yi+1/2,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=0(-π=<t<0), 1(0<=t<π))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Square_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
Square_wave_exp<-function(x){
# グラフのスケール決定
Graph_scale_x<-c(-2,2)
Graph_scale_y<-c(-2,2)
# 関数と凡例の決定
switch(x,
"0"= f0<-function(x) {1/2*x/x},
"1"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))},
"2"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))},
"3"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))},
"4"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))},
"5"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))},
"6"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))},
"7"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))},
"8"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))},
"9"= f0<-function(x) {1/2+2/pi*exp(x*(0+1i))+2/(3*pi)*exp(x*3*(0+1i))+2/(5*pi)*exp(x*5*(0+1i))+2/(7*pi)*exp(x*7*(0+1i))+2/(9*pi)*exp(x*9*(0+1i))+2/(11*pi)*exp(x*11*(0+1i))+2/(13*pi)*exp(x*13*(0+1i))+2/(15*pi)*exp(x*15*(0+1i))+2/(17*pi)*exp(x*17*(0+1i))}
)
switch(x,
"0"=text<-c("1/2"),
"1"=text<-c("1/2+2/π*exp(xi)"),
"2"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)"),
"3"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)"),
"4"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)"),
"5"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)"),
"6"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)"),
"7"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)"),
"8"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)+2/15π*exp(15xi)"),
"9"=text<-c("1/2+2/π*exp(xi)+2/3π*exp(3xi)+2/5π*exp(5xi)+2/7π*exp(7xi)+2/9π*exp(9xi)+2/11π*exp(11xi)+2/13π*exp(13xi)+2/15π*exp(15xi)+2/17π*exp(17xi)")
)
# 基準円
Square_wave_x<-seq(-pi,pi,length=60)
plot(cos(Square_wave_x)*0.5,sin(Square_wave_x)*0.5,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="FT(Fourier transform)Square wave",xlab="Real Number", ylab="Imaginary Number")
par(new=T)#上書き指定
# 複素数波形
Square_wave_r<-Re(f0(Square_wave_x))
Square_wave_i<-Im(f0(Square_wave_x))
plot(Square_wave_r-1/2,Square_wave_i,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="",xlab="", ylab="")
# 凡例
legend("bottomleft", legend=c("f(t)=0(-π=<t<0), 1(0<=t<π))",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=c("0","0","0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","6","7","8","9")
saveGIF({
for (i in Time_Code){
Square_wave_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
- とりあえず周期は1周期分とした。
- とりあえず対応させる基準円の半径は1/2とした。
そんな感じで以下続報…


















