pythonのsimpyを使えば簡単に実装できると聞いて試してみました。
Python: ラプラス変換(数式通り実装してみた)
SymPyでラプラス変換
sym.init_printing()はJupyter notebookで数式を表示させる為のおまじないとか。元変換表はこちらから借用。
ラプラス変換 公式一覧
ついでにpytonモジュールの使い方を総合的に解説するPDFを見つけたのでリンク先を貼っておきます。これにはこれからお世話になる局面が増えそうだ?
Python3モジュールブック
そもそもラプラス変換とは何か?
以下を引用しておきます。
ラプラス変換の定義は,時間tの関数をf(t)とすると以下となります。
F(s)=\int_{0}^{\infty} f(t) e^{-st} dt
この式は時間t の関数f(t) にを掛け合わせたものについてt=0から∞まで積分することでtの関数をsの関数F(s)に変換します。式中のsはラプラス演算子といいs>0で複素数も取り得ます(一方tは実数のみ)。ラプラス変換を数式記号を用いて示す場合は次のように記します。
F(s)=\mathcal{L}[f(t)]
ラプラス変換された関数F(s)を時間関数f(t)に再び変換することをラプラス逆変換といい、数式記号を用いて示す場合は次のように記します。
f(t)=\mathcal{L}^{-1}[F(s)]
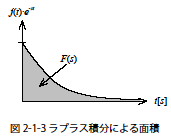
ラプラス変換のイメージを絵的に説明すると,ラプラス変換によって得られるF(s)はf(t)と$e^{-st}$を掛け合わせたものについてt軸に挟まれたt=0から∞までの面積と考えることができます。図のグラフは時間関数 f(t)と$e^{-st}$を掛け合わせたもの(ラプラス積分の中身)について,時間的変化を示していますが、灰色に塗りつぶしている領域の面積がまさにF(s)と等価となります。
f(t)がt→∞で収束していますが、ラプラス変換が成立するにはプラス積分値(F(s))が収束する事が絶対条件で、それを実現する為に$e^{-st}$を掛けているのです。このように収束に起因する因子(ラプラス変換における)を収束因子といいます。ラプラス変換できない例としては,f(t)=exp(t^t)の場合は(exp(x)はexと同じ)ラプラス積分が∞に発散してしまうので,ラプラス変換出来ません。
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=sp.exp(t**t)
Img=sp.laplace_transform(Org, t, s)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
原関数
e^{t^{t}}
像関数
\mathcal{L}_{t}\left[e^{t^{t}}\right]\left(s\right)
フーリエ変換との関係
フーリエ変換/逆変換の公式は以下です。
フーリエ変換
F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t}dt\\
f(t)=\frac{1}{2π} \int_{-\infty}^{\infty} F(\omega) e^{-i \omega t}d\omega
これを以下の様に表します。
F(\omega)=\mathcal{F}[f(t)]\\
f(t)=\mathcal{F}^{-1}[F(\omega)]
よく似て見えますが、実際iω(ωは実数)の部分にs(sは複素数)を代入したのがラプラス変換です(要するに範囲無限を実現する為の方便の違い)。
ラプラス変換
フーリエ変換では、微分演算子はiωに、積分は1/iωに変換される。すなわち、ラプラス変換の変数sは微分演算子に相当する事になる。
- ラプラス変換は指数関数の部分に虚数が付いていない.
- ラプラス変換の式の積分範囲はt>0に限られている.
- ラプラス変換ではsの値は複素数の範囲で考えても良い.(しかしtは実数である)
- ラプラス変換では無理して物理的なイメージを考えない方がいい.
- ラプラス変換の逆変換の式はあるにはあるが,虚数軸に沿った無限積分が必要になる.
ラプラスとフーリエは同じ頃に活躍した人物であるが,ラプラス変換が 1780年頃,フーリエ変換が 1807年頃の発表であり,両者の発想にそれほど深い関わりはないように思われる。
「1」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=1
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
1
像関数
\left( \frac{1}{s}, \ 0, \ \text{True}\right)
再写像
\theta\left(t\right)
「K」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,K = sp.symbols('s,t,K')
w = sp.symbols('w', real=True)
Org=K
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
K
像関数
\left( \frac{K}{s}, \ 0, \ \text{True}\right)
再写像
K \theta\left(t\right)
「t」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=t
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
t
像関数
\left( \frac{1}{s^{2}}, \ 0, \ \text{True}\right)
再写像
t \theta\left(t\right)
「t^n」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=t**n
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
t^{n}
像関数
\left( \frac{s^{- n} \Gamma\left(n + 1\right)}{s}, \ 0, \ \operatorname{re}{\left(n\right)} > -1\right)
再写像
t^{n} \theta\left(t\right)
なるほど、下記をこう表すのがsympy流なのですね。
\frac{n!}{S^{S+1}}
「e^at」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,a = sp.symbols('s,t')
a = sp.symbols('a', real=True)
Org=sp.exp(a*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
e^{a t}
像関数
\left( \frac{1}{- a + s}, \ 0, \ \left|{\arg{\left(a \right)} + \pi}\right| < \frac{\pi}{2}\right)
再写像
e^{t \operatorname{re}{\left(a\right)} + i t \operatorname{im}{\left(a\right)}} \theta\left(t\right)
なるほど、きっちり複素数表現で戻してくるんですね。
「t^n*e^at」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,n = sp.symbols('s,t,n')
a = sp.symbols('a', real=True)
Org=t**n*sp.exp(a*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
t^{n} e^{a t}
像関数
\left( \begin{cases} \frac{a^{- n} \left(-1 + \frac{s}{a}\right)^{- n} e^{i \pi} \Gamma\left(n + 1\right)}{a - s} & \text{for}\: \left|{\frac{s}{a}}\right| > 1 \\\frac{a^{- n} \left(1 - \frac{s}{a}\right)^{- n} e^{i \pi} e^{- i \pi n} \Gamma\left(n + 1\right)}{a - s} & \text{otherwise} \end{cases}, \ 0, \ \left|{\arg{\left(a \right)} + \pi}\right| \leq \frac{\pi}{2} \wedge \operatorname{re}{\left(n\right)} + 1 > 0\right)
再写像
\mathcal{L}^{-1}_{s}\left[\begin{cases} \frac{e^{i \pi} \Gamma\left(n + 1\right)}{a a^{n} \left(-1 + \frac{s}{a}\right)^{n} - a^{n} s \left(-1 + \frac{s}{a}\right)^{n}} & \text{for}\: \left|{\frac{s}{a}}\right| > 1 \\\frac{e^{i \pi} \Gamma\left(n + 1\right)}{a a^{n} \left(1 - \frac{s}{a}\right)^{n} e^{i \pi n} - a^{n} s \left(1 - \frac{s}{a}\right)^{n} e^{i \pi n}} & \text{otherwise} \end{cases}\right]\left(t\right)
ちなみに一般的な変換表での像関数は以下。
\frac{n!}{(S-a)^{n+1}}
「Cos(wt)」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=sp.cos(w*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\cos{\left(t w \right)}
像関数
\left( \frac{s}{s^{2} + w^{2}}, \ 0, \ 2 \left|{\arg{\left(w \right)}}\right| = 0\right)
再写像
\cos{\left(t w \right)} \theta\left(t\right)
「Sin(wt)」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=sp.sin(w*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\sin{\left(t w \right)}
像関数
\left( \frac{w}{s^{2} + w^{2}}, \ 0, \ 2 \left|{\arg{\left(w \right)}}\right| = 0\right)
再写像
\sin{\left(t w \right)} \theta\left(t\right)
「e^at*Cos(bt)」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t = sp.symbols('s,t')
a,b=sp.symbols('a,b',real=True)
Org=sp.exp(α*t)*sp.cos(b*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
e^{t α} \cos{\left(b t \right)}
像関数
\left( \frac{s - α}{b^{2} + \left(s - α\right)^{2}}, \ -\infty, \ 2 \left|{\arg{\left(b \right)}}\right| = 0 \wedge \left|{2 \arg{\left(α \right)} + 2 \arg{\left(- \frac{s}{α} + 1 \right)} + 2 \pi}\right| < \pi\right)
再写像
\frac{\left(e^{i t \left(b + \operatorname{im}{\left(α\right)}\right)} + e^{- i t \left(b - \operatorname{im}{\left(α\right)}\right)}\right) e^{t \operatorname{re}{\left(α\right)}} \theta\left(t\right)}{2}
なるほど、きっちり複素数表現で戻してくるんですね。ちなみに一般的な変換表での像関数は以下。
\frac{S-a}{(S-a)^2+b^2}
「e^at*Sin(bt)」の場合
ラプラス変換
import sympy as sp
s,t = sp.symbols('s,t')
a,b = sp.symbols('a,b', real=True)
Org=sp.exp(α*t)*sp.sin(b*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
e^{t α} \sin{\left(b t \right)}
像関数
\left( \frac{b}{b^{2} + \left(s - α\right)^{2}}, \ -\infty, \ 2 \left|{\arg{\left(b \right)}}\right| = 0 \wedge \left|{2 \arg{\left(α \right)} + 2 \arg{\left(- \frac{s}{α} + 1 \right)} + 2 \pi}\right| < \pi\right)
再写像
- \frac{i \left(e^{i t \left(b + \operatorname{im}{\left(α\right)}\right)} - e^{- i t \left(b - \operatorname{im}{\left(α\right)}\right)}\right) e^{t \operatorname{re}{\left(α\right)}} \theta\left(t\right)}{2}
なるほど、きっちり複素数表現で戻してくるんですね。ちなみに一般的な変換表での像関数は以下。
\frac{b}{(S-a)^2+b^2}
「t*Cos(wt)」の場合
何故か逆変換出来ませんでした。現時点の私には理由が明らかに出来ません。
ラプラス変換/逆変換(原関数→像関数)
import sympy as sp
s,t = sp.symbols('s,t')
w=sp.symbols('w',real=True)
Org=t*sp.cos(w*t)
Img=sp.laplace_transform(Org, t, s)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
原関数
t \cos{\left(t w \right)}
像関数
\left( \frac{s^{2} - w^{2}}{\left(s^{2} + w^{2}\right)^{2}}, \ 0, \ 2 \left|{\arg{\left(w \right)}}\right| = 0\right)
「t*Sin関数」の場合
同じく逆変換出来ませんでした。現時点の私には理由が明らかに出来ません。
ラプラス変換/逆変換(原関数→像関数)
import sympy as sp
s,t = sp.symbols('s,t')
w = sp.symbols('w', real=True)
Org=t*sp.sin(b*t)
Img=sp.laplace_transform(Org, t, s)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
原関数
t \sin{\left(t w \right)}
像関数
\left( \frac{2 s w}{\left(s^{2} + w^{2}\right)^{2}}, \ 0, \ 2 \left|{\arg{\left(w \right)}}\right| = 0\right)
「Cosh(wt)」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=sp.cosh(w*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\cosh{\left(t w \right)}
像関数
\left( \begin{cases} - \frac{s e^{i \pi}}{s^{2} - w^{2}} & \text{for}\: \left|{\frac{s^{2}}{w^{2}}}\right| < 1 \\\frac{s}{s^{2} - w^{2}} & \text{for}\: \frac{1}{\left|{\frac{s^{2}}{w^{2}}}\right|} < 1 \\\frac{\pi {G_{3, 3}^{2, 1}\left(\begin{matrix} \frac{1}{2} & 0, 0 \\0, \frac{1}{2} & 0 \end{matrix} \middle| {\frac{s^{2}}{w^{2}}} \right)}}{w} & \text{otherwise} \end{cases}, \ \max\left(0, \cos{\left(\left|{\arg{\left(w \right)}}\right| \right)} \left|{w}\right|\right), \ 2 \left|{\arg{\left(w \right)}}\right| < \pi \wedge \frac{s^{2}}{w^{2}} \neq 1\right)
再写像
\mathcal{L}^{-1}_{s}\left[\begin{cases} - \frac{s e^{i \pi}}{s^{2} - w^{2}} & \text{for}\: \left|{\frac{s^{2}}{w^{2}}}\right| < 1 \\\frac{s}{s^{2} - w^{2}} & \text{for}\: \frac{1}{\left|{\frac{s^{2}}{w^{2}}}\right|} < 1 \\\frac{\pi {G_{3, 3}^{2, 1}\left(\begin{matrix} \frac{1}{2} & 0, 0 \\0, \frac{1}{2} & 0 \end{matrix} \middle| {\frac{s^{2}}{w^{2}}} \right)}}{w} & \text{otherwise} \end{cases}\right]\left(t\right)
「Sinh(wt)」の場合
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s, t = sp.symbols('s, t')
w = sp.symbols('w', real=True)
Org=sp.sinh(w*t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\sinh{\left(t w \right)}
像関数
\left( \frac{w}{\left(s - w\right) \left(s + w\right)}, \ 0, \ \left(\left|{\arg{\left(w \right)} + \pi}\right| \leq \frac{\pi}{2} \vee \left|{\arg{\left(w \right)} + \pi}\right| < \frac{\pi}{2}\right) \wedge \left(\left|{\arg{\left(w \right)}}\right| \leq \frac{\pi}{2} \vee \left|{\arg{\left(w \right)}}\right| < \frac{\pi}{2}\right)\right)
再写像
\sinh{\left(t w \right)} \theta\left(t\right)
デルタ関数の場合
【数理考古学】ディラックのデルタ関数とヘヴィサイドのステップ関数
定義上はラプラス変換すると1に変換される様です。
ディラックのデルタ関数
とりあえず試したところ、逆変換は出来ませんでした。
ラプラス変換/逆変換(原関数→像関数)
import sympy as sp
s,t = sp.symbols('s,t')
Org=sp.DiracDelta(t)
Img=sp.laplace_transform(Org, t, s)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
原関数
\delta\left(t\right)
像関数
\left( 1 - \theta\left(0\right), \ -\infty, \ \text{True}\right)
ステップ関数の場合
【数理考古学】ディラックのデルタ関数とヘヴィサイドのステップ関数
ラプラス変換(→1/s)もラプラス逆変換(→1)も通ったものの、その振る舞いは完全に「1」そのもの。考えて見ればt=0でswitch onでは仕方がない?
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t = sp.symbols('s,t')
Org=Heaviside(t)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\theta\left(t\right)
像関数
\left( \frac{1}{s}, \ 0, \ \text{True}\right)
再写像
\theta\left(t\right)
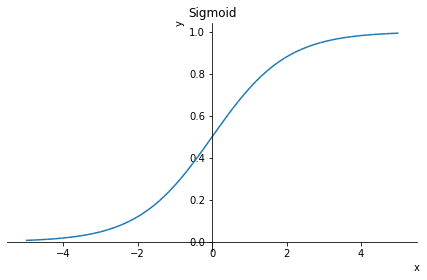
「シグモイド関数1/(1-e^at)」の場合
こういう関数です。
シグモイド関数を調べる(仮)
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
import sympy as sp
import numpy as np
sp.init_printing()
# NumPyによる実装とプロット
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-5.0, 5.0, 100)
y = sigmoid(x)
plt.plot(x,y,color="blue", label="Sigmoid")
plt.title("Sigmoid")
ax.legend(loc='lower right')
plt.show()
# SymPyによる実装とプロット
x,y,dy,ddy = sp.symbols('x,y,dy,ddy')
y = 1 / (1 + sp.exp(-x))
display(y)
print(sp.latex(y))
sp.plotting.plot(y, (x, -5, 5),title="Sigmoid",xlabel = "x", ylabel = "y")
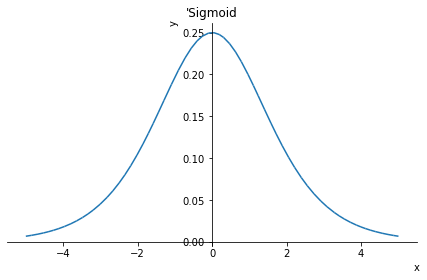
# 1次導関数
dy = sp.diff(y, x, 1)
display(dy)
print(sp.latex(dy))
sp.plotting.plot(dy, (x, -5, 5),title="'Sigmoid",xlabel = "x", ylabel = "y")
# 2次導関数
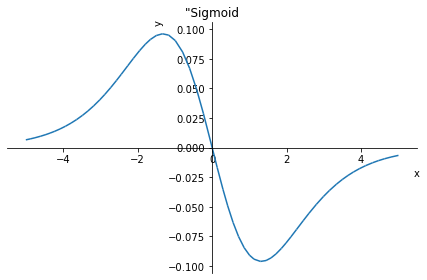
ddy = sp.diff(y, x, 2)
display(ddy)
print(sp.latex(ddy))
sp.plotting.plot(ddy, (x, -5, 5),title="''Sigmoid",xlabel = "x", ylabel = "y")
matplotlibによるプロット例
Sympyによるプロット例
原関数
\frac{1}{1 + e^{- x}}
\frac{e^{- x}}{\left(1 + e^{- x}\right)^{2}}
2次導関数
\frac{\left(-1 + \frac{2 e^{- x}}{1 + e^{- x}}\right) e^{- x}}{\left(1 + e^{- x}\right)^{2}}
一応試してみました。t<0の場合を含むので上手くいかない? 逆変換も出来ませんでした。
ラプラス変換/逆変換(原関数→像関数)
import sympy as sp
s, t = sp.symbols('s,t')
a = sp.symbols('a', real=True)
Org=1/(1+sp.exp(-a*t))
Img=sp.laplace_transform(Org, t, s)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
原関数
\frac{1}{1 + e^{- a t}}
像関数
\mathcal{L}_{t}\left[\frac{1}{1 + e^{- a t}}\right]\left(s\right)
交代級数「-1^n=(0±1i)^2」の場合
実は一般変換表にないこの式をどう処理するのか見たかったのです。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数(Alternating Series)
とりあえず最初から複素数の状態で渡さないと思った反応が得られない事が分かりました。ちなみにSympyでグラフ表示しようとも試みたのですが、エラーが出まくったり、罫線しか表示されなくて挫折。
出発点としての「1^n=(1+0j)^2」の場合
まるで「1」の場合と結果が変わりません。
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=(1+0j)**n
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
1.0^{n}
像関数
\left( \frac{1.0^{n}}{s}, \ 0, \ \text{True}\right)
再写像
1.0^{n} \theta\left(t\right)
交代級数「-1^n=(-1+0j)^n」の場合
「1/1^n」だと負符号が追加されるだけですが、「(-1+0j)^n」はそれらしい動きを見せ始めます。
ラプラス変換/逆変換(原関数→像関数→再写像)
「-1^n」の場合
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=-1**n
sp.plotting.plot(Org,(x,-2,2),(y,-2,2),title="1^n",xlabel = "Real", ylabel = "Imaginal")
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
-1
像関数
\left( - \frac{1}{s}, \ 0, \ \text{True}\right)
再写像
- \theta\left(t\right)
「(-1+0j)^n」の場合
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=(-1+0j)**n
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\left(-1.0\right)^{n}
像関数
\left( \frac{1.0^{n} e^{i \pi n}}{s}, \ 0, \ \text{True}\right)
再写像
1.0^{n} e^{i \pi \operatorname{re}{\left(n\right)} - \pi \operatorname{im}{\left(n\right)}} \theta\left(t\right)
複素円描画関数「(0+1i)^2n」の場合
ここからが本番という感じですね。
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=(0+1j)**(2*n)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
- \left(1.0 i\right)^{2 n}
像関数
\left( - \frac{1.0^{n} e^{i \pi n}}{s}, \ 0, \ \text{True}\right)
再写像
- 1.0^{n} e^{i \pi \operatorname{re}{\left(n\right)} - \pi \operatorname{im}{\left(n\right)}} \theta\left(t\right)
複素円描画関数「(0-1i)^2n」の場合
「え?、負の符号はそこにつくの?」というのが第一印象。
ラプラス変換/逆変換(原関数→像関数→再写像)
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=(0-1j)**(2*n)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
- \left(- 1.0 i\right)^{2 n}
像関数
\left( - \frac{1.0^{n} e^{- i \pi n}}{s}, \ 0, \ \text{True}\right)
再写像
- 1.0^{n} e^{- i \pi \operatorname{re}{\left(n\right)} + \pi \operatorname{im}{\left(n\right)}} \theta\left(t\right)
ところでSympyにはSympy.Iという複素数を扱うオブジェクトが存在するのです。
ラプラス変換/逆変換(原関数→像関数→再写像)
「i^n」の場合
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=sp.I**n
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
i^{n}
像関数
\left( \frac{e^{\frac{i \pi n}{2}}}{s}, \ 0, \ \text{True}\right)
再写像
e^{\frac{i \pi \operatorname{re}{\left(n\right)}}{2} - \frac{\pi \operatorname{im}{\left(n\right)}}{2}} \theta\left(t\right)
「(-i)^n」の場合
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=(-sp.I)**n
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\left(- i\right)^{n}
像関数
\left( \frac{e^{- \frac{i \pi n}{2}}}{s}, \ 0, \ \text{True}\right)
再写像
e^{- \frac{i \pi \operatorname{re}{\left(n\right)}}{2} + \frac{\pi \operatorname{im}{\left(n\right)}}{2}} \theta\left(t\right)
こうなると頻出の「iそのもの」「e^πin」自体がどう変換されるかが気になります。
ラプラス変換/逆変換(原関数→像関数→再写像)
「i」の場合
i自体の扱いは「1」とかと完全に一致。
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=sp.I
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
i
像関数
\left( \frac{i}{s}, \ 0, \ \text{True}\right)
再写像
i \theta\left(t\right)
「e^iπn」の場合
i^nもそうですが、逆変換の時にre(n)-im(n)と変換されるのですね。
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=sp.exp(sp.pi*sp.I*n)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
e^{i \pi n}
像関数
\left( \frac{e^{i \pi n}}{s}, \ 0, \ \text{True}\right)
再写像
e^{i \pi \operatorname{re}{\left(n\right)} - \pi \operatorname{im}{\left(n\right)}} \theta\left(t\right)
微積分の場合
Sympyには遅延評価オブジェクトがあるので少しは期待したのですが…あっけなく蹴散らされてしまいました。変換段階で遅延評価オブジェクトの中身を解かれてしまいます。
微分の場合
import sympy as sp
s,t,n = sp.symbols('s,t,n')
w = sp.symbols('w', real=True)
Org=(-sp.I)**n
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\frac{\partial}{\partial n} a^{n}
像関数
\left( \frac{a^{n} \log{\left(a \right)}}{s}, \ 0, \ \text{True}\right)
再写像
a^{n} \log{\left(a \right)} \theta\left(t\right)
積分の場合
import sympy as sp
s,t,n,a = sp.symbols('s,t,n,a')
w = sp.symbols('w', real=True)
expr=a**n
Org=sp.Derivative(expr, n)
Img=sp.laplace_transform(Org, t, s)
Repro=sp.inverse_laplace_transform(Img[0], s, t)
sp.init_printing()
display(Org)
print(sp.latex(Org))
display(Img)
print(sp.latex(Img))
display(Repro)
print(sp.latex(Repro))
原関数
\int a^{n}\, dn
像関数
\left( \begin{cases} \frac{a^{n}}{s \log{\left(a \right)}} & \text{for}\: \log{\left(a \right)} \neq 0 \\\frac{n}{s} & \text{otherwise} \end{cases}, \ 0, \ \text{True}\right)
再写像
\mathcal{L}^{-1}_{s}\left[\begin{cases} \frac{a^{n}}{s \log{\left(a \right)}} & \text{for}\: \log{\left(a \right)} \neq 0 \\\frac{n}{s} & \text{otherwise} \end{cases}\right]\left(t\right)
つまり以下は手計算するしかない?
ラプラス変換 - EMANの物理数学
ラプラス変換の結果として得られる関数F(s)にはsの変域に制限がある。sが実数である場合について言えば,同様に$\mathcal{L}(e^{at})$にはs>aという制限があるし,$\mathcal {L}(\sin(at))$や$\mathcal{L}(\cos(at))$にはs>0という制限があるし,$\mathcal {L}(\sinh(at))$や$\mathcal{L}(\cosh(at))$にはs>|a|という制限がある.これらは見た目では判断できるようなものでなく,計算をしてみることで分かる.
線形性
\mathcal{L}[\sum_{n}a f(t)] = a \sum_{n}a_n F(s)
ラプラス変換を二つの関数の世界を繋ぐトンネルだとイメージすると、変換前後の世界を結びつける法則がある。一言で言えば「線形性」である.ある関数を定数倍した関数をラプラス変換すると,その関数をラプラス変換したものを定数倍した関数の世界へとたどり着く.
\mathcal{L}[a f(t)] = a \mathcal{L}[f(t)]
また,ある関数と別の関数の和をラプラス変換すると,それぞれの関数をラプラス変換したものの和を取って作った関数の世界へとたどり着く.
\mathcal{L}[f(t)+g(t)] = \mathcal{L}[f(t)] + \mathcal{L}[g(t)]
相似定理
\mathcal{L}[f(at)]→\frac{1}{a} F(\frac{s}{a})
\mathcal{L}[(\frac{1}{a} f(\frac{t}{a})] → F(as)
変数を定数倍した時にどうなるかは「相似法則」と呼ばれている。
\mathcal{L}[f(at)]→\frac{1}{a} F(\frac{s}{a}) (a>0)
\mathcal{L}[(\frac{1}{a} f(\frac{t}{a})] → F(as) (a>0)
これは逆変換をする時にも全く似た形の法則が成り立つ。
\mathcal{L}^-1[F(as)]→\frac{1}{a} f(\frac{t}{a})(a>0)
\mathcal{L}^-1[(\frac{1}{a} F(\frac{s}{a})] → f(as)(a>0)
a>0の条件が抜けてます?
推移則
\mathcal{L}[f(t-a) u(t-a)] → e^{-as} F(s)
\mathcal{L}[e^{at} f(t)] → F(s+a)
元の関数に$e^{at}$を掛けておけば,変換後の変数をaだけずらすことが出来る。これを「像の移動法則」と呼ぶ。
\mathcal{L}[e^{at} f(t)] → F(s-a)
この証明はひときわ簡単なので書いておこう.
\mathcal{L}[e^{at} f(t)] =\int_{0}^{\infty} e^{^at} f(t) e^{-st} dt= \int_{0}^{\infty} f(t) e^{(-a-s)t} dt=F(s-a)
移動の方向が逆なのですが、どういう事?
微分則
\mathcal{L}[\frac{df(t)}{dt}] → sF(s)-f(0)
\mathcal{L}[\frac{d^2 f(t)}{dt^2}] → s^2 F(s)-f(0)-f'(0)
\mathcal{L}[\frac{d^n f(t)}{dt^n}] → s^n F(s)-s^{n-1} -…-sf^{n-2} (0)-sf^{n-1}(0)
\mathcal{L}[-tf(t)] → \frac{dF(s)}{ds}
\mathcal{L}[(-t)^n f(t)] → F^n (s)
微分された関数f'(t)をラプラス変換したものは,変換後の世界では,微分せずに変換した関数F(s)に変数sを掛けることで表現されてしまうのである。-f(0)が余分に付いている辺りがどうもスッキリしないが,それはまぁ,そういうものだから仕方ない。
\mathcal{L}[\frac{df(t)}{dt}] → sF(s)-f(0)
実はこの法則には少し条件があって,$t\to \infty$において$e^{-st}f(t)\to0$となることが必要なのである.この法則を求める過程でその条件を使う必要があるからだ.この法則の導出には部分積分を使えば良くて,それほど難しくはないので省略しよう.
この法則さえ知っていれば$\mathcal{L}\big(e^{at}\big)=1/(s-a)$という関係を導くことは簡単である。
\mathcal{L}[(e^{at})'] = s \mathcal{L}(e^{at})+e^0 = s\mathcal{L}(e^{at})+1
同じ計算は以下の様にも出来る。
\mathcal{L}[(e^{at})'] = \mathcal{L}(a e^{at})+e^0 = a \mathcal{L}(e^{at})
両方の結果を等式で結べばこうなる。
s\mathcal{L}(e^{at})+1 = a \mathcal{L}(e^{at})\\
$\therefore$ (s-a) L(e^{at})=1\\
$\therefore$ L(e^{at})=\frac{1}{s-a}
微分法則が使える条件を満たすためには$e^{-st}e^{at}\to0 (t\to\infty)$でなければならず,そこからs-a>0でなければならないこともちゃんと出てくる。この微分法則を繰り返し用いることで,n階微分した時の法則も導かれる.例えば2階微分について考えよう。
cal L(f'')=s\mathcal{L}(f')-f'(0)=s[sF(s)-f(0)]-f'(0)=s^2 F(s)-sf(0)-f'(0)
繰り返せばどうなるかは想像が付くだろう。
\mathcal{L}[\frac{d^n f(t)}{dt^n}] → s^n F(s)-s^{n-1} -…-sf^{n-2} (0)-sf^{n-1}(0)
積分則
\mathcal{L}[\int_{0}^{t} f(t)dt] → \frac{1}{s} F(s) + \frac{1}{s} f^{-1}(0)
\mathcal{L}[\int_{0}^{t} \int_{0}^{t} \int_{0}^{t} … \int_{0}^{t} f(t)(dt)^n] → \frac{1}{s^n} F(s) + \frac{1}{s^n} f^{-1}(0)+…+\frac{1}{s} f^{-n}(0)
\mathcal{L}[\int_{-\infty}^{t} f(t)dt] → \frac{1}{s}[\int_{-\infty}^{t} f(t)dt] + \frac{1}{s} F(s)
\mathcal{L}[\frac{1}{t} f(t)dt] → \int_{\infty}^{t} F(s)ds
\mathcal{L}[\frac{1}{t^n} f(t)dt] → \int_{0}^{t} \int_{0}^{t} \int_{0}^{t} … \int_{0}^{t} F(s)(ds)^n
ラプラス変換後に変数sを掛ければ微分をしたものをラプラス変換したものに等しいのだから、sで割ってやったものは,積分したものをラプラス変換したものに相当する。まず次のように置こう。
g(t)= \int_{0}^{t} f(x)ds
すると,g'(t)=f(t)という関係になっている.そこで微分法則を次のように使えば良い.
\mathcal{L}(g')= s \mathcal{L}(g)-g(0)=s\mathcal{L}(g)=s\mathcal{L}(\int_{0}^{t} f(x)ds)
ここから次の法則がいえる。
\mathcal{L}(\int_{0}^{t} f(x)ds)=\frac{1}{s}\mathcal{L}(f)
微分法則とは違ってこちらには余計な項が出てこなくて気持ちいいが,それは積分範囲を0からtまでに設定することでうまくスッキリ見せているだけである。
合成積則
\mathcal{L}[\int_{0}^{t} f_1(t- \tau) f_2 (\tau) d \tau] → F_1(s)F_2(s)
\mathcal{L}[f_1(t)f_2(t)] → \frac{1}{2 \pi j} \int_{B_r} F_1(s-a) F_2(\delta)d \delta
パラメータによる微分則
\mathcal{L}[\frac{\partial}{\partial n} f(t,a)] → \frac{\partial}{\partial n} F(s,a)
パラメータによる積分則
\mathcal{L}[\int_{a}^{b} f(t,a)da] → \int_{a}^{b} F(s,a)da
パラメータによる極限則
\mathcal{L}[\lim_{a \to b} f(t,a)] → \lim_{a \to b} F(t,s)
積分対応式
\mathcal{L}[ \int_{0}^{t} \frac{1}{t} f(t)dt ] → \frac{1}{s} \int_{s}^{\infty} F(s)ds
\mathcal{L}[ \int_{t}^{\infty} \frac{1}{t} f(t)dt ] → \frac{1}{s} \int_{0}^{s} F(s)ds
積分等式
\mathcal{L}[ \int_{0}^{\infty} f(t)dt ] → [F(s)]^{\infty}_0
\mathcal{L}[ \int_{0}^{\infty} \frac{1}{t} f(t)dt ] → \int_{0}^{\infty} F(s)ds
初期値定理
\mathcal{L}[ \lim_{t \to 0} f(t) → \lim_{s \to \infty} sF(s) ]
最終値定理
\mathcal{L}[ \lim_{t \to \infty} f(t) ] → \lim_{s \to 0} sF(s)
そんな感じで以下続報…