シグモイド関数を調べる（仮）

　Pythonでシグモイド関数
$$ f(x) = \frac{1}{1+\exp (-x)} $$
について調べます。

　はじめにNumPyで実装しプロットしてみます。

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-5.0, 5.0, 100)
y = sigmoid(x)
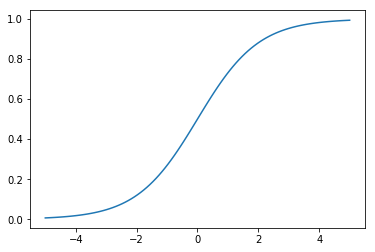
plt.plot(x,y)
plt.show()

0から1の間で単調に増加する形状になります。

SymPyでシグモイド関数を調べる

　関数の形を理解するためには微分をする必要があります。SymPyを使うと解析解を求めつつ簡単にグラフ化できます。

%matplotlib inline
import matplotlib.pyplot as plt
import sympy as sym
sym.init_printing()

Jupyter notebookで数式を表示させるために、sym.init_printing()を実行します。シグモイド関数をプロット後、１次導関数、２次導関数を求めます。

x, y, dy, ddy = sym.symbols('x y dy ddy')
y = 1 / (1 + sym.exp(-x))

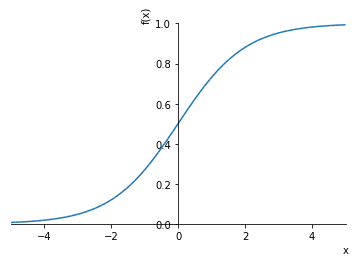
sym.plotting.plot(y, (x, -5, 5))

##1次導関数

dy = sym.diff(y, x, 1)
dy

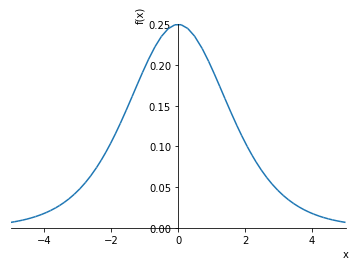
$$\frac{e^{- x}}{\left(1 + e^{- x}\right)^{2}}$$

sym.plotting.plot(dy, (x, -5, 5))

##2次導関数

ddy = sym.diff(y, x, 2)
ddy

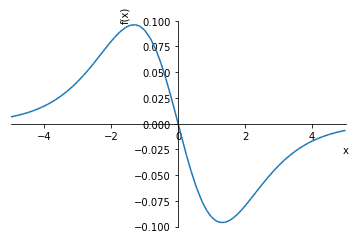
$$\frac{e^{- x}}{\left(1 + e^{- x}\right)^{2}} \left(-1 + \frac{2 e^{- x}}{1 + e^{- x}}\right)$$

sym.plotting.plot(ddy, (x, -5, 5))