今日のネット上では、むしろ「Log(-1)の解は何か?」といった話題で登場する様です。
log(-1)=?
- 底がeの自然対数関数$y=\log(x)$は、自然指数関数$y=e^x$の逆関数として定義されている($x=e^y→y=\log(x)$)。すなわちlog(-1)の解を求めるという事は$e^x=-1$のxを求めるのと同値である。
- オイラーの等式(Eulerian Identity)$e^{πi}=-1$よりx=πi。ただし2π周期の週回数nだけ解が存在する多価関数(Multivalued Function)なので実際の解はπi+2πnとなる。
なるほど、世間一般では$y=-1^x→y=i^{2x}$と考える代わり、こう考える流儀が広まっていたのですね。まぁ辿り着く先は一緒なのです。
-
代数学における虚数$i^2=-1$概念の発見自体は16世紀(カルダーノ「アルス・マグナ(偉大なる術=羅Ars magna de Rebus Algebraicis,1545年)出版」) にまで遡ります。
【数理考古学】三次方程式から虚数へ。 -
一方、解析学史上にこれが現れるのは、以下の交代級数(Alternating Series)概念が登場して以降となるのです。
交項級数 - Wikipedia
\sum_{n=1}^{∞}-1^{n-1}A_n(for ∀n,A_n≧0.[resp.An≦0.])=A_0-A_1+A_2-A_3+…
- 複素平面概念のなかった当時、これを円軌道の一部と認識するのは大変困難でしたが、次第にπや対数/指数との関係が明らかになっていきます。
オイラーの公式(Eulerian Formula)e^θi=cos(θ)+sin(θ)iは一日にしてなった訳ではなかったのですね。
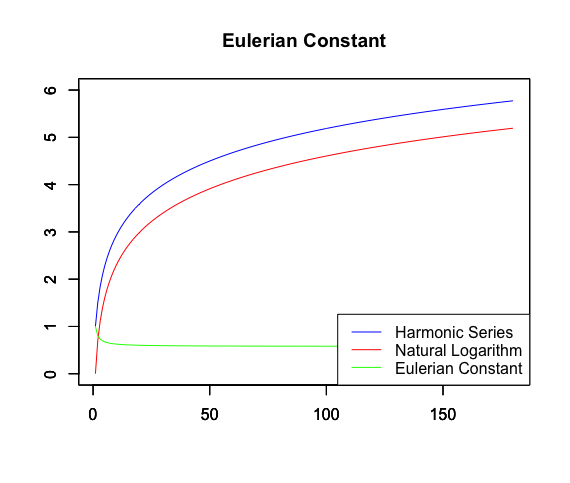
調和級数(harmonic series)の場合
以下の調和級数(harmonic series)が発散する事は既に14世紀には知られていたが、当時の証明は間違っていた事が17世紀に発見され再証明される。
\sum_{n=1}^{∞}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}…
その増え方は極限において対数関数に等しい(18世紀におけるオイラーの発見)。
【数理考古学】オイラー定数の求め方
ニュートン・メルカトル級数(Newton-Mercator Series,1668年)の場合
交代級数概念の最初期登場例の一つ。
メルカトル級数 | Fukusukeの数学めも
\displaystyle \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\log{2}
以下のニュートン・メルカトル級数(Newton-Mercator Series,1668年)の登場は、まさしくlog(2)を巡る諸概念の出発地点となったのです。
log2に収束する交代級数の証明 | 高校数学の美しい物語
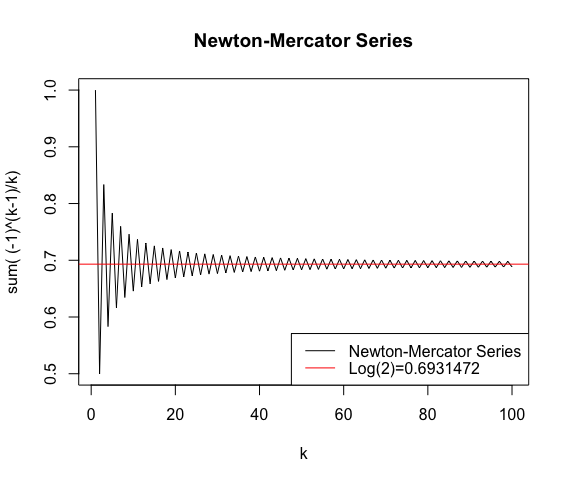
f0<-function(k) (-1)^(k-1)/k
cx<-1:100
cy<-Reduce(function(a,b){a+f0(b)},cx,accumulate = T)
plot(cx,cy,type="l",main="Newton-Mercator Series",xlab="k",ylab="sum( (-1)^(k-1)/k)")
abline(h=log(2),col=rgb(1,0,0))
legend("bottomright", legend=c("Newton-Mercator Series","Log(2)=0.6931472"),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
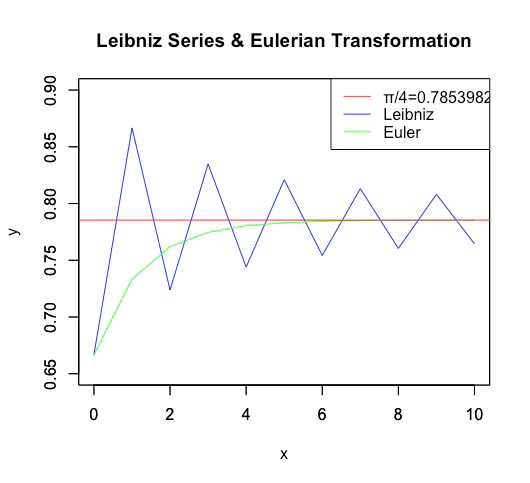
ライプニッツ級数(Leibniz Series,1674年)/グレゴリー級数(Gregory Series,1671年)の場合
これも交代級数概念の最初期登場例の一つ。どちらも円周率計算を巡るArcTangent研究競争の産物であったのです。
【数理考古学】とある円周率への挑戦?
ライプニッツ級数(Leibniz Series,1674年)
ライプニッツ級数 | Fukusukeの数学めも
\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\frac{\pi}{4}
f0<-function(n) ((-1)^n)/(2*n+1)
cx<-c(1,1:99)
cy<-Reduce(function(a,b){a+f0(b)},cx,accumulate = T)
plot(cx,cy,type="l",main="Leibniz Series",xlab="k",ylab="sum(((-1)^n)/(2n+1))")
abline(h=pi/4,col=rgb(1,0,0))
legend("bottomright", legend=c("Leibniz Series","π/4=0.7853982"),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
グレゴリー級数(Gregory Series, 1671年)
グレゴリー級数 | Fukusukeの数学めも
\tan^{-1}x=\sum_{n=0}^{\infty}\frac{(-1)^n}{2n+1}x^{2n+1}=x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots

x=1の時、ライプニッツ級数と一致。収束速度はかなり遅いが、オイラー変換(Eulerian Transformation)によって加速する事が可能。
こうした級数の研究からテイラー級数 (Taylor Series,1715年)やマクローリン級数 (Maclaurin Series,18世紀) が発明され、オイラーの公式(Eulerian Formula)$e^{θi}=cos(θ)+sin(θ)i$発見に結びつく。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?
2^nによる正の実数全表示とlog(2)による全対数表示の対応
ところでlog(x)のテイラー/マクリーン展開は(特異点0の存在がある為に)難しいのですが、幸にして任意の(すべての)正の実数は全て$α2^n$(1≦α<2;nは整数)の形に表せます(ただしここにlog(3,base=2)概念が混ざり込む)。
| Values | Explessions | |
|---|---|---|
| 1 | 1 | 2^0 |
| 2 | 2 | 2^1 |
| 3 | 3 | 2^0+2^1 / 2^log(3,base=2) |
| 4 | 4 | 2^2 |
| 5 | 5 | 2^2+2^0 |
| 6 | 6 | 2^2+2^1 |
| 7 | 7 | 2^2+2^log(3,base=2) |
| 8 | 8 | 2^3 |
1を2の累乗数で割って行くと、小数には、位取り記数法の基数の半分の数が、累乗数として現れる。例えば、十進法の位取り(十進数)では、1を2の累乗数で割っていくと、小数には5の累乗数が現れる。
十進数:
1÷2=0.5(5^1)
1÷4=0.25(5^2)
1÷8 =0.125(5^3)
1÷16=0.0625(5^4)これは$2^{-n}5^{-n}=10^{-n}$より$2^{-n}=5^n10^{-n}$であることから導かれる。
同じく、十二進数では6の累乗数が、二十進数では十の累乗数が現れる。
十二進数:
1÷2=0.6(6^1)
1÷4=0.30(6^2)
1÷8=0.160(6^3)
1÷14=0.0900(6^4)1以外の2の冪2nを十進法で表したとき、一の位は 2, 4, 6, 8 のいずれかである。
1以外の2の冪2nを二進法で表した時は、一番上の位は1であとに0がn個続く数になる。
その(自然)対数をとれば$\log(α2^n)=log(α)+n log(2)$と示せます。つまりlog(2)の値さえ予め求めておけば,ここで示した近似式を用いて任意の正の実数xの自然対数log(x)の値を計算出来る訳です。
対数関数のテイラー展開
| Numbers | Explessions | Values | |
|---|---|---|---|
| 1 | log(1) | log(2^1)+log(1/2) | 0 |
| 2 | log(2) | log(2^1) | 0.6931472 |
| 3 | log(3) | log(3/2)+log(2^1) | 1.098612 |
| 4 | log(4) | log(2^2) | 1.386294 |
| 5 | log(5) | log(5/4)+log(2^2) | 1.609438 |
| 6 | log(6) | log(3/2)+log(2^2) | 1.791759 |
| 7 | log(7) | log(7/4)+log(2^2) | 1.94591 |
| 8 | log(8) | log(2^3) | 2.079442 |
複利計算における「倍増年(元利合計が2倍になる年数)」の近似計算にもlog(2)が現れる。元金をX(>0)、年利率をr(>0)とし、n年後に元利合計が2倍になるとすれば以下である。
$X(1+r)^n=2X$
この両辺の自然対数をとると
n×log(1+r)=log(2)
$n=\frac{log(2)}{log(1+r)}$ここで、r≪1、すなわちcolor=green>rが1に比べて十分に小さい場合には、log(1+r)≒rと近似できるので以下となる。
$n≒≠\frac{log(2)}{r}≒\frac{0.693}{r}$
すなわち「倍増年」は「0.693を年利で割った値」又は「69.3を年利(%表示)で割った値」で近似できる。実用上は、69.3を切りの良い70や約数の多い72で置き換えることが多い。たとえば、年利が3%ならば、72÷3=24なので約24年後に元利合計が倍増する。この法則は、72の法則と呼ばれ、15世紀イタリアにおいて既に知られていた。
文献上の初出は、イタリアの数学者で「会計の父」とも呼ばれるルカ・パチョーリの「スムマ(Summa de arithmetica, geometria, proportioni et proportionalità=算術・幾何・比及び比例全書, 1494年)」』と呼ばれる数学書である。この著作の出版を契機に欧州にも(地中海交易に使われていた)複式簿記が広まった。
ここで元手を1と置いて$(1+r)^n=2$、r=1,n=1.0の場合に$(1+1)^1=2$、さらにこれを初期状態として$r=\frac{1}{n}$と置くとそれはベルヌーイがネイピア数を算出した$(1+\frac{1}{n})^n$の式型となり、さらに$(1+\frac{πi}{n})^n$と置くとオイラーの公式となる。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

- 冪乗算(Exponentiation)の微分x^a'=ax^(a-1)を実際にはa^x*log(x)で求めるのも、上掲の理論に従っての事である。何しろ,以下の定積分を計算するとβ=-1の時、すなわち$x^β=x^{-1}=\frac{1}{x}$の時、右肩の分母が0になって計算不能となってしまう。
\int_{a}^{b}x^βdx=\frac{1}{β+1}b^{β+1}-\frac{1}{β+1}a^{β+1}
計算的には反比例関数y=1/xにおける区間1→2の定積分を求めるのと同じで、この答えもまたLog(2)である。
【数理考古学】冪乗算の微積分 - Qiita
-
テイラー級数展開出来ない複素関数を表示する場合に利用されるローラン級数(Laurent series=負冪の項も含む形での冪級数としての無限関数列,1843年)が開発されたのも、かかる「特異点(Singularity)問題」を回避する為だった。
ローラン級数のテイラー展開を試す。
そう「人工知能が2040年代には人間の知能を超えるかもしれない」と指摘して世間を騒がせている「シンギュラシティ(技術的特異点)問題」の「特異点」とは、この「超えられない壁」を表す数学用語からの援用だったのですね。
特異点
重力の特異点 - Wikipedia
裸の特異点 - Wikipedia
という事は逆に言えば「人工知能は人間の知能を決して超えられない」証明になってしまう?

