前回の投稿では「実数族(Real Family)」なる大分類を想定し、それに下属する(部分集合を構成する)整数族(Integer Family)の概念について考察しました。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
こちらで最初に足掛かりとしたのは加減算に立脚する「(小学校の時に習った)等差数列」でした。今回足掛かりとするのは、同じく小学校の時に習った「乗除算に立脚する等比数列」と冪乗算となります。とはいえ…
等比数列…α=初項(First Ratio),r=公比(Common Rattio)
α^n(n=-Inf(inity)→0→α×r^{n-1},…,+Inf(inity))
冪乗算…α=根(Base,Root)
α^n(n=-Inf(inity)→0→+Inf(inity))=(-Inf(inity),…,α^{-x}=\frac{1}{α^x},…,α^{-1}=\frac{1}{α},α^{0}=\frac{α}{α}=1,α,α^2,α^3,…,+Inf(inity))
Rによる等比数列と等差数列の比較
c0<-seq(-5,5,length=11)
# 等差数列(Arithmetic Sequence=算術数列)
fa<-function(a,d,n){a+d*(n-1)}
# 等比数列(Geometric Sequence=幾何数列)
fg<-function(a,r,n){a*r^(n-1)}
# 等差数列は初項1、公差1の時
# 整数集合の添字と演算結果集合が一致する。
> c0
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
> fa(1,1,c0)
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
# 等差数列で初項1で公差0の時と
# 等比数列で初項0で公比0の時は
# 演算結果集合がy=0で一致する。
> fg(1,0,c0)
[1] 0 0 0 0 0 0 0 0 0 0 0
> fa(0,0,c0)
[1] 0 0 0 0 0 0 0 0 0 0 0
# 等比数列は理論上
# 初項0,公比0の時もy=0に到達するが
# コンピューターはちゃんと計算してくれない。
> fg(0,0,c0)
[1] NaN NaN NaN NaN NaN NaN 0 0 0 0 0
> 0*0^(1-1)
[1] 0
> 0*0^(0-1)
[1] NaN
> 0*0^0
[1] 0
> 0*0^-1
[1] NaN
> 0^-1
[1] Inf
> 0^-2
[1] Inf
> 0^-3
[1] Inf
> 0^-4
[1] Inf
> 0^Inf
[1] 0
# 指数関数0^xの場合は逆に無限大に到達する。
> 0^c0
[1] Inf Inf Inf Inf Inf 1 0 0 0 0 0
# 形式的に等比数列の一般項の対数をとると
# log(αn)=log(a)+(n-1)×log(r)となり
# 初項log(a),公差log(r)の等差数列と一致する。
fgl<-function(a,r,n){log(a)+(n-1)*log(r)}
> fgl(1,2,c0)
[1] -4.1588831 -3.4657359 -2.7725887 -2.0794415 -1.3862944 -0.6931472 0.0000000 0.6931472
[9] 1.3862944 2.0794415 2.7725887
> fa(log(1),log(2),c0)
[1] -4.1588831 -3.4657359 -2.7725887 -2.0794415 -1.3862944 -0.6931472 0.0000000 0.6931472
[9] 1.3862944 2.0794415 2.7725887
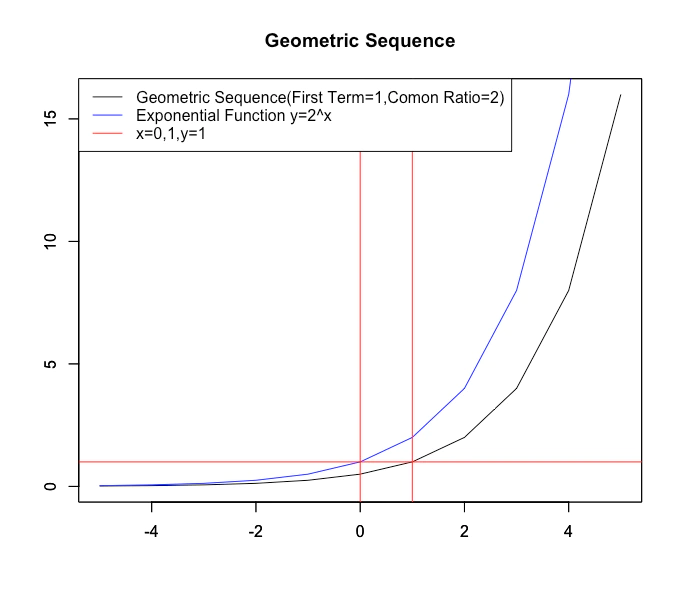
# ちなみに等比数列(初項1,公比2)と指数関数2^xは添字が一つズレている。
> fg(1,2,c0)
[1] 0.015625 0.031250 0.062500 0.125000 0.250000 0.500000 1.000000 2.000000 4.000000
[10] 8.000000 16.000000
> 2^c0
[1] 0.03125 0.06250 0.12500 0.25000 0.50000 1.00000 2.00000 4.00000 8.00000 16.00000
[11] 32.00000
> 2^(c0-1)
[1] 0.015625 0.031250 0.062500 0.125000 0.250000 0.500000 1.000000 2.000000 4.000000
[10] 8.000000 16.000000
そう等差数列における奇数集合同様、例えば等比数列(初項1,公比2)と指数関数2^xも添字が一つズレるのです。
# 等比数列(初項1,公比2)と指数関数2^x+1の比較
plot(c0,fg(1,2,c0),xlim=c(-5,5),type="l",ylim=c(0,16),main="Geometric Sequence",xlab="",ylab="")
par(new=T)
plot(c0,2^c0,xlim=c(-5,5),type="l",ylim=c(0,16),main="",xlab="",ylab="",col=rgb(0,0,1))
abline(v=1,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
abline(h=1,col=rgb(1,0,0))
# 凡例を書き添える 。
legend("topleft", legend=c("Geometric Sequence(First Term=1,Comon Ratio=2)","Exponential Function y=2^x","x=0,1,y=1"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(0,0,1),rgb(1,0,0)))
どうやら等差数列同様、この辺りが頑張れる限界の模様ですね。
2.ネイピア族(Napier Famiry)の定義。
ここでまさかの人名推戴。「指数族」や「指数族」だと演算のイメージが強過ぎて元(Element)っぽくないので、あえてここで「常用対数表の父」に登場してもらう事にした次第です。
ジョン・ネイピア(John Napier,1550年~1617年) - Wikipedia
実際、この族の共通元は前回定義した「整数集合」の以下の写像となります。
-Inf(ity)→0\\
0→1\\
+Inf(ity)→+Inf(ity)
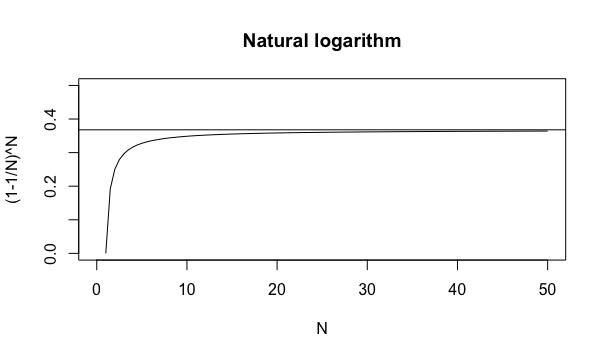
すると-1や+1は一体何処へ行ってしまうのでしょう? もはや近似でしか計算出来ません。概ね1の場合は2(1+1)から、-1の場合は0(1-1)から計算を始めます。
1→exp(1)=(1+\frac{1}{n})^n=2.718282
# ヤコブ・ベルヌイの複利計算法に基づく算出方法
f0=function(x){(1+1/x)^x}
# グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,3),lty =1,main="Natural logarithm", xlab="N", ylab="(1+1/N)^N")
# 自然対数eと比較。
abline(h=exp(1))#exp(1)=2.718282...
-1→exp(-1)=(1-\frac{1}{n})^n=0.3678794
# オイラーの「ネイピアの対数表」に基づく算出方法
f0=function(x){(1-1/x)^x}
# グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,0.5),lty =1,main="Natural logarithm", xlab="N", ylab="(1-1/N)^N")
# 自然対数1/eと比較。
abline(h=exp(-1))#exp(-1)=0.3678794...
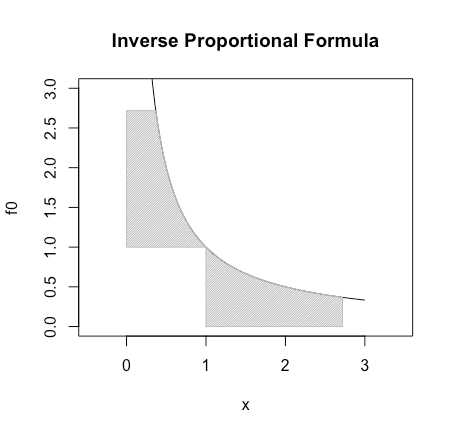
exp(1)とexp(-1)は当然逆数の関係にあり、反比例関数y=1/x上において「1×1の区画の次に面積が1となる座標の組み合わせ」としても知られています。
f0<-function(x){1/x}
plot(f0,asp=1,xlim=c(0,3),ylim=c(0,3),main="Inverse Proportional Formula")
# 該当箇所の塗り潰し
sqx0<-seq(1,exp(1),length=11)
sqy0<-f0(sqx0)
polygon(
c(1,sqx0,exp(1)), #x
c(0,sqy0,0), #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
sqx1<-seq(exp(-1),1,length=11)
sqy1<-f0(sqx1)
polygon(
c(0,0,exp(-1),sqx1,0), #x
c(1,exp(1),exp(1),sqy1,1), #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
全体としてネイピア数exp(1)=2.718282を根とする冪乗算と計算結果が一致し、これを自然指数関数(Natural Exponential Function)exp(x)、その逆関数を自然対数関数(Natural Logarithm Function)log(x)と呼びます。全ての冪乗算は根の変換式によってこれに変換可能なので、族としての元はあくまで一つと考えて良いでしょう。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。
log(a,base=b)=\frac{log(b,base=e)}{log(a,base=e)}
Rによる実装例
log(2,base=3)
[1] 0.6309298
log(2,base=4)/log(3,base=4)
[1] 0.6309298
> log(2)/log(3)
[1] 0.6309298
この対数尺の素晴らしいところは(射影元の整数族の尺度たる)均等尺上における掛け算が足し算に、割り算が引き算に、冪乗算が掛け算に置き換わる事です。近世におけるこの発見と常用対数表の登場により数学者や天文学者や物理学者の寿命が倍増したという話も。
【数理考古学】常用対数表を使った計算
Rによる計算例 1.43*5.93(掛け算→足し算)
> 1.43*5.93
[1] 8.4799
> log(1.43,base=10)
[1] 0.155336
> log(5.93,base=10)
[1] 0.7730547
> log(1.43,base=10)+log(5.93,base=10)
[1] 0.9283907
> 10^0.9283907
[1] 8.479899
pythonによる計算例 1.43*5.93(掛け算→足し算)
import numpy as np
print(1.43*5.93)
print(np.log10(1.43))
print(np.log10(5.93))
a=np.log10(1.43)+np.log10(5.93)
print(a)
print(10**a)
# 出力結果
8.479899999999999
0.1553360374650618
0.7730546933642626
0.9283907308293244
8.4799
Rによる計算例 1.43/5.93(割り算→引き算)
> 1.43/5.93
[1] 0.2411467
> log(1.43,base=10)
[1] 0.155336
> log(5.93,base=10)
[1] 0.7730547
> log(1.43,base=10)-log(5.93,base=10)
[1] -0.6177187
> 10^-0.6177187
[1] 0.2411467
pythonによる計算例 1.43/5.93(割り算→引き算)
import numpy as np
print(1.43/5.93)
print(np.log10(1.43))
print(np.log10(5.93))
a=np.log10(1.43)-np.log10(5.93)
print(a)
print(10**a)
# 出力結果
0.2411467116357504
0.1553360374650618
0.7730546933642626
-0.6177186558992007
0.24114671163575047
Rによる計算例 1034*2213(掛け算→足し算)
> 1034*2213
[1] 2288242
> log(1034,base=10)
[1] 3.014521
> log(2213,base=10)
[1] 3.344981
> log(1034,base=10)+log(2213,base=10)
[1] 6.359502
> log(1034*2213,base=10)
[1] 6.359502
> 10^6.359502
[1] 2288242
pythonによる計算例 1034*2213(掛け算→足し算)
import numpy as np
print(1034*2213)
print(np.log10(1034))
print(np.log10(2213))
a=np.log10(1034)+np.log10(2213)
print(a)
print(10**a)
# 出力結果
2288242
3.0145205387579237
3.344981413927258
6.359501952685182
2288242.000000003
Rによる計算例 1034/2213(割り算→引き算)
> 1034/2213
[1] 0.467239
> log(1034,base=10)
[1] 3.014521
> log(2213,base=10)
[1] 3.344981
> log(1034,base=10)-log(2213,base=10)
[1] -0.3304609
> log(1034/2213,base=10)
[1] -0.3304609
> 10^-0.3304609
[1] 0.467239
pythonによる計算例 1034/2213(割り算→引き算)
import numpy as np
print(1034/2213)
print(np.log10(1034))
print(np.log10(2213))
a=np.log10(1034)-np.log10(2213)
print(a)
print(10**a)
# 出力結果
0.46723904202440125
3.0145205387579237
3.344981413927258
-0.3304608751693343
0.4672390420244012
全体像を俯瞰すると中心の特異点0に向けて無限沈降を続けるブラックホールのイメージ。
【Rで球面幾何学】等比数列(幾何数列)②同心円集合(Concentric Set)に射影(Projection)する準備

しかし最新の科学に拠れば、実際のブラックホールは真逆に円周に対して無限沈降を続ける特異点がある様に見えるとされています。(実際の特異点たる)球面上の対蹠が、重力レンズ効果によって円周に射影されるイメージ…
【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。

ここで興味深いのが、この考え方だと0を演算原点とする演算が特異点(演算極限)1に無限に辿り着けない様に、(この場合に演算極限として現れる)1を演算原点とする演算もまた特異点(演算極限)0に無限に辿り着けない辺り。もしかしたら哲学の世界における「彼我問題(主観と客観が永遠に交わらない問題)」に対応?
【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。

この様に偶奇性(Parity)の概念はまさにかかる「彼我関係(He(She) and I RelationshipあるいはThey and we Relationship)」に由来するのです。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ


【Python演算処理】単位球面を巡る数理②そして単位トーラスへ



ここで重要なのが、その関係が連鎖(反復)するという認識?
ネイピア族(Napier Famiry)の実数への漸近戦略。
しかし問題も生じました。冪乗算の定積分の式は素直に導出すると以下なのですが…
\int_{a}^{b}x^βdx=\frac{1}{β+1}×b^{β+1}-\frac{1}{β+1}×a^{β+1}
これがβ-1の時分母が0となり計算不能となってしまうのです。
【数理考古学】冪乗算の微積分
Rによる検証例
# Integrate(1→2)(x^β)dx
f0<-function(x)(2^(x+1))/(x+1)-1/(x+1)
f0(-1)
# 確かに計算不能となる。
> f0(-1)
[1] NaN
# 近似値(-1<a)
f0(-1.1)
[1] 0.6696701
> f0(-1.01)
[1] 0.6907505
> f0(-1.001)
[1] 0.692907
> f0(-1.0001)
[1] 0.6931232
> f0(-1.00001)
[1] 0.6931448
> f0(-1.000001)
[1] 0.6931469
> f0(-1.0000001)
[1] 0.6931472
> f0(-1.00000001)
[1] 0.6931472
# 近似値(a<-1)
> f0(-0.9)
[1] 0.7177346
> f0(-0.99)
[1] 0.695555
> f0(-0.999)
[1] 0.6933875
> f0(-0.9999)
[1] 0.6931712
> f0(-0.99999)
[1] 0.6931496
> f0(-0.999999)
[1] 0.6931474
> f0(-0.9999999)
[1] 0.6931472
> f0(-0.99999999)
[1] 0.6931472
# ちなみに正解はlog(2)=0.6931472となる。
> log(2)
[1] 0.6931472
反比例関数y=1/xのグラフでいうと以下の領域ですね。
f0<-function(x){1/x}
plot(f0,xlim=c(0,3),ylim=c(0,3),main="Inverse Proportional Formula")
# 該当箇所の塗り潰し
sqx<-seq(1,2,length=11)
sqy<-f0(sqx)
polygon(
c(1,sqx,2), #x
c(0,sqy,0), #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
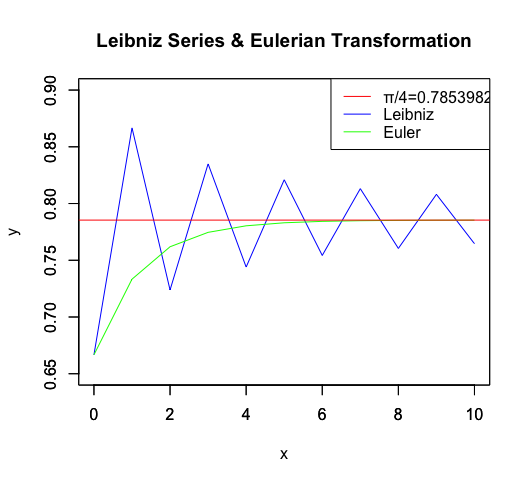
ここで歴史的にはArctangentの収束先π/4を高速で計算したオイラー変換((Eulerien Transformation))の出番となります。「本当に一人? ブルバキみたいな集団ペンネームじゃなくて?」と思うほど、オイラーの出番多過ぎ問題…
【数理考古学】オイラーの公式を導出したマクローリン級数の限界?
cx<-0:10
cy1<-c(0.6666667,0.8666667,0.7238095,0.8349206,0.7440115,0.8209346,0.754268,0.8130915,0.7604599,0.808079,0.7646007)
cy2<-c(0.6666667,0.7333333,0.7619048,0.7746032,0.7803752,0.7830392,0.7842824,0.7848674,0.7851445,0.7852765,0.7853396)
plot(cx,cy1,xlim=c(0,10),ylim=c(0.65,0.9),type="l",col=rgb(0,0,1),main="Leibniz Series & Eulerian Transformation", xlab="x", ylab="y")
par(new=T)#上書き指定
plot(cx,cy2,xlim=c(0,10),ylim=c(0.65,0.9),type="l",col=rgb(0,1,0),main="", xlab="", ylab="")
abline(h=pi/4,col=rgb(1,0,0))
legend("topright", legend=c("π/4=0.7853982","Leibniz","Euler"),lty=c(1,1,1),col=c(rgb(1,0,0),rgb(0,0,1),rgb(0,1,0)))
そして考え方のパラダイムシフトが起こります。任意の(すべての)正の実数はα×2^n(1≦α<2;nは整数)の形に表せるので,log(α×2^n)=log(α)+n×log(2)と示せるのですが…・(ただしここにlog(3,base=2)が混ざり込む)。
Rによる検証例
> 2^0
[1] 1
> 2^1
[1] 2
> 2^0+2^1
[1] 3
# ところで
> 2^1.5849625
[1] 3
> log(3)/log(2)
[1] 1.584963
> log(3,base=2)
[1] 1.584963
# 2^2
> 2^2
[1] 4
> 2^2+2^0
[1] 5
> 2^2+2^1
[1] 6
> 2^2+2^log(3,base=2)
[1] 7
# 2^3
> 2^3
[1] 8
一覧表(8まで)
| Values | Explessions | |
|---|---|---|
| 1 | 1 | 2^0 |
| 2 | 2 | 2^1 |
| 3 | 3 | 2^0+2^1 / 2^log(3,base=2) |
| 4 | 4 | 2^2 |
| 5 | 5 | 2^2+2^0 |
| 6 | 6 | 2^2+2^1 |
| 7 | 7 | 2^2+2^log(3,base=2) |
| 8 | 8 | 2^3 |
target_values<-c("1","2","3","4","5","6","7","8")
target_explession<-c("2^0","2^1","2^0+2^1 / 2^log(3,base=2)","2^2","2^2+2^0","2^2+2^1","2^2+2^log(3,base=2)","2^3")
Regula_falsi04<-data.frame(Values=target_values,Explessions=target_explession)
library(xtable)
print(xtable(Regula_falsi04), type = "html")
つまりlog(2)の値さえ求めておけば,ここで示した近似式を用いて任意の正の実数xの自然対数log(x)の値を計算出来る事になる訳です。こうしてネイピア族も無事整数族と並び立つ形で「実数列そのものへの拡張」を果たす事になったのでした。
対数関数のTylor展開
【無限遠点を巡る数理】等差数列と等比数列②基底関数概念の導入
Rによる検証例
# オイラー変換に従ったLog(2)の計算
> 2/3+2/3*(1/3)^3+2/5*(1/3)^5+2/7*(1/3)^7
[1] 0.6931348
> log(2)
[1] 0.6931472
# log(2)に基づく計算
# log(1)
> log(1)
[1] 0
> log(2)+log(1/2)
[1] 0
# log(3)
> log(3)
[1] 1.098612
> exp(log(3)-log(2))
[1] 1.5
> log(1.5)+log(2)
[1] 1.098612
# log(4)
> log(4)
[1] 1.386294
> log(2)*2
[1] 1.386294
> log(2^2)
[1] 1.386294
# log(5)
> log(5)
[1] 1.609438
> exp(log(5)-log(2^2))
[1] 1.25
>log(1.25)+log(2^2)
[1] 1.609438
# log(6)
> log(6)
[1] 1.791759
> exp(log(6)-log(2^2))
[1] 1.5
> log(1.5)+log(2^2)
[1] 1.791759
# log(7)
> log(7)
[1] 1.94591
> exp(log(7)-log(2^2))
[1] 1.75
> log(1.75)+log(2^2)
[1] 1.94591
# log(8)
> log(8)
[1] 2.079442
> log(2)*3
[1] 2.079442
> log(2^3)
[1] 2.079442
一覧表(8まで)
| Numbers | Explessions | Values | |
|---|---|---|---|
| 1 | log(1) | log(2^1)+log(1/2) | 0 |
| 2 | log(2) | log(2^1) | 0.6931472 |
| 3 | log(3) | log(1.5)+log(2^1) | 1.098612 |
| 4 | log(4) | log(2^2) | 1.386294 |
| 5 | log(5) | log(1.25)+log(2^2) | 1.609438 |
| 6 | log(6) | log(1.5)+log(2^2) | 1.791759 |
| 7 | log(7) | log(1.75)+log(2^2) | 1.94591 |
| 8 | log(8) | log(2^3) | 2.079442 |
target_number<-c("log(1)","log(2)","log(3)","log(4)","log(5)","log(6)","log(7)","log(8)")
target_explession<-c("log(2^1)+log(1/2)","log(2^1)","log(3/2)+log(2^1)","log(2^2)","log(5/4)+log(2^2)","log(3/2)+log(2^2)","log(7/4)+log(2^2)","log(2^3)")
target_values<-c("0","0.6931472","1.098612","1.386294","1.609438","1.791759","1.94591","2.079442")
Regula_falsi04<-data.frame(Numbers=target_number,Explessions=target_explession,Values=target_values)
library(xtable)
print(xtable(Regula_falsi04), type = "html")
何故1と-1は特別なのか。
以下の投稿ではあたかも以下を自明の場合の様に扱ってしまいました。
-1=i^2=(0±1i)^2
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
せっかく等比数列の話が出たので少し掘り下げてみましょう。まず公比=1の時は1^x同様、ただの動かない点に過ぎません。
0<公比<1の時
純粋な1次元展開により0へ向けて収束します。
# 振動関数(Mathematical Oscillation Function)
# 公比D=0.8
MOF01<-function(index){
z0<-complex(real=0.8,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
text(1,0,"1",cex=2,col=rgb(0,0,1))
text(0,0,"0",cex=2,col=rgb(0,0,1))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=c(200,200,200))
abline(v=0, col=c(200,200,200))
}
# アニメーション動作設定
Time_Code<-seq(0,8,length=30)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF36.gif")
公比>1の時
純粋な1次元展開により無限大に向けて発散します。
# 振動関数(Mathematical Oscillation Function)
# 公比D=1.2
MOF01<-function(index){
z0<-complex(real=1.2,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
text(1,0,"1",cex=2,col=rgb(0,0,1))
text(0,0,"0",cex=2,col=rgb(0,0,1))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=c(200,200,200))
abline(v=0, col=c(200,200,200))
}
# アニメーション動作設定
Time_Code<-seq(0,8,length=30)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF37.gif")
公比=-1の時
X軸上から見ると-1と1の間を無限に往復し続ける様に見えます。
# 振動関数(Mathematical Oscillation Function)
# 公比D=-1
# -1^xにi^2=-1を代入
# (0+1i)^2^x=(0+1i)^2x
MOF01<-function(index){
z0<-complex(real=0,imaginary=1)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}
# アニメーション動作設定
Time_Code<-c(seq(-1,1,length=15),rev(seq(-1,1,length=15)))
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF21.gif")
# 振動関数(Mathematical Oscillation Function)
# 公比D=-1
# -1^xにi^2=-1を代入
# (0+1i)^2^x=(0+1i)^2x
MOF01<-function(index){
z0<-complex(real=0,imaginary=-1)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}
# アニメーション動作設定
Time_Code<-c(seq(-1,1,length=15),rev(seq(-1,1,length=15)))
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF22.gif")
0>公比>-1の時
どんどん振幅の幅が狭まっていきます。
# 振動関数(Mathematical Oscillation Function)
# 公比D=-0.8
MOF01<-function(index){
z0<-complex(real=-0.8,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}
# アニメーション動作設定
Time_Code<-seq(0,8,length=90)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF24.gif")
公比<-1の時
どんどん振幅の幅が広がっていきます。
# 振動関数(Mathematical Oscillation Function)
# 公比D=-1.2
MOF01<-function(index){
z0<-complex(real=-1.2,imaginary=0)
f0<-function(x)z0^(2*x)
c0<-f0(index)
cx<-Re(c0)
cy<-Im(c0)
plot(cx,cy,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="Mathematical Oscillation Function",xlab="X axis",ylab="Y axis")
text(cx,cy,"X",cex=2,col=rgb(0,1,0))
segments(0,0,cx,cy,col=rgb(0,1,0))
abline(h=0, col=rgb(1,0,0))
abline(v=0, col=rgb(1,0,0))
}
# アニメーション動作設定
Time_Code<-seq(0,8,length=90)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
MOF01(i)
}
}, interval = 0.1, movie.name = "MOF25.gif")
そう、一点で留まってるのは1のみ、ちゃんと周回軌道を描くのは-1のみなんですね。
Rによる確認例
> (0-1i)*(0+1i)
[1] 1+0i
> (0+1i)*(0-1i)
[1] 1+0i
> (0-1i)*(0-1i)
[1] -1+0i
> (0+1i)*(0+1i)
[1] -1+0i
ここ数年取り組んできた「数についての考え方の総まとめ」その2。そんな感じで以下続報…