【Python演算処理】単位球面(Unit Shere)を巡る数理②そして単位トーラス(Unit Torus)へ

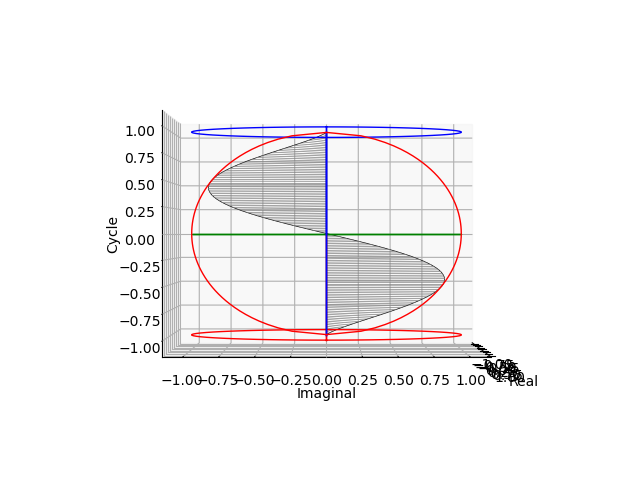
考えてみれば、以下のアニメーションをちゃんと目で追える様になれば二次元/三次元座標系の三角関数における$\cos(θ)$と$\sin(θ)$の働きを概ね理解出来たといえそうです。
【Python演算処理】単位球面を巡る数理①とりあえず描画してみる。

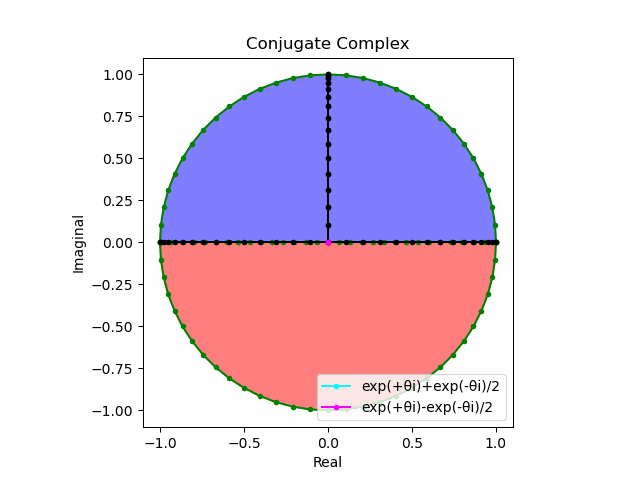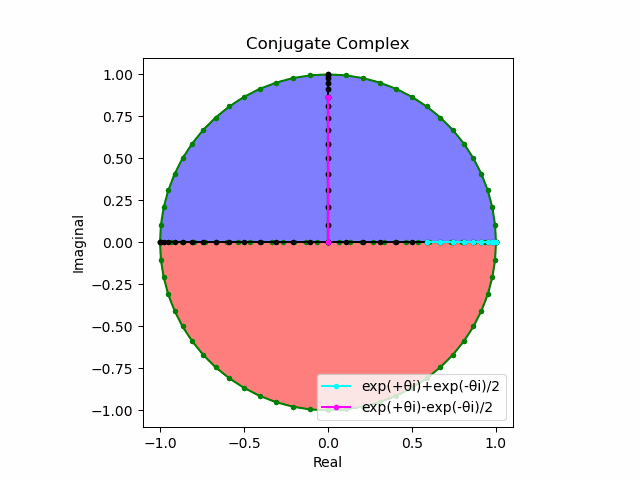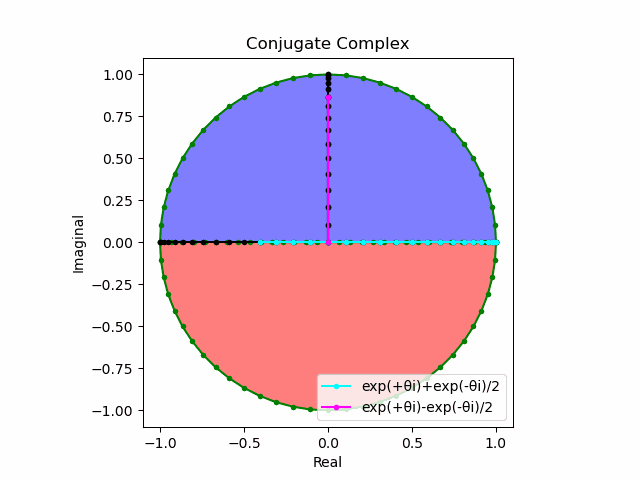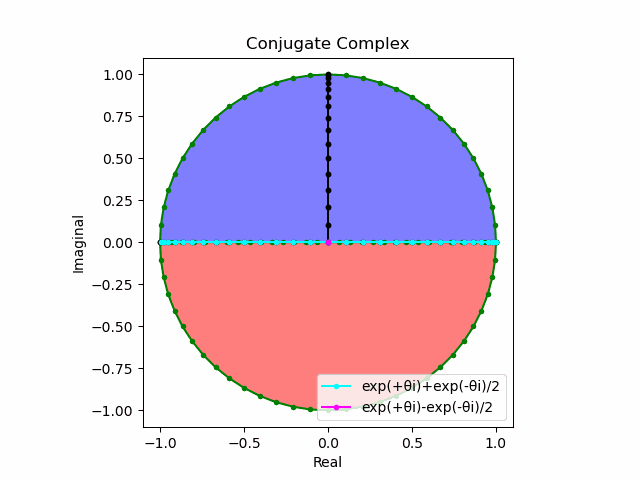
\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}\\
\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}

最後のアニメーションを目で追う際には、以下の円筒アニメーションが参考となるでしょう。
【Python演算処理】単位円筒を巡る数理

つまりはこういう事です。


$\sin(θ)\cos(θ)$波の検出

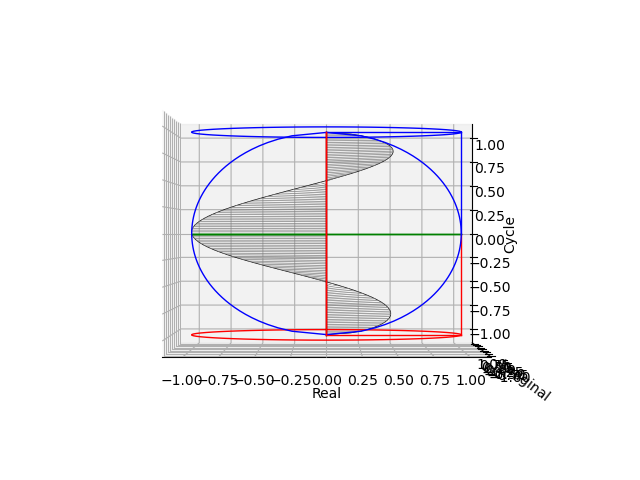
• 0/2πラジアンの時0
• ±$\frac{π}{2}$ラジアンの時$\frac{1}{2}$
• πラジアンの時-1

$\sin(θ)\sin(θ)$波の検出

• 0/2π/±$\frac{π}{2}$ラジアンの時0
• 半径±$\frac{1}{2}$の時に頂点

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円球データ作成
def src(x):
    return m.sqrt(1-x**2)
c0=num.linspace(0,m.pi*2,121,endpoint = True)
z0=num.linspace(-1,1,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm])*src(z0[nm]),m.sin(c0[nm])*src(z0[nm])))
s1=num.array(s0)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    #スポーク描画
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,-1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #球面描画
    ax.plot(MiBx,MiHy,MiHz,color="blue",lw=1)
    ax.plot(-MiBx,MiHy,MiHz,color="blue",lw=1)
    ax.plot(MiHy,MiBx,MiHz,color="red",lw=1)
    ax.plot(MiHy,-MiBx,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=10, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output552.gif", writer="pillow")

おや、垂直方面から眺めると思わぬ図形が…これは「尻の割れ目」?
【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！

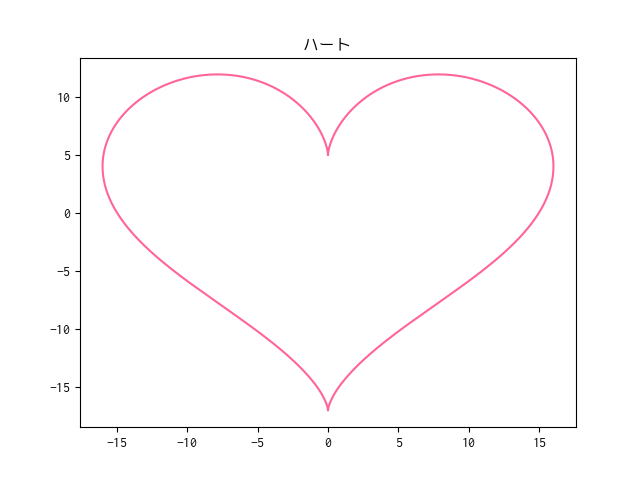
さらに調整を加えるとハート型になる様です。
Python でハートを描く

そして周期=1の場合。水平方向と垂直方向のアスペクト比2:1なので潰れて饅頭の様な形に。


sin(θ)cos(θ)波の検出

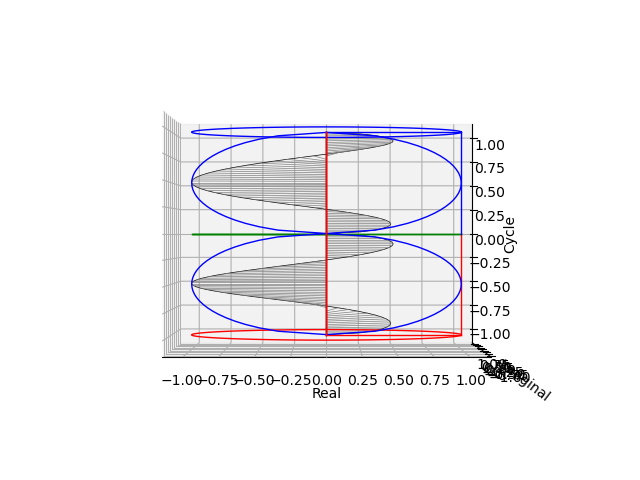
sin(θ)sin(θ)波の検出

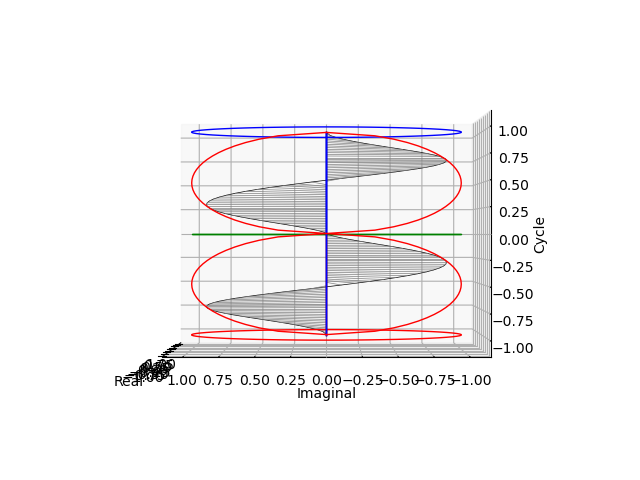
もちろん上面図(XY面)からの見え方は変わらない。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円球データ作成
def src(x):
    return m.sqrt(1-x**2)
c1=num.linspace(0,m.pi*2,60,endpoint = False)
c2=num.linspace(0,m.pi*2,61,endpoint = True)
c0=num.concatenate([c1, c2])
z0=num.linspace(-1,1,121,endpoint = True)
zc1=num.linspace(-1,1,60,endpoint = False)
zc2=num.linspace(-1,1,61,endpoint = True)
zc=num.concatenate([zc1,zc2])
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm])*src(zc[nm]),m.sin(c0[nm])*src(zc[nm])))
s1=num.array(s0)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiBH1=num.linspace(-1,1,30,endpoint = False)
MiBH2=num.linspace(-1,1,31,endpoint = True)
MiBH=num.concatenate([MiBH1,MiBH2])
MiBx=num.sqrt(1-MiBH**2)
MiHy=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    #スポーク描画
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #球面描画
    ax.plot(MiBx,MiHy,MiHz,color="blue",lw=1)
    ax.plot(-MiBx,MiHy,MiHz,color="blue",lw=1)
    ax.plot(MiHy,MiBx,MiHz,color="red",lw=1)
    ax.plot(MiHy,-MiBx,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=10, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output560.gif", writer="pillow")

極座標系(Polar Coordinate System)表示の二次元版/3次元版

ここで改めて極座標系(Polar Coordinate System)表示の二次元版/三次元版について振り返ってみたいと思います。

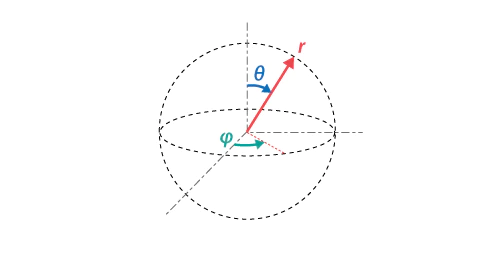
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換

• 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
• $φ=-(\arctan^2(x,y)-\frac{π}{2})$
• $x=r×\cos(φ)$
• $y=r×\sin(φ)$

三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換

• 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
• $φ=-(\arctan^2(x,y)-\frac{π}{2})$
• $θ=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
• $x=r×\sin(θ)\cos(φ)$
• $y=r×\sin(θ)\sin(φ)$
• $z=r×\cos(θ)$

また、球の体積を求める三重積分は以下の様に規定されています。
EMANの物理学>物理数学>線積分
EMANの物理学>物理数学>面積分と体積分
EMANの物理学>物理数学>ヤコビアン

\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\
=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix}
\frac{∂x}{∂r} & \frac{∂x}{∂θ}  & \frac{∂x}{∂φ}\\
\frac{∂y}{∂r} & \frac{∂y}{∂θ}  & \frac{∂y}{∂φ}\\
\frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ}
\end{vmatrix} drdθdφ

積分範囲の積み重ね方に注目すると以下となってます。
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」？

• まずは角度$φ=0→2π$の範囲で積分して円周$2πr$に到達。
• さらに角度$θ=0→π$の範囲で積分を重ね球の表面積$4πr^2$に到達。
• さらに半径$r=0→1$の範囲で積分を重ね球の体積$\frac{4}{3}πr^3$に到達。

こうした計算では「θがφの半分になる事」事が自明の場合(Trival Case)として扱われていますが、実はこの辺りが曲者だったりするのです。

そして単位トーラス(Unit Torus)へ

結論から先に述べると、どうやら上掲の円/球面座標系はトーラス座標系(Torus Coordinates System)のごく一部を援用しているに過ぎない様なのです。大半径(Major Radius)Rと小半径(Minor Radius)の組み合わせで表現されるそれとデカルト座標系の関係は、一般に媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表されます。

• x=$R×\cos(t)+r×\cos(p)\cos(t)$
• y=$R×cos(t)+r×\cos(p)\sin(t)$
• z=$r×\sin(p)$

上掲の円/球面座標系との関係は以下。

• 大半径R=0,小半径r=1の時、単位球面(Unit Sphere)を二重に描く。従って経緯度法(経度-180度→+180度に対して緯度-90度→+90度)や3次元極座標系(水平角φ=-π→+πに対して垂直角θ=0→π)は適用範囲を半分に減らしてなお単位球面(Unit Sphere)上の全座標を示せる訳である。
• 逆に大半径R=1,小半径r=0の時、Z=0となってただの単位円(Unit Circle)となる。大半径Rと小半径rの比が1:1の場合(外径が半径1の単位円と一致するのは大半径R=小半径r=$\frac{1}{2}$の時で、大半径R=小半径r=1の時の外径は2となる）からこの極限状態に向かう展開は「半径1の単位円に内接する正N角形とそのさらなる内接円の推移($N=\infty$に近づくほど、その正N角形の辺長計は円周長2πに限りなく近づく)」数理そのものである。
  【初心者向け】挟み撃ち定理による円周率πの近似
  

そう、両者が本来連続しているという事は隠された中間状態が存在するのです。特に大半径Rと小半径rの比が1:1の場合が重要なので、これを単位トーラス(Unit Torus)と呼び分けたいと思います。

Rの場合

トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ

pythonの場合

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #   ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ##ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ##ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,2],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="blue",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="red",lw=1)
    ax.plot([0,2],[0,0],[1,1],color="black",lw=1)
    ax.plot([2,2],[0,0],[-1,1],color="black",lw=1)
    #小半径描画
    ax.plot(MiPx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiMx,MiHy,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output531.gif", writer="pillow")

今度は「ヘモグロビン」が現れた？
健康診断で、ヘモグロビン値が高い・低いと言われたら？

• 大半径R=小半径r=1(外径2)の時と大半径R=小半径r=$\frac{1}{2}$(外径1)の時のどちらを単位に選ぶかは状況による。
• その状況はまさに円筒座標系において周回ピッチを1周と置くか(分枝切断点1)、半周と置くか(分枝切断点2) に対応する。
  【Python演算処理】単位円筒を巡る数理
  1周と置く場合(Γ関数との関連が発生)
  
  
  半周と置く場合(偶奇性との関連が発生)
  
  

そう、どうやらある意味、かかる単位トーラス概念の登場こそが偶奇(Patity)の概念の大源流となる様なのです。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

この数理がトーラス座標系における以下の表示に対応する訳です。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #   ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ##ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ##ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,2],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="blue",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="red",lw=1)
    ax.plot([0,2],[0,0],[1,1],color="black",lw=1)
    ax.plot([2,2],[0,0],[-1,1],color="black",lw=1)
    #小半径描画
    ax.plot(MiPx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiMx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiBx,MiHy,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output540.gif", writer="pillow")

さらに小半径をアニメーションさせてみましょう。とりあえず極座標系rφθにおいてφ=θと置いて外回し(時計回り)。こうして図示してみると経度(±90度)が緯度(±180度)の半分、三次元曲座標系rφθにおいて垂直角θ(π)が水平角φ(2π)の半分となるのは「復路」を省いているからだという事が一目瞭然で分かります。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh=num.concatenate([MiAh1, MiAh2[::-1]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv=num.concatenate([MiAv1, MiAv2])

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #   ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ##ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ##ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,2],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="blue",lw=1)
    ax.plot([1,2],[0,0],[0,0],color="black",lw=1)
    ax.plot([1,1],[0,0],[-1,1],color="black",lw=1)    
    ax.plot([1,MiAv[n]],[0,0],[0,MiAh[n]],color="red",lw=1)
    ax.plot([0,2],[0,0],[1,1],color="black",lw=1)
    ax.plot([2,2],[0,0],[-1,1],color="black",lw=1)
    #小半径描画
    ax.plot(MiPx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiMx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiBx,MiHy,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output574.gif", writer="pillow")

実軸(Real Axis)に絡めると反時計回りが正解に思えます。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #   ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ##ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ##ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,2],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="blue",lw=1)
    ax.plot([1,2],[0,0],[0,0],color="green",lw=1)
    ax.plot([1,1],[0,0],[-1,1],color="black",lw=1)    
    ax.plot([1,MiAv[n]],[0,0],[0,MiAh[n]],color="red",lw=1)
    ax.plot([0,2],[0,0],[1,1],color="black",lw=1)
    ax.plot([2,2],[0,0],[-1,1],color="black",lw=1)
    #小半径描画
    ax.plot(MiPx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiMx,MiHy,MiHz,color="red",lw=1)
    ax.plot(MiBx,MiHy,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output590.gif", writer="pillow")

そしていよいよ、世界全体を回すインチキ回転からの脱却…cmath.rect()関数を導入するとあっけないほど簡単に移行が完了してしまいました。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #アニメーション演算
    Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
    MiAvD0=[]
    for nm in range(len(MiAvC)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0)  
    #中心円
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)  
    #外縁線
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)  
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #   ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ##ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ##ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="green",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="red",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    #小半径描画
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output588.gif", writer="pillow")

そしてかかる半径1の単位円/球(偶数系)と大半径=小半径1の単位トーラス(奇数系)の関係を連鎖させ、半径が整数倍の同心円/同心球面座標系(スカラーの世界=角度の概念が存在しない極座標系)に発展させるのは、自明の場合(Trival Case)の範疇に入りそうです。それとも何か厳密な証明が必要?
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

0.5次元と1次元の狭間

【数理考古学】とある実数列の規定例③オイラーの等式が意味するもの？

0.5次元の到達地点は2次元/3次元の極座標系の検知である。


自明の場合(Trival Case)として次の段階において獲得済の半径と垂直に交わる新たな半径を伸ばしたのがトーラス座標系といえよう。しかし実際の次の着地点となる1次元は数直線(Number Line)のみを実軸(Real Axis)とする円筒座標系なのである。

この矛盾を解決するにはトーラス座標系を分枝切断して「アイロンを当てた様に真っ直ぐに伸ばした上で」改めて連続性を確保しないといけません。なら、どうやって？　それについては以下続報…