【Python演算処理】単位球面(Unit Shere)を巡る数理①とりあえず描画してみる。

• (2021年4月09日)投稿。
• (2021年4月12日)回転方向を反時計回りで統一。

昔から以下にモヤモヤしたものを感じてきました。
等速円運動についての物理学と数学の立場の違い?

• 物理学において等速円運動は「Y軸に沿って単位時間1辺り単位距離1進む等速直線運動が、直交するX軸沿いに働く向心加速度(Centripetal Acceleration)1の影響を受け続ける結果」と表現され「結果として単位時間辺り$\frac{π}{2}$進む」事への直接言及がない。
• 一方、幾何学上はこの球表面上の運動は角度(回転速度)の問題として処理され、(2π=1周と置く)ラジアン表記の場合、4単位時間で1周するならその移動速度が$\frac{π}{2}$/単位時間毎である事が自明の場合(Trival Case)として示される一方、その運動が元来「軸線に沿って単位時間1辺り単位距離1進もうとする等速直線運動」である事への直接言及がない。

しかも単振動(Simple vibration)、すなわち直径上の等速直線運動と実際の円弧上の動きを対応させる三角関数の定義には、新たに（引数で与えられた数列を対数尺に配置する）指数関数(Exponential Function)と(直線座標系において、それからはみ出す直交座標軸操作を扱う)複素数表現(Complex Expression)が登場してくるのです。

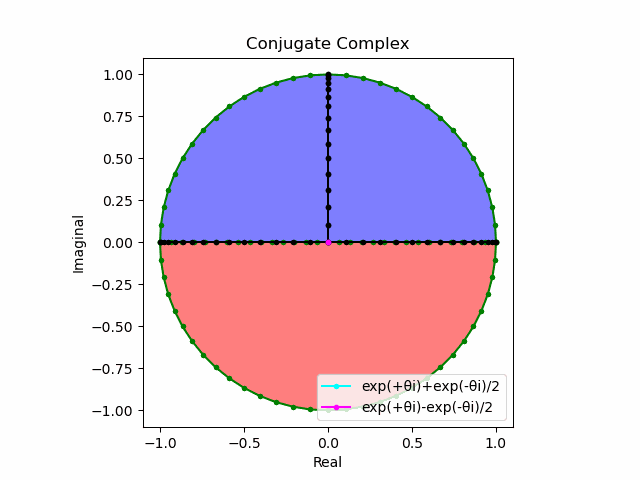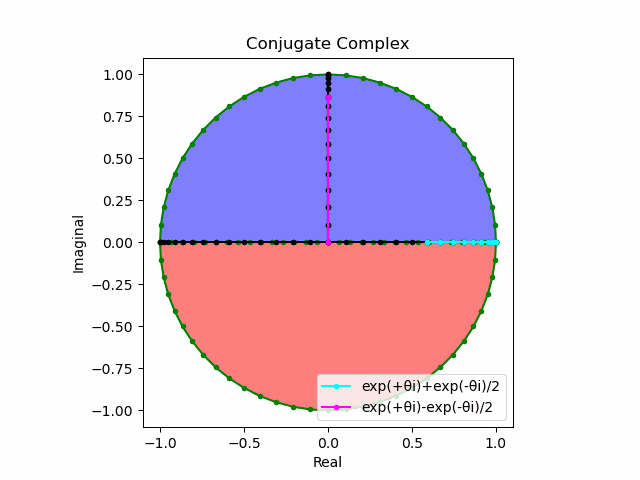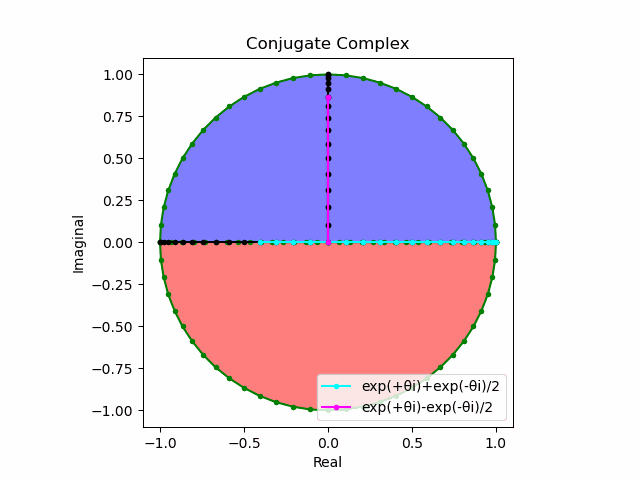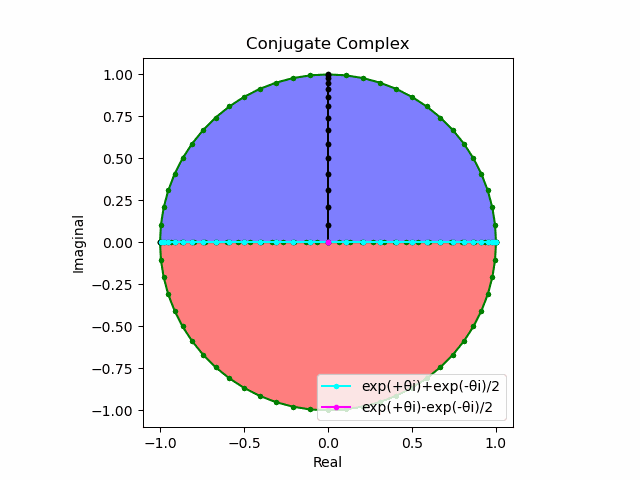
\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}\\
\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}

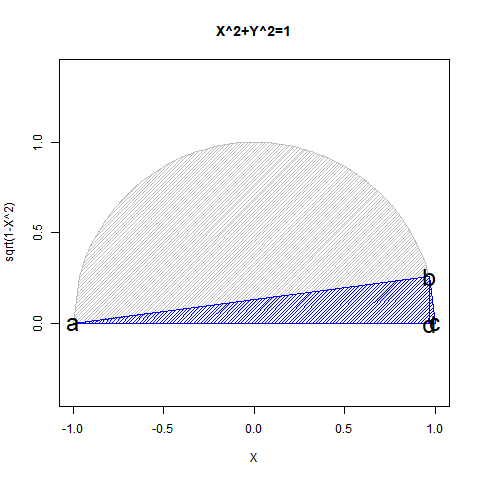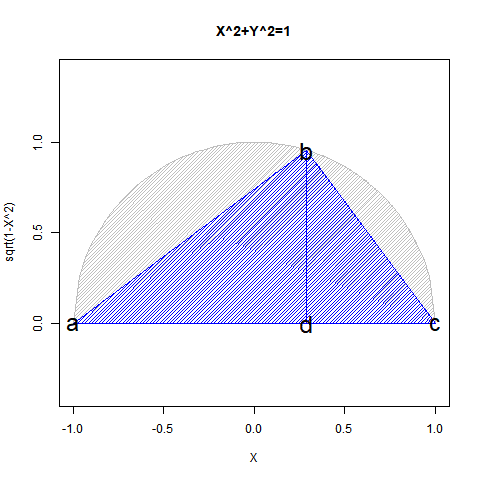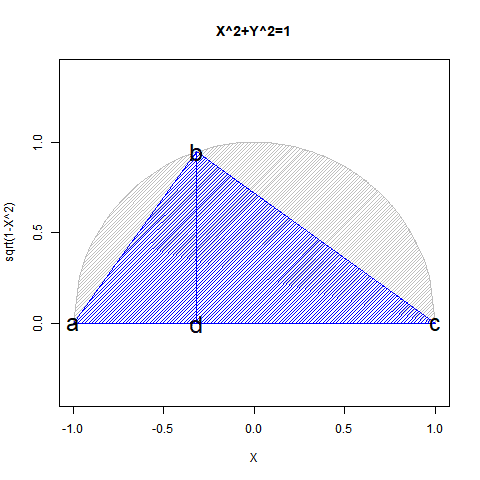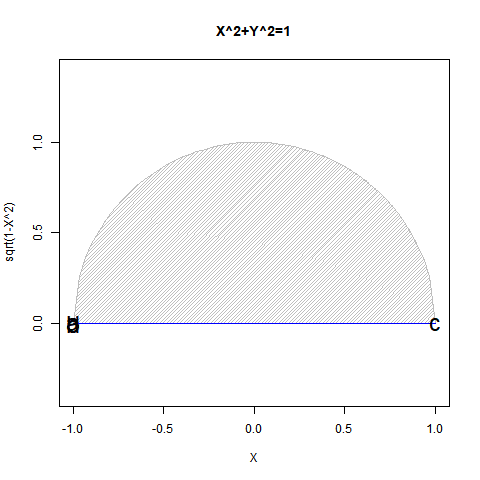
こうした数理とピタゴラスの定理(Pythagorean Theorem)に基づいて単位円を半分だけ描く式$y=\sqrt{1-x^2}$の関係は？　定理系として演算内容が閉じてない様にも見えるんですが、この辺りの事についてみんな、どうやって頭の中で決着を付けてるんでしょうか？
【Rで球面幾何学】「半円しか描けなかった」世界の思い出？

ガウスが発見した1の冪乗根(Root of Unity)$Z^n=1$を巡る数理(ここにも三角関数が現れる)同様、今日なおオイラーの公式(Eulerian Formula)$e^{πi}=(1±\frac{πi}{n})^n=\cos(θ)+\sin(θ)i$が「人類の至宝」ともてはやされる反面で「その内容について深く考えても時間の無駄である」なる諦念が広まっているのにはこういう背景もあるのですね。まぁノイマン博士も「数学に「分かる」はない。「慣れる」があるだけだ」と断言してますし、究極的には実際に数理にそういう側面がある事は否めないのですが…
【初心者向け】挟み撃ち定理による円周率πの近似

一辺の長さがaの正n角形に外接する円の半径**r**

1. $r=\frac{a}{2\tan(\frac{π}{n})}$
2. $a=r(2\tan(\frac{π}{n}))$

一辺の長さがAの正n角形に内接する円の半径**R**

1. $R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
2. $A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$

一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係

1.$r=Rcos(\frac{π}{n})$
2.$R=\frac{r}{cos(\frac{π}{n})}$

外接円を単位円（Unit Circle）としたのが上記アニメーション。

1. 外接円の半径**R**は単位円の定義に従って1
2. これに内接する正多辺形の１辺の長さ**A**は$2\tan(\frac{π}{辺数})cos(\frac{π}{辺数})$
3. 外接円に内接する正多辺形の内接円の半径**r**は$cos(\frac{π}{辺数})$

#単位円筒(Unit Cylinder)から単位球面(Unit Shere)へ
しかしまぁ、背景となる理論が分からないなりに上掲くらいジタバタ出来る様になれば(本当の数学諸学者だった頃の数年前の自分にはそれさえ出来なかった)、自然に出来る事も勝手に増えていくものです。例えば…
【Python演算処理】単位円筒を巡る数理

この円筒表現のZ軸に「曲率」として式$y=\sqrt{1-x^2}$を与えると球表面表現となります。R時代に使っていた以下のアルゴリズムの移植。ついでに上掲の「(XY軸上の)Sin波の動き」のZ軸上の動きも追加してみましたが、なんだか目で追うのが難しい…
【初心者向け】「単位円筒」から「単位球面」へ

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.sqrt(1-cutz**2)
cuty=num.repeat(0,61)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=1)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,cutx[n]],[0,0],[0,cutz[n]],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output510.gif", writer="pillow")

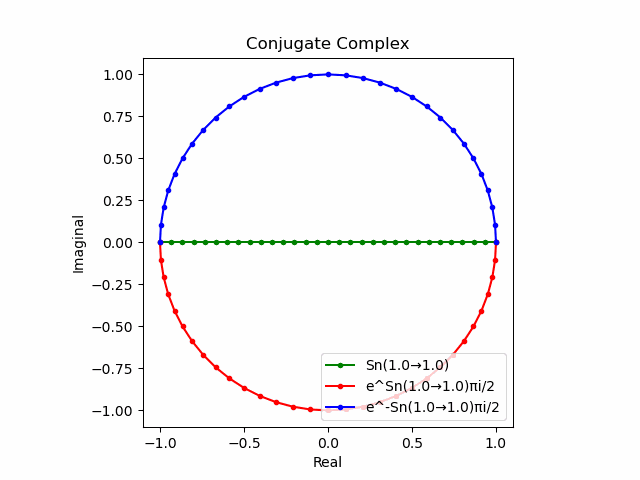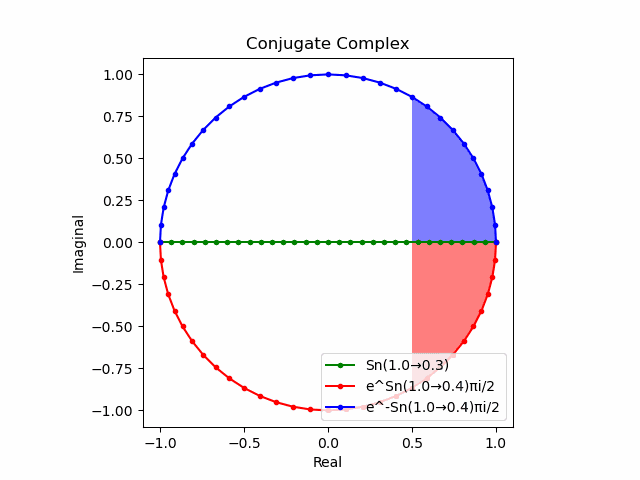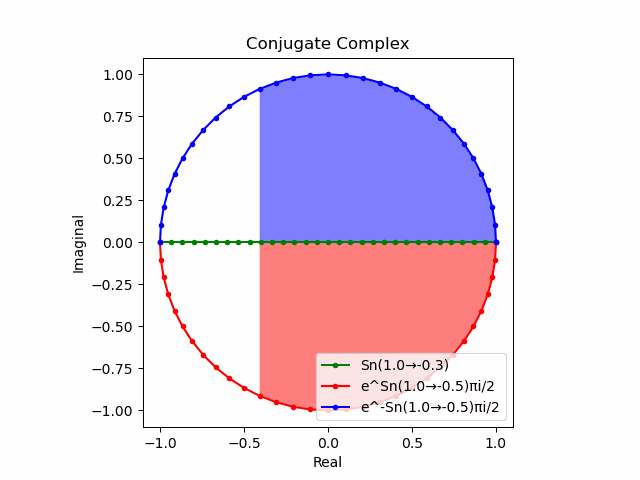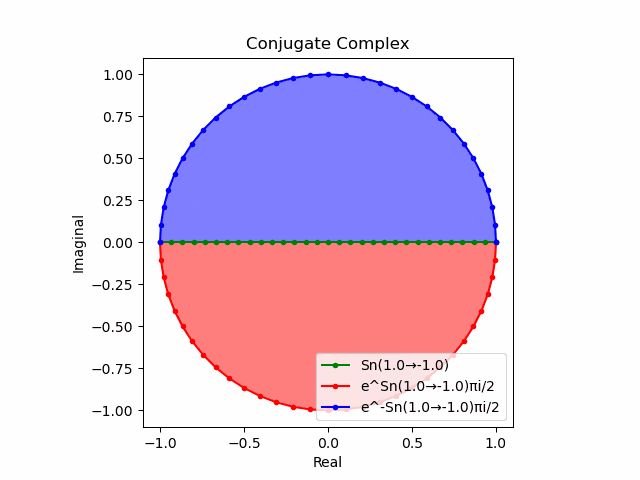
「波形の位相が90度(π/2ラジアン)ズレていく」連鎖を強調すべく、さらに「(Z軸にはみ出した)XY軸上のSin波」と直交する「共役軸」を取ってみます。ここでいう「共役軸」は、球面座標系の特徴に従って(地球儀上における緯度集合の様な)、中心からの距離もZ軸上の座標も同じ集合を構成するのです。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.sqrt(1-cutz**2)
cuty=num.repeat(0,61)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)

#断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    ucutz=num.full(61,cutz[n])
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for nm in range(len(uc)):
        ax.plot([0,uc[nm].real],[0,uc[nm].imag],[0,0],color="olivedrab",lw=1)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="black",lw=1)
    ax.plot([0,cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
    ax.plot([0,cuty[n]],[0,-1*cutx[n]],[0,cutz[n]],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,0],[0,1],[0,0],color="blue",lw=1)
    ax.plot([0,0],[0,-1],[0,0],color="red",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="black",lw=1)
    ax.plot(cuty,cutx,cutz,color="blue",lw=1)
    ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
    #断面円描画
    ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output519.gif", writer="pillow")

かえって目で追い難くなってしまいました。それではさらに表示内容を三次元極座標(r,θ,φ)形式に寄せてみましょう。

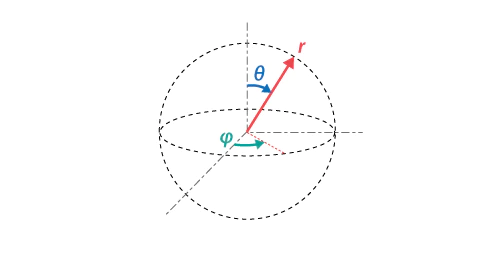
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換

• 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
• $φ=-(\arctan^2(x,y)-\frac{π}{2})$
• $x=r×\cos(φ)$
• $y=r×\sin(φ)$

三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換

• 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
• $φ=-(\arctan^2(x,y)-\frac{π}{2})$
• $θ=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
• $x=r×\sin(θ)\cos(φ)$
• $y=r×\sin(θ)\sin(φ)$
• $z=r×\cos(θ)$

$φ=θ=2π/1周期$なので以下の様に見えます。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.sqrt(1-cutz**2)
cuty=num.repeat(0,61)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)

#断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    ucutz=num.full(61,cutz[n])
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for nm in range(len(uc)):
        ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="black",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="purple",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[cutz[n],cutz[n]],color="purple",lw=1)
    ax.plot([0,cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
    ax.plot([0,cuty[n]],[0,-1*cutx[n]],[0,cutz[n]],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="purple",lw=1)
    ax.plot([0,0],[0,1],[0,0],color="blue",lw=1)
    ax.plot([0,0],[0,-1],[0,0],color="red",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="purple",lw=1)
    ax.plot(cuty,cutx,cutz,color="blue",lw=1)
    ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
    #断面円描画
    ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output521.gif", writer="pillow")

おやおや、どうやら球表面の面積を求める式$4πr^2$や球の体積を求める式$\frac{4}{3}πr^3$を導出する三重積分が以下のプロセスを辿る事とも何か関係がありそうです。

\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\
=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix}
\frac{∂x}{∂r} & \frac{∂x}{∂θ}  & \frac{∂x}{∂φ}\\
\frac{∂y}{∂r} & \frac{∂y}{∂θ}  & \frac{∂y}{∂φ}\\
\frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ}
\end{vmatrix} drdθdφ

積分範囲の積み重ね方に注目すると以下となってます。

• まずは角度$φ=0→2π$の範囲で積分して円周$2πr$に到達。
• さらに角度$θ=0→π$の範囲で積分を重ね球の表面積$4πr^2$に到達。
• さらに半径$r=0→1$の範囲で積分を重ね球の体積$\frac{4}{3}πr^3$に到達。

こちらもやはり「(垂直角)θは(水平角)φの半分」と考える訳ですね。

それにつけても…なんか「球」というよりマカロンとか、ハル・クレメント「重力の使命(Mission of Gravity,1954年)」に登場する超高速回転惑星メスクリンみたいに潰れてますが、みんなこの「matplotlibの球」を我慢して使ってる訳で、そこは妥協するものとします。
マックカフェ、マカロンの人気フレーバーが復活！

惑星メスクリン

こうした展開の鍵となってくるのが「2軸で1つの極座標系を構成する」XY軸と異なり、それと直交して線型独立しているZ軸に対する操作の独立性。例えば「曲率」の設定はロクロで回してる粘土に型を押し付けてるイメージで、式$y=|x|$を与えると円錐が出現します。
【初心者向け】線形関数や絶対値関数

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv1=num.linspace(-1,1,1201,endpoint = True)
#cv1=num.sqrt(1-cv0**2)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.abs(cutz)
cuty=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=1)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=25, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1] 
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output512.gif", writer="pillow")

一方、上掲の球表現で「曲率」設定をそのまま置いてZ軸の尺を均等尺から対数尺に差し替えると「卵形」が現出するのです。
これもR時代に発見した表現。ただし「mathplotlibの球」はマカロン型なので、一見してそれと分からないのが残念至極。カンブリア爆発期における視覚とその情報を処理する脊髄の獲得まで遡る人間の図形/空間把握能力は、こういう部分が案外繊細に出来ているのであった…

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.exp(num.linspace(-1,1,1201,endpoint = True))

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#安易に指数関数を乱用したら極端に重くなったので定数化。
zp1=num.exp(1)
z00=num.exp(0)
zm1=num.exp(-1)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz1=cutz0[::-1]
cutz=num.exp(cutz1)
cutx=num.sqrt(1-cutz1**2)
cuty=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(zm1,61)
uz1=num.repeat(z00,61)
uz2=num.repeat(zp1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[z00,z00],color="olivedrab",lw=1)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[zm1,zp1],color="black",lw=1)
    ax.plot([0,1],[0,0],[zm1,zm1],color="red",lw=1)
    ax.plot([0,1],[0,0],[z00,z00],color="black",lw=1)
    ax.plot([0,cutx[n]],[0,0],[z00,cutz[n]],color="black",lw=1)
    ax.plot([0,1],[0,0],[zp1,zp1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[zm1,z00],color="red",lw=1)
    ax.plot([1,1],[0,0],[z00,zp1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([zm1,zp1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output514.gif", writer="pillow")

こちらも「直交するZ軸上の共役軸」を追加しておきましょう(上面図は球面のそれと同じ)。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.exp(num.linspace(-1,1,1201,endpoint = True))

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#安易に指数関数を乱用したら極端に重くなったので定数化。
zp1=num.exp(1)
z00=num.exp(0)
zm1=num.exp(-1)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz1=cutz0[::-1]
cutz=num.exp(cutz1)
cutx=num.sqrt(1-cutz1**2)
cuty=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(zm1,61)
uz1=num.repeat(z00,61)
uz2=num.repeat(zp1,61)

#断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    ucutz=num.full(61,cutz[n])
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for nm in range(len(uc)):
        ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="black",lw=1)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[zm1,zp1],color="black",lw=1)
    ax.plot([0,1],[0,0],[zm1,zm1],color="red",lw=1)
    ax.plot([0,1],[0,0],[z00,z00],color="purple",lw=1)
    ax.plot([0,0],[0,1],[z00,z00],color="blue",lw=1)
    ax.plot([0,0],[0,-1],[z00,z00],color="red",lw=1)
    ax.plot([0,cutx[n]],[0,0],[z00,cutz[n]],color="purple",lw=1)
    ax.plot([0,cutx[n]],[0,0],[cutz[n],cutz[n]],color="purple",lw=1)
    ax.plot([0,cuty[n]],[0,cutx[n]],[z00,cutz[n]],color="blue",lw=1)
    ax.plot([0,cuty[n]],[0,-1*cutx[n]],[z00,cutz[n]],color="red",lw=1)
    ax.plot([0,1],[0,0],[zp1,zp1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[zm1,z00],color="red",lw=1)
    ax.plot([1,1],[0,0],[z00,zp1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="purple",lw=1)
    ax.plot(cuty,cutx,cutz,color="blue",lw=1)
    ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
    #断面円描画
    ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([zm1,zp1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output528.gif", writer="pillow")

それにつけても本当に…「卵形」というより、むしろ水木しげる画伯の描いた妖怪タンコロリンじゃないですか!!　このまま放置しておいたら、きっとそのうち反乱起こりますよ…
妖怪タンコロリン-Pixiv百科事典

それはそれとして、物理学も等速円運動を向心加速度(Centripetal Acceleration)で説明するし、鶏卵があの形なのも重力に関係する説があるし(その説においては、子宮内における黄身だけの状態だと球形なのが、卵殻の形成が始まって黄身が白身に浮かんだ状態で産道を通過する過程で重力の影響を受けてあの形となると考える)、指数関数と重力を結びつける逸話には本当に事欠きません。そういえばR時代にはベルカーブ曲線$e^{-x^2}$に由来する誤差関数(ERF=Error Function)を円尺に射影するとブラックホールの景観(重力レンズ効果によって球面の裏側まで映り込んだ状態)になるという発見もあったのです。
【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。

ただし見ての通り(カンブリア爆発期における視覚とその情報を処理する脊髄の獲得まで遡る)人間の図形/空間把握能力は、かかる「裏面」をあっけなく「誤差」として切り捨てて視野外に追いやってしまいます。そもそも誤差関数の役割は、そうやって「誤差として切り捨てる範囲」に計算上の指針を与える事なんですね(実際にどの範囲までを切り捨てるかは人間が決める)。そう考えると当然といえば当然の結果とも？

そんな感じで以下続報…