関数による演算結果の集合(Function Result Set)について考える場合、その最も単純な関数集合(Function Set)の例は線形関数(Linear Function)y=±xや絶対値関数(Absolute Value Function)y=±abs(x)/x=±abs(y)となります。
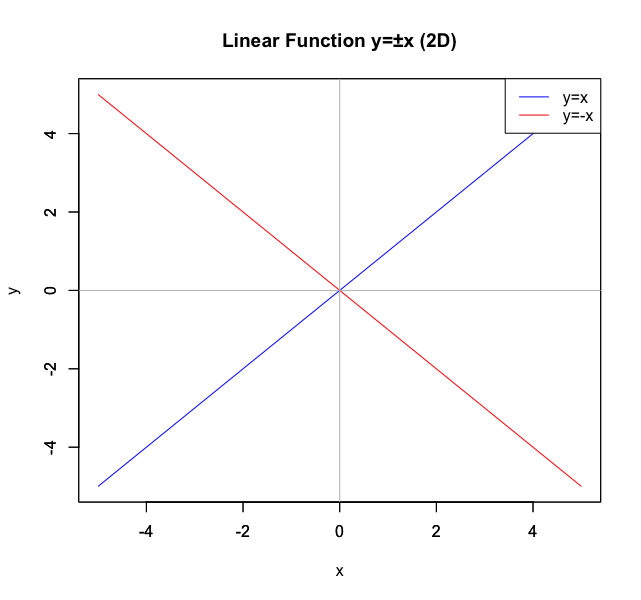
線形関数(Linear Function)y=±x
最もオーソドックスな二次元(2D)上での見え方は平方対角線(Square Diagonal)めいた以下でしょう。y=xは第1象限(1st Orthant,x=y=正数(Positive Number))と第3象限(3rd Orthant,x=y=負数(Negative Number))に、y=-x(-x=y)は第2象限(2nd Orthant,x=正数/y=負数)と第4象限(4th Orthant,x=負数/y=正数)に展開。
正の数と負の数 - Wikipedia
# コンピューター演算は無限(Infinity)の概念を
# 直接は扱えないので状況に応じて適切な
# 変域(Domain)を定める必要がある。
# ここでは-5から5までの整数を設定
cx<-seq(-5,5,length=11)
cy_plus<-cx
cy_minus<--cx
plot(cx,cy_plus,type="l",xlim=c(-5,5),ylim=c(-5,5),main="Linear Function y=±x (2D)",xlab="x",ylab="y", col=rgb(0,0,1))
par(new=T)
plot(cx,cy_minus,type="l",xlim=c(-5,5),ylim=c(-5,5),main="",xlab="",ylab="", col=rgb(1,0,0))
# 基準線はx=0,y=0の2本。
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
# 凡例を書き添える 。
legend("topright", legend=c("y=x","y=-x"), lty =c(1,1),col=c(rgb(0,0,1),rgb(1,0,0)))
-
関数表現(Function Expression)には複素数表現(Complex Expression)同様、x→-x/-x→xといった向きの情報が完全に欠落している。あくまで「特定の増え方をする関数は必ず同じ減り方をする」事が前提となっているのである。
【初心者向け】複素共役のアニメーション表示について。


座標系を三次元(3D=Three Dimension)に拡張すると立方対角線(Cubic diagonal)が2本追加となって象限も8分割されます。

# y=xは何次元に拡張しても1本線のままだが、
# y=-xでは符号を逆転するのがY軸かZ軸かという
# 選択肢が現れる。
library(rgl)
cx<-seq(-5,5,length=11)
cy_plus<-cx
cy_minus<--cx
plot3d(cx,cy_plus,cy_plus,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,cy_minus,cy_minus,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_plus,cy_minus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_minus,cy_minus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(-5,5),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test14")
それぞれの意味が以下となります。独立変数Xに対応して2次元だと{Y},{-Y}、3次元だと{Y,Z},{-Y,-Z},{-Y,Z},{Y,-Z}が対応するイメージ?
- X=Y=Z…既存のX=Y関数の自然な拡張。この関数だけは何次元に拡張しようとこんな感じ。おそらく幾何学的構造における対蹠概念に対応する。そして四元数(Quaternion)a+bi+cj+dkのa。
- X=-Y=-Z…既存のX=-Y関数の自然な拡張。XとZの傾きが連動。
- X=-Y=Z…新規追加分。XとZの傾きが連動。
- -X=-Y=Z(X=Y=-Z)…新規追加分。XとYの傾きが連動。
これが事実上の象限表現(Orthant Expression)となる様です?
相関方向分析法
第一象限、第二象限などの意味と覚え方
三次元座標空間においては、象限の(有名な)定義は無いようです。
数学における座標平面の文脈では、第一象限は必ず右上です。しかし、他の分野では、4つに分けた領域の左上部分を第一象限(第一の領域)と呼ぶ人もたまにいます。人間は、文章などを左上から見ることが多いため、左上部分を「第一」と認識するのも、ある意味では妥当かもしれません。
Cos(θ)+Sin(θ)i(反時計回り)派とSin(θ)+Cos(θ)i(時計回り)派が鋭く対峙する世界?
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ


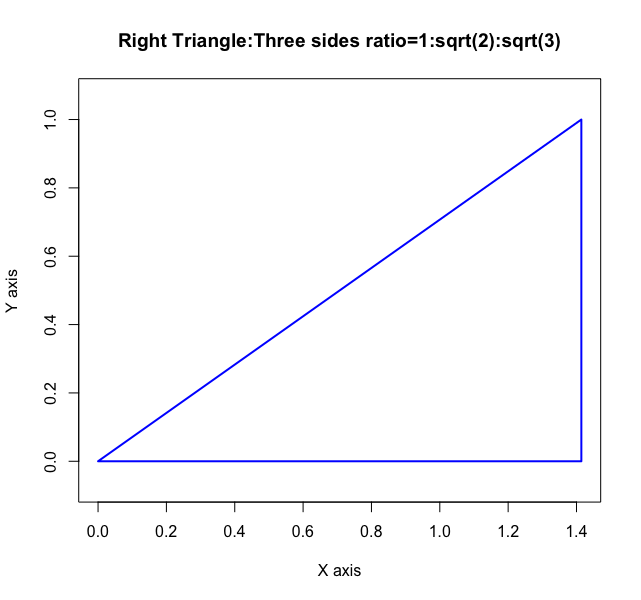
それにつけても「1:sqrt(2)(平方対角線):sqrt(3)(立方対角線)」の直角三角定規が欲しくなる世界。
# "斜辺sqrt(3)"に関する記述が明示的に現れない点に注意。
cx=c(0,sqrt(2),sqrt(2),0)
cy=c(0,0,1,0)
plot(cx,cy,type="l",asp=1,col=rgb(0,0,1),lwd=2, main="Right Triangle:Three sides ratio=1:sqrt(2):sqrt(3)",xlab="X axis",ylab="Y axis")
【オイラーの多面体定理と正多面体】正方形における平方対角線と立方体における立方対角線の関係について。

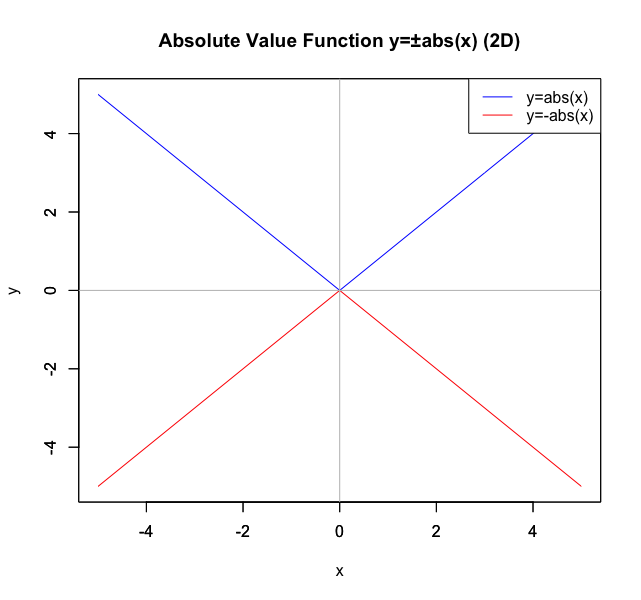
絶対値関数(Absolute Value Function)y=±abs(x)
2次元(2D)…y=abs(x),y=-abs(x)の集合(Set)。
cx<-seq(-5,5,length=11)
cy_plus<-abs(cx)
cy_minus<--abs(cx)
plot(cy_plus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),main="Absolute Value Function x=±abs(y)(2D)",xlab="x",ylab="y", col=rgb(0,0,1))
par(new=T)
plot(cy_minus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),main="",xlab="",ylab="", col=rgb(1,0,0))
# 基準線はx=0,y=0の2本。
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
# 凡例を書き添える 。
legend("topright", legend=c("x=abs(y)","x=-abs(y)"), lty =c(1,1),col=c(rgb(0,0,1),rgb(1,0,0)))
3次元(3D)…y=abs(x),y=-abs(x)の集合(Set)と集合{z}{-z}の積(Product)。

library(rgl)
cx<-seq(-5,5,length=11)
cy_plus<-abs(cx)
cy_minus<--abs(cx)
plot3d(cy_plus,cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_minus,cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(-cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(-5,5),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test20")
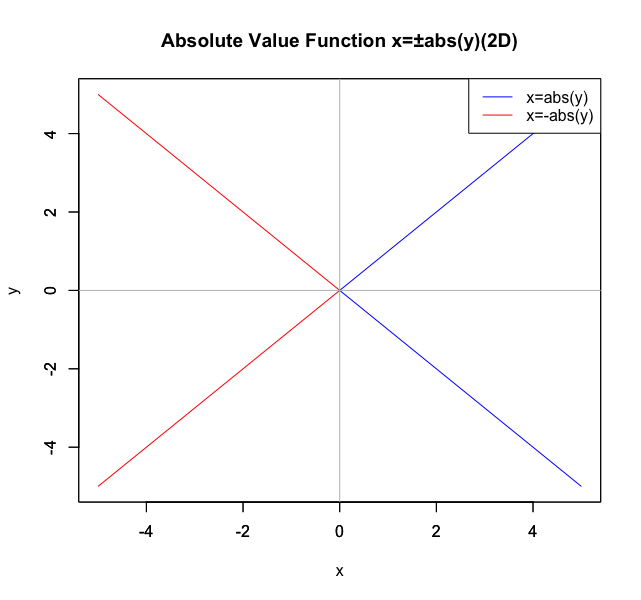
絶対値関数(Absolute Value Function)x=±abs(y)
2次元(2D)…x=abs(y),x=-abs(y)の集合(Set)。
cx<-seq(-5,5,length=11)
cy_plus<-abs(cx)
cy_minus<--abs(cx)
plot(cy_plus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),main="Absolute Value Function x=±abs(y)(2D)",xlab="x",ylab="y", col=rgb(0,0,1))
par(new=T)
plot(cy_minus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),main="",xlab="",ylab="", col=rgb(1,0,0))
# 基準線はx=0,y=0の2本。
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
# 凡例を書き添える 。
legend("topright", legend=c("x=abs(y)","x=-abs(y)"), lty =c(1,1),col=c(rgb(0,0,1),rgb(1,0,0)))
3次元(3D)…x=abs(y),x=-abs(y)の集合(Set)と集合{z}{-z}の積(Product)。

library(rgl)
cx<-seq(-5,5,length=11)
cy_plus<-abs(cx)
cy_minus<--abs(cx)
plot3d(cy_plus,cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_minus,cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(-cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(-5,5),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test20")
共役系(Conjugated System)
これらの関数集合は共役関係(Conjugated Relation)にあったりします。
y=x系…一次関数(Linear Function)x=y=z,x=-y=z,x=y=-z,x=-y=-zなどの集合(Set)

# y=xは何次元に拡張しても1本線のままだが、
# y=-xでは符号を逆転するのがY軸かZ軸かという
# 選択肢が現れる。
library(rgl)
# 関数描画準備
cx<-seq(-5,5,length=11)
cy_plus<-cx
cy_minus<--cx
# 円錐描画
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
crz<-seq(-5,5,length=3000)
f1<-function(x){x}
c0<-f1(seq(-5,5,length=3000))
crx<-Real*c0*sqrt(2)
cry<-Imaginal*c0*sqrt(2)
plot3d(crx,cry,crz,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,0))
# 関数描画
plot3d(cx,cy_plus,cy_plus,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,cy_minus,cy_minus,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_plus,cy_minus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_minus,cy_minus,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(-5,5),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test42")
y=abs(x)系…絶対値関数(Absolute Value Function)abs(x)=y=z,abs(x)=-y=z,abs(x)=y=-z,abs(x)=-y=-zなどの集合(Set)

# y=xは何次元に拡張しても1本線のままだが、
# y=-xでは符号を逆転するのがY軸かZ軸かという
# 選択肢が現れる。
library(rgl)
# 関数描画準備
cx<-seq(-5,5,length=11)
cy_plus<-abs(cx)
cy_minus<--abs(cx)
# 円錐描画
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
crz<-seq(-5,5,length=3000)
f1<-function(x){x}
c0<-f1(seq(-5,5,length=3000))
crx<-Real*c0*sqrt(2)
cry<-Imaginal*c0*sqrt(2)
plot3d(crx,cry,crz,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,0))
# 関数描画
plot3d(cx,cy_plus,cy_plus,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,cy_minus,cy_minus,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(-cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(-5,5),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test43")
x=abs(y)系…絶対値関数(Absolute Value Function)x=abs(y)=z,-x=abs(y)=z,x=abs(y)=-z,-x=abs(y)=-zなどの集合(Set)

# y=xは何次元に拡張しても1本線のままだが、
# y=-xでは符号を逆転するのがY軸かZ軸かという
# 選択肢が現れる。
library(rgl)
# 関数描画準備
cx<-seq(-5,5,length=11)
cy_plus<-abs(cx)
cy_minus<--abs(cx)
# 円錐描画準備
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
crz<-seq(-5,5,length=3000)
f1<-function(x){x}
c0<-f1(seq(-5,5,length=3000))
crx<-Real*c0*sqrt(2)
cry<-Imaginal*c0*sqrt(2)
plot3d(crz,crx,cry,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,0))
plot3d(crx,crz,cry,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=c(200,200,200))
# 関数描画
plot3d(cy_plus,cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_minus,cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(-cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,-cx,cx,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(-5,5),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(-5,-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(5,5),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(-5,5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(-5,5),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test39")
一方、所謂デカルト座標系(Cartesian Coordinate System)には確実に角錐型座標系(Pyramid Coordinate System)Pn(n=-Inf→0→Inf){-Inf^Inf=-Inf,…,-3^3=-9,-2^2=-4,-1^1=-1,0,1^1=1,2^2=4,3^3=9,…,Inf^Inf=Inf}3個の集合(Set)という側面も存在するので色々と矛盾が浮上してきてしまうのですね。
Z軸に沿ったX-Y面を巡る円錐座標系

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}
# トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="",col=c(200,200,200))
# 球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01
points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
# points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
# points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
# points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
# points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
# Rtime01段
# points3d(Real01+2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
# points3d(Real01+2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
# points3d(Real01-2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
# points3d(Real01-2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
# Rtime01+1段
points3d(Real01+2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
# Rtime01-1段
points3d(Real01+2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test91")
X軸に沿ったY-Z面を巡る円錐座標系、あるいはY軸に沿ったX-Z面を巡る円錐座標系

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}
# トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="",col=c(200,200,200))
# 球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01
points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
# points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
# points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
## points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
## points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
# Rtime01段
points3d(Real01+2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
# Rtime01+1段
# points3d(Real01+2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
# points3d(Real01-2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
# Rtime01-1段
# points3d(Real01+2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
# points3d(Real01-2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test92")
自然指数・対数関数(Natural Exponential / Logarithmic Function)y=exp(x),y=log(x)
Z軸はあくまで独立しているので、これを均等尺(Even Scale)から対数尺(Logarithmic Scale)に差し替えると指数関数(Natural Exponential Function)y=exp(x)と対数関数(Natural Logarithmic Function)y=exp(x)の共役関係が表示される事になります。

library(rgl)
# 関数描画準備
cx<-seq(-5,5,length=11)
cy_plus<-cx
cy_minus<--cx
# 円錐描画
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
crz<-seq(-5,5,length=3000)
crze<-exp(crz)
f1<-function(x){x}
c0<-f1(seq(-5,5,length=3000))
crx<-Real*c0*sqrt(2)
cry<-Imaginal*c0*sqrt(2)
plot3d(crx,cry,crze,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(exp(-5),exp(5)),col=rgb(0,0,0))
# 関数描画
plot3d(cx,cy_plus,exp(cy_plus),type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(exp(-5),exp(5)),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(cx,cy_minus,exp(cy_minus),type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(exp(-5),exp(5)),,col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_plus,cy_minus,exp(cx),type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(exp(-5),exp(5)),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(cy_minus,cy_minus,exp(cx),type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(exp(-5),exp(5)),,col=rgb(0,1,0),xlab="",ylab="",zlab="",lwd=2)
texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)
# 中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(exp(-5),exp(5)),col=c(200,200,200),lwd=1)
# 傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
# 傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(exp(-5),exp(-5)),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(exp(5),exp(5)),col=c(200,200,200),lwd=1)
# 傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(exp(-5),exp(-5)),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(exp(5),exp(5)),col=c(200,200,200),lwd=1)
# 傍線Z
lines3d(c(-5,-5),c(0,0),c(exp(-5),exp(5)),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(exp(-5),exp(5)),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(exp(-5),exp(5)),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(exp(-5),exp(5)),col=c(200,200,200),lwd=1)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test51")
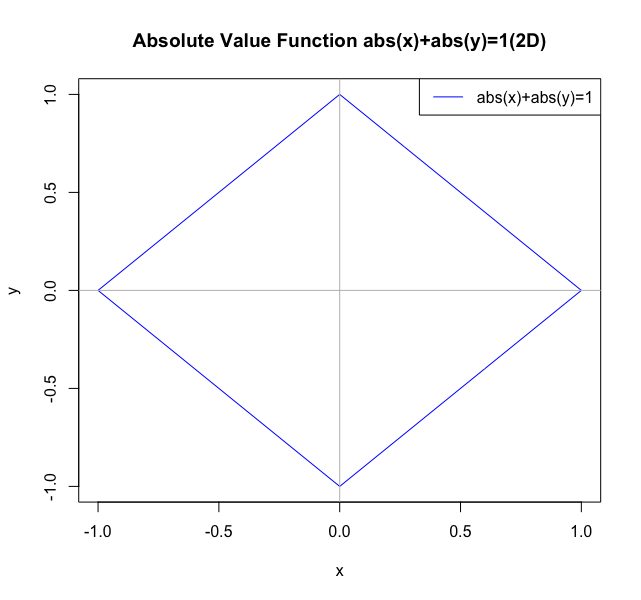
絶対値関数(Absolute Value Function)abs(x)+abs(y)=1
Square_XY<-function(Radius){
c0<-seq(-1,1,length=31)
cx<-c(rev(c0),c0[2:31])
c1<-seq(0,1,length=16)
cy<-c(c1,rev(c1[1:15]),-c1[2:16],-rev(c1[1:15]))
complex(real=cx*Radius,imaginary=cy*Radius)
}
cx<-seq(-5,5,length=11)
cx<-Re(Square_XY(1))
cy<-Im(Square_XY(1))
plot(cx,cy,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Absolute Value Function abs(x)+abs(y)=1(2D)",xlab="x",ylab="y", col=rgb(0,0,1))
# 基準線はx=0,y=0の2本。
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
# 凡例を書き添える 。
legend("topright", legend=c("abs(x)+abs(y)=1"), lty =c(1),col=c(rgb(0,0,1)))
そんな感じで、以下続報…