【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ

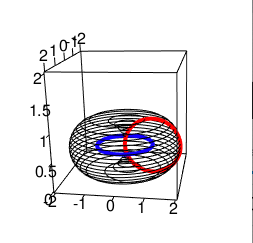
今回の投稿の出発点はこれ。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。

XY軸（円弧）

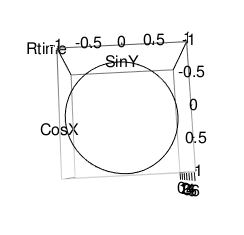
ZX軸（Cos波）

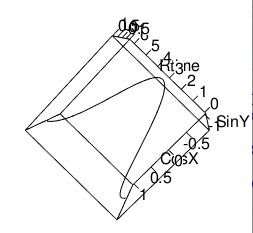
ZY軸（Sin波）

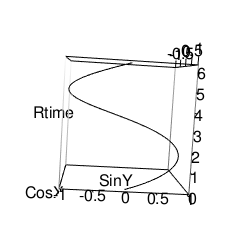
【初心者向け】「単位円筒」から「単位球面」へ

XY面にZ座標に応じた「曲率」を付与。

実は単位円筒(Unit Cylinder)」から拡張可能な立体構造は単位球面(Unit Sphere)だけではありません。
#「トーラス構造」の登場
①まずは平面トーラス（折り返し円柱）を準備する。
トーラス(単数系torus, 複数形tori)-Wikipedia

libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1.5,1.5),ylim=c(-1.5,1.5),zlim=c(-1.5,1.5))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01") 

②平面トーラス（折り返し円柱）の表裏両面に、それぞれ真逆の曲率を付与する。

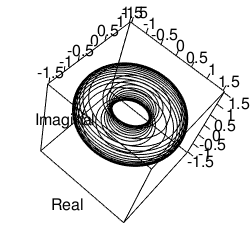
libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
r0<-f0(radians)
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=1500)
c1<-c(f1(c0)/2,-1*f1(c0)/2)
#c1<-c(f1(c0),seq(0,0,length=1500))/2)
r1<-r0*(1+c1)
Real<-Re(r1)
Imaginal<-Im(r1)
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1.5,1.5),ylim=c(-1.5,1.5),zlim=c(-1.5,1.5))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test02") 

例えば時間軸に沿って描画がなされたと想定すると、こう見えたりもします。盃？

libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
r0<-f0(radians)
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=1500)
c1<-c(f1(c0)/2,-1*f1(c0)/2)
#c1<-c(f1(c0),seq(0,0,length=1500))/2)
r1<-r0*(1+c1)
Real<-Re(r1)
Imaginal<-Im(r1)
Rtime<-c(seq(2,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1.5,1.5),ylim=c(-1.5,1.5),zlim=c(0,2))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test02") 

ちなみに大半径(Major Radius)1,小半径(Minor Radius)1の場合。

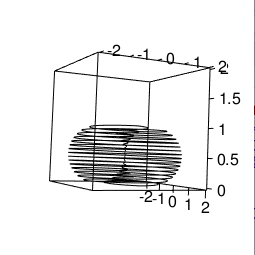
library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}
r0<-f0(radians)
c0<-seq(-1,1,length=1500)
#c1<-c(f1(c0)/2,-1*f1(c0)/2)
c1<-c(f1(c0),-1*f1(c0))
r1<-r0*(1+c1)
Real<-Re(r1)
Imaginal<-Im(r1)
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="")

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/unit07") 

大円と小円を追加する。

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}
r0<-f0(radians)
c0<-seq(-1,1,length=1500)
#c1<-c(f1(c0)/2,-1*f1(c0)/2)
c1<-c(f1(c0),-1*f1(c0))
r1<-r0*(1+c1)
Real<-Re(r1)
Imaginal<-Im(r1)
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="")

#大円描写
Real01<-Re(f0(radians))
Imaginal01<-Im(f0(radians))
Rtime01<-seq(1/2,1/2,length=3000)
points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))

#小円描写
Real01<-Re(f0(radians))+1
Imaginal01<-Im(f0(radians))/2+1/2
Rtime01<-seq(0,0,length=3000)
points3d(Rtime01,Real01,Imaginal01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/unit16") 

座標系(Coordinate System)としては媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表します。

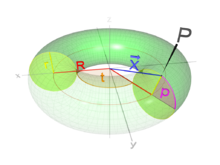
• x=大半径R×cos(t)+小半径r×cos(p)×cos(t)
• y=大半径R×cos(t)+小半径r×cos(p)×sin(t)
• z=小半径r×sin(p)

ここで重要なのが以下。

• 大半径R=0,小半径R=1の時、単位球面(Unit Sphere)を二重に描く。従って経緯度法(経度-180度~180度に対して緯度-90度~90度)や3次元極座標系(水平角φ=-π~πに対して垂直角0~π)は適用範囲を半分に減らしてなお単位球面(Unit Sphere)上の全座標を示せる訳である。
• 逆に大半径R=1,小半径R=0の時、Z=0となってただの単位円(Unit Circle)になる。

そしてこの変遷はオイラーの公式（Eulerian Formula）Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)上における二辺形(Bilateral,NoS=2)すなわち「1辺がπの円弧2分割図形/1辺が2の往復線分」から円そのもの(NoS=Inf(inity))への変遷に合致するのです。
【Rで球面幾何学】二辺形と一辺形？ - Qiita

• この概念上における一辺形(One Side, NoS=1)は「1辺が2πの円弧=円そのもの」であり、ここにある種の循環性を見てとる事が出来そうである。
  一辺形(One Side)Cos(θ)-Cos(θ)i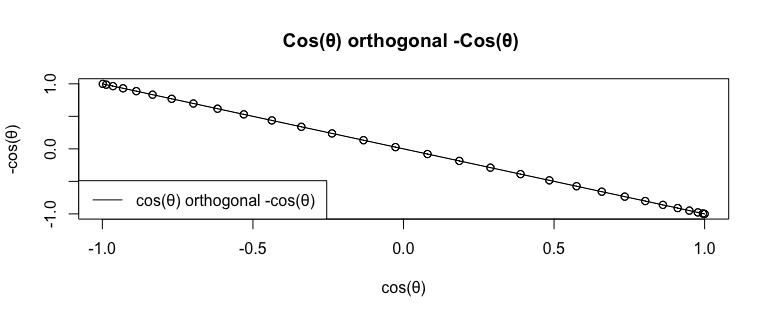
  
  二辺形(Bilateral)Cos(θ)+Sin(θ)i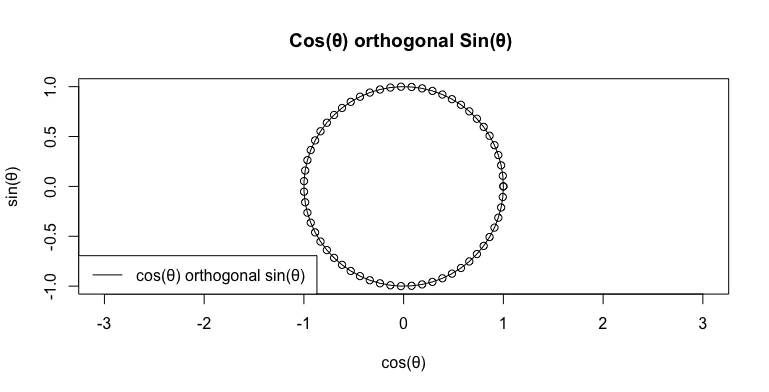
  
  
  円そのもの(Circle Itself)Cos(θ)+Cos(θ)i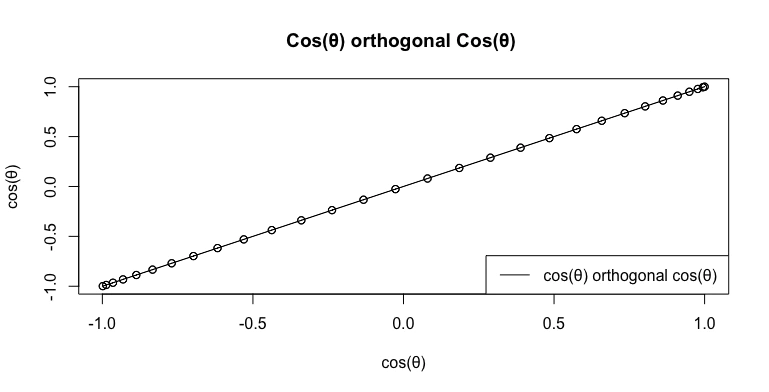
  

これは偶奇性(Evenness)とも連動してくる概念です。
【初心者向け】偶奇性概念と共役関係概念の連続性について。

半径(Radius)1の二重球面たる単位球面(Unit Sphere)から出発します。偶奇性(Eveness)という時、重要なのはそこに現れてる数が偶数/奇数の関係にある事そのものより「ピッチが半周期ズレている」事なんですね。例えば同心円集合(Concentric Circle Set)半径R={0,1,2,3,4,…,Inf(inity)}から出発すると、これを偶数層(Even Layer)として奇数層(Odd Layer)が半径R={0.5,1.5,2.5,3.5,4.5,…,Inf(inity)}という形で現れるのです。
偶数層(Even Layer)0.0-1.0

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#外球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime02<-seq(0,2,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real02<-Real*c01
Imaginal02<-Imaginal*c01
plot3d(Real02*2,Imaginal02*2,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="",col=c(200,200,200))

#内部球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(1/2,3/2,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01
points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test39")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test16")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test19")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test24")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test27")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))
#Rtime01段
points3d(Real01+2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
#Rtime01+1段
points3d(Real01+2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
#Rtime01-1段
points3d(Real01+2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test71")

奇数層(Odd Layer)0.5

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#外球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime02<-seq(0,2,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real02<-Real*c01
Imaginal02<-Imaginal*c01
plot3d(Real02*2,Imaginal02*2,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="",col=c(200,200,200))

#内部球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(1/4,7/4,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01
points3d(Real01*1.5,Imaginal01*1.5,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test41")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写

r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test15")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写

r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test20")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写

r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01+1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01-1,Rtime01,col=rgb(1,0,0))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test23")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01+1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01-1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01,Imaginal01,Rtime01-1/2,col=rgb(1,0,0))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test28")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01+1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test42")

偶数層(Even Layer)0.0-2.0+奇数層(Odd Layer)0.5

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写

r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test17")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写

r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test21")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写

r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01+1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01-1,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test22")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01+1,Rtime01,col=rgb(0,0,1))
points3d(Real01-1,Imaginal01+1,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01-1,Rtime01,col=rgb(0,0,1))
points3d(Real01-1,Imaginal01-1,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01+1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01-1,Rtime01,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test74")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01+1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01-1,Rtime01,col=rgb(1,0,0))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(1,0,0))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test30")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test61")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test32")

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}

#トーラス描写
r1<-f0(radians)
c0B<-seq(-1,1,length=1500)
c02<-c(f1(c0B),-1*f1(c0B))
r2<-r1*(1+c02)
Real02<-Re(r2)
Imaginal02<-Im(r2)
Rtime02<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real02,Imaginal02,Rtime02,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),col=c(200,200,200))

#球面描写
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime01<-seq(0,1,length=3000)
c0A<-seq(-1,1,length=3000)
c01<-f1(c0A)
Real01<-Real*c01
Imaginal01<-Imaginal*c01

points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01+1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01+1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01+1,Rtime01-1/2,col=rgb(1,0,0))
points3d(Real01-1,Imaginal01-1,Rtime01-1/2,col=rgb(1,0,0))
#Rtime01段
points3d(Real01+2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01,col=rgb(0,0,1))
#Rtime01+1段
points3d(Real01+2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01+1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01+1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01+1,col=rgb(0,0,1))
#Rtime01-1段
points3d(Real01+2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01,Rtime01-1,col=rgb(0,0,1))
points3d(Real01,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01+2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01+2,Rtime01-1,col=rgb(0,0,1))
points3d(Real01-2,Imaginal01-2,Rtime01-1,col=rgb(0,0,1))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test34")

それにつけても何かを連想させませんか？　そう、立体充填性(Space filling)における正四面体(Regular Tetrahedron)と正八面体(Regular Octahedron)の相補関係です。
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…

あれ、数論(Number Theory)の話をしてた筈なのに、いつの間にか分子構造(Molecular structure)みたいな世界に足を踏み入れている!!