【Rで球面幾何学】二辺形(Bilateral)と一辺形(One Side)？

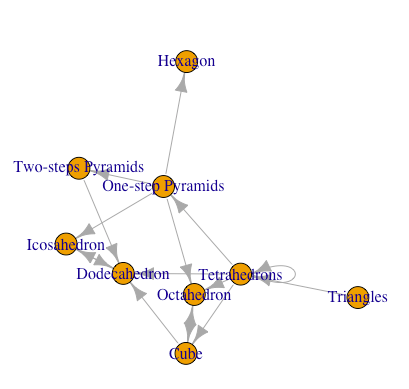
最近取り組んでいた投稿に一区切りついたので、これからはいよいよ昔年の課題だった以下の「立体未満の図形」について考える機会が増えそうです。
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…

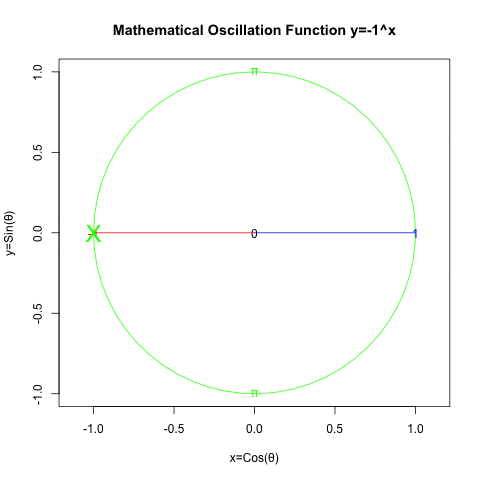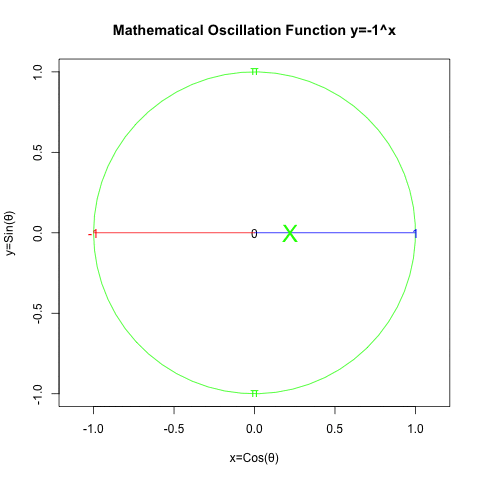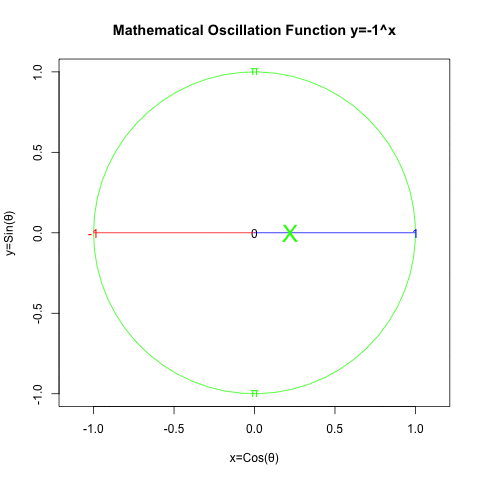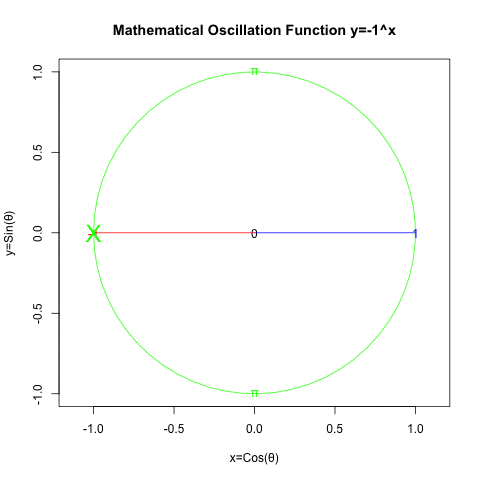
• 二辺形(Bilateral)…断面数0、頂点分布[1,1]。これはパスカルの三角形2段目の数字に合致する。立方対角線1本。一言で要約すると「頭蹠と対蹠を結ぶ立方対角線上の往復」
  
• 一辺形(One Side)…断面数0、頂点分布[1]。これはパスカルの三角形1段目の数字に合致する。立方対角線0本。一言で要約すると「対蹠と対応付けられてない頭蹠より伸ばされる任意の(走査)線」
  

つい手癖で滑らかにアニメーションさせてしまってますが、その時点で既に意味論的統制(Semantic Control)の許諾を受けた虚理の世界(Imaginary Set)が始まってしまってる訳です。

• 「1,2,3,…,∞」の範囲を扱う「自然数の世界(Natural Number Set)」に0とマイナスの概念(Concept)を導入(Intoroduce)し「整数の世界(Integer Number Set)」に。
• さらには比(Ratio)で表現(Expression)可能な有理数（Rational Number）と、それとは別途個別の定義(Definition)に頼る無理数（Irrational Number）の概念を導入し「実数の世界(Real Number Set)」に。
• ところが、まだまだ「数直線の連続性(Number line Continuity)」が完全に満たされたとはいえず、人類はさらに虚数(Imaginary Number)概念を導入して「複素数の世界(Complex Number Set)」に足を踏み入れた。有理数までの世界を「計数可能な世界(Countable Set)」とするなら「虚理の世界(Imaginary Set)」は「計算自体は可能な世界(Computable Set)」。「限られた計算リソースを巡る絶え間なき鬩ぎ合い、その一方での（常用対数表やコンピューターの発明といった）既存の前提を吹き飛ばす定期的イノベーション」に振り回され続ける。

こういう問題提起もありますね。
【対訳版】ユージン・ウィグナー『自然科学における数学の理不尽なまでの有効性(1959年)』

第一の点は、〈数学の概念は、まったく予想外のさまざまな文脈のなかに登場してくる〉ということ。
The first point is that mathematical concepts turn up in entirely unexpected connections.
しかも、予想もしなかった文脈に、予想もしなかったほどぴったりと当てはまって、正確に現象を記述してくれることが多いのだ。
Moreover, they often permit an unexpectedly close and accurate description of the phenomena in these connections.
第二の点は、予想外の文脈に現れるということと、そしてまた、数学がこれほど役立つ理由を私たちが理解していないことのせいで、〈数学の概念を駆使して、なにか一つの理論が定式化できたとしても、それが唯一の適切な理論なのかどうかがわからない〉ということ。 
〔Secondly, just because of this circumstance, and because we do not understand the reasons of their usefulness, we cannot know whether a theory formulated in terms of mathematical concepts is uniquely appropriate.
〔この二つの論点をさらに言い直すと〕第一の点は〈数学は自然科学のなかで、ほとんど神秘的なまでに、途方もなく役立っているのに、そのことには何の合理的説明もない〉ということ。
The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.
第二の点は〈数学の概念の、まさにこの奇怪な有用性のせいで、物理学の理論の一意性が疑わしく思えてしまう〉ということ。
Second, it is just this uncanny usefulness of mathematical concepts that raises the question of the uniqueness of our physical theories.

要するにポパーの反証可能性（Falsifiability）担保論を持ち出すまでもなく「誰も(計算自体は可能な世界における)正解なんて知らない」という冷徹な現実。「サイバネティックス概念の提唱者」ノーバート・ウィーナー（Norbert Wiener,1894年~1964年）も「誰も科学は最終的には分からん。せいぜい使い慣れるのが精一杯」と、すっかり匙を投げていたといいます。近代に至るまで「(全ての誤差を克服する方法さえ見つかれば)あらゆる計測結果が最終的には一致する筈だ」なる信念こそが科学研究の原動力となっていた側面が確実にあったのですが、今から思えばまさにその思いこそが「虚理の世界(Imaginary Set)」からの呼び声に迂闊に応えた産物だったとも…(コンドルセ伯爵やジョン・スチュワート・ミルの様な数学者=古典的自由主義者も例外ではなさそうなのが辛いところ)

かかる「虚理(Imaginary Things)」の大源流を遡ると、0を原点に無限大(Inf)と無原小(-Inf)の双方向に伸ばされた半直線が無限に直交(-InfOrthogonal)し続ける平方眼(Square Grid)や立方眼(Cubic Grid)で構成される「デカルト座標系の世界(Cartesian Coordinate System Set)」そのものにまで行き当きそうです。決してその直交性と座標軸としての有効性を疑われない「絶対真理の天秤」。そもそもの起源からして古い…

①カンブリア爆発期（Cambrian Explosion、葯5億4200万年前〜5億3000万年前）、視覚と関連情報を処理する脊髄=中央情報処理器官(Central Infomation Processing Organ)」を獲得し（四肢を生やし）前後上下左右の感覚に従って俊敏な動作をこなす様になった左右相称動物（Bilateria）が、トレンドに乗り遅れ相変わらず鈍重なままの放射相称動物（Radiata）に進化面で優位に立ち始めた。

• 逆を言えば、それ以前の時代の生物は、まだまだ前後上下左右の感覚に従って自らの運動を制御する中枢神経をちゃんとした形では備えていなかった。すなわちデカルト座標系も(観測結果の蓄積とその分析に立脚する)科学的思考様式も、それをサポートするコンピューター・システムの類もそれ以前の時代には原型すら存在していなかったと考えるのが自明の場合(Trivial Case)といえよう。

②一方、かかる新能力を初めて捕食動物として有効活用し、一旦は「（当時の生物としては破格の大きさまで成長する）地球最初の百獣の王」の座に躍り出たアノマロカリス（Anomalocaris、約5億2,500万〜約5億0,500万年前）なる生物は、その一方で最後にはあえなく滅び遺伝子的痕跡を後世に一切残す事なく地上から消え去った。

• そもそもどうしてアノマロカリスは滅びたのか。ある考え方によれば、皮肉にもこの捕食性動物は、その奇跡的成長ゆえに「（棘や殻や毒で自衛した）食えない連中」ばかり淘汰して狩果を先細らせる一方、原始的な魚類の先祖といった競争相手の進化ラッシュを引き起こしてしまったのだという。その感点から「あらゆるビジネスモデル（および歴史的事象）の先例」と皮肉る向きもある。
• ある意味、この概念化は旧約聖書に反面教師的に記されている「絶対暴君二ムロド」のそれに近い。そこから出発して中世には「領主が領民と領土を全人格的に代表する農本主義的権威体制」が覇を競い合い「国家経営上、十分なだけの火力と機動力を備えた常備軍を中央集権的官僚制が徴税によって賄う主権国家が登場し国内における暴力的手段を必要なだけ独占する法実証主義に拠って鬩ぎ合う国際協調体制(17世紀〜1910年代)」が最終勝者となって「国家同士の競争が全てとなる総力戦時代(1910年代後半~1970年代)」に至ったという考え方すら出来てしまう。
• この次元における意味論的統制(Semantic Control)は単純極まりなく「タフでなければ生き残れない。タフなだけでは生き残る資格がない」程度なのだが、その世界においてさえ現実にはどうしても後世の人間が日本の平氏やフランスのブルグンド王国やリュジニャン家、神聖ローマ帝国のホーエンシュタウフェン朝の滅亡に納得がいかずこれに取材した文学作品を上梓し続けている。
• そういえばフランスでもドイツでも社会学成立の契機となったのは19世紀後半に産業革命浸透が引き起こした伝統的地方共同隊の崩壊だったが、前者が共同体((Ascension)こそ社会の実体と考えてその再建を志向したのに対し、後者は権力や環境が個人の生活に及ぼす影響に関心を集中させた辺りに最初の個性が現れたとも。パスツール(1822年~1895年)やコッホ(1843年~1910年)の細菌学や衛生学。統計力学に電磁場理論。シャルコー(1825年~1893年)の催眠療法にフロイト(1856年〜1939年)の夢分析。タルド(1843年~1904年)の模倣社会学。果ては新興資本家が経済的成功を収める一方貧富格差が拡大したのを受けて「金持ちからしか盗まない変装名人の義賊小説」が大ヒット。金持ちになって盗まれる側に回った作者が毎晩悪夢にうなされる様になるオチがついた展開まであったという（モーリス・ルブラン症候群）。こうして誰もが「目に視えない何か」との共存を強要されながら暮らす様になったまさにその時代、軍隊や医療や都市再開発の近代化に行動指針を与える役割を担った統計学の大躍進が始まった訳である。やはり果たしてデカルトの信仰的態度や天体観測結果の誤差除去が最大の悲願だった時代の一波一絡げ主義から完全には脱却出来ていなかった側面も…まぁハミルトンの四元数(Hamilton's Quaternions)やベイズ推定（Bayesian Inference）の全面否定に向かう時代の世相とはそういう世相だったという話でもある。「今は変わった」といいますが、果たして何がどう変わったやら…
  統計学入門「主義」 を心配するみなさまに

どうも「デカルト座標系の世界」には、その「絶対真理の天秤」性故に使用者の主義主張に絶対の確信を与えてしまう側面がある様なのです。ともすればオライリーの機械学習参考書とかに目を通している時にすらそれを感じてしまう時が…「おいおい、そのデータの評価軸、本当に直交してるの？ 成果を出すのを急ぎ過ぎてるのでは？」みたいな…最近はこの世の価値観の衝突の大半はこれが原因じゃないかと感じる時すらあります。そしてこの基準に従わない「(ハミルトンの四元数やベイズ推定の様な)計算自体は可能な世界(Computable Set)」に固有の拒絶感を示すとも…

ところでこの概念には前傾の二辺形や一辺形は円描画関数（Circle Function）Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)で最初に邂逅したのです。辺数の判別式としても使え、例えば角度としてθ=0~πの周期を与えた場合は1がその答え。

WEA<-function(x_min,x_max){
c0<-seq(0,2*pi,60)
f0<-function(x){cos(c0)+cos(c0-pi/x)}
plot(f0,xlim=c(x_min,x_max),main="When Euler's formula appear?",xlab="NoC(Number of Corners)",ylab="cos(θ)+cos(θ-π/Noc)")
abline(h=1,col=rgb(1,0,0))
}

１辺形（One Side）以上の世界ではこの条件を満たすのは2辺形（Bilateral）のみ。以降はこの判別式の上限たる2に向けてゆっくり収束していきます。

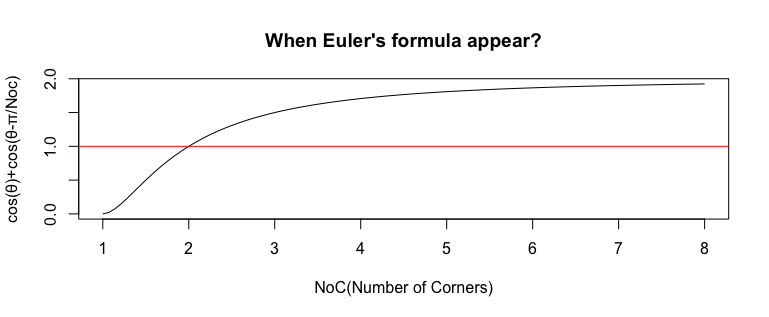
WEA(1,8)

一方、１辺形（One Side）未満の世界ではこの条件を満たす図形が出現周期を短縮しつつ、この判別式の下限たる0に向けて無限に現れ続けるのです。

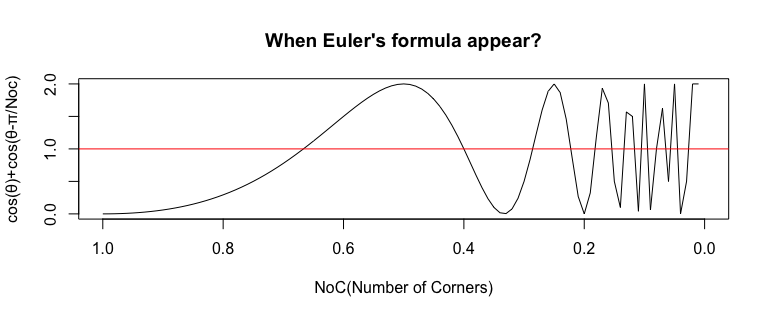
WEA(1,0)

具体的にこの条件を満たすのはNoS=2/(2N+1)の条件を満たすケース。すなわち2辺形、2/3辺形、2/5辺形、2/7辺形…と出現周期を短縮しつつ0に向けて収束していきます。

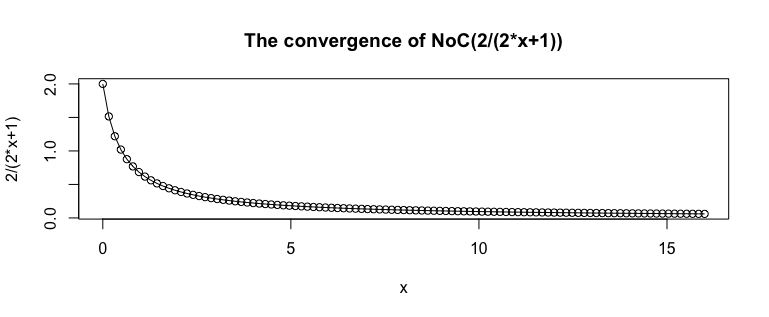
複素平面（Complex plane）上でも確認してみましょう。まずはそれぞれの極限状態のシミュレーション…

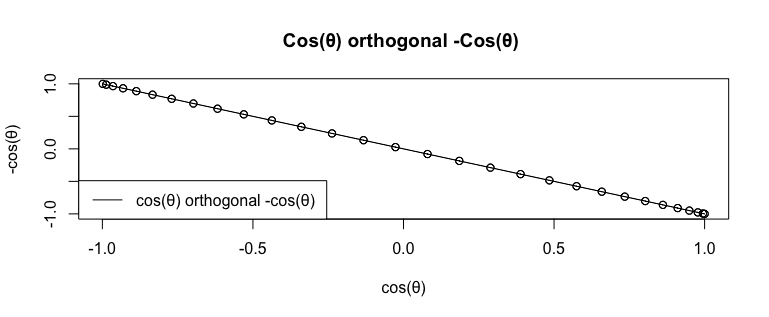
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)*-1
plot(cx,cy,type="o",main="Cos(θ) orthogonal -Cos(θ) ",xlab="cos(θ)",ylab="-cos(θ)")
#凡例
legend("bottomleft", legend=c("cos(θ) orthogonal -cos(θ) "), lty=c(1), col=c(rgb(0,0,0))) 

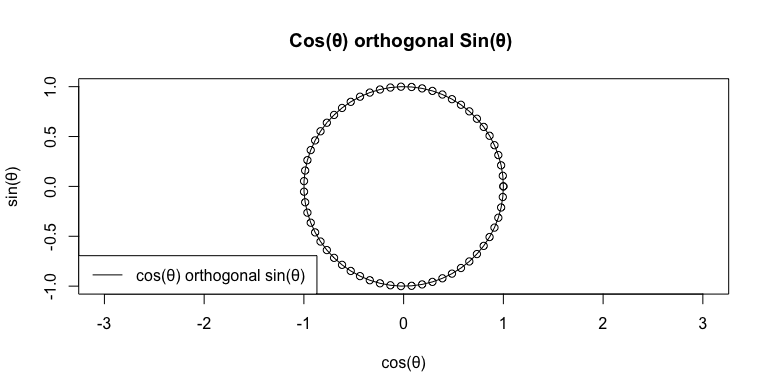
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="o",main="Cos(θ) orthogonal Sin(θ) ",xlab="cos(θ)",ylab="sin(θ)")
#凡例
legend("bottomleft", legend=c("cos(θ) orthogonal sin(θ) "), lty=c(1), col=c(rgb(0,0,0))) 

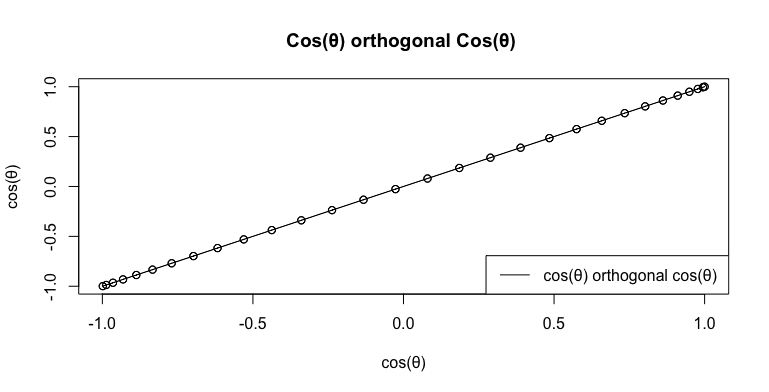
#円そのもの(Circle itself)
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)
plot(cx,cy,type="o",main="Cos(θ) orthogonal Cos(θ) ",xlab="cos(θ)",ylab="cos(θ)")
#凡例
legend("bottomright", legend=c("cos(θ) orthogonal cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))

大体、どういう範囲で動くのかは見切れましたね。それでは実践…

#FHtD=1角形から2角形へ（From Henagon to Digon）
#Noc=角数(Number of corners)
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)

#中心からの補助線
cx0<-rep(0, length=length(cx))
cy0<-rep(0, length=length(cy))
segments(cx0, cy0, cx, cy,col=c(200,200,200))

#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}

1角形〜円そのものへ（あまりに収束が遅いので途中で加速している）

#アニメーション
library("animation")
Time_Code=c(seq(1,6, length=50),seq(6,64,length=20))
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")

予測通り「円盤が回転速度を落としつつゆっくり回っていく」情景が顕現しました。一方、1辺形以下の動きはこうなります。

#アニメーション
library("animation")
Time_Code=seq(1,0.1,length=41)
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")

こちらも予測通り「円盤が回転速度を上げながら旋回している」情景となりました。これが「計算なら可能な世界」にありがちな展開で、どうもこの式、思わぬ方向に繋がっていく様な…
【Rで球面幾何学】「単位円筒」から「トーラス構造」へ


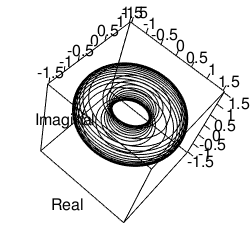
そんな感じで以下続報…