以下の投稿に「関数列(Function Sequance)の基底(Basis)」なる概念が登場しました。まずこれが何を意味するかを明らかにしないといけません。
【無限遠点を巡る数理】等差数列と等比数列①関数列との関係は?
基底ベクトル(Basis Vector)と基底関数(Basis Function)
線形空間Vを格子状に“番地付け“するベクトルの組である。
①例えばxy座標系は(1,0)(0,1)の組をこれに選び、X座標やY座標をそのスカラー倍で表現したものと見做す。
定義としては線形空間V上のr個のベクトルの組が次の性質を持つ時、それをベクトル空間の基底(Base/Basis)という。
①互いに1次独立(Linear Independence)である。
線型独立 - Wikipedia
②線形空間V上の任意のベクトルが一次結合(Linear Combination)ax+by+cz…の形で一意に表される。このことを 空間Vを張っている(格子を生成する上で必要なものが全て揃っている)という。
ベクトル空間 - Wikipedian次元空間を表現するにはn個の1次独立なベクトルが必要となる。また特にベクトルのノルムが1で、どの2つのベクトルも直交(Orthogonal)している場合を正規直交系(ONS=OrthoNormal System)という。
何の事もない、ある意味複素数X+Yi概念の抽象化ですね。その結果、線形代数学(Linear Algebra)の世界では「基底ベクトルの変換」なる概念が追加されます。
基底ベクトルの変換 - EMANの物理数学

基底関数(Basis function)-Wikipedia
関数空間の基底ベクトルのことである。すなわち対象となる空間に属する全ての元(関数)は、この基底関数の線型結合で表される。
例えば、実数値関数のフーリエ変換(コサイン変換・サイン変換)ではコサイン関数もしくはサイン関数、ウェーブレット変換ではウェーブレット関数とスケーリング関数、スプライン曲線では区分的多項式が基底関数として用いられる。
フーリエ変換 - Wikipedia
ウェーブレット変換 - Wikipedia
スプライン曲線 - Wikipedia
この考え方を援用すると複素指数関数型フーリエ級数展開では(コサイン関数概念とサイン関数概念関数の双方を含む)自然指数関数exp(θi)が基底関数と見做される様です(基底概念のパラダイムシフト?)。ここで忘れてはならないのが「乗法群の演算においてはスカラー倍といっても、それが添字単位、周期単位ともに-Inf→0→Infの範囲の均等尺上でなく、それを0→1→Infの範囲に射影した対数尺上で遂行される」なるルール。
【初心者向け】フーリエ解析を可視化する。
三角波(Triangular Wave)の場合(実数部に現れる)



放物線(Parabola)の場合(実数部に現れる)



ノコギリ波(Sawtooth Wave)の場合(虚数部に現れる)



矩形波(Square wave)の場合(虚数部に現れる)

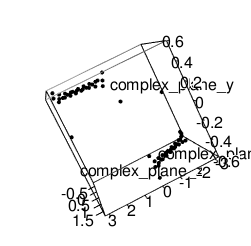


- あくまで「有意水準を満たすレベルまで波形を重ねて近似した」だけの話なので(無関係の波をさらに相応の数だけ重ね)大数の法則」で押し潰す(あるいはもっと手っ取り早く逆波形を掛ける)事で(基底たる)円状態e^θiの状態に戻す事が出来る(線形代数学における規定ベクトル変換の概念に対応するかもしれない振る舞い?)。
- そもそも狙う波形が(Cos波に対応する)実数面や(Sin波に対応する)虚数面に現れるという時点でフーリエ変換なる近似技法自体に観察者の主観性に依存する部分が存在する?
- またフーリエ変換は、解析学の進歩に合わせその計算対象区画を指定区域内(定積分の概念に対応する有限範囲)、周期1の無限反復(単位トーラスの概念に対応)、(無限小-Infから無限大Infの範囲を扱う)繰り返しなき無限範囲(広義積分の概念に対応。無限遠で無限大と無限小が連なる無限大トーラス構造とも見做せる)と拡張してきた事でも知られる。この部分は以下に述べる「近世から近代にかけて急速に発達した数理の集大成」すなわちオイラー座標系(Euler Coordinate System)における一次元認識とも重なってくる。
【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ

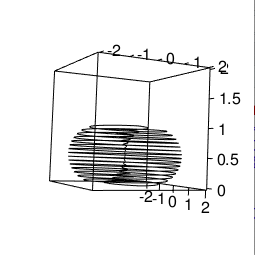

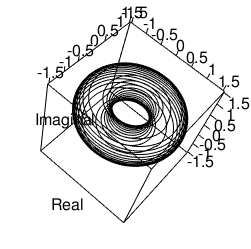
函数近似において、各々適当な点に関して球対称となる実数値函数からなる基底を考えるとき、各基底函数は放射基底関数(RBF=Radial Basis Function、動径基底関数)と呼ばれる。一般に、函数φが動径函数あるいは球対称(Radial)であるとは、φ(x)=φ(‖x‖), すなわちその値が偏角成分に依存せず動径成分(つまり原点からの距離)のみに依存して決まることを言う。従って動径基底函数は適当な点cを中心として、cからの距離のみに依存して決まる (φ(x;c) = φ(‖x−c‖))。ここで、ノルムはふつうユークリッド距離で考えるが、べつの距離函数を取ることもできる。
要するにピタゴラスの定理(Pythagorean Theorem)y=sqrt(1-x^2)の基底関数化。実際には用途に応じて様々な円関数が用いられます。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

単体としての見え方はこんな感じ。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ


機械学習分野で活性化関数(Activation Function)として用いる場合の合成方法についての勉強はこれからですが、イメージ的にはおそらく任意の半径の円関数を数直線上の任意の位置に置いていく形で欲しい波形を近似していく感じ?(おそらく円関数の数と半径と中心位置の算出辺りが学習対象)。以下に述べる「近世から近代にかけて急速に発達した数理の集大成」すなわちオイラー座標系(Euler Coordinate System)が想定していたより複雑な対象を扱う様になった為に周期の概念の撤廃を余儀なくされたとも見て取れますね。
オイラー座標系(Euler Coordinate System)の場合①前提となる出発点と問題意識
それでは私がオイラー座標系(Euler Coordinate System)の名前で編纂しつつある「近世から近代にかけて急速に発達した数理の集大成」カテゴリーと突き合わせてみましょう。ちなみに前提としてとりあえず以下の諸概念は最初から(要するにカンブリア爆発期における視覚とその情報を処理する脊髄を獲得して以降の進化の遺産たる)形相(Eidos/Form)として獲得済みとします。
- 自然数集合(Natural Set)…初項(First Term)1/公差(Common Difference)1の等差数列(Arithmetic Sequence=算術数列)Nn(n=1→Inf){a0,an+(n-1)d,…}(ただしa0=初項,d=公差)={1,1+1=2,(1+1)+1=3,…,n}の形で規定される。ただし線形性|x+y|=|x|+|y|の代わりに三角不等式|x+y|≦|x|+|y|が成立する次元(すなわち1次元以上)においては「次に置かれる1」が同じ線上に置かれる保証が与えられないものとする(すなわち別途検証が成立するまで「半径の2倍が直径である」事が自明の場合とならないと考える)。
-
十進法(Decimal System)…10を法とする剰余類{0,1,2,3,4,5,6,7,8,9}を周期単位(Cycle Unit)/添字単位(Index Unit)に採用し桁数だけ入れ子状態にする事で小数点下も表せる様にした画期的発明。山本義隆「少数と対数の発見(2018年)」によれば欧州全域にこれが広まったのはイタリア・ルネサンスを経た後の宗教戦争の時代だったという(16世紀後半~17世紀初頭)。まさしく近世以降の数学の急発展に欠かせない道具立てだったのである。
「数学の常識」が確立したのは意外に新しい
【初心者向け】N進法(N-ary)とp進数(p-adic)

- (前後上下左右を峻別する動物的感覚に由来する)N次元が重層するイメージ…既にデカルト座標系(Cartesian Coordinate System)にその名を冠するルネ・デカルトが「方法序説(Discours de la méthode,1637年)」の中で平面上の座標の概念を発表済みだったが、彼自身は(ベクトル空間や線形代数といった概念の大源流となった)複素数表現に懐疑的で、極座標系(Polor Coordinate System)概念との統合が図られたガウス平面(Gaussian plane=複素数平面)の概念が登場したのはフランス革命期~ナポレオン戦争時代(18世紀末~19世紀)に入ってからとなる。発案の発端となったのはオイラーの公式(Eulerian Formula,公式発表1748年)exp(θi)=Cos(θ)+Sin(θ)i発案の契機ともなった「(マクローリン級数による)高階微積分に伴うCos波やSin波の回転イメージ(元座標に複素数(0±1i)を掛けた場合に相当。回転行列の概念の大源流?)」とも?
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」?



回転行列が なぜ あの形なのか数学の素人が考える
複素数表現a+biを出発点とする線形結合表現ax+byは機械学習分野で活性化関数として活躍するシグモイド関数**(Sigmoid Function)S(x)=1/(1+exp(−(ax+b)))(aが傾き、bがバイアスを定めるパラメーターでこの線形変換型が学習対象となる)にも影を落としている?
シグモイド関数の傾きとバイアスを変える
【初心者向け】ロジスティック方程式とその関連範囲
ところで最初に観念的難関として立ちはだかるのは、当初(それ自体は観測対象とならない)観測原点(Observation Origin)と観測限界=無限遠点(Observation Limit=Inf(inity))の間に分布する有限の観測結果集合(Observation Result Set)が片側無限数列(One Side Inf(inity) Sewguance)およびそれを半径(Radius)とする観測円(Observation
Disk)/**観測球(Observation Ball)**しか形成しない事です。
【無限遠点を巡る数理】等差数列と等比数列①関数列との関係は?

これをどうしたら0を中心に両端に無限小-Infと無限大Infを配した両側無限数列直径(One Side Infinity Sewguance)へと発展させられるでしょうか。すなわち幾何学でいうところの直径(Diameter)概念の導入。統計学でいうところの比例尺度(Ratio Scale)概念の導入。それかが最初の課題となる訳です。

オイラー座標系(Euler Coordinate System)②中心の検出と誤差の切り捨て(0次元-0.5次元=点/同心円/同心球面空間)
近世から近代にかけての数学者は中心極限定理(CLT=Central Limit Theorem)に従ってこう考えました。
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史
- 小さな誤差ほど比較的観測され易い。
- 大きな誤差ほど比較的観測され難い。
- かかる観測結果集合は出現確率によって同心円集合(Homocentric Circle set)/同心球面集合(Homocentric sphere set)を形成し、中央ほど密集する。
今日でいう確率密度空間(Probability Density Space)概念の大源流ですね。ならばとりあえず観測結果集合から平均(Mean)を求め、それを中心に定めれば良いのです。
【初心者向け】記述統計学と代表値




この考え方では観測結果集合の規模が大きいほど中心の推定位置も安定しますが、それでも平均値を求める計算の都合上、どうしても外れ値(Outliers)の影響を色濃く受けてしまいます。そこでガウスは数理的基準に従って一定以上の外れ値を誤差を切り捨てる誤差関数(ERF=Error Function)と相補誤差関数(ERFC=Complementary Error Function)を発表しました。正規分布(Normal Distribution)概念の出発点ですね。
外れ値と判定する方法と、外れ値の除去について
【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。
【初心者向け】正規分布とは何か?
- あくまで天文学者として観測精度(Observation Accuracy)を高めるべく事しか考えていなかったガウスは、本当に「誤差は正規分布する」事実を発見したに過ぎず「(後世における帰無仮説の棄却によって)有意の外れ値を検出して役立てる」といった類の発想は一切持たなかった。そうした考え方が急浮上してくるのはあくまでは19世紀後半、貨幣経済の浸透と産業革命の導入によって近世までは形骸化しつつも建前上はそれなりの形で継承されてきた既存の身分社会や地方共同体が存続を許されなくなって以降であり、幸いにもその時代には既にガウス(Carolus Fridericus Gauss、1777年~1855年)はもはや生きてはいなかったのである(同時代に生き、同じ復古王政時代の王党派として自然に口を突いて出た王権擁護の主張の数々がキェルケゴールやカール・マルクスの様な新進気鋭の後続に徹底して叩かれ続ける「ヘーゲルの悲劇」とも無縁で済んだ)。一方、その19世紀後半に勃興した統計学や社会学は(王侯貴族や聖職者/士官/官僚供給層といったランティエ(Rentier、地税や家賃収入で暮らす不労所得者)の如き、収入制限選挙時代には議会政治を牛耳る事も可能だった)既存ブルジョワ=インテリ=政治的階層の存続を賭した自己正当化(実際それまでの科学と技術と芸術の発展はベルヌーイ一族やフラゴナール一族の様な名家と彼らへのパトロネージュに支えられてきたのではなかったか?)と「教育の平等と性差別撤廃こそが天才発掘の可能性を最大化する」と考えたコンドルセ伯爵(Marie Jean Antoine Nicolas de Caritat, marquis de Condorcet, 1743年~1794年)やジョン=スチュワート=ミル(John Stuart Mill,1806年~1873年)の様な古典的自由主義者(Classical Liberalist)=数理的大同主義者(Mathematical Daidoist)の闘争の渦中に否応なく巻き込まれていく。
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史 -
ガウスは最小二乗法(Least Squares Method)の発案候補者の一人とも目されているが、これもまた天文学者としての研究の一環であった。
回帰分析(単回帰分析)をわかりやすく徹底解説!
【初心者向け】記述統計学と代表値
-
平均でなく(外れ値の影響を受けにくい)中央値(Midian)や最頻値(Mode)を代表値(Representative Value)に選ぶ発想が生まれてくるのもまた、後世になって(人間社会の実測データといった、より複雑なデータを扱う様になった)統計学が発達して以降となる。
【初心者向け】平均と標準偏差、中央値と平均偏差
【初心者向け】度数分布/度数分布図と最頻値
こうして同心円集合の抽出に成功して初めて、全体像を放射基底関数ないしは複素円関数-1^x=(0±1i)^2x(左式に-1=i^2を代入した結果)で表現可能な演算結果集合(Operation Result Set)として把握可能となるのです。なおこの時点ではまだこの座標系には実数軸(Real Axis)が1本も存在しておらず、虚数軸(Imaginal Axis)のみが存在している形となります(0.5次元)。
- そして線形代数学が発達して線形変換の固有値(Eigenvalue)や固有ベクトル(Eigenvector)の研究が進むと、これを援用する形で(相関係数概念と深い関わりを要する)楕円関数(Elliptic Function)や主成分分析(PCA=Principal component analysis)の概念が追加される展開を迎える。
線形代数の基礎 第12回 - 固有値・固有ベクトル
線形代数の基礎 第13回 - 対角化
【初心者向け】方形描画関数②距離空間(Metric Space)との関係。
ところで上掲のERF/ERF関数図は円外周を無限遠点に設定しているので「重力レンズ効果によって球面の裏側まで見通せるブラックホールと同じ見え方」をしています(それでも全体が球面の様に見えているのは、観測者側が主観的に辺縁部の余分な「等高線」を誤差としてしまう為)。実は直径=両側無限数列の概念導入によってこの「見え方」は失われてしまうのです。
オイラー座標系(Euler Coordinate System)③実数列(Real Line)の概念追加(1次元-1.5次元=線/円柱/同心トーラス空間)
1の原始冪根を演算に選んだガウスの巡回群Z^n=1ではn=2の時{1,-1}、n=4の時{1,i,-1,-i}が元となります。
1の冪根 - Wikipedia
この考え方に従うなら、1次元は実数列(Real Line)、すなわち無限連続等比数列(Infinite Continuous Geometric Progression=無限連続幾何数列)たる1^x(y=(1+0i)と-1^x(y=(0+1i))の接点として規定されなければいけません。ただし後者のピッチは2なので規則正しく離散的な公差(Common Difference)1の等差数列(Arithmetic Sequence=算術数列)を得る為に偶奇一対(Parity Set)で扱う必要が出てきます。
【無限遠点を巡る数理】オイラー座標系②複素等比数列による整数概念の再構築。


- あるいは「関数-1^xにおける(±1+0i)⇄(0±1i)⇄(∓1+0i)の繰り返しの実数部のみを取り出して周期単位とする事で、交差1の等差数列を得る」とも考えられるが(この場合、定数関数x=0が基準線として通る)、この場合も0を原点とする偶数系(Even System)と-1/1を原点とする奇数系(Odd System)の同時成立は避けられない。
いずれにせよこの段階における数理では実数部における添字単位の一次元上の増減のみが重要で(それを導出するのに用いられる)周期単位虚数部の演算は様々な形で想定され、かつ最終的には切り捨てられるのです。例えば上では円形関数y=-1^xを想定しましたが、これを方形関数x+y=1に置き換えても構いません。この辺りの「最終的に計算が合っていれば導出過程を問わない」自由度の高さが虚部の虚部たる由縁。要するに補助線に過ぎないのです。【初心者向け】方形描画関数①三角関数との関係。

- この考え方を極限まで押し進めたのが「‖x‖=0⇄x=0(演算結果集合の数だけ零元が存在する)」「‖ax‖=|a|‖x‖(スカラー倍演算が成立する)」「‖x‖+‖y‖≧‖x+y‖(三角不等式が成立する)」を三大成立条件とするノルム空間(Norm Space)概念であり、実数の範囲を‖x‖+‖y‖=‖x+y‖から‖x‖+‖y‖≧‖x+y‖に拡張した時(すなわち整数線に垂直する高さの概念を認め、面積の概念が生じる時)初めて距離/計量関数(Distance/Metric Function)操作が統計学上の順位尺度の概念にまで影響を与える展開を迎える(計算の都合上、五問それぞれに20点が割り振られた百点満点のテストの得点配分を「10点/15点/15点/30点/30点」と割り振り直して再集計する場合などに対応?)。この時点ではまだ座標軸{x,y}に立脚するデカルト座標系(Cartesian Coordinate System)そのものが完全成立する訳ではない点に注意。
【初心者向け】方形描画関数②距離空間との関係。
-
実数列と言いながら原則として扱うのは整数で、群論でいう加法整数群(Additive Integer Group)に近い概念です。実際に比較してみると10進法概念導入済みである為、小数点下も扱える事(少数点を含む積が現れても集合の要素と見做すが、その時はそもそも「半径1の単位円」に対応する1の概念そのものが動いたと見做し、集合全体の桁調整が遂行される。コンピューター上における不動小数点の概念の援用?)、2を公比(Common Ratio)とする等比数列(Geometric Sequence=幾何数列)2n(n=-Inf→0→Inf)={…(2×n)^(n-1)…}={1/(2^Inf):=0,…,1/2^2=1/4,1/2,2/2=1,2,2^2=4,…,2^Inf=Inf}に従って分割/合成が可能ながら、そうした演算全てに偶奇概念がついて回る辺りが異なります。こうして同じ実数集合(Real Set)を共有する群が複数になったので以降、これを場合によっては実数族(Real Famiry)とも呼ぶ事にしましょう。
【初心者向け】群論概念①基本定義


要するに「半径の2倍は直径⇄直径の半分は半径」なる概念を群規定して一般化したかったのです。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
- 「偶奇性の発生」ばかりか「ピタゴラスの定理(Pythagorean Theorem)y=±sqrt(1-x^2)が半円しか描けない問題」「緯度経度法において緯度が経度の、三次元極座標系において垂直角θが水平角φの半分で済む問題」「複素数に共役性が存在する問題」全てがこの段階での「無限遠点Infinityの±方向への分割」に関係してくる。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?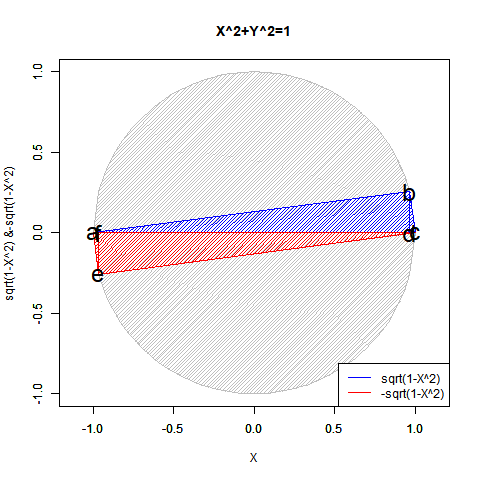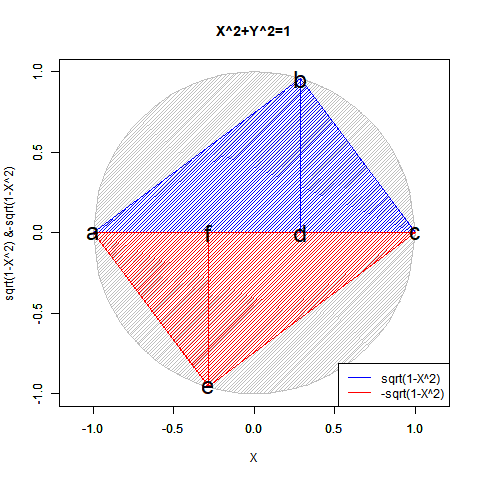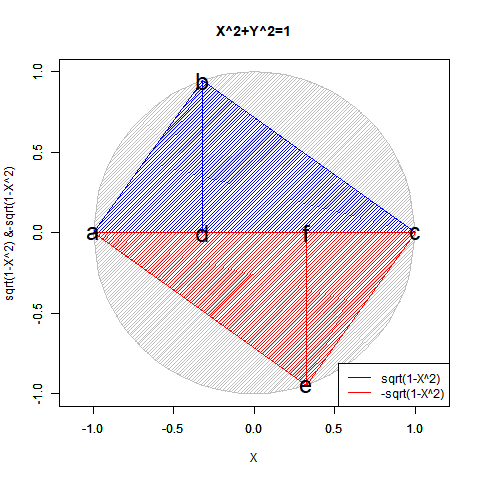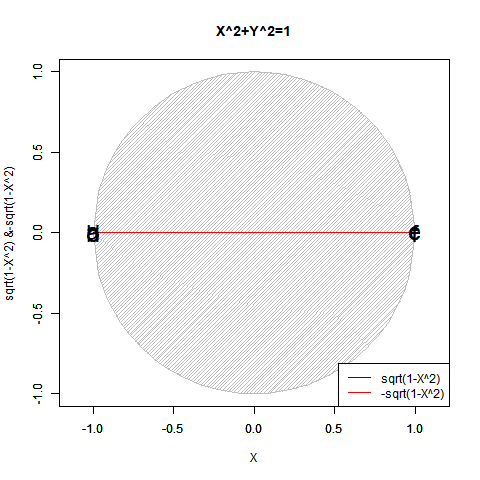
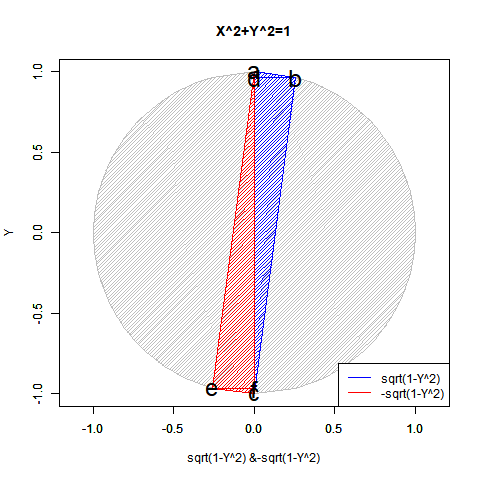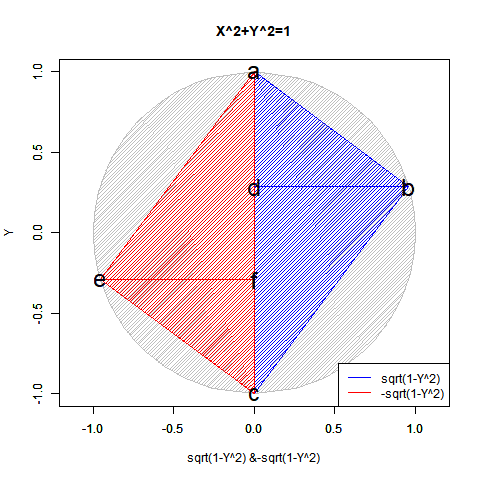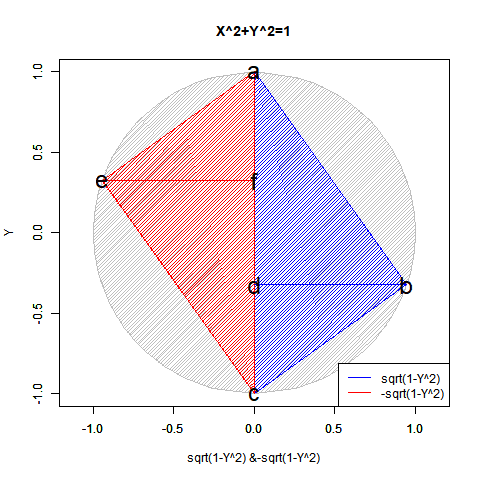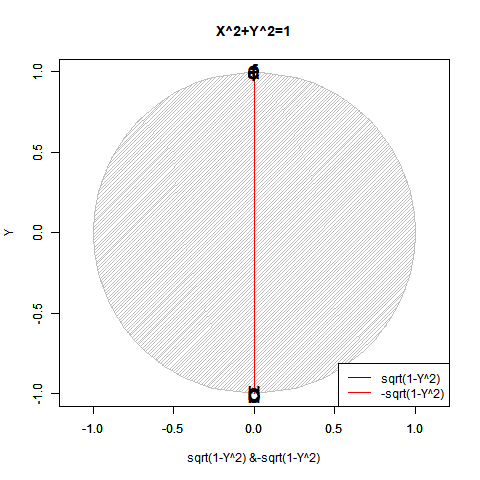
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
【初心者向け】複素共役(Complex Conjugate)のアニメーション表示について。
この棒型タワシの様な空間は、付帯する虚数次元も併せて考えると線形条件|x+y|=|x|+|y|が破れています(1.5次元)。その様な空間として他にフーリエ変換の演算領域があり、実際この空間も同様にその計算対象区画を演算条件に合わせて指定区域内(定積分の概念に対応する有限範囲)、周期1の無限反復(単位トーラスの概念に対応)、(無限小-Infから無限大Infの範囲を扱う)繰り返しなき無限範囲(広義積分の概念に対応。無限遠で無限大と無限小が連なる無限大トーラス構造とも見做せる)と切り替えて考える事が出来るのです。そしてフーリエ変換と構造が似ているのだから(実際基底関数定義もかなり重なりそう)、関数列の形に書き換える事も可能かもしれません。
オイラーの公式(Eulerian Formula)はこの空間にどう作用するのか?
上掲の1.0-1.5次元空間には-Inf→0→Infの整数尺と、これを0→1→Infの範囲に射影した対数尺が並存しています。そう、ここで思い出すべきは「乗法群の演算においてはスカラー倍といっても、それが添字単位、周期単位ともに-Inf→0→Infの範囲の均等尺上でなく、それを0→1→Infの範囲に射影した対数尺上で遂行される」ルール…
-
複素指数関数型フーリエ級数展開の演算領域において棒型タワシ状態を担保しているのは多価関数の分岐点(Branch Point)ごとの分枝切断(Branch Cut)が生み出す螺旋構造、すなわちリーマン面(Riemann Surface)の形成である。
複素解析での分岐点とは
これに関してオイラーの公式exp(xi)は一体どういう作用をもたらすのでしょうか? とりあえず分かっている事を列記してみます。
- -Inf→0→Infの範囲の均等尺を0→1→Infの範囲の対数尺に射影すると、虚軸2の座標がexp(1)(2.718282)、虚軸-1の座標がexp(-1)(0.3678794)へと限りなく近づく。
- 複素自然指数関数exp(xi)は添字として与えられた複素数iの実軸と虚軸双方に影響を与える。その結果、π×(0+1i)の座標は(2,0),π×(0-1i)の座標は(-2,0)に限りなく近付き、途中座標はそれぞれ(1,0)(-1,0)に対して均等な距離を保った円を描く(オイラーの等式)。
- Cos波はこの座標変換を実軸側から観測した場合のexp(1)とexp(-1)の平均、Sin波はこの座標変換を虚軸から観測した場合のexp(1)とexp(-1)の平均に他ならない。
Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)
}
# グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
# 背景描画
c00<-seq(-pi,pi,length=61)
c01<-exp(c00*(0+1i))
plot(c01+(0+1i),type="l",asp=1,xlim=c(-pi,pi),ylim=c(0,pi),main="Even Scale to Logarithmic Scale",xlab="Real",ylab="Imaginal")
par(new=T)
plot(c01+1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(0,pi),main="",xlab="",ylab="")
par(new=T)
plot(c01-1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(0,pi),main="",xlab="",ylab="")
par(new=T) # 上書き指定
plot(-Re(ei01)+1,Im(ei01),asp=1,xlim=c(-pi,pi),ylim=c(0,pi),type="l",main="", xlab="", ylab="",col=rgb(0,0,1))
par(new=T) # 上書き指定
plot(-Re(-ei02)-1,-Im(ei02),asp=1,xlim=c(-pi,pi),ylim=c(0,pi),type="l",main="", xlab="", ylab="",col=rgb(1,0,0))
segments(-2,0,2,0)
abline(h=(1+3/n)^n,col=c(200,200,200))
abline(h=(1+2.5/n)^n,col=c(200,200,200))
abline(h=(1+2/n)^n,col=c(200,200,200))
abline(h=(1+1.5/n)^n,col=c(200,200,200))
abline(h=(1+1/n)^n,col=rgb(0,1,0))
abline(h=(1+0.5/n)^n,,col=c(200,200,200))
abline(h=1,col=c(200,200,200))
abline(h=(1-0.5/n)^n,,col=c(200,200,200))
abline(h=(1-1/n)^n,col=rgb(0,1,0))
abline(h=(1-1.5/n)^n,col=c(200,200,200))
abline(h=(1-2/n)^n,col=c(200,200,200))
abline(h=(1-2.5/n)^n,col=c(200,200,200))
abline(h=(1-3/n)^n,col=c(200,200,200))
Text<-paste("(1±1/",n,")^",n,"=",round((1+1/n)^n,digits=4),"/",round((1-1/n)^n,digits=4))
legend("topleft", legend=c("π×(0+1i)","π×(0-1i)",Text), lty=c(1,1,1), col=c(rgb(0,0,1),rgb(1,0,0),rgb(0,1,0)))
}
# アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
分かった様なわからない様な…いずれにせよこの座標変換を縦軸、すなわち(極座標系で表される)半径1の単位円とこれを原点とする(自然指数関数により0からInfの間の値として表される)リーマン面の添字集合に適用すると現れるのがリーマン球面(Riemann sphere)となる様です。
リーマン球面 - Wikipedia
【初心者向け】「単位円筒」から「単位球面」へ

これも数直線が無限遠点Infを無限小-Infと無限大Infに分割した影響の一つ? ああ、今度はメビウス変換(Möbius Transformation)が怖い…
メビウス変換 - Wikipedia
一次分数変換(メビウス変換)と円円対応
詳しい解説は以下続報…






