推計統計学(inferential statistics)を展開する上での前提環境。
- 代表値(Representative value)としては平均(Mean)、中央値(Median)、最頻値(Mode)の概念を用いる。
- 散布度合いの基準としては範囲(Range)や標本分散(Sample Dispersion)/不偏分散(Unbiased Dispersion)の概念を用いる。
- 分散度合いの基準としては標準偏差(Standard Deviation)や平均偏差(Mean Deviation)の概念を用いる。
- 複数のデータセットの関連度については共分散(Covariance)や相関係数(Correlation Coefficient)の概念を用いる。
統計言語Rには処理のほとんどが標準関数の形で実装されています。
基本的諸元の世界
統計言語RだとSummary関数がまとめて表示してくれる範囲。要するにこの単位で俯瞰する事に相応の意義があるという事。
> df <- data.frame(sample_data = rnorm(n = 100, mean = 0, sd = 1))
# 標準分布では中央値と平均値がそう大きくは変わらない。
> summary(df)
sample_data
Min. :-3.3485
1st Qu.:-0.8626
Median :-0.1940
Mean :-0.1937
3rd Qu.: 0.4787
Max. : 2.0784
>
①クォンタイル/四分位(Quantile)…「最小値(Min)・第1四分位(1st Quartile)・中央値(Median)・第3四分位(3rd Quartile)・最大値(Max)」で構成される目安。
- 最小値(Min)…散布度基準の一つである範囲(Range)の構成要素。
- 最大値(Max)…同じく散布度基準の一つである範囲(Range)の構成要素。
-
中央値(Median)…分布の中心にあるデータの数値。候補データが複数存在する場合にはその平均。年収リストの様な中央値と平均が異なる分布では、概ね中央値の方が平均値を下回る。平均値(Mean)と異なり、外れ値の影響に対してロバスト(頑強)とされる。
【初心者向け】平均と標準偏差、中央値と平均偏差
②平均値(Mean)…データの各数値の和をデータ数で割ったもの。偏差(Deviation)などの算出に使われる。正規分布に与えるパラメーターの一つ(確率辺数分布の頂点を左右に動かす)。外れ値の影響を受ける。
【初心者向け】平均と標準偏差、中央値と平均偏差
> sample_data<-c(300,300,300,300,400,400,400,2000,9000)
> summary(sample_data)
Min. 1st Qu. Median Mean 3rd Qu. Max.
300 300 400 1489 400 9000
# クォンタイル(Quantile)
> quantile(sample_data)
0% 25% 50% 75% 100%
300 300 400 400 9000
# 最小値(Min)
> min(sample_data)
[1] 300
# 最大値(Max)
> max(sample_data)
[1] 9000
# 中央値(Median)
> median(sample_data)
[1] 400
# 平均値(Mean)
> mean(sample_data)
[1] 1488.889
# 「データの各数値の和をデータ数で割る計算」と結果が一致。
> sum(sample_data)/length(sample_data)
[1] 1488.889
中央値(Median)は平均値(Mean)ほど外れ値の影響を受けない事の検証。
# 元データ
> sample_data01<-c(300,300,300,300,400,400,400,2000,9000)
> median(sample_data01)
[1] 400
> mean(sample_data01)
[1] 1488.889
# 外れ値の値を大きくしてみる。
> sample_data02<-c(300,300,300,300,400,400,400,2000,12000)
> median(sample_data02)
[1] 400
> mean(sample_data02)
[1] 1822.222
度数分布表(Histogram)と縁深い範囲(Range)と最頻値(Mode)の世界
度数分布表(Histogram)は、連続分布においてはしばしばその作成過程そのものが「データ分布の(確率密度に対応した)クラス分けの最適化」なる分析過程を伴います。
【初心者向け】度数分布と最頻値
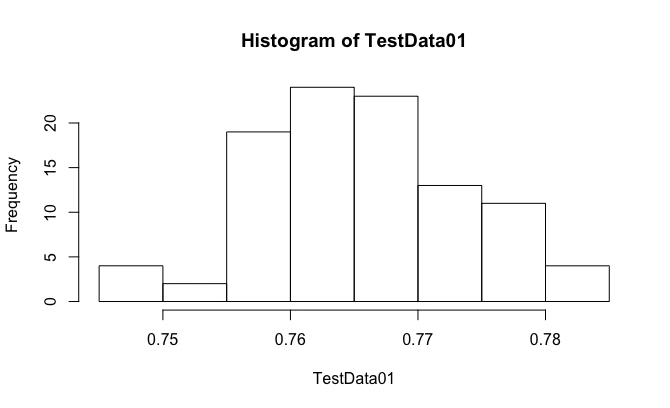
- 範囲(Range)…散布度基準の一つだが、あまり普及してない。最大値(Max)-最小値(Min)。度数分布(Frequency Distribution)の表現形態の一つたるヒストグラム(Histogram)では「階級(Class)の最大値-階級(Class)の最小値」と計算される。
- 最頻値(Mode)…日本工業規格の定義では「離散分布の場合は確率関数が,連続分布の場合は密度関数が最大となる確率変数の値。分布が多峰性の場合は,それぞれの極大値を与える確率変数の値」と定めている。
> sample_data<-c(300,300,300,300,400,400,400,2000,9000)
# 範囲(Range)
> range(sample_data)
[1] 300 9000
# 最頻値(Mode)。標準関数の形では実装されてない。
# そこでまずtable関数を使ってまず出現頻度を確かめる。
> table(sample_data)
sample_data
300 400 2000 9000
4 3 1 1
# 次いでwhich.max()関数で最頻値が頻度表の何番目にあるか確認。
# names関数で取り出す。
> names(which.max(table(sample_data)))
[1] "300"
# あるいはtable関数で取り出した頻度表をソートして
# 逆転し第1項を取り出す。
> names(rev(sort(table(sample_data))))[1]
[1] "300"
最頻度の求め方は豊田秀樹「共分散構造分析R編」より。
R言語における最頻値の求め方
そして連続分布の度数分布表示では、いよいよ「クラス分け」が必須に。
> sample_data<-rnorm(n=100,mean=0,sd=1)
> range(sample_data)
[1] -2.053325 2.919551
# 度数分布表の区間指定
> breaks <- seq(-3,3,1)
> table(cut(sample_data, breaks))
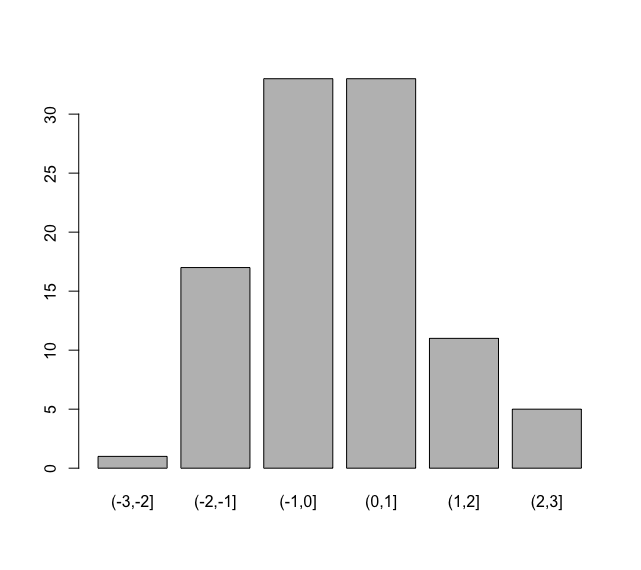
(-3,-2] (-2,-1] (-1,0] (0,1] (1,2] (2,3]
1 17 33 33 11 5
このデータを利用して、そのままヒストグラムが描画可能です。
result<-table(cut(sample_data, breaks))
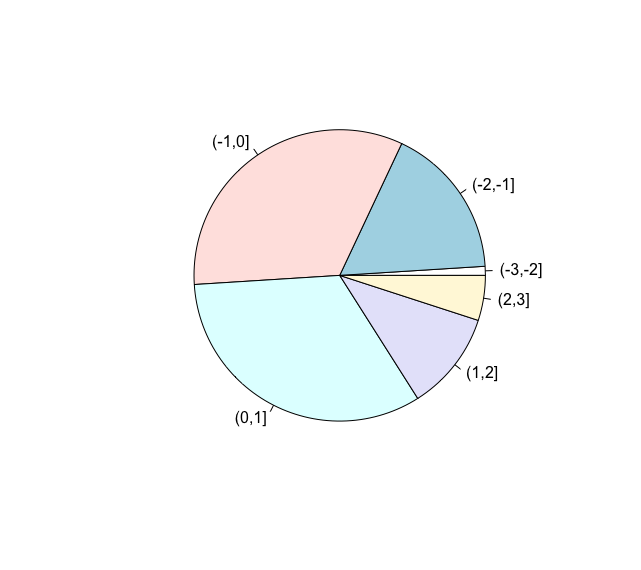
barplot(result)
pie(result)
また、この系列の確率分布はサンプル数が増大するにつれ「大数の弱法則 (WLLN: Weak Law of Large Numbers) 」や「中心極限定理(CLT=Central Limit Theorem)」の影響を大きく受ける様になっていきます。サンプル数が一定以下だとそれぞれが特徴ある多様性や多態性を示す分布の多くが、その結果、正規分布(Normal Distribution)へと収束していくのであり、その意味合いにおいては正規分布もまた無限遠点(Inf(inity))の一種といえそうです。
【初心者向け】正規分布(Normal Distribution)とは何か?


偏差(Deviation)概念から出発する分散(Dispersion)と偏差値(Deviation Value)、そして相関係数(Correlation Coefficient)の確認を経て単回帰分析(Simple Regression Analysis)の世界へ。
ここでは偏差(Deviation)、すなわち「データの各数値より、その平均を引いた残り」の算出が出発点となります。定数項を除いて分布の中心を原点に戻す操作。
基本統計量の算出- R-Source
# まず10人の患者から成る2グループx,yにそれぞれ異なる睡眠薬を飲ませ,
# 睡眠時間の増加を示すデータを準備する。
x <- c(0.7,-1.6,-0.2,-1.2,-0.1,3.4,3.7,0.8,0.0,2.0)
y <- c(1.9, 0.8, 1.1, 0.1,-0.1,4.4,5.5,1.6,4.6,3.4)
# xの平均(Mean)
> mean(x)
[1] 0.75
# xの偏差(Deviation)
> x-mean(x)
[1] -0.05 -2.35 -0.95 -1.95 -0.85 2.65 2.95 0.05 -0.75 1.25
# yの平均(Mean)
> mean(y)
[1] 2.33
# yの偏差(Deviation)
> y-mean(y)
[1] -0.43 -1.53 -1.23 -2.23 -2.43 2.07 3.17 -0.73 2.27 1.07
①標本分散(Sample Dispersion)と不偏分散(Unbiased Dispersion)
- 標本分散(Sample Dispersion)…偏差^2の合計/標本数
- 不偏分散(Unbiased Dispersion)…偏差^2の合計/(標本数-1)
# 不偏分散(Unbiased Dispersion)
> var(x)
[1] 3.200556
> sum((x-mean(x))^2)/(length(x)-1)
[1] 3.200556
# 標本分散(Sample Dispersion)
> var(x)*(length(x)-1)/length(x)
[1] 2.8805
# 標本分散自体を求める関数は存在しないので工夫
> sum((x-mean(x))^2)/length(x)
[1] 2.8805
散布度基準の一つ。状況によって使い分けるのが正しいが、結果として不偏分散の概念が広まった。
【初心者向け】標本分散と不偏分散
②標準偏差(Standard Deviation)と平均偏差(Mean Deviation)
- 標準偏差(Standard Dispersion)…分散の平方根
- 平均偏差(Mean Deviation)…偏差の絶対値の平均
# 標準不偏偏差(Standard Unbiased Dispersion)
> sd(x)
[1] 1.78901
> sqrt(var(x))
[1] 1.78901
# 標準標本偏差(Standard Sample Dispersion)
> sqrt(var(x)*(length(x)-1)/length(x))
[1] 1.697204
> sqrt(sum((x-mean(x))^2)/length(x))
[1] 1.697204
# 平均偏差(Mean Deviation)…偏差の絶対値の平均
> sum(abs(x-mean(x)))/length(x)
[1] 1.38
標準偏差は平均(Mean)、平均偏差は中央値(Median)を代表値とする。
【初心者向け】平均と標準偏差、中央値と平均偏差
③Z得点(Z Value)と偏差値(Deviation Value)
- Z得点(Z Value)…偏差/標準偏差
- 偏差値(Deviation Value)…Z得点*10+50
# Z得点(Z Value)
> (x-mean(x))/sd(x)
[1] -0.02794842 -1.31357592 -0.53102005 -1.08998853 -0.47512320 1.48126646 1.64895700
[8] 0.02794842 -0.41922636 0.69871059
# 偏差値(Deviation Value)
> (x-mean(x))/sd(x)*10+50
[1] 49.72052 36.86424 44.68980 39.10011 45.24877 64.81266 66.48957 50.27948 45.80774
[10] 56.98711
分散度合いをさらに標準化。言葉としての「偏差値」が20世紀の受験戦争以降一般にも定着したが、その過程で内容についての誤解も広がった。
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史
④共分散(Covariance)と相関係数(Correlation Coefficient)
- 共分散(Covariance)…平均からの偏差の積の平均値
- 相関係数(Correlation Coefficient)…共分散の値を、各変数の標準偏差の積で割ったもの
# 不偏共分散(Unbiased Covariance)
> var(x, y)
[1] 2.848333
# 標本共分散(Sample Covariance)
> var(x,y)*(length(x)-1)/length(x)
[1] 2.5635>
# 相関係数(Correlation Coefficient)
> cor(x,y)
[1] 0.7951702
ところで最終的に標本相関係数(Sample Correlation Coefficient)と不偏相関係数(Unbiased Correlation Coefficient)の結果は一致する。
相関係数の意味と求め方 - 公式と計算例
相関係数を求めるには、共分散をそれぞれの変数の標準偏差で割ります。
具体的には次の6つのステップで求めます。①それぞれの変数の平均値を求める。
②それぞれの変数の偏差(数値-平均値)を求める。
③それぞれの変数の分散(偏差の二乗平均)を求める。
④それぞれの変数の標準偏差(分散の正の平方根)を求める。
⑤共分散(偏差の積の平均)を求める。
⑥共分散を2つの変数の標準偏差で割って相関係数を得る。
ここに例示されている以下のデータをコンピューターに解かせる。
# A~Eさんの英語(x)と数学(y)のテスト結果。
x<-c(50,60,70,80,90)
y<-c(40,70,90,60,100)
①それぞれの変数の平均値を求める。
> x_mean<-mean(x)
> x_mean
[1] 70
> y_mean<-mean(y)
> y_mean
[1] 72
②それぞれの変数の偏差(数値-平均値)を求める。
x_deviation<-x-x_mean
x_deviation
y_deviation<-y-y_mean
y_deviation
> x_deviation<-x-x_mean
> x_deviation
[1] -20 -10 0 10 20
> y_deviation<-y-y_mean
> y_deviation
[1] -32 -2 18 -12 28
③それぞれの変数の分散(偏差の二乗平均)を求める。
# 標本分散(Sample Covariance)。
> var(x)*(length(x)-1)/length(x)
[1] 200
> x_dispersion<-sum(x_deviation^2)/length(x)
> x_dispersion
[1] 200
> var(y)*(length(y)-1)/length(y)
[1] 456
> y_dispersion<-sum(y_deviation^2)/length(y)
> y_dispersion
[1] 456
# 不偏分散(Unbiased Dispersion)とのズレ。
> var(x)
[1] 250
> var(y)
[1] 570
④それぞれの変数の標準偏差(分散の正の平方根)を求める。
# 標準標本偏差(Standard Sample Dispersion)。
> x_Standard_Dispersion<-sqrt(x_dispersion)
> x_Standard_Dispersion
[1] 14.14214
> y_Standard_Dispersion<-sqrt(y_dispersion)
> y_Standard_Dispersion
[1] 21.35416
# 標準不偏偏差(Standard Unbiased Dispersion)とのズレ。
> sd(x)
[1] 15.81139
> sd(y)
[1] 23.87467
⑤共分散(偏差の積の平均)を求める。
# 標本共分散(Sample Covariance)
> var(x,y)*(length(x)-1)/length(x)
[1] 220
> x_deviation*y_deviation
[1] 640 20 0 -120 560
> xy_covariance<-sum(x_deviation*y_deviation)/length(x)
> xy_covariance
[1] 220
# 不偏共分散(Unbiased Covariance)とのズレ。
> var(x, y)
[1] 275
⑥共分散を2つの変数の標準偏差で割って相関係数を得る。
# 最終的に標本相関係数と不偏相関係数は一致する。
# 標本相関係数(Sample Correlation Coefficient)
> xy_covariance/(x_Standard_Dispersion*y_Standard_Dispersion)
[1] 0.7284928
# 不偏相関係数(Unbiased Correlation Coefficient)
> cor(x,y)
[1] 0.7284928
相関係数は−1から1までの値をとり、1であれば2つの変数の値は完全に同期している事になる。対象によって相関係数の意味はかなり変わってくるが、一般的見方は以下。
- −1〜−0.7…強い負の相関
- −0.7〜−0.4…かなりの負の相関
- −0.4〜−0.2…やや負の相関
- −0.2〜0.2…ほとんど相関なし
- 0.2〜0.4…やや正の相関
- 0.4〜0.7…かなりの正の相関
- 0.7〜1…強い正の相関
このデータでは「強い正の相関」が検出されたので、さらに最小二乗法(Least Squares Method)による単回帰分析(Simple Regression Analysis)へと進む。
# 引き渡すデータの生成
> xy_data <- data.frame(X=x, Y=y)
# 回帰分析を行う
> result <- lm(X ~ Y, data = xy_data)
# 結果表示
> result
Call:
lm(formula = X ~ Y, data = xy_data)
Coefficients:
(Intercept) Y
35.2632 0.4825
# 分析結果の要約
> summary(result)
Call:
lm(formula = X ~ Y, data = xy_data)
Residuals:
1 2 3 4 5
-4.561 -9.035 -8.684 15.789 6.491
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.2632 19.6714 1.793 0.171
Y 0.4825 0.2619 1.842 0.163
Residual standard error: 12.51 on 3 degrees of freedom
Multiple R-squared: 0.5307, Adjusted R-squared: 0.3743
F-statistic: 3.393 on 1 and 3 DF, p-value: 0.1627
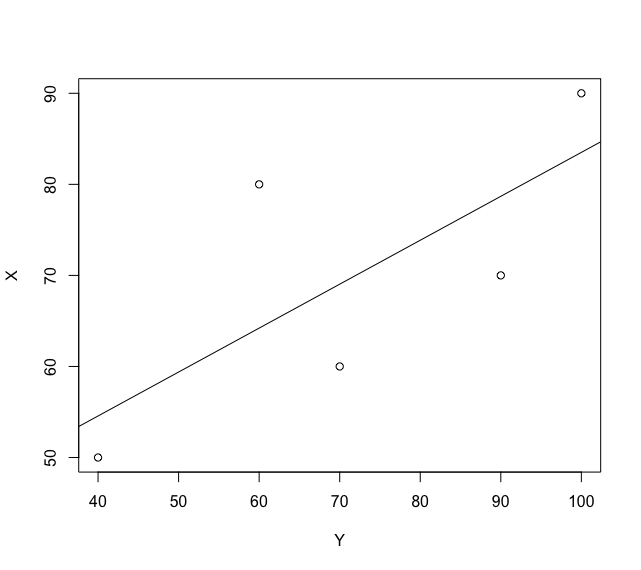
# グラフ表示
> plot(X ~ Y, data = xy_data) # 散布図を描く
> abline(result) # 推定回帰直線を描く
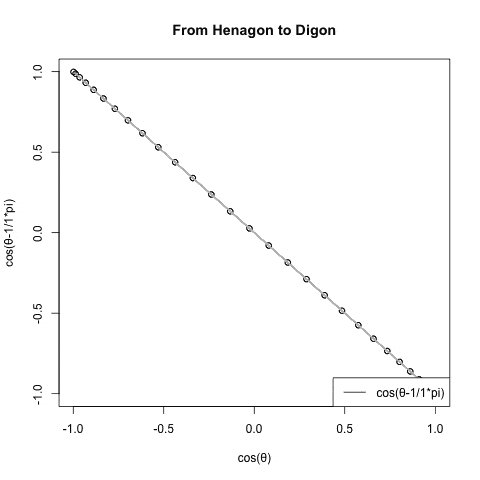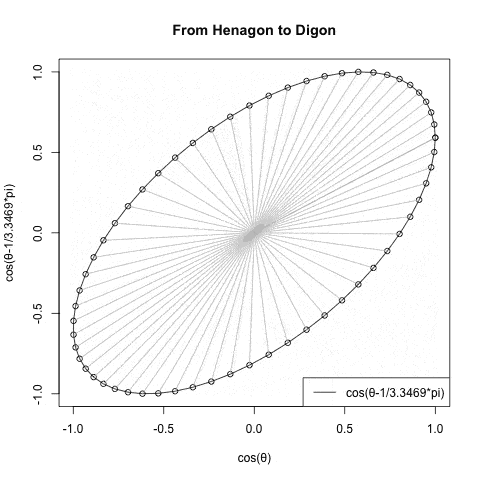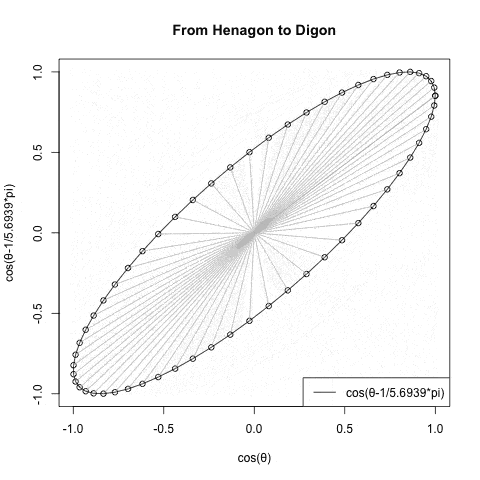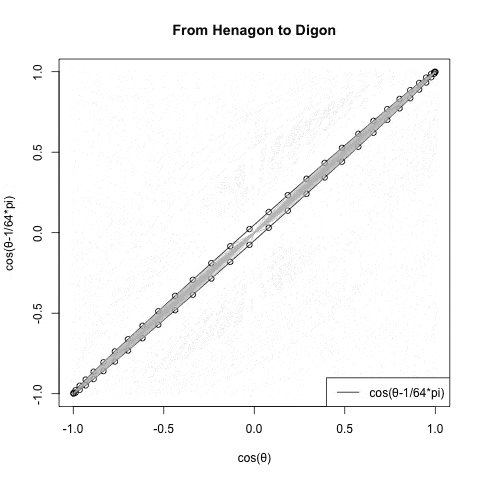
なお相関係数の概念は直線{-1,0,1}の形ではなく傾きに応じて両極で直線に収束する(無相関の時に真円となる)楕円の推移でイメージする。
【Rで球面幾何学】二辺形(Bilateral)と一辺形(One Side)?
# 複素平面(球面)
Complex_plane<-function(x){
ifelse*2
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_cos<-cos(theta01)
plot(cos(theta), sin(theta), xlim=c(-1,1), ylim=c(-1,1), type="l", main="Correlation coefficient",xlab="Real Expanse", ylab="Imaginal Expanse")
par(new=T)#上書き指定
plot(theta_cos,theta00,xlim=c(-1,1), ylim=c(-1,1), type="l",col=rgb(0,1,0),main="",xlab="", ylab="")
# cos(x)を塗りつぶす
polygon(theta_cos, #x
theta00, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
# 線を引く
segments(cos(dr[x]),sin(dr[x]),0,0,col=segC)
# 内積を塗りつぶす
polygon(c(cos(dr[x]),cos(dr[x]),0), #x
c(sin(dr[x]),0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=segC) #塗りつぶす色
legend("bottomleft", legend=c("cos", "inner product"), lty=c(1,1),col =c(rgb(0,1,0),segC))
}
# アニメーションさせてみる。
library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
そんな感じで以下続報…