物理学の世界(The Set of Physical Things)においては、概ね「Sin(θ)関数とCos(θ)関数は等速円運動(Constant Velocity Circular Motion)のX軸方向からとY軸方向からの観測結果(Observation Results)から得られる」なる簡潔極まりない説明があるだけです。
【初心者向け】物理学における「単位円筒」の概念について。



ここから自明の場合(Trival Case)として(円描画に要する時間をZ軸に配した)単位円筒(Unit Cylinder)の概念が派生してくる訳です。誰かの証明を待つまでもなく、かつまた疑問を挟む余地もない完璧な記述…

XY軸(円弧)
ZX軸(Cos波)
ZY軸(Sin波)
一体誰でしょう、この方便を科学史上初めて思いついた偉大なる物理学者は…
方便 - Wikipedia
そして数学の世界(The Set of Mathematical Things)においてはこの問題、一体どう語られているのでしょうか? 今回はあえて搦手、すなわち方形描画関数(Square Drawing Function)の世界から話を始めたいと思います。
方形描画関数Cos(θ)±(1-abs(Cos(θ)))i
そもそもCos(θ)関数の正体は直径{-1,0,1}(距離2)における右端(1)→中央(0)→左端(-1)→中央(0)→右端(1)の往復。それぞれの区画を等差数列風表現(Arithmetic Sequence Style Expression)に分解すると1辺がsqrt(2)の正方形が現れます。案外面倒なのが三角関数表現(Trigonometric Function Expression)に対応させる為の「増減の向き合わせ」だったりします。
-
右端(1)→中央(0)…等差数列風表現における定義「初項(First Term)0,交差(Common Defference)1」を逆転させた場合。
三角関数表現では1-cos(0→π/2)=sin(0→π/2)と表される。 -
中央(0)→左端(-1)…等差数列風表現における定義「初項(First Term)1,交差(Common Defference)-1」を逆転させた場合。
三角関数表現では1+cos(π/2→π)=sin(π/2→π)と表される。 -
左端(-1)→中央(0)…等差数列風表現における定義「初項(First Term)0,交差(Common Defference)-1」に該当。
三角関数表現では-(1+cos(π→3π/2))=sin(π→3π/2)と表される。 -
中央(0)→右端(1)…等差数列風表現における定義「初項(First Term)-1,交差(Common Defference)1」に該当。
三角関数表現では-(1-cos(3π/2→2π))=sin(3π/2→2π)と表される。

Cos00<-function(Radian){
c0<-seq(0,pi*2,length=61)
cx<-cos(c0)
cy=c(1-cos(c0[1:15]),1+cos(c0[16:30]),-(1+cos(c0[31:45])),-(1-cos(c0[46:61])))
plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Cos(θ)±(1±cos(θ))i",xlab="x=Cos(θ)",ylab="y=±(1±cos(θ))i")
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
# θ位置を書き添える 。
text(cx[Radian],cy[Radian],"θ",col=rgb(0,1,0))
segments(0,0,cx[Radian],cy[Radian],col=rgb(0,1,0))
# 凡例を書き添える 。
legend("topright", legend=c("y=Cos(θ)±(1±cos(θ))i","x=y=0","x=Cos(θ)"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,1,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Cos00(i)
}
}, interval = 0.1, movie.name = "Cos05.gif")
この関数はCos(θ)±(1-abs(Cos(θ)))iの形に整理出来ます。グラフの形は全くの同一。
- 右端(1)→中央(0)→左端(-1)…三角関数で1-cos(0→π)=sin(0→π)と表せる。
- 左端(-1)→中央(0)→右端(1)…三角関数で-(1-cos(π→2π))=sin(π→2π)と表せる。
Cos01<-function(Radian){
c0<-seq(0,pi*2,length=61)
cx<-cos(c0)
cy=c((1-abs(cos(c0[1:30]))),-(1-abs(cos(c0[31:61]))))
plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Cos(θ)±(1-abs(Cos(θ)))i",xlab="x=Cos(θ)",ylab="y=±(1-abs(±Cos(θ)))i")
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
# θ位置を書き添える 。
text(cx[Radian],cy[Radian],"θ",col=rgb(0,1,0))
segments(0,0,cx[Radian],cy[Radian],col=rgb(0,1,0))
# 凡例を書き添える 。
legend("topright", legend=c("y=Cos(θ)±(1-abs(Cos(θ)))i","x=y=0","x=Cos(θ)"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,1,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Cos01(i)
}
}, interval = 0.1, movie.name = "Cos09.gif")
方形描画関数Sin(θ)±(1-abs(Sin(θ)))i
同じくSin(θ)関数の正体は直径{-1,0,1}(距離2)を中央(0)→右端(1)→中央(0)→左端(-1)→中央(0)の往復。それぞれの区画を等差数列風表現に分解すると同じく1辺がsqrt(2)の正方形が現れます。θの回転方向が逆になるの点に注意。
-
中央(0)→右端(1)…等差数列風表現における定義「初項(First Term)1,交差(Common Defference)-1」に該当。
三角関数表現では1-sin(0→π/2)=cos(0→π/2)と表される。 -
右端(1)→中央(0)…等差数列風表現における定義「初項(First Term)1,交差(Common Defference)-1」を逆転させた場合。
三角関数表現では-(1-sin(π/2→π))=cos(π/2→π)と表される。 -
中央(0)→左端(-1)…等差数列風表現における定義「初項(First Term)-1,交差(Common Defference)1」を逆転させた場合。
三角関数表現では-(1+sin(π→3π/2))=cos(π→3π/2)と表される。 -
左端(-1)→中央(0)…等差数列風表現における定義「初項(First Term)0,交差(Common Defference)1」を逆転させた場合。
三角関数表現では1+sin(3π/2→2π)=cos(3π/2→2π)と表される。
Sin00<-function(Radian){
c0<-seq(0,pi*2,length=61)
cx<-sin(c0)
cy=c(1-sin(c0[1:15]),-(1-sin(c0[16:30])),-(1+sin(c0[31:45])),1+sin(c0[46:61]))
plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Sin(θ)±(1±sin(θ))i",xlab="x=Sin(θ)",ylab="y=±(1±sin(θ))i")
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
# θ位置を書き添える 。
text(cx[Radian],cy[Radian],"θ",col=rgb(0,1,0))
segments(0,0,cx[Radian],cy[Radian],col=rgb(0,1,0))
# 凡例を書き添える 。
legend("topright", legend=c("y=Sin(θ)±(1±sin(θ))i","x=y=0","x=Sin(θ)"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,1,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Sin00(i)
}
}, interval = 0.1, movie.name = "Sin12.gif")
この関数もSin(θ)±(1-abs(Sin(θ)))iの形に整理出来ます。こちらもグラフの形自体は合一。
- 中央(0)→右端(1)→中央(0)…三角関数により1-abs(sin(π/2→-π/2))=cos(π/2→-π/2)と表せる。
- 中央(0)→左端(-1)→中央(0)…三角関数により-(1-abs(-π/2→π/2)))=cos(-π/2→π/2)と表せる。
Sin01<-function(Radian){
c0<-seq(0,pi*2,length=61)
cx<-sin(c0)
cy=c((1-abs(sin(c0[1:15]))),-(1-abs(sin(c0[16:45]))),(1-abs(sin(c0[46:61]))))
plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Sin(θ)±(1-abs(sin(θ)))i",xlab="x=Sin(θ)",ylab="y=±(1-abs(sin(θ)))i")
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
# θ位置を書き添える 。
text(cx[Radian],cy[Radian],"θ",col=rgb(0,1,0))
segments(0,0,cx[Radian],cy[Radian],col=rgb(0,1,0))
# 凡例を書き添える 。
legend("topright", legend=c("y=Sin(θ)±(1-abs(sin(θ)))i","x=y=0","x=Sin(θ)"), lty =c(1,1,1),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,1,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Sin01(i)
}
}, interval = 0.1, movie.name = "Sin01.gif")
直径D{半径-R→0→半径R}上における半径R分のズレ。
つまり
- Cos(θ)=±(1-abs(sin(θ))
- Sin(θ)=±(1-abs(cos(θ))
cos(θ)とsin(θ)の数列の位相がπ/2Rad(ラジアン,90度)だけズレている事が、この関数では半径R分のズレとして現れてくる訳です。
c0<-seq(0,pi*2,length=61)
# cos(θ)=±(1-abs(sin(θ))
> round(sin(c0),digits=4)
[1] 0.0000 0.1045 0.2079 0.3090 0.4067 0.5000 0.5878 0.6691 0.7431 0.8090
[11] 0.8660 0.9135 0.9511 0.9781 0.9945 1.0000 0.9945 0.9781 0.9511 0.9135
[21] 0.8660 0.8090 0.7431 0.6691 0.5878 0.5000 0.4067 0.3090 0.2079 0.1045
[31] 0.0000 -0.1045 -0.2079 -0.3090 -0.4067 -0.5000 -0.5878 -0.6691 -0.7431 -0.8090
[41] -0.8660 -0.9135 -0.9511 -0.9781 -0.9945 -1.0000 -0.9945 -0.9781 -0.9511 -0.9135
[51] -0.8660 -0.8090 -0.7431 -0.6691 -0.5878 -0.5000 -0.4067 -0.3090 -0.2079 -0.1045
[61] 0.0000
> round(c((1-abs(cos(c0[1:30]))),-(1-abs(cos(c0[31:61])))),digits=4)
[1] 0.0000 0.0055 0.0219 0.0489 0.0865 0.1340 0.1910 0.2569 0.3309 0.4122
[11] 0.5000 0.5933 0.6910 0.7921 0.8955 1.0000 0.8955 0.7921 0.6910 0.5933
[21] 0.5000 0.4122 0.3309 0.2569 0.1910 0.1340 0.0865 0.0489 0.0219 0.0055
[31] 0.0000 -0.0055 -0.0219 -0.0489 -0.0865 -0.1340 -0.1910 -0.2569 -0.3309 -0.4122
[41] -0.5000 -0.5933 -0.6910 -0.7921 -0.8955 -1.0000 -0.8955 -0.7921 -0.6910 -0.5933
[51] -0.5000 -0.4122 -0.3309 -0.2569 -0.1910 -0.1340 -0.0865 -0.0489 -0.0219 -0.0055
[61] 0.0000
# Cos(θ)=±(1-abs(sin(θ))
> round(cos(c0),digits=4)
[1] 1.0000 0.9945 0.9781 0.9511 0.9135 0.8660 0.8090 0.7431 0.6691 0.5878
[11] 0.5000 0.4067 0.3090 0.2079 0.1045 0.0000 -0.1045 -0.2079 -0.3090 -0.4067
[21] -0.5000 -0.5878 -0.6691 -0.7431 -0.8090 -0.8660 -0.9135 -0.9511 -0.9781 -0.9945
[31] -1.0000 -0.9945 -0.9781 -0.9511 -0.9135 -0.8660 -0.8090 -0.7431 -0.6691 -0.5878
[41] -0.5000 -0.4067 -0.3090 -0.2079 -0.1045 0.0000 0.1045 0.2079 0.3090 0.4067
[51] 0.5000 0.5878 0.6691 0.7431 0.8090 0.8660 0.9135 0.9511 0.9781 0.9945
[61] 1.0000
> round(c((1-abs(sin(c0[1:15]))),-(1-abs(sin(c0[16:45]))),(1-abs(sin(c0[46:61])))),digits=4)
[1] 1.0000 0.8955 0.7921 0.6910 0.5933 0.5000 0.4122 0.3309 0.2569 0.1910
[11] 0.1340 0.0865 0.0489 0.0219 0.0055 0.0000 -0.0055 -0.0219 -0.0489 -0.0865
[21] -0.1340 -0.1910 -0.2569 -0.3309 -0.4122 -0.5000 -0.5933 -0.6910 -0.7921 -0.8955
[31] -1.0000 -0.8955 -0.7921 -0.6910 -0.5933 -0.5000 -0.4122 -0.3309 -0.2569 -0.1910
[41] -0.1340 -0.0865 -0.0489 -0.0219 -0.0055 0.0000 0.0055 0.0219 0.0489 0.0865
[51] 0.1340 0.1910 0.2569 0.3309 0.4122 0.5000 0.5933 0.6910 0.7921 0.8955
[61] 1.0000
円筒座標系上の「算盤球」を経て正八面体(Regular Octahedron)へ
関数形をCos(θ)±(1-abs(Sin(θ)))iあるいはSin(θ)±(1-abs(Sin(θ)))iなる形に特定出来たので円筒座標系(Cylindrical Coordinate System)への射影が可能となります。誰もが予測する通り二つの円錐の底面を重ねた算盤球の様な図形が得られます。

library(rgl)
f0<-function(x){exp(x*(0+1i))}
# 無限円(Infinity Circle)
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
# 無限球面(Infinity Sphere)
radians<-seq(0,60*pi,length=3000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
# 工夫
f1<-function(x){1-abs(x)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
# > plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1
# 無限球面の描画
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))
# 無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
# 観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)
# 原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")
# 原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)
# 対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")
# 対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)
# 立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)
lines3d(c(0,antipordal_i),c(0,antipordal_j),c(0,antipordal_k),col=rgb(1,0,0),lwd=2)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/soroban01")
もう一方向から射影すると残り1方向からの見え方も自明の場合として定まって正八面体(Regular Octahedron)が現れます。
【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ

それまで素数2^n族のみで構成されてきた構造にいきなり素数3^n族が乱入してくる形で、この辺りの仕組みの解明がこれからの課題という次第。
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…
円筒座標系における発展
それにつけても上掲の等差数列風表現(Arithmetic Sequence Style Expression)とは聞き慣れない表現です。それもその筈。「(実際の全貌がどれほどかけ離れているかに関わらず)象限単位で扱う分にはかろうじてある種の等差数列として扱えない事もない」Cos(θ)関数やSin(θ)関数の特徴を表す為にこの投稿用に拵えたこの場限りの造語に過ぎないんですから。それでは実際にどういう形でかけ離れているかというと…
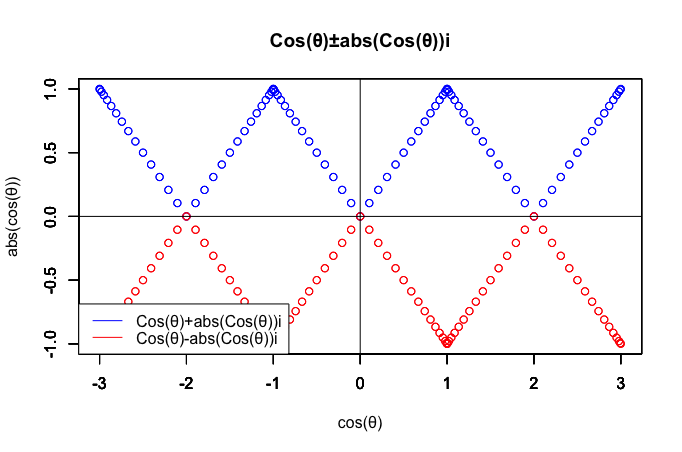
c0<-seq(-pi,pi,length=61)
# cos(θ)+abs(cos(θ))i
plot(cos(c0),abs(cos(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="Cos(θ)±abs(Cos(θ))i",xlab="cos(θ)",ylab="abs(cos(θ))",col=rgb(0,0,1))
par(new=T)
plot(cos(c0)-2,abs(cos(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(cos(c0)+2,abs(cos(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
# cos(θ)-abs(cos(θ))i
plot(cos(c0),-abs(cos(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(cos(c0)-2,-abs(cos(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(cos(c0)+2,-abs(cos(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
abline(v=0)
abline(h=0)
# 凡例を書き添える 。
legend("bottomleft", legend=c("Cos(θ)+abs(Cos(θ))i","Cos(θ)-abs(Cos(θ))i"), lty =c(1,1),col=c(rgb(0,0,1),rgb(1,0,0)))
c0<-seq(-pi,pi,length=61)
# sin(θ)+abs(sin(θ))i
plot(sin(c0),abs(sin(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="Sin(θ)±abs(Sin(θ))i",xlab="Sin(θ)",ylab="abs(Sin(θ))",col=rgb(0,0,1))
par(new=T)
plot(sin(c0)-2,abs(sin(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(sin(c0)+2,abs(sin(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
# sin(θ)-abs(sin(θ))i
plot(sin(c0),-abs(sin(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(sin(c0)-2,-abs(sin(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(sin(c0)+2,-abs(sin(c0)),type="b",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
abline(v=0)
abline(h=0)
# 凡例を書き添える 。
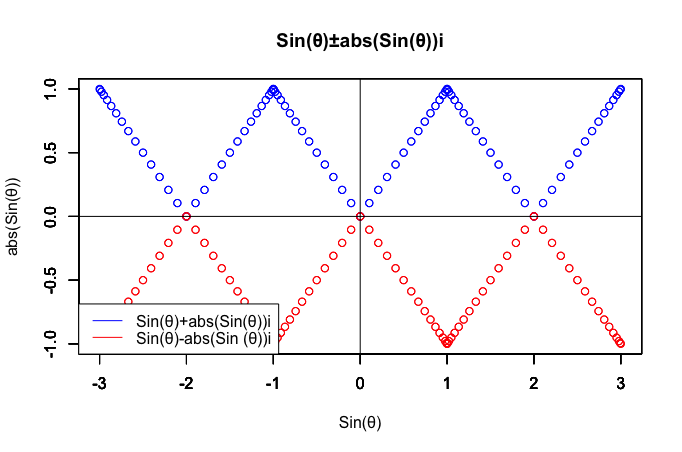
legend("bottomleft", legend=c("Sin(θ)+abs(Sin(θ))i","Sin(θ)-abs(Sin (θ))i"), lty =c(1,1),col=c(rgb(0,0,1),rgb(1,0,0)))
そう、等比数列で扱えるのはピッチ(Pitch)4の添字単位(Index Unit)までで、周回単位(Cycle Unit)内における分布(Distribution)自体は(配置されるそれぞれの点が関数Y=XあるいはY=-Xに従うだけで)全然等比的ではないのです(だから上掲のアニメーションもよく見ると回転がぎこちない)。考え方としては円のN回転を周回単位に設定すると添字単位が「1周,2周,3周…」と自然数や整数の範囲に収まって等比数列(すなわち自然数集合や整数環)で数えられるのと同じです。いわゆる桁上がり(Carry)の概念ですね。
【初心者向け】添字化(Indexing)と単位化(Unitization)
【初心者向け】N進法(N-ary)とp進数(p-adic)

その一方でCos(θ)+abs(Cos(θ))i関数とSin(θ)+abs(Sin(θ))i関数は同一座標軸状に並べてみると実は全くの同型。それを前者はX-Y軸、後者はY-Z軸に配するので90度の位相のズレが発生する訳です。そしてこうして1次関数(Linear Function)的に扱えるという事は(偶関数に見える上掲の関数中においてピッチ2に対する1の補正を与えているところから見ても)、この関数が元来は原点を始点に共役座標を円錐状に展開する奇関数(Odd Function)である事は明らかです。
【初心者向け】線形関数や絶対値関数


ここまで明らかになれば自明の場合として、以下の様な(一次関数の構築する)円錐型座標系(Cone Coordinate System)と(三角関数が構築する)極座標系(Polor Coordinate System)の関係が浮かび上がってくる訳です。イメージ的には「(一対の円錐で構成される)円錐座標系の共役線の1本を直径とする円盤が円錐に直角に取り付けられてる感じ」辺り?

Cos_Waltz01<-function(Radius){
# 格子描画
grx=seq(-3,3,length=4)
gry01=rep(c(-1,1),2)
gry02=rep(c(1,-1),2)
plot(grx,gry01,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="Cosine Waltz",xlab="x=-Cos(θ)→Sin(θ)→Cos(θ)→Sin(θ)→-Cos(θ)",ylab="Cos(θ)",col=rgb(0,0,0))
par(new=T)
plot(grx,gry02,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,0))
# 円描画
c0<-seq(0,pi*2,length=61)
cy<-cos(c0)
cx00<-cos(c0-pi*Radius)
cx01<-cos(c0-pi*Radius)-2
cx02<-cos(pi*Radius-c0)+2
par(new=T)
plot(cx00,cy,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
for(i in 1:61)
{
segments(0,0,cx00[i],cy[i],col=rgb(0,1,0))
}
# 補助線
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
}
# アニメーション
library("animation")
Time_Code=seq(0, 4,length=61)
saveGIF({
for (i in Time_Code[1:60]){
Cos_Waltz01(i)
}
}, interval = 0.1, movie.name = "Cos_Waltz04.gif")
Cos_Waltz01<-function(Radius){
# 格子描画
grx=seq(-3,3,length=4)
gry01=rep(c(-1,1),2)
gry02=rep(c(1,-1),2)
plot(grx,gry01,type="l",xlim=c(-3,3),ylim=c(-1,1),main="Cosine Waltz",xlab="x=-Cos(θ)→Sin(θ)→Cos(θ)→Sin(θ)→-Cos(θ)",ylab="Cos(θ)",col=rgb(0,0,0))
par(new=T)
plot(grx,gry02,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,0))
# 円描画
c0<-seq(0,pi*2,length=61)
cy<-cos(c0)
cx00<-cos(c0-pi*Radius)
cx01<-cos(c0-pi*Radius)-2
cx02<-cos(pi*Radius-c0)+2
par(new=T)
plot(cx00,cy,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)
plot(cx01,cy,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(cx02,cy,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
for(i in 1:61)
{
segments(0,0,cx00[i],cy[i],col=rgb(0,1,0))
}
for(i in 1:61)
{
segments(-2,0,cx01[i],cy[i],col=rgb(1,0,0))
}
for(i in 1:61)
{
segments(2,0,cx02[i],cy[i],col=rgb(0,0,1))
}
# 補助線
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
}
# アニメーション
library("animation")
Time_Code=seq(0, 4,length=61)
saveGIF({
for (i in Time_Code[1:60]){
Cos_Waltz01(i)
}
}, interval = 0.1, movie.name = "Cos_Waltz03.gif")
①相関係数概念(Orrelation Coefficient Concept)においては-1→1の範囲のみを抽出して以下の解釈を適用している。
相関係数 - Wikipedia
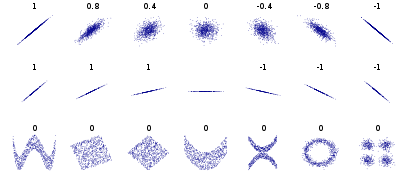
(x, y) の組とそれぞれの相関係数を示している。相関は非線形性および直線関係の向きを反映するが(上段)、その関係の傾きや(中段)、非直線関係の多くの面も反映しない(下段)。中央の図の傾きは0であるが、この場合はYの分散が0であるため相関係数は定義されない。
- -1(cos(θ)-cos(θ)iつまりy=-x)…負の相関の極限
- 0(cos(θ)+Sin(θ)iつまり円)…無相関
- 1(cos(θ)+cos(θ)iつまりy=x)…正の相関の極限
それぞれの極座標系に原点を中心とする正規分布(Normal Distribution)データなどを配して関係を割り出そうとしているイメージ。
【初心者向け】正規分布とは何か?


【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。


【初心者向け】記述統計学と代表値
②オイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)は、現段階では概ね「観測原点のみの0次元段階から出発し、(統計的手法のみが便りの)1次元(1辺形)段階を経て(円弧/球面座標における対蹠/直径を見出して導入可能な数理が急増する)2辺形から6辺形にかけて複雑な平面的/立体的幾何展開があり、以降は原則として半径1の円弧への完全合一を果たすまで単層トーラスの小半径(Minor Radius)の無限小に向けての収束が続くのみ」と見えているが(概ね素数2^n族と素数3^n族の振る舞いに着目した結果素数)、上掲アニメーションを眺める限り、どうやらこのサイクル自体を周期単位(Cycle Unit)とする添字単位(Index Unit)の展開、すなわち桁上がり(Carry)や桁下がり(Borrow)も想定も可能な様である。これからの研究課題。
【Rで球面幾何学】二辺形一辺形?
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…
【初心者向け】添字化と単位化
【初心者向け】N進法(N-ary)とp進数(p-adic)

そんな感じで以下続報…