【数理考古学】群論とシミュレーション原理①これまでの投稿内容のまとめ。
吃驚するほどグチャグチャになってしまったので整理を試みます。
ガウスの巡回群(Gauss Cyclic Group)
「正n角形の作図からコンパスと定規を追放した」と言われる、コンピューターグラフィック史上最も重要な演算結果集合の一つ。群論においては、この演算こそが「半径1の単位円」を観測結果集合とする円周群=リー群$S_0$=1次元トーラスのコンストラクタ(初期化定義)に指定されています。
1の冪根 - Wikipedia
1の冪根は全て、複素数平面における単位円周上にある。また概要で述べたことより、1のn乗根の全体は位数nの巡回群である。これは円周群の正規部分群である。
1のn乗根は、複素数平面では、単位円に内接する正n角形の頂点である
代数学的背景はこんな感じ。
【数理考古学】代数方程式について。
数学において公式(Fomura)とは多くの場合恒等式(Identity)を意味するが、その定義は「どの様な値を代入しても両辺が等しくなる」式である。
これに対し「ある特定の値でなければ統合が成立しない式」を方程式(Equatation)と呼び、その値を根(Root)あるいは解(Solution)と言う。
未知数xを含む方程式(Formula)f(x)=0には様々な形式があり、このうち代数的演算(Algebraic operations、加減算、乗除算、冪根)を有限回用いて表せるものを代数方程式(Algebraic Formula)という。
大数学者ガウス(C.F.Gauss, 1777年〜1855年 )は「n次代数方程式はn個の根を複素数の範囲に持つ」事を証明した。これは代数学の基本定理と呼ばれている(ただし四次以上の方程式の解は代数的には求められない)。
①「ガウスの巡回群」を図示化した正n角形には興味深い特徴がある。これを元gとして逆元$g^{−1}$を求めると次数が2n+1(奇数)の場合重ならず、倍の次数2(2n+1)(偶数)で初めて統合されるのである。
【Python演算処理】単位トーラスを巡る数理②トーラス群の設定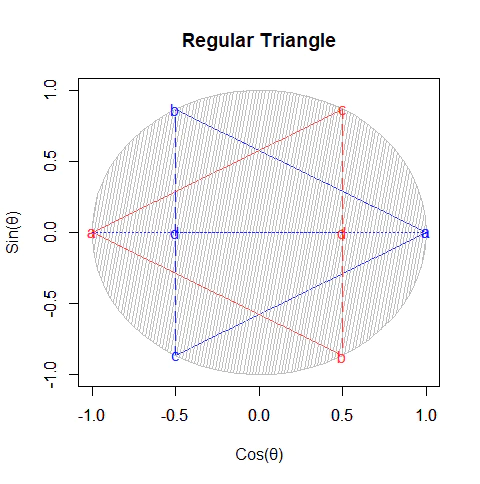
以下の計算結果も、この数理と密接な関係にある。
cos(π)=-1\\cos(\frac{π}{2})=0\\cos(\frac{π}{3})=\frac{1}{2}\\cos(\frac{π}{5})+cos(\frac{3π}{5})=\frac{1}{2}\\cos(\frac{π}{7})+cos(\frac{3π}{7})+cos(\frac{5π}{7})=\frac{1}{2}\\cos(\frac{π}{9})+cos(\frac{3π}{9})+cos(\frac{5π}{9})+cos(\frac{7π}{9})=\frac{1}{2}\\cos(\frac{π}{11})+cos(\frac{3π}{11})+cos(\frac{5π}{11})+cos(\frac{7π}{11})+cos(\frac{9π}{11})=\frac{1}{2}
要するに自然数集合(Natural Set)$\mathbb{N}$に単位元(Identity Element)0と逆元(Inverse Element)$\mathbb{N}^{-1}$を加え整数群(Integer Set)に発展させる時、ガウスの巡回群の元と逆元は半径1の単位円上にかかる一対の奇数図形を描き続けるので、その頂点のコサイン値の総和もそれぞれ$\frac{1}{2}$となり続けるのである。最終的に正n角形のnが∞に到達すると$\frac{∞}{2}=∞$が成立してかかる半減は意識されなくなるが、これこそがまさに共役概念(Conjugated Concept)の出発地点といえよう。
位相が等差数列である三角関数の和の公式
以下の数理もこうした全体像の一部と推察される。
【数理考古学】とある円周率への挑戦?
【数理考古学】解析学史に「虚数概念」をもたらした交代級数
ライプニッツ級数(Leibniz series,1674年,グレゴリー級数がx=1の場合)
\sum_{n}^{\infty}\frac{-1^n}{2n+1}=\frac{π}{4}
グレゴリー級数(Gregory series, 1671年)
\sum_{n}^{\infty}\frac{-1^n}{2n+1}x^{2n+1}=\frac{π}{4}
ちなみに
\sin(π)=0\\
\sin(\frac{π}{2})=1\\
\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}(0.8660254)\\
\sin(\frac{π}{5})+\sin(\frac{3π}{5})=\frac{\sqrt{5+2\sqrt{5}}}{2}(1.538842)
> round(sin(pi),digits=8)
[1] 0
> round(sin(pi/2),digits=8)
[1] 1
> round(sin(pi/3),digits=8)
[1] 0.8660254
> sqrt(3)/2
[1] 0.8660254
> round(sin(pi/5)+sin((3*pi)/5),digits=8)
[1] 1.538842
> sqrt(5+2*sqrt(5))/2
[1] 1.538842
> round(sin(pi/7)+sin((3*pi)/7)+sin((5*pi)/7),digits=8)
[1] 2.190643
# 現時点の私にはこの数値解に該当する式が見つけられない!!
>round(sin(pi/9)+sin((3*pi)/9)+sin((5*pi)/9)+sin((7*pi)/9),digits=8)
[1] 2.835641
# 現時点の私にはこの数値解に該当する式が見つけられない!!
> round(sin(pi/11)+sin((3*pi)/11)+sin((5*pi)/11)+sin((7*pi)/11)+sin((9*pi)/11),digits=8)
[1] 3.477576
# 現時点の私にはこの数値解に該当する式が見つけられない!!
- この計算にどういう意味があるか現時点の私には分からない。
②複素数概念の導入が不可避となるのは三次方程式以上となる。
[【数理考古学】三次方程式から虚数へ。]
(https://qiita.com/ochimusha01/items/f1f6d436f589d6b5b2fd)
幾何学的には三角不等式(Triangle Inequality)$‖x+y‖ \leqq ‖x‖+‖y‖$が成立し面積の概念が生じる「円周上の三点以上の操作」に対応? そして幸いにも四点までの操作なら「ターレスの定理」により直角の概念が使えるのである。
【初心者向け】「三角不等式の体感方法?


この様な数学的背景など知らなくても、(代数学的方法では求められないn次方程式を数値的に導出する)以下の計算方法に馴染みがある人なら少なくないはずです。
- 2πを角数n+1で割った集合θを作る。
- それぞれのCos(θ)を求めX軸に置き、Sin(θ)を求めY軸に置く。
群論上の表現では以下の様になる様です。
群と表現の話
- 無限の場合は$\mathbb{Z}$。
- 有限の場合を加法的に表現すると$\frac{\mathbb{Z}}{n\mathbb{Z}}=(0,1,…,n-1)$
- 乗法的に表現すると$C_n=(e^{\frac{kπi}{n}}|0 \leqq k \leqq n-1)$
そしてこの演算群を導入すると、以下の様な計算も可能となるのです。
【初心者向け】挟み撃ち定理による円周率πの近似
一辺の長さがaの正n角形に外接する円の半径r
- $r=\frac{a}{2\tan(\frac{π}{n})}$
- $a=r(2\tan(\frac{π}{n}))$
一辺の長さがAの正n角形に内接する円の半径R
- $R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
- $A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$
一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係
- $r=Rcos(\frac{π}{n})$
- $R=\frac{r}{cos(\frac{π}{n})}$
外接円を単位円(Unit Circle)としたのが上記アニメーション。
- 外接円の半径Rは単位円の定義に従って1
- これに内接する正多辺形の1辺の長さAは$2\tan(\frac{π}{辺数})\cos(\frac{π}{辺数})$
- 外接円に内接する正多辺形の内接円の半径rは$\cos(\frac{π}{辺数})$
この演算の極限には半径1の単位円の場合における円周長として2πが現れます。半径rの場合に一般化すると算数段階で習う2πrとなりますね。
そんな感じで以下続報…

