Qiitaで投稿を始めた1年前より試み続けてきた「コンピューター・プログラミングへの群論の援用」概念(Concept)の現段階におけるまとめ。全体像を俯瞰すると(関数列のそれを含む)演算結果集合(Operation Result Set)は、それが族(Family)とする観察結果集合(Ovservation Result Set)と「それなりの精度で一致する」限り有効であるとする考え方がますます鍵となってきた様です。それ自体は「様々な自然現象を偏微分方程式の形で表す事が可能だが、ここで重要となるのは式形そのものというより、演算結果がどれだけ現実の観察結果を近似出来ているかである」とするシミュレーション原理(Simulation Principle)の言い換えに過ぎません。
シミュレーション - Wikipedia
ラテン語の 「シミリス(similis=似ている)」「シミュラーレ(simulare=模倣する)」「シミュラット(Simulat=真似た、コピーした)」といった用語から生まれた概念である。対象となるシステムで働いている法則を推定・抽出し、それを真似るようにして組み込んだモデル、模型、コンピュータプログラムなどを用いて行われる。現実のシステムを動かしてその挙動や結果を確かめることが困難、不可能、または危険である場合に用いられる。
例えば、社会現象などにおける問題の解決方法を探る時など、(悪影響があるので実社会ではとりあえず試せないので)実際の社会と似た状況を数式などで作りだし、コンピュータ等を用いて模擬的に動かし、その特性などを把握するのに用いる。例えば風洞実験、水槽実験で働いている法則を数学的なモデルに置き換えて行う。また例えば経営に関する様々な事象を数学的なモデルに置き換えてみて、様々な数値を入力したり変化させることで、結果を推定する。
シミュレーションのための装置やプログラムをシミュレータ(Simulator) と言う。ただし、きわめて単純なシステムを模倣するためのシミュレーション、特に単純化されたモデルを用いる場合などは(とりあえず)紙と鉛筆(やホワイトボードとペン)だけを用いて手作業で行われるものもある。
対象となるシステムにおいて働いている法則をどれほど忠実に模倣するかによって、シミュレーションの精度は異なる。シミュレーションの質は、シミューレーションを設計する者の技量や、どの程度まで法則を見抜き、どこまでそれらの法則を模倣させたか、ということによって異なるのである。現実の法則を十分に模倣していないシミュレーションは、現実とは異なった挙動を示す。またコンピュータを用いて、連続現象を離散化した積算によるシミュレーションは必ず誤差が生じ、その誤差は蓄積する。従ってコンピュータによるシミュレーションによって良好な結果を得る為には、モデル化による誤差見積もりが重要となる。モデル化によるシミュレーションは、現象についてどの程度正確に真似るかによって計算量を調整することが可能であり、現象についての完全な知識は必要とされないなどのメリットがある。
システムのモデル化を行わず、完全な模倣を目的とする場合は、シミュレーションと言わずエミュレーションということもある。エミュレーションは、模倣したいシステムにおいて、予測できる現象より予測できない現象が支配的である場合などに使われる。
【Python演算処理】単位トーラスを巡る数理①平坦トーラスとの往復



【Python演算処理】単位トーラスを巡る数理②トーラス群の設定



こうした投稿で語ってきた内容程度、おそらく以下の様な数学上の抽象表現で既に語り尽くされた範疇に含まれてるのです。しかし難解過ぎて現時点の私のレベルではそれを確かめる事も出来ません。
多元数について8枚のスライドでまとめてみたら
絶対値1の複素数$e^{iθ}$は円周群と呼ばれるリー群(連続群)になる。指数の肩iθをリー代数と呼び、iを生成子と呼ぶ。リー群について考えるよりも、リー群の単位元1における接空間におけるリー代数を考える方が見通しが良い。円周群$f(θ)=r^{iθ}$においては$f'(0)=i$が生成子で、リー代数iθは1から見た接線である。生成子は次元の数だけあり、円周が1次元の線なので、円周群の生成子は1個である。これにもう一つの虚数単位の組j,kを追加したのが四元数となる。
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか?
複素数平面において中心0、半径1の円周は複素数の積に関してリー群である。
0次元球面$S_0$,1次元球面$S_1$および3次元球面$S_3$は、これらをそれぞれ絶対値が 1 の実数全体、複素数全体、四元数全体と同一視することでリー群にすることができる。他の次元の球面ではこのようなことはできないし、リー群にはならない。リー群としての$S_1$はしばしば円周群と呼ばれる。いくつかの円周群同士の直積リー群はトーラス群と呼ばれる。
円周群は角θによる媒介変数表示が可能で、写像$θ→z=e^{iθ}=\cos(θ)+\sin(θ)i$は円周群に対する指数写像となる。
円周群Tの回転群としての解釈は、標準位相に関して円周群が一次元トーラスに位相群として同型であるという事実に発する。より一般に、Tのn重直積群$T_n$は幾何学的にn次元トーラスである(1次元トーラスは円周群と同じ! そんな考え方もあるのか!)。
CV・CG・ロボティクスのためのリー群・リー代数入門: (1) リー群
ざっくりと言うと,回転を考えるというのはある種の「曲がった空間」を考えることであって,理論上も実用上も面倒な点が多い.ところがここで,回転が「群」と呼ばれる数学的構造を持っていることに着目すると,さっきの「曲がった空間」に関する問題を,それに対応する「真っ直ぐな空間」に関する問題に置き換えて考えることができる.ここで言う「曲がった空間」がリー群であり,「真っ直ぐな空間」がリー代数と呼ばれるものであり,それらの間の対応を表すのが指数写像と呼ばれるものである。
リー群のイメージ.青い小さな丸が単位元I
3次元回転は順序を入れ替えると結果が変わる。
リー群の単位元における接空間
なので今はとりあえず自分なりの表現で全体像を把握する努力を続けざるを得ません。まぁ経験的にいってそのうち「ああアレはこの事だったのか!!」と気づいて愕然となる羽目に陥るのはわかり切っている訳ですが…
「観察者の主観」なる曖昧過ぎる基準からの出発とその排除。
この様にリー群や円周群の定義との関わりを明らかに出来ないまま、とりあえず「N次元上において特定の観測原点から全方角に向けて等距離にある観測球面(Observation Sphere)」を元とする観測結果集合(Ovservation Result Set)から出発したいと思います。
- 考え方としては全方角均等に観測が成立しない(データはあっても名義尺度止まりだったり、有意の相関関係が一切見出せなかったりする)場合も含む。
【数理考古学】とある実数列(Real Sequance)の規定例③オイラーの等式(Eulerian identity)e^πi=-1が意味するもの?
空積概念(Empty/Nullary Product Concept=乗法単位元1の起源)
空和概念(Empty/Nullary Sum Concept=加法単位元0の起源) - 実際、二評価軸間の相関係数を示す確率楕円も、両者が完全に無関係な場合には「内積0=直交状態」となり真円を描くのである。出発点はまさにこのイメージだが、ここでは既に二軸で考えている。ならばさらに遡って1軸で考えるとどう見えるだろうか?
【初心者向け】方形描画関数①三角関数との関係。

この考え方を具体的にプログラミング言語で実装してみた結果が以下。
【初心者向け】複素共役のアニメーション表示について。
- 以下のアニメーションは、観察者の主観によって「外向き/内向き」[左向き/右向き]「上向き/下向き」に進行している様に映るが(その向きも、首を振っただけで釣られて変動する)、実はそもそもアニメーションの中割り自体に進行方向を示唆する情報が含まれていないのである。
- 同様の理由で以下のアニメーションも、油断するとすぐ「周回運動」か「正面をこちらに向けたままの往復運動」か分からなくなってしまう。
【Python演算処理】単位球面を巡る数理②そして単位トーラスへ
こちらの画像なら普通の人はまず見間違えない。
だが、以下の画像だけ差し出された場合はどうだろう? プログラムされた運動内容自体は同じだが、実はこのアニメーション自体もまたそもそも両状態を峻別する情報を含んでいないので、観測者側の主観によって観測結果が揺れ動く(実は上掲の「観測楕円」アニメーションもこの類)。
こうした状況はいわゆる複素共役(Complex Conjugate)の概念と密接に結びついている。その一方で、かかる「主観問題」は、しばしば再燃する量子力学的不安定性についての議論において混乱の核となる。
数学者のための量子力学入門 - これと真逆のケースが「誤差関数(ERF=Error Function)」を円尺に射影した場合に観測される。
【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。
上掲の「共役球面」においては観測限界(Ovservation Rimit)を手前の観測原点(Ovservation Limit)の対蹠に置いて「赤道よりこちら側」のみを可視範囲としているが(実際には観察者の視界は水平線/地平線の向こう側までは及ばないから、これもインチキといえばインチキである!!)、この射影においては「球面」の辺縁が観測限界と設定され、すなわち光の進路さえ曲げるブラックホールの重力レンズ効果の様に「球面の裏側まで映り込んでいる」状態。とはいえ観測者側の主観はそんなケースなど想定していないのであっけなく追加情報を切り捨ててしまい、ただの球面と見てしまうのである。
『インターステラー』科学的背景に基づいたブラックホール表現への挑戦
そういえば、そもそも誤差関数(ERF)や相補誤差関数 (ERFC)は、数聖ガウスが中心極限定理(CLT=Central Limit Theorem)に従って、外れ値に弱い最小二乗法からそれを除去する為に考案されたものだった。その意味合いにおいてなら、こうした観測者の態度は十分理にかなっている。ところがその延長線上に現れた正規分布(Normal Distribution)概念は、むしろ逆に帰無仮説における「有意の差が見られない場合の検証」などに用いられる様になっていく。こちらのニュアンスは、上掲の「(有意な観測結果が得られない状態としての)空集合」の定義と重なっていく。
【無限遠点を巡る数理】無限遠点(Infinity)としての正規分布と分散概念の歴史
かかる意味論上の境界線(Semantic Borderline)については、フーリエ級数における「望む波形の生成方法」を学ぶ過程でも痛切に感じたものである。究極的には「浜辺に描かれた砂文字の様に」その波形自体の減衰や(多くの分布がサンプル数増大によって正規分布に回帰していく様に)無意味情報(Noise)の海に改めて併呑されていく儚さ…
【初心者向け】フーリエ解析を可視化する。
ところが実際に「減衰」の概念を導入したフーリエ変換やラプラス変換では、その結果が(絶対値1の円周群のみを対象とする)リー群へと回帰するどころか(公比が-1以上か以下の等差数列、あるいは静止軌道から外れた人工衛星の様に)むしろ究極的にはそれから逸脱していくイメージすら内包しているのである(畳み込み(Convolution)概念の起源。ただしラプラス変換の元=演算結果集合は回路方程式であり、こちらはこちらで独自の定常状態への回帰が主張される)。この辺りの境界線の見極めが難しい。
【Python演算処理】ラプラス変換/ラプラス逆変換を試す。
【数理考古学】とある実数列の規定例④フーリエ族とラプラス族概念の追加?
この様に元こそ何ともあやふやですが、むしろだからこそ、そこから有意味な円形性や球面性を抽出する演算の研究が古くから発達し、多種多様な群=演算結果集合(Operation Ewsult Set)を下属させてきたとも言える訳です。
族(Family)の分類とそれに下属する演算集合の関係の整理
以下にまとめて直してみました。
【数理考古学】群論とシミュレーション原理⑧族の分類とそれに下属する演算集合の関係の整理
①ピタゴラスの定理(Pythagorean Theorem)$半径r^2=x^2+y^2+z^2+…$がなす球状集合は、二次元上でこそリー群に分類される1次元トーラス$S_0$(円周群)と演算結果が重なるが、2次元トーラス$S_1$(複素数全体の集合)や、3次元トーラス$S_3$(四元数全体の集合)と直接呼応する訳ではない。
【数理考古学】群論とシミュレーション原理⑥二次元トーラス概念への発展



②三次元極座標系(3D Polar Coordinate System)(半径r,水平角φ,垂直角θ)は、三次元トーラス多様体$S_3$=四元数(Quaternion)上における「縦回転も横回転も伴わない場合(すなわ大半径Rに直交する交点を中心に±Rの線分伸ばした接線の両端を対蹠に取った場合)」がなす球状集合に該当する。そう、ここから円描画に関係する単振動(Simple Vibration)概念が、偶数系$-1 \rightleftharpoons n \rightleftharpoons +1$と奇数系$0 \rightleftharpoons n \rightleftharpoons 2$の2種類存在する事が俄然意味を持ち始めるのである。
【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ

- ここで引いた「補助線」は、等速円運動(Constant Velocity Circular Motion)やオイラーの公式(Eulerian formula)$e^{θi}=\cos(θ)+\sin(θ)i$が立脚する「1軸で回転する円状/球状集合」の概念に由来する。
【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式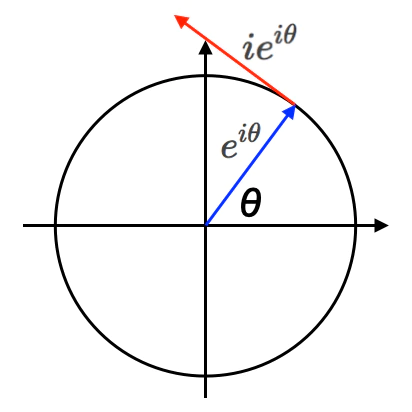
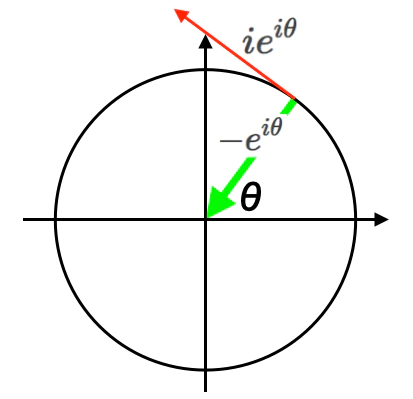
- そしてかかる「1軸で回転する円状/球状集合」に2番目の直行回転軸を与えると、両者の合成結果として3番目の直行回転軸が勝手に追加されるのが三次元トーラス多様体$S_3$=四元数(Quaternion)概念の基本原理となる(リー群$S_1$の次が$S_2$でなく$S_3$なのはこの為)。。
【数理考古学】群論とシミュレーション原理⑦三次元トーラスとしての四元数概念導入
そう、ここで(それ自体は原則として閉じた無限反復運動に過ぎない筈の)複式簿記の記法で対象法人の盛衰を語る管理会計のアプローチ同様、(やはりそれ自体は閉じた無限反復運動の一種に過ぎない筈の)「独楽(こま)の摺漕ぎ運動」を前後左右の水平運動につなげる物理学の記法が「虚無=単調な無限反復運動から脱却する運動」として浮上してくるのです。
フーリエ級数(Fourier Series)
こちらでまとめて解説しています。
【初心者向け】フーリエ解析を可視化する。
テイラー級数(Taylor Series)/マクローリン級数(Maclaurin Series)概念の応用。
【数理考古学】オイラーの公式を導出したマクローリン級数の限界?

オイラーの法則を応用して望む波形を近似する操作自体はピタゴラス族からの逸脱を意味しますが、その操作概念自体は(検算上「貸方]と「借方」の数字が一致する)複式簿記に近く、かつまた上掲の様に究極的には「浜辺に描かれた砂文字の様に」その波形自体の減衰や(多くの分布がサンプル数増大によって正規分布に回帰していく様に)無意味情報(Noise)の海への併呑によってピタゴラス族へと回帰していきます。また、この数理については特別に「(かかる操作の)有意味性(Meaningfulness…観察者の主観から見て特徴ある形を近似してたり、その波形を再生すると特定の音が出たりする事)」が問われる場合もあるのを忘れてはなりません。



フーリエ変換(FT=Fourier Transform)とラプラス変換(FT=Laplace Transform)
こちらでまとめて解説しています。
【数理考古学】とある実数列の規定例④フーリエ族とラプラス族概念の追加?
どちらも「整数倍の無限周期関数しか扱えない」フーリエ級数の弱点を収束因子(Convergent Factor)要素追加によって克服しようというアプローチである点は同じです。逆をいえば、その代償として「ピタゴラス族への回帰」要素をあっけなく捨て去ってしまうのです。
フーリエ変換/逆変換(収束因子e^-iωt)
F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i \omega t}dt\\
f(t)=\frac{1}{2π} \int_{-\infty}^{\infty} F(\omega) e^{-i \omega t}d\omega
- 「時間推移に伴う周波数領域(スペクトル)の変遷」を扱う**離散フーリエ変換(DFT=Discrete Fourier Transform)**同様(光の波長ごとの屈折率の違いを利用してプリズムによって分光する様に)周波数スペクトル解析(Frequency Spectrum Analysis)を遂行し、かつまたそれに加えられた操作を元波形に反映させるイコライザーの動作原理の一部。
【数理考古学】音楽と離散フーリエ変換(DFT)

- 「無限に繰り返されない=一定時間内のみ観測される」波形を捉えられる様になった代償として、無限周期関数そのものは「その波形のスペクトルの振幅が無限大に限りなく近づいていく」デュラックのデルタ関数(Dirac Delta Function)めいた振る舞いを見せる様になる。
【数理考古学】ディラックのデルタ関数とヘヴィサイドのステップ関数
ラプラス変換/逆変換(収束因子e^-st)
F(s)=\int_{0}^{\infty} f(t) e^{-st} dt\\
F(s)=\mathcal{L}[f(t)]\\
f(t)=\mathcal{L}^{-1}[F(s)]
その演算内容こそ既存のフーリエ級数の拡張に過ぎない一方、ラプラス変換の元=観察結果集合/演算結果集合は、ピタゴラス群から回路方程式へと差し替えられています。こちらはこちらで独自の定常状態への回帰を特徴とし、指数冪関数$e^{iθ}$からの援用はあくまで「微分演算がiωに、積分演算が1/iωに変換される事によって計算が楽になる」といったテクニカルな部分に留まるのです。
そして近代数学が始まる?
そういえば19世紀後半~20世紀前半にかけては「極限の証明技法」としてε-δ論法が急激な発展を遂げてきた時代だったのです。
ε-δ論法(イプシロンデルタろんぽう、(ε, δ)-definition of limit)とは、解析学において、(有限な)実数値のみを用いて極限を定義する方法である。
その歴史的背景
ニュートンとライプニッツが創設した微分積分学は、無限小(どんな正の実数よりも小さな正の数)や無限大(どんな実数よりも大きな数)といった実数の範囲では定義できない概念を用いている。このような状況はオイラーによって微分積分学が大幅な発展を遂げる18世紀まで継続された。当時の数学者達は級数の発散や収束に関する定義に無頓着なまま理論を発展させていったため、しばしば誤った結論が導かれてしまうことがあった。
19世紀に入るとコーシーやベルナルト・ボルツァーノらによって、厳密な定義に基づいて微分積分学を再構築しようとする試みがなされるようになる。この時期から収束や連続に関する定義は厳密化されていく。ε-δ論法は1860年代のカール・ワイエルシュトラスの講義によって完成されたもので、これによって無限小や無限大という概念を一切使用せずに収束・連続が定義されるようになった。数学史において、微積分学を完成させたとする評価もあるコーシーは『解析教程(Cours d'analyse de l'Ecole royale polytechnique)』 で、ε-δ論法を用いて関数の連続性の定義を行ったが、この時点でも、連続と一様連続の区別はなかったためにコーシーは自著の中でそのことに起因する誤りをおかしている。
なお、ε-δ論法の登場により一度は数学から追放された無限小や無限大を用いる解析も現代では超実数を用いることで正当化され、超準解析(Non-standard analysis または古典的に無限小解析 Infinitesimal analysis とも呼ばれる)という分野で研究されている。
その数学教育における取り扱い。
微積分学の定理の内、特に関数の極限に関する定理は、この ε-δ論法による定義に基づき証明される。言葉を代えれば、ε-δ論法を用いない微分積分学は厳密な定義に基づかないため、数学界では高校数学の段階で ε-δ論法による定義を教えるべきである、という意見もある。一方で、数学以外の、自然科学・工学・経済学・医学・社会学等においては、ε-δ論法による定義に基づく教育を不要と見なす意見もあり、ε-δ論法による定義を教えることの必要性は、数学教育における古くて新しい論争である。
ε-δ論法というのを感情を込めて説明するとこういうことなのだそうだ。「好きなεを持っていらしてください。どんなに小さくても結構ですよ。持っていらしたεに応じて適当なδを出し、所定の不等式が成り立つようにできるだけの準備がこちらにはございます」。へー。
当時は統計学が急激な発展を開始した時代でもありました。
19世紀初頭の統計学は現在のものとは相当に異なる。そもそも,当時統計学(Statistics)という言葉は「国状学」という別の意味で使用されており,Laplace や Gauss の仕事は誤差論という学問カテゴリーに属していた。ここでの誤差とは,天体観測や測量の測定誤差のことである。LaplaceやGaussは天体力学で大きな業績を残し,正規分布の発見などをしているのを思い出してほしい(椎名, 2013)。その後,Quetelet,Galtonらを通じて約半世紀かけて誤差や平均の解釈の変更が行われた。正規分布を「誤差の法則ではなく,純粋な変異の法則(a law of genuine variation)であるとする解釈変更は,19世紀統計思想の中心的な成果であった」(Porter,1986, p. 91,訳書, p. 109)とされる。この解釈変更はまた「確率革命」(Krüger,Daston, & Heidelberger, 1987;Gigerenzer et al.,1989)と呼ばれるこの時代の発展の一翼を担うのであろう。
それでは両者は現代科学の世界において、一体どういう具合に交わるのでしょうか? そういう話に発展していく事が確認できたので、とりあえずは以下続報…








