【Python演算処理】単位トーラス(Unit Torus)を巡る数理①平坦トーラス(Flat Torus)との往復

以下の投稿では複素平面(Complex Plane)上における円周群の概念と等速円運動(Constant Velocity Circular Motion)に共通する数理について調べました。
等速円運動についての物理学と数学の立場の違い?


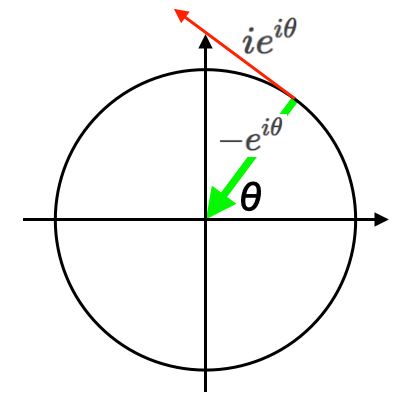
今度は座標系全体に目を向けてみましょう。

#トーラス座標系(Torus coordinate system)なる概念の登場。

この投稿は主に以下を参照しています。
【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！

①まずは両側無限実数列(Both-sides Real Sequence)$Z_n$とその指数写像(Exponential Map)たる片側無限実数列(One-side Real Sequence)$e^n$の関係から出発する。自明の場合として$Z_n$は$e^n$の対数写像(Logarithm Map)となる。
リー環の指数写像 - Wikipedia

解析学の通常の指数関数はリー群Gが正の実数の乗法群（そのリー環は実数全体のなす加法群）のときの指数写像という特別な場合である。リー群の指数写像は通常の指数関数の性質と類似の多くの性質を満たすが、しかしながら、多くの重要な面において異なりもする。

行列指数関数(Matrix Exponential=行列乗) - Wikipedia
行列の対数(Logarithm of a Matrix) - Wikipedia

対数を持つ正方行列(Square Matrix,行要素数と列要素数が一致する正方行列)はいずれかのリー群に属し、かつ、その対数はそのリー群に付随するリー代数の元に対応するため、行列の対数函数の研究はリー理論につながる。指数写像は行列の指数関数で与えられるが、その逆写像は一般に多価となる。対数写像はリー群Gを付随するリー代数gへ写す。

【数理考古学】常用対数表(Table of Common Logarithms)を使った計算

実軸(Real Axis)における乗除算はその対数写像において加減算に置き換えられる。

それぞれの関数の定義域(関数y=f(x)における独立変数xの値)と値域(関数y=f(x)における従属変数yの値)の関係は以下。

Z_n(n=-\infty→-1→0→1→+\infty)=(-\infty,…,-1,…,0,…,1,…,+\infty)\\
e^n(n=-\infty→-1→0→1→+\infty)=(0,…,e^{-1},…,1,…,e^1,…,\infty)

【数理考古学】とある実数列(Real Sequance)の規定例②等比数列から乗法群へ

-\infty→0\\
-1→e^{-1}(0.3678794)\\
0→1\\
1→e^1(2.718282)\\
+\infty→\infty

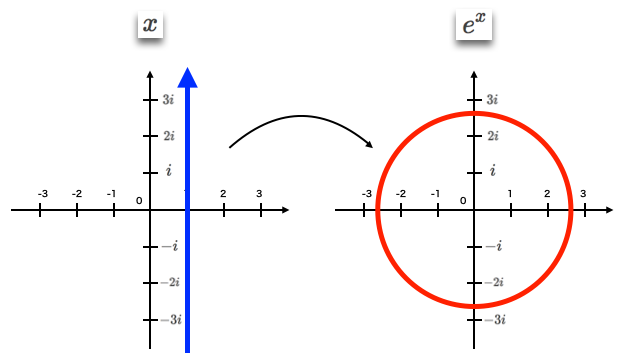
これを「正の実軸上の半直線上に写る元の定義域」は実数直線の任意の点αと考える。

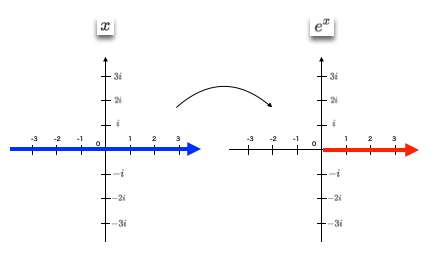
②すると「負の実軸上の半直線上に写る元の定義域」は$α+iπ$とイメージされる。オイラーの等式(Eulerian Identity)$e^{πi}=-1$の世界。

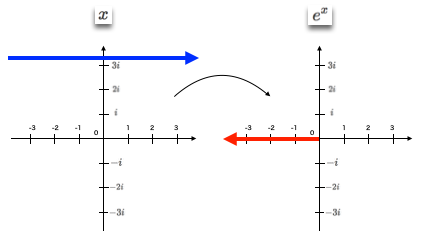
③「正の虚軸上の半直線上に写る元の定義域」は$α+i\frac{π}{2}$ないしは$α-3i\frac{π}{2}$とイメージされる。分枝点切断を行わない座標系では両者が同値となる。

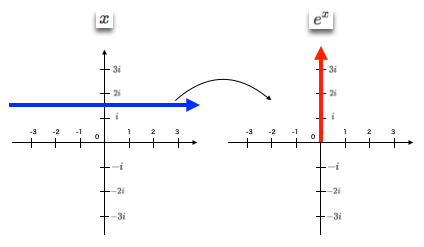
④「正の虚軸上の半直線上に写る元の定義域」は$α+3i\frac{π}{2}$ないしは$α-i\frac{π}{2}$とイメージされる。分枝点切断を行わない座標系では両者が同値となる。

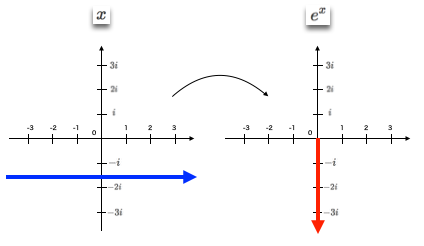
これはまさに複素平面をトーラス座標系として捉える発想に他なりません。
【Python演算処理】単位トーラス(Unit Torus)を巡る数理②トーラス群の設定

確かにトーラス構造を平たく伸ばして「(上下左右の端同士がつながってるコンピューターRPGのワールドマップの様な)平面トーラス」に変換するとこうした座標演算が可能となるのです。こうして展開された平面トーラスは、大半径/小半径それぞれを単位1と置いた場合、それぞれ2π倍の広がりを持つ方形となります。
【ドラクエ1】ワールドマップ（世界地図）とマップ一覧

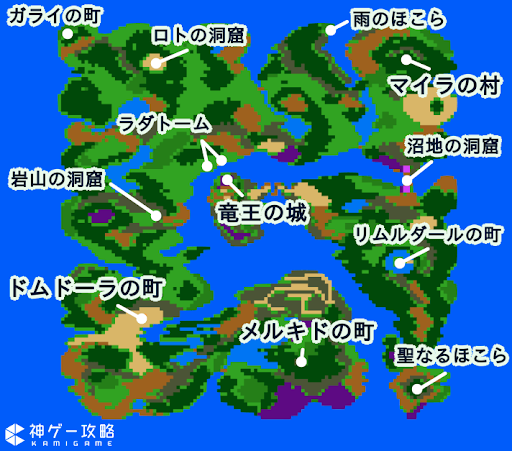
この座標系における垂直移動は、外側から見るとこう見えます。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#描画関数定義
def unit_cylinder(n):
    plt.cla()
    #断面計算
    MiAvD0=[]
    for nm in range(len(MiAvC)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0) 
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)
    #軌跡計算
    Orb_r=abs(MiAvD[n])
    Orb0=[]
    for nm in range(len(MiCvD)):
        Orb0.append(c.rect(Orb_r,Tcode[nm]))
    Orbv=num.array(Orb0)
    Orbh=num.repeat(MiAh[n],61)
    #断面1計算
    MiAvD10=[]
    for nm in range(len(MiAvC)):
        MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
    MiAvD1=num.array(MiAvD10) 
    MiBvD10=[]
    for nm in range(len(MiBx)):
        MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
    MiBvD1=num.array(MiBvD10)
    MiCvD10=[]
    for nm in range(len(MiHz)):
        MiCvD10.append(c.rect(2,Tcode[0]))
    MiCvD1=num.array(MiCvD10)  
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    #中心線描画
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #分割原点
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
    ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)    
    ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
    #アニメーション描画
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="red",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #軌跡描画
    ax.plot(Orbv.real,Orbv.imag,Orbh,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output620.gif", writer="pillow")

この軌道をアイロンでも掛けたかの様に真っ直ぐ伸ばすと円筒座標系(Cylindrical Coordinate System)における以下の動きに対応する訳ですね。
【Python演算処理】単位円筒を巡る数理


この辺りの詳細については、以下で詳しく解説されています。
四元数を用いた三次元回転計算の幾何学的意味

#一般の円座標系との共通点。
この投稿も主に以下を参照しています。
【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！

トーラス座標系も円座標同様に写像元に加えられるスカラー加減算の影響を受ける訳ですが、こちらはむしろ頭を切り替えて円座標が極座標系(Polar Coordinates System)では半径(Radius)rθ(2次元)、rφθ(3次元)と表される数理に拠って考える方がイメージしやすいかもしれません。

①元写像が実数軸の原点で交わる場合、単位スケールそのまま。

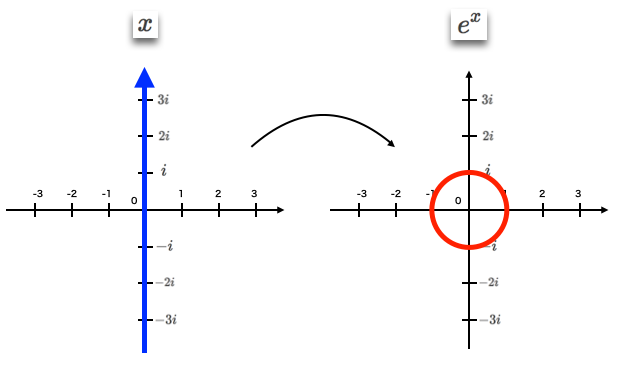
②元写像が実数軸の原点より左(すなわちマイナス方向の位置)で交わる場合、縮小。

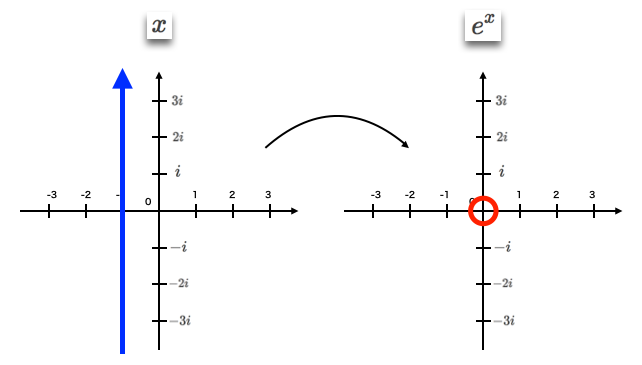
③元写像が実数軸の原点より右(すなわち＋方向の位置)で交わる場合、拡大。

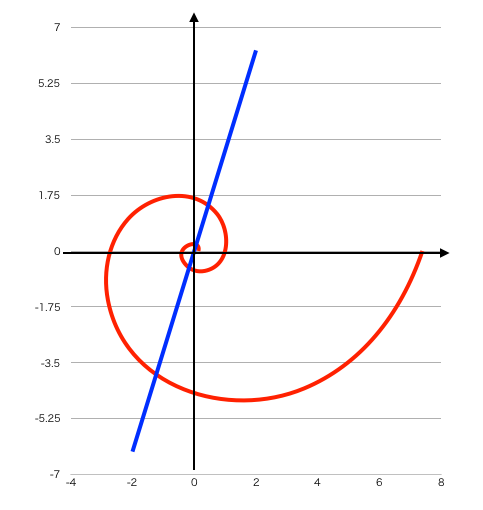
さらに与えられる演算が傾き(Slope)の要素を含む場合、円ではなく螺旋を描きます。これについては円描画関数$-1^n=±i^{2x}$を中心と考える方式に頭を切り替えた方が遥かにイメージしやすいでしょう。

【数理考古学】とある実数列(Real Sequance)の規定例②等比数列から乗法群へ
0>公比>-1の等比数列の場合…どんどん振幅の幅が狭まっていく。

公比<-1の等比数列の場合…どんどん振幅の幅が広がっていく。

どうやらこの辺りの数理はトーラス座標系の拡張形たる円筒座標系(Cylindrical coordinate system)をさらに円錐座標系(Conical Coordinate System)に発展させる際に鍵となってきそうです。

そんな感じで以下続報…