四元数を用いた三次元回転計算の幾何学的意味

任意方向の軸を中心にした三次元回転を計算する際、四元数（クォータニオン、quaternion）を用いる方法がよく使われる。

p' = q p \bar{q}
\\
\left(
q = \cos \frac{\theta}{2} + I \sin \frac{\theta}{2} = e^{I\theta / 2},
\quad I = n_x i + n_y j + n_z k,
\quad |I| = 1
\right)

この方法はオイラー角や回転行列を使う方法よりすっきりしていて、回転を表す $q$ の構築・解読も簡単に行える。一方で、この計算が成り立つことを示す説明は色々あっても、式の直接的な意味を説明していることは少ないように思う。私は以下の疑問を持っていた。

• なぜ左右両方から掛けるのか？
• なぜ半分の角度を用いるのか？
• なぜ共役四元数を用いるのか？
• 四元数を片方だけ掛けた状態は何を表すのか？

掛け算ひとつひとつにまで理屈を求めるのは行き過ぎかもしれないが、もし意味をつけられるならより深い理解に役立つと思う。

ある時Wikipediaの"Rotations in 4-dimensional Euclidean space"を読んでいたら大きなヒントを得たので、その内容を基に自分なりに納得できる解釈をまとめた。（日本語版が無かったため、いくつかの用語は英語のまま抜き出している）

結論

四元数の式は、四次元空間¹での回転操作をそのまま式で表したものと解釈できる。

単位四元数を掛ける

"isoclinic rotation"と呼ばれる種類の四次元回転を計算できる（二次元回転を複素数の積で計算できるようなもの）。この回転は「左右」の区別があり、四元数では掛ける方向によって区別される。

左右両方から掛ける

任意の四次元回転はleft-/right-isoclinic rotationsの組に分解できる。そのため左右から（共役とは限らない）単位四元数を掛けるとあらゆる四次元回転を計算できることになる。

半分の角度を用いる

四次元回転のうちsimple rotationを分解する場合の特徴。目的の回転は $\theta/2 + \theta/2 = \theta$ としつつ、余計な回転は $\theta/2 - \theta/2 = 0$ とキャンセルさせる。

共役四元数を用いる

simple rotationのうち、四元数の実部が表す方向が固定される場合。ふつうは虚部を三次元空間の座標に対応させるので、これは四次元目（実部）の方向が変化しない、つまり三次元回転を表している。

この図は四次元空間上の回転の様子を数学的な手続きに従って三次元に描いたもので、単位四元数の積が表す赤い回転を合成すれば三次元回転と見なせる青い回転が得られることを示している。（詳しい見方は終盤で説明する）

とはいえ「四次元空間での回転」がどういうものなのか分からなければ意味不明な話なので、それについて以降でまとめる。幾何が中心であり四元数の話は軽め。

四次元の回転

そもそも四次元空間を想像することが困難であり、回転の様子を簡単に分かりやすく描くことはできない。しかし数式（回転行列）で表せば、行列が少し大きくなるだけで三次元の場合と見た目は大差ない。そこで、まずは数式の雰囲気から四次元回転の特徴を見ていく。

\left(
\begin{matrix}
x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
R_{11} & R_{12} & R_{13} \\
R_{21} & R_{22} & R_{23} \\
R_{31} & R_{32} & R_{33}
\end{matrix}
\right)
\left(
\begin{matrix}
x \\ y \\ z
\end{matrix}
\right)
\\
\downarrow
\\
\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
R_{00} & R_{01} & R_{02} & R_{03} \\
R_{10} & R_{11} & R_{12} & R_{13} \\
R_{20} & R_{21} & R_{22} & R_{23} \\
R_{30} & R_{31} & R_{32} & R_{33}
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)

4つの軸と2つの平面

本題の前に、四次元の回転を考える際に重要かつ便利な話。

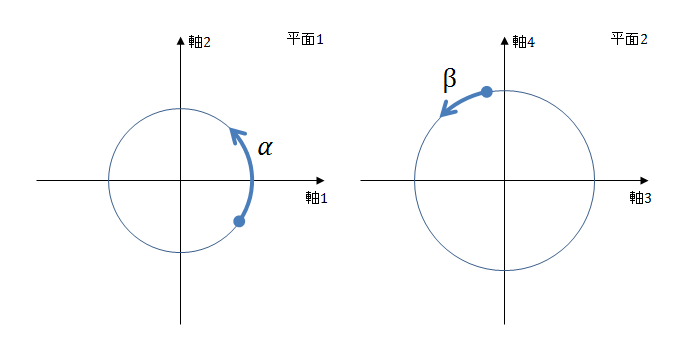
四次元空間では互いに直交する4本の軸を置くことができる。その軸を2本まとめると平面を作れるので、四次元空間では「完全に直交する²2つの平面」を置くこともできる。これを利用すると、四次元空間上の点は4つの一次元的な位置に分解して表せるし、2つの二次元的な位置に分解しても表せる。

互いに直交する4本の軸として座標軸を例にとれば、四次元空間上のある点は、 $w=1$, $x=2$, $y=3$, $z=4$ のように軸ごとに分けた位置で指定してもいいし、 $\left( w, x \right) = \left( 1, 2 \right)$, $\left( y, z \right) = \left( 3, 4 \right)$ のように平面ごとに分けた位置で指定してもいいということ。そして点の動きを考えるときは、 $wx$ 方向と $yz$ 方向に分けるとそれぞれ二次元的な動きとして計算できる。

double rotation

四次元における一般的な回転。三次元には対応するものが無いため想像しにくいが、回転行列で簡単な例³を作ると性質が分かりやすい。

\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
\cos\alpha & -\sin\alpha & 0 & 0 \\
\sin\alpha &  \cos\alpha & 0 & 0 \\
0 & 0 & \cos\beta & -\sin\beta \\
0 & 0 & \sin\beta &  \cos\beta
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)

この例では、 $w$ 軸と $x$ 軸が作る基準面⁴上の点 $\left( w,x,0,0 \right)$ は角度 $\alpha$ だけ面上を二次元回転し、 $y$ 軸と $z$ 軸が作るもうひとつの基準面上の点 $\left( 0,0,y,z \right)$ は $\beta$ だけ面上を二次元回転する。2つの面は完全に直交しているので、このように独立に回転させることができる。そして四次元空間上の各点は、この独立な2つの回転の合成として移動する。

simple rotation

$\beta=0$ （または $\alpha=0$ ）の場合の回転、つまり基準面の片方が固定された状態。1つの面は2本の軸から作れるので、2方向が固定された状態と考えてもいい。

\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
\cos\alpha & -\sin\alpha & 0 & 0 \\
\sin\alpha &  \cos\alpha & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)

二次元回転は固定点を中心とした回転、三次元回転は固定軸を中心とした回転だった。そこから類推すると四次元回転は固定面を中心とする回転⁵だと予想できるが、それはこのsimple rotationに当てはまる。（※この類推はdouble rotationを見逃してしまう）

三次元回転はsimple rotationの特殊例で、軸 $\left( 1,0,0,0 \right)$ と $\left( 0,n_x,n_y,n_z \right)$ が作る面が固定されると解釈できる。言い換えると、三次元回転によって $w$ の値は変わらないし、回転軸 $\vec{n}$ 方向に点が移動することもない。回転行列で表すと、三次元の形に干渉しないようにもう一次元が追加されている。

\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & R_{11} & R_{12} & R_{13} \\
0 & R_{21} & R_{22} & R_{23} \\
0 & R_{31} & R_{32} & R_{33}
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)

isoclinic rotation

$\beta=\pm\alpha$ とした場合の回転。面白い性質をたくさん持つ⁶のだが、これも三次元に無いので意味をつかみづらい。

• （中心以外の）全ての点が角度 $|\alpha|$ だけ移動
• 回転基準面のとりかたが無数に存在
• 回転方向の組み合わせがプラスマイナスの2通り（区別するときはleft-/right-isoclinic rotationと呼称）
• 任意の四次元回転は、left-/right-isoclinicの組で表現可能（後述のisoclinic decomposition）
• 単位四元数を掛けることで計算可能

一般に回転行列は全ての成分がバラバラの数になりがちだが、isoclinic rotationの場合は4つの数（と符号）しか現れない。符号の位置によってleft-isoclinicかright-isoclinicか変わる。

\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
 a & -b & -c & -d \\
 b &  a & -d &  c \\
 c &  d &  a & -b \\
 d & -c &  b &  a \\
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)
\quad または \quad
\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
=
\left(
\begin{matrix}
 p & -q & -r & -s \\
 q &  p &  s & -r \\
 r & -s &  p &  q \\
 s &  r & -q &  p \\
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)

そして、これと同じ計算が四元数でも可能。左右どちらから掛けているかに注意。

\left( w' + x'i + y'j + z'k \right) =
\left\{
\begin{array}{l}
\left( a + bi + cj + dk \right) \left( w + xi + yj + zk \right) \\
\left( w + xi + yj + zk \right) \left( p + qi + rj + sk \right)
\end{array}
\right.

二次元でも同じような話があった。二次元回転は回転行列でも複素数の積でも計算できる。ただし二次元回転は1パターンしか無く、複素数を掛ける順序も関係ない。

\begin{align}
\left(
\begin{matrix}
x' \\ y'
\end{matrix}
\right)
&=
\left(
\begin{matrix}
 a & -b \\
 b &  a \\
\end{matrix}
\right)
\left(
\begin{matrix}
x \\ y
\end{matrix}
\right) \\

\left( x' + y'i \right)
&= \left( a + bi \right) \left( x + yi \right) \\
&= \left( x + yi \right) \left( a + bi \right)
\end{align}

isoclinic decomposition

任意の四次元回転はleft-/right-isoclinic rotationsの組で表せる（＝分解できる）。具体的には、ある回転基準面の組に対して角度 $\left( \alpha, \beta \right)$ というdouble rotationをしたければ、 $\left( \frac{\alpha + \beta}{2}, \frac{\alpha + \beta}{2} \right)$ というleft-isoclinic rotationと $\left( \frac{\alpha - \beta}{2}, -\frac{\alpha - \beta}{2} \right)$ というright-isoclinic rotationをすればいい。同じ基準面に対して続けて回転させるので、leftとrightのどちらを先に行っても結果は同じ。

行列の式で表せば、左右に分解した回転をそれぞれ4x4の行列 $Q_L$, $Q_R$ とすると以下の形になる。具体的に計算しないとピンとこないが、どちらの回転を先に行っても結果が同じということは、2つの回転行列は可換ということになる。

\boldsymbol{p}' = Q_{L} Q_{R} \boldsymbol{p} = Q_{R} Q_{L} \boldsymbol{p}

四元数の式で表せば、左右に分解した回転をそれぞれ単位四元数 $q_{L}$, $q_{R}$ とすると以下の形になる。四元数の積は結合法則を満たすので、どちらの掛け算を先に計算しても結果は同じ。

p' = q_{L} p q_{R}

さらに、 $q_{L}$, $q_{R}$ が共役なら、結果として $p$ の実部（ $w$ ）と虚部（ $x$, $y$, $z$ ）は互いに影響せず、三次元回転となる。これは回転行列に戻して考えると分かりやすい。

\begin{align}
\left( w' + x'i + y'j + z'k \right) &=
\left( a + bi + cj + dk \right)
\left( w + xi + yj + zk \right)
\left( a - bi - cj - dk \right)
\\
\left(
\begin{matrix}
w' \\ x' \\ y' \\ z'
\end{matrix}
\right)
&=
\left(
\begin{matrix}
 a &  b &  c &  d \\
-b &  a & -d &  c \\
-c &  d &  a & -b \\
-d & -c &  b &  a \\
\end{matrix}
\right)
\left(
\begin{matrix}
 a & -b & -c & -d \\
 b &  a & -d &  c \\
 c &  d &  a & -b \\
 d & -c &  b &  a \\
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)
\\
&=
\left(
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & R_{11} & R_{12} & R_{13} \\
0 & R_{21} & R_{22} & R_{23} \\
0 & R_{31} & R_{32} & R_{33}
\end{matrix}
\right)
\left(
\begin{matrix}
w \\ x \\ y \\ z
\end{matrix}
\right)
\qquad \left( \because a^2 + b^2 + c^2 + d^2 = 1 \right)
\end{align}

（追記）コメント欄にて、ここから冒頭の $q = \cos \frac{\theta}{2} + \left( n_x i + n_y j + n_z k \right) \sin \frac{\theta}{2}$ が導かれる理由について質問をいただいた。言葉で説明するとかなり長いため、回答コメントをご覧いただきたい。また、人によっては次節の図示が参考になるかもしれない。

---

なお、分解のしかたは必ず2通りある。 $(q_{L}, q_{R})$ に分解できるなら $(-q_{L}, -q_{R})$ も考えられ、符号反転した四元数単体は角度が 180° 異なるisoclinic rotationを表す。回転を合成すると 180° ± 180° = 360°, 0° となるので区別がつかなくなる。

回転の図示

※この節は混乱しそうなら飛ばしてほしい。四次元の見方は『Dimensions』という動画コンテンツが参考になる。

低次元で図示する方法

例えば三次元の物体を二次元の紙に描こうとすれば、何かの自由度を落とすことで実現できる。写真であれば奥行きを潰し、CTスキャンであればある断面だけを見て、世界地図であれば地球の表面だけを見ている。同じように四次元のものは自由度を落とせば三次元の模型として「描く」ことができるし、その模型をさらに二次元の紙に描くこともできる。自由度を2つ落としていきなり紙に描いてもいい。

図示する段階で座標を変えることもできる。世界地図が分かりやすいが、球面を平面に描く際はどうしても多少の変形を伴う。用途に合わせて便利な投影法がたくさん発明されていて、同じものを図示しても異なる形に見える。

高次元より低次元のほうが扱いやすい一方で、このように情報を落としたり歪めたりしているため、本来あった性質が図では見えなくなったり、逆にウソの性質が見えてしまったりする不都合がある。本記事ではあまり触れないが、できれば図示の影響を理解して何を見ていいのか把握しておく方がいい。

平坦トーラスの展開

double rotationの説明にあったように、四次元空間での回転は独立な2つの二次元回転となっている。つまりある点がどんな角度で回転移動しても、二次元回転の半径にあたる2つの距離が変わらないことになる。さらに言えば、自由度が 4-2=2 でありその点は二次元な面上に居続ける。この面は「平坦トーラス」と呼ばれ伸縮無しで長方形に展開できる性質があるので、上下/左右がつながった二次元の地図として紙に描いて、点が回転移動する様子を見てみる。

地図の緯度方向・経度方向は、2つの基準面それぞれでの円周上の位置を表す。長方形なのは、各基準面上の回転の半径が異なることを反映している。

• double rotation（緑）はトーラス面を斜めに進む。角度が $\left( \alpha, \beta \right)$ であれば、緯度方向に $\alpha$ だけ進む間に経度方向に $\beta$ だけ進む。角度の比が無理数だと何周してもスタート地点には戻らない。
• simple rotation（青）は片方の角度がゼロなので、緯度方向または経度方向のみに移動する。1周で元の位置に戻る。
• isoclinic rotation（赤）は斜めに進むが、緯度経度が同じ大きさで変化するので1周で元の位置に戻る。

double rotationは角度次第でトーラス面上のどこにでも移動できるのに対し、isoclinic rotationでは同じところを回ることしかできない。しかし、実線方向と破線方向の2回に分ければ同様にどこにでも移動できる。分解したときの角度は前節で示した通りだが、角度 $\theta$ のsimple rotation（三次元回転を含む）に対しては2回の角度の大きさを共に $\theta / 2$ とすればいいことも地図からすぐに分かる。

ただ、「共役四元数を用いると三次元回転になる」ということをこれで簡単に図示する方法は思いついていない。回転の向き $\vec{n}$ を図に反映させるために、次は別の方法を使ってみる。

三次元球面のステレオ投影

回転というのは中心からの距離が変わらない移動なので、中心からの距離が等しい「三次元球面」と呼ばれる表面だけを考えれば済む。この面を三次元空間に描くよくある方法が「ステレオ投影」。ちなみに、ステレオ投影で地球表面（二次元球面）を紙（二次元平面）に描く図法は、北極・南極を中心とした地図によく用いられる。

簡単のため、中心が原点で半径1の三次元球面について話していく。北極 $(1,0,0,0)$ が図の中心 $(0,0,0)$ になるようにすれば、投影によって座標は以下の表のように対応する。図における中心からの距離が北極からの離れ具合に対応し、南極は図の無限遠点という扱いになる。三次元回転であれば $w$ が変化しないはずなので、図では中心からの距離が変化しないことになる。

四次元空間上の座標	三次元空間へ投影した座標
$(1,0,0,0)$	$(0,0,0)$
$(w,x,y,z)$	$(x,y,z)/(1+w)$
$(\cos{\theta}, \vec{n} \sin{\theta})$	$\vec{n} \tan{(\theta/2)}$
$(-1,0,0,0)$	無限遠点

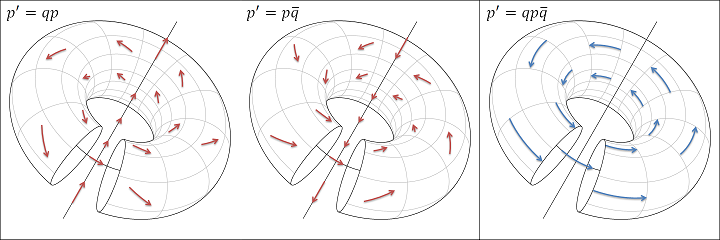
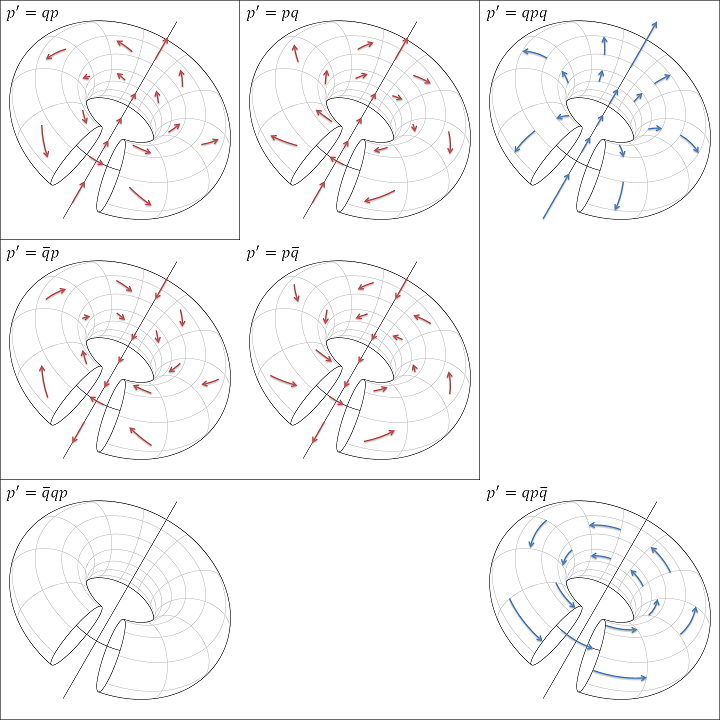
この投影法では前節のトーラス面を一度にたくさん表示でき、下図のようにドーナツを重ねた状態になる⁷（内側を見せるために切断している）。赤い線は各点のisoclinic rotationの軌跡で、実際にはこれが三次元空間を埋め尽くしている。特にドーナツの中心軸となっている直線は、回転を表す単位四元数 $q = \exp{(\vec{n} \theta)}$ の $\vec{n}$ に一致する。

ここで4つのisoclinic rotation $p' = qp, \bar{q}p, pq, p\bar{q}$ を図示してみる。元の四元数の共役を同じ方向から掛けると純粋な逆回転になり、元の四元数を逆方向から掛けると軸は同じで鏡写しのような回転になる。これを組み合わせれば、元の四元数の共役を逆方向から掛けると四次元方向（図では中心からの距離）を元通りにできるため、$p' = q p \bar{q}$ は三次元回転ということになる。

四次元空間で考える利点

三次元の話にわざわざ四次元を持ち出すと何が嬉しいのか。冒頭の結論では数式の疑問を解決する要点のみ書いたので、そこに書きにくかったものを中心にまとめる。

• 「複素数と二次元平面の関係性」と対応をとりやすい
  • 二次元平面を複素数で表すときは実部と虚部の両方を使っていたのに、三次元空間を四元数で表すときは虚部しか使わず実部が謎の存在になっていた。四次元空間で考えれば実部もある意味で対等な扱いになる。
  • 単位複素数の積が二次元回転になっているのと同様に、単位四元数の積は四次元回転（のうちのisoclinic rotation）になっている。どちらも空間上の全ての点を原点中心に同じ角度だけ回転させる。
• 元の数式から発展できる
  • 左右から掛ける単位四元数を共役でなくすれば、任意の四次元回転を計算できる。
  • 三次元空間上の点を四元数で表すときに、実部の値はゼロでなくても（数学的には）構わない。三次元回転ならその値は元に戻るし、他の成分に影響を残すことも無い。
  • あるいは、三次元空間の座標を四元数の実部1つと虚部2つに割り当てることもできる。左右から掛ける単位四元数を適切に構築すれば、余った虚部が影響しない三次元回転を計算できる。

プログラミング向けのメモ

内容は前節と重なってしまっているが、プログラミングに役立ちそうなことを補足しておく。

• 回転させる三次元空間上の点を四元数で表す際、実部を0とすることが多いが、実際は何でも構わない。
  • ただし計算誤差が増える危険がある。
  • それ以前に、式通りに四元数の積を2回計算するのは無駄がある。共役であることや実部が最終的に変わらないことを利用した、計算コスト（掛け算と足し算の回数）がより少ない方法が存在する。
    • 1点だけ回転させるなら、$q = \left( q_s, \vec{q}_v \right)$ などとして $\vec{p}'_v = \vec{p}_v + 2\vec{q}_v \times \left( \vec{q}_v \times \vec{p}_v + q_s \vec{p}_v \right)$
    • 何点も回転させるなら、事前に3×3の回転行列に変換
• 四元数の積を計算できる環境なら、三次元だけでなく任意の四次元回転を計算することにそのまま使える。
  • 左から掛ける四元数と右から掛ける四元数が共役でなくなるので、別々に管理すればいい。
  • 回転の合成をする際は、左用と右用で掛ける向きが異なることに注意。$p' = (q_{L_N} \cdots q_{L_1}) p (q_{R_1} \cdots q_{R_N})$

参考ページ

• Wikipedia
  • Rotations in 4-dimensional Euclidean space
  • Plane of rotation
  • Quaternions and spatial rotation
    • Euler–Rodrigues formula
  • 3-sphere
  • Torus, トーラス
  • ステレオ投影
• DIMENSIONS 日本語版

1. 物理学で出てくる「四次元時空」等ではなく、4番目も対等な長さの次元であるユークリッド空間を考えている。 ↩

2. それぞれの平面上に1本ずつ直線を引くと、その2本の直線は必ず垂直になる。参考ページでは"completely orthogonal"。 ↩

3. 実際のところ、回転に合わせて座標を設定し直すことで全てこの例と同じ形になる。 ↩

4. 参考ページの"invariant plane"や"plane of rotation"（回転不変面）とほぼ同じ。用法を守ると後が説明しづらかったので、本記事ではその用語を用いていない。 ↩

5. より詳細に言うと、固定面上の各点を中心とした、その点を通り固定面と完全に直交する平面上を動く回転。 ↩

6. isoclinic rotationは偶数次元空間に共通して存在するらしいが、本記事では四次元に限った説明をしている。 ↩

7. 太さ一定である必要は無く、一般にはDupin cyclideとして描ける。三次元回転の説明には不要なので詳細は省略する。 ↩