【Python演算処理】単位トーラス(Unit Torus)を巡る数理②トーラス群(Torus Group)の設定

これまでの投稿において、円柱座標系(Cylindrical Coordinate System)で発生する以下の問題の発生に手を焼いてきました。
【Python演算処理】単位円筒を巡る数理

• 周期1で考えるとΓ関数導入が不可避となる。
  
  
• 周期$\frac{1}{2}$で考えると偶奇性(Parity)の概念の導入が不可避となる。
  
  

大半径の周期=小半径の周期の単位トーラス(分岐点1)に分岐点を1つ追加して2分割で場合で考えると前者が「全体の周期も2に引き揚げて各葉ごとの周期1を保つ」場合、後者は「全体の周期を1に据え置いて各葉ごとの周期1が$\frac{1}{2}$になるのを甘受する」場合に相当するのは明らかで、この考え方をさらに3倍($\frac{1}{3}$)4倍($\frac{1}{4}$)と続けていけば群論における元と逆元の関係を構築する事になります。

G_n(n=-\infty→-3→-2→-1→0→1→2→3→+\infty)\\
=(\infty,…,4,…,3,…,2,…,1,…,\frac{1}{2},…,\frac{1}{3},…,\frac{1}{4},…,0)

ところでトーラス座標系は、その全体像を俯瞰すると以下の様な構造になっているのです。
【Python演算処理】単位球面を巡る数理②そして単位トーラスへ

①大半径R=0,小半径r=1の時、単位球面(Unit Sphere)を二重に描く。
②逆に大半径R=1,小半径r=0の時、Z=0となってただの単位円(Unit Circle)となる。

両者の関係は以下となっています。

• トーラスのピッチが$\infty$に限りなく近づく時、大半径Rと小半径rの比は$\frac{\infty}{0}=\infty$に限りなく近づき「二重球面状態」に向かう。
• トーラスのピッチが0に限りなく近づく時、大半径Rと小半径rの比は$\frac{1}{\infty=0}$に限りなく近づき「単円弧状態」に向かう。
• ただしこの考え方では「二重球面状態」や「単円弧状態」自体には到達不可能となるので、その結果得られる観測結果集合(Ovservation Result Set)や演算結果集合(Operation Result Set)はそれらを含まない開集合となる(これにより「二重球面状態」や「単円弧状態」自体は特異点化してしまう？)。

何だか「イプシロン-デルタ論法」めいた定義ですが、そちらの方は難しくて良く分かりません。「一様連続ではない」とは、演算結果が元からはみ出してしまう事？
イプシロン-デルタ論法 - Wikipedia

• ここでは極限を求める演算として「辺長無限小」を求める場合と「頂点数無限大」を求める場合が出てくるが、円の定義は「辺長無限小、頂点数無限大」なので、どちらのアプローチを選んでも同じ最終状態に辿り着く。数学的表現を用いるなら「剰余類として究極的には同値」といった感じ?

• そう、ここで扱う座標系はN次球のそれであり、並大抵の人間には直接それ自体を観想したり操作したりするのが不可能なので1次元ずつ取り出して(誰でも扱える)二次元や三次元空間上のイメージ操作に置き換えてる感じ。それが極限状態に到達するという事はすなわち、次元数の「桁上がり」ないしは「繰り下がり」を意味する様にも思えるが、この辺り並大抵の人間にイメージ可能な内容ではない…

その一方で上掲の添字の振り方なら、分岐点追加によって大半径上に描かれる正n+1角形(ただしNは正の整数)の形も正方向と負方向で一致します。またかかる演算には小半径上の見え方も連動します。
【初心者向け】挟み撃ち定理による円周率πの近似

#一分割(追加分岐点0)ないしは二分割(追加分枝点1)
単位トーラスは一分割(追加分岐点0)の場合も二分割(追加分枝点1)の場合も「内接円と外接円の差」が生じないので大半径には「対蹠間を結ぶ直線(直径)」のみが現れる。
###一分割の場合

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#描画関数定義
def unit_cylinder(n):
    plt.cla()
    #断面計算
    MiAvD0=[]
    for nm in range(len(MiAvC)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0) 
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)  
    #断面1計算
    MiAvD10=[]
    for nm in range(len(MiAvC)):
        MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
    MiAvD1=num.array(MiAvD10) 
    MiBvD10=[]
    for nm in range(len(MiBx)):
        MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
    MiBvD1=num.array(MiBvD10)
    MiCvD10=[]
    for nm in range(len(MiHz)):
        MiCvD10.append(c.rect(2,Tcode[0]))
    MiCvD1=num.array(MiCvD10)  
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    #中心線描画
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #分割原点
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
    ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)    
    ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
    #アニメーション描画
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="red",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output598.gif", writer="pillow")

###2分割の場合(1/2)
まさしく共役の概念が発生する瞬間。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,30,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
Tcode2=num.concatenate([Tcode[30:61], Tcode[0:29]])
#描画関数定義
def unit_cylinder(n):
    plt.cla()
    #断面計算
    MiAvD0=[]
    for nm in range(len(MiAv)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0) 
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)
    #断面計算(対蹠)
    MiDvD0=[]
    for nm in range(len(MiAv)):
        MiDvD0.append(c.rect(MiAv[nm],Tcode2[n]))
    MiDvD=num.array(MiDvD0)
    MiDvE=MiDvD[::-1]
    MiEvD0=[]
    for nm in range(len(MiBx)):
        MiEvD0.append(c.rect(MiBx[nm],Tcode2[n]))
    MiEvD=num.array(MiEvD0)
    MiFvD0=[]
    for nm in range(len(MiHz)):
        MiFvD0.append(c.rect(2,Tcode2[n]))
    MiFvD=num.array(MiFvD0)
    ucA1=num.concatenate([uc[30:61], uc[0:29]])
    #断面1計算
    MiAvD10=[]
    for nm in range(len(MiAvC)):
        MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
    MiAvD1=num.array(MiAvD10) 
    MiBvD10=[]
    for nm in range(len(MiBx)):
        MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
    MiBvD1=num.array(MiBvD10)
    MiCvD10=[]
    for nm in range(len(MiHz)):
        MiCvD10.append(c.rect(2,Tcode[0]))
    MiCvD1=num.array(MiCvD10) 
    #断面2計算
    MiAvD20=[]
    for nm in range(len(MiAvC)):
        MiAvD20.append(c.rect(MiAv[nm],Tcode[30]))
    MiAvD2=num.array(MiAvD20) 
    MiBvD20=[]
    for nm in range(len(MiBx)):
        MiBvD20.append(c.rect(MiBx[nm],Tcode[30]))
    MiBvD2=num.array(MiBvD20)
    MiCvD20=[]
    for nm in range(len(MiHz)):
        MiCvD20.append(c.rect(2,Tcode[30]))
    MiCvD2=num.array(MiCvD20) 
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    #中心線描画
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #断面1描画
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
    ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)    
    ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
    #断面2描画
    ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[-1,-1],color="purple",lw=1)
    ax.plot([0,uc[30].real],[0,uc[30].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[30].real,MiCvD2[30].real],[uc[30].imag,MiCvD2[30].imag],[0,0],color="purple",lw=1)
    ax.plot([uc[30].real,uc[30].real],[uc[30].imag,uc[30].imag],[-1,1],color="purple",lw=1)    
    ax.plot([uc[30].real,MiAvD2[30].real],[uc[30].imag,MiAvD2[30].imag],[0,MiAh[30]],color="purple",lw=1)
    ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[1,1],color="purple",lw=1)
    ax.plot([MiCvD2[30].real,MiCvD2[30].real],[MiCvD2[30].imag,MiCvD2[30].imag],[-1,1],color="purple",lw=1)
    ax.plot(MiAvD2.real,MiAvD2.imag,MiAh,color="purple",lw=1)
    ax.plot(MiBvD2.real,MiBvD2.imag,MiHz,color="blue",lw=1)
    #アニメーション描画
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="green",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #アニメーション描画(対蹠)
    ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,ucA1[n].real],[0,ucA1[n].imag],[0,0],color="blue",lw=1)
    ax.plot([ucA1[n].real,MiFvD[n].real],[ucA1[n].imag,MiFvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([ucA1[n].real,ucA1[n].real],[ucA1[n].imag,ucA1[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([ucA1[n].real,MiDvE[n].real],[ucA1[n].imag,MiDvE[n].imag],[0,MiAh[n]],color="purple",lw=1)
    ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiFvD[n].real,MiFvD[n].real],[MiFvD[n].imag,MiFvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiDvD.real,MiDvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiEvD.real,MiEvD.imag,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output604.gif", writer="pillow")

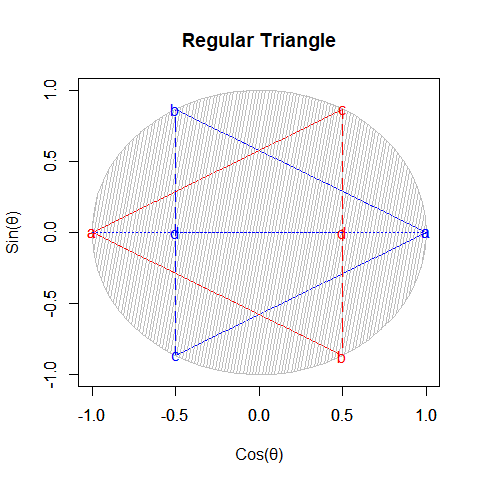
#三分割(追加分枝点2)=正三辺形の場合
奇数図形なので「対蹠それぞれを始点とする一対」が大半径に現れる。
正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

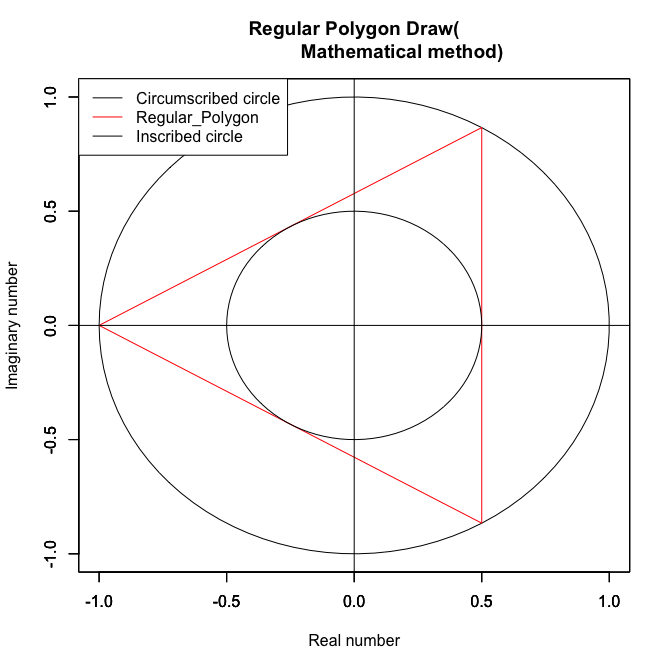
外周円を半径1とした場合の内接円の半径は0.5($\frac{1}{2}$)。同心円連鎖あり。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

小半径上での見え方(添字が負の場合は×3)

###単位トーラス上の三分割
上掲の様に「奇数図形はそれぞれの対蹠を始点とする一対」と考えると見掛け上六分割と映る。正三角形の同心円連鎖における外接円と内接円の比は、単位トーラスにおける外径と大半径の比とぴったりと重なる(どちらも$\frac{1}{2}$)。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,30,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
Tcode2=num.concatenate([Tcode[30:61], Tcode[0:29]])
#描画関数定義
def unit_cylinder(n):
    plt.cla()
    #断面計算
    MiAvD0=[]
    for nm in range(len(MiAv)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0) 
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)
    #断面計算(対蹠)
    MiDvD0=[]
    for nm in range(len(MiAv)):
        MiDvD0.append(c.rect(MiAv[nm],Tcode2[n]))
    MiDvD=num.array(MiDvD0)
    MiDvE=MiDvD[::-1]
    MiEvD0=[]
    for nm in range(len(MiBx)):
        MiEvD0.append(c.rect(MiBx[nm],Tcode2[n]))
    MiEvD=num.array(MiEvD0)
    MiFvD0=[]
    for nm in range(len(MiHz)):
        MiFvD0.append(c.rect(2,Tcode2[n]))
    MiFvD=num.array(MiFvD0)
    ucA1=num.concatenate([uc[30:61], uc[0:29]])
    #断面1計算
    MiAvD10=[]
    for nm in range(len(MiAvC)):
        MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
    MiAvD1=num.array(MiAvD10) 
    MiBvD10=[]
    for nm in range(len(MiBx)):
        MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
    MiBvD1=num.array(MiBvD10)
    MiCvD10=[]
    for nm in range(len(MiHz)):
        MiCvD10.append(c.rect(2,Tcode[0]))
    MiCvD1=num.array(MiCvD10) 
    #断面2計算
    MiAvD20=[]
    for nm in range(len(MiAvC)):
        MiAvD20.append(c.rect(MiAv[nm],Tcode[30]))
    MiAvD2=num.array(MiAvD20) 
    MiBvD20=[]
    for nm in range(len(MiBx)):
        MiBvD20.append(c.rect(MiBx[nm],Tcode[30]))
    MiBvD2=num.array(MiBvD20)
    MiCvD20=[]
    for nm in range(len(MiHz)):
        MiCvD20.append(c.rect(2,Tcode[30]))
    MiCvD2=num.array(MiCvD20) 
    #断面3計算
    MiAvD30=[]
    for nm in range(len(MiAvC)):
        MiAvD30.append(c.rect(MiAv[nm],Tcode[10]))
    MiAvD3=num.array(MiAvD30) 
    MiBvD30=[]
    for nm in range(len(MiBx)):
        MiBvD30.append(c.rect(MiBx[nm],Tcode[10]))
    MiBvD3=num.array(MiBvD30)
    MiCvD30=[]
    for nm in range(len(MiHz)):
        MiCvD30.append(c.rect(2,Tcode[10]))
    MiCvD3=num.array(MiCvD30) 
    #断面4計算
    MiAvD40=[]
    for nm in range(len(MiAvC)):
        MiAvD40.append(c.rect(MiAv[nm],Tcode[20]))
    MiAvD4=num.array(MiAvD40) 
    MiBvD40=[]
    for nm in range(len(MiBx)):
        MiBvD40.append(c.rect(MiBx[nm],Tcode[20]))
    MiBvD4=num.array(MiBvD40)
    MiCvD40=[]
    for nm in range(len(MiHz)):
        MiCvD40.append(c.rect(2,Tcode[20]))
    MiCvD4=num.array(MiCvD40) 
    #断面5計算
    MiAvD50=[]
    for nm in range(len(MiAvC)):
        MiAvD50.append(c.rect(MiAv[nm],Tcode[40]))
    MiAvD5=num.array(MiAvD20) 
    MiBvD50=[]
    for nm in range(len(MiBx)):
        MiBvD50.append(c.rect(MiBx[nm],Tcode[40]))
    MiBvD5=num.array(MiBvD50)
    MiCvD50=[]
    for nm in range(len(MiHz)):
        MiCvD50.append(c.rect(2,Tcode[40]))
    MiCvD5=num.array(MiCvD50) 
    #断面6計算
    MiAvD60=[]
    for nm in range(len(MiAvC)):
        MiAvD60.append(c.rect(MiAv[nm],Tcode[50]))
    MiAvD6=num.array(MiAvD60) 
    MiBvD60=[]
    for nm in range(len(MiBx)):
        MiBvD60.append(c.rect(MiBx[nm],Tcode[50]))
    MiBvD6=num.array(MiBvD60)
    MiCvD60=[]
    for nm in range(len(MiHz)):
        MiCvD60.append(c.rect(2,Tcode[50]))
    MiCvD6=num.array(MiCvD60) 
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    #中心線描画
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #断面1描画
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
    ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)    
    #ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
    #断面2描画
    ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[-1,-1],color="purple",lw=1)
    ax.plot([0,uc[30].real],[0,uc[30].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[30].real,MiCvD2[30].real],[uc[30].imag,MiCvD2[30].imag],[0,0],color="purple",lw=1)
    ax.plot([uc[30].real,uc[30].real],[uc[30].imag,uc[30].imag],[-1,1],color="purple",lw=1)    
    #ax.plot([uc[30].real,MiAvD2[30].real],[uc[30].imag,MiAvD2[30].imag],[0,MiAh[30]],color="purple",lw=1)
    ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[1,1],color="purple",lw=1)
    ax.plot([MiCvD2[30].real,MiCvD2[30].real],[MiCvD2[30].imag,MiCvD2[30].imag],[-1,1],color="purple",lw=1)
    ax.plot(MiAvD2.real,MiAvD2.imag,MiAh,color="purple",lw=1)
    ax.plot(MiBvD2.real,MiBvD2.imag,MiHz,color="blue",lw=1)
    #断面3描画
    ax.plot([0,MiCvD3[10].real],[0,MiCvD3[10].imag],[-1,-1],color="purple",lw=1)
    ax.plot([0,uc[10].real],[0,uc[10].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[10].real,MiCvD3[10].real],[uc[10].imag,MiCvD3[10].imag],[0,0],color="purple",lw=1)
    ax.plot([uc[10].real,uc[10].real],[uc[10].imag,uc[10].imag],[-1,1],color="purple",lw=1)    
    #ax.plot([uc[10].real,MiAvD3[10].real],[uc[10].imag,MiAvD3[10].imag],[0,MiAh[10]],color="purple",lw=1)
    ax.plot([0,MiCvD3[10].real],[0,MiCvD3[10].imag],[1,1],color="purple",lw=1)
    ax.plot([MiCvD3[10].real,MiCvD3[10].real],[MiCvD3[10].imag,MiCvD3[10].imag],[-1,1],color="purple",lw=1)
    ax.plot(MiAvD3.real,MiAvD3.imag,MiAh,color="purple",lw=1)
    ax.plot(MiBvD3.real,MiBvD3.imag,MiHz,color="blue",lw=1)
    #断面4描画
    ax.plot([0,MiCvD4[20].real],[0,MiCvD4[20].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[20].real],[0,uc[20].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[20].real,MiCvD4[20].real],[uc[20].imag,MiCvD4[20].imag],[0,0],color="green",lw=1)
    ax.plot([uc[20].real,uc[20].real],[uc[20].imag,uc[20].imag],[-1,1],color="green",lw=1)    
    #ax.plot([uc[20].real,MiAvD4[20].real],[uc[20].imag,MiAvD4[20].imag],[0,MiAh[20]],color="green",lw=1)
    ax.plot([0,MiCvD4[20].real],[0,MiCvD4[20].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD4[20].real,MiCvD4[20].real],[MiCvD4[20].imag,MiCvD4[20].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD4.real,MiAvD4.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD4.real,MiBvD4.imag,MiHz,color="blue",lw=1)
    #断面5描画
    ax.plot([0,MiCvD5[40].real],[0,MiCvD5[40].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[40].real],[0,uc[40].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[40].real,MiCvD5[40].real],[uc[40].imag,MiCvD5[40].imag],[0,0],color="green",lw=1)
    ax.plot([uc[40].real,uc[40].real],[uc[40].imag,uc[40].imag],[-1,1],color="green",lw=1)    
    #ax.plot([uc[40].real,MiAvD5[40].real],[uc[40].imag,MiAvD5[40].imag],[0,MiAh[40]],color="green",lw=1)
    ax.plot([0,MiCvD5[40].real],[0,MiCvD5[40].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD5[40].real,MiCvD5[40].real],[MiCvD5[40].imag,MiCvD5[40].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD5.real,MiAvD5.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD5.real,MiBvD5.imag,MiHz,color="blue",lw=1)
    #断面6描画
    ax.plot([0,MiCvD6[50].real],[0,MiCvD6[50].imag],[-1,-1],color="purple",lw=1)
    ax.plot([0,uc[50].real],[0,uc[50].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[50].real,MiCvD6[50].real],[uc[50].imag,MiCvD6[50].imag],[0,0],color="purple",lw=1)
    ax.plot([uc[50].real,uc[50].real],[uc[50].imag,uc[50].imag],[-1,1],color="purple",lw=1)    
    #ax.plot([uc[50].real,MiAvD6[50].real],[uc[50].imag,MiAvD6[50].imag],[0,MiAh[50]],color="purple",lw=1)
    ax.plot([0,MiCvD6[50].real],[0,MiCvD6[50].imag],[1,1],color="purple",lw=1)
    ax.plot([MiCvD6[50].real,MiCvD6[50].real],[MiCvD6[50].imag,MiCvD6[50].imag],[-1,1],color="purple",lw=1)
    ax.plot(MiAvD6.real,MiAvD6.imag,MiAh,color="purple",lw=1)
    ax.plot(MiBvD6.real,MiBvD6.imag,MiHz,color="blue",lw=1)
    #アニメーション描画
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="green",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #アニメーション描画(対蹠)
    ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,ucA1[n].real],[0,ucA1[n].imag],[0,0],color="blue",lw=1)
    ax.plot([ucA1[n].real,MiFvD[n].real],[ucA1[n].imag,MiFvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([ucA1[n].real,ucA1[n].real],[ucA1[n].imag,ucA1[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([ucA1[n].real,MiDvE[n].real],[ucA1[n].imag,MiDvE[n].imag],[0,MiAh[n]],color="purple",lw=1)
    ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiFvD[n].real,MiFvD[n].real],[MiFvD[n].imag,MiFvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiDvD.real,MiDvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiEvD.real,MiEvD.imag,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output634.gif", writer="pillow")

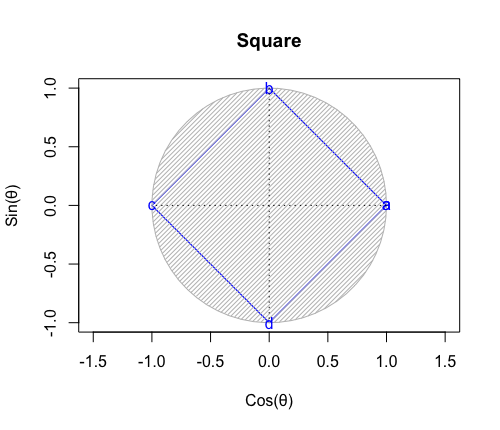
#四分割(追加分枝点3)=正方形の場合
*偶数図形なので一対の「対蹠を含む単一図形」のみが大半径に現れる。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体と正二十面体の狭間。そして正十二面体との関係について。

外周円を半径1とした場合の内接円の半径はsqrt(2)/2=0.7071068($\frac{\sqrt{2}}{2}$)。同心円連鎖あり。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

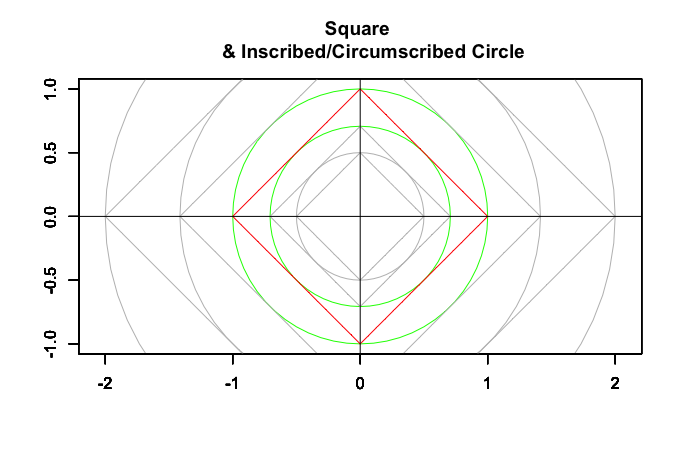
小半径上での見え方(添字が負の場合は×4)

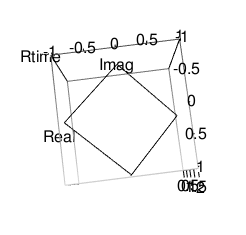
###単位トーラス上の四分割
偶素数2の導入は自明の場合として2の冪乗算の導入を意味する？

2^n(n=-\infty→0→+\infty)=(2^{-\infty}=\frac{1}{\infty}=0,…,2^{-2}=\frac{1}{2^2}=\frac{1}{4},…,2^{-1}=\frac{1}{2},…,2^0=\frac{2}{2}=1,…,2^1=2,…,2^2=4,…,2^{+\infty}=\infty)

【Rで九九】どうして36個の数字しか使われないのか？
【数理考古学】冪乗算の微積分

• 幾何学的には二分割(二倍)をさらに二分割($\frac{1}{2}$)した結果とも見て取れる。
  
  
  

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,30,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
Tcode2=num.concatenate([Tcode[30:61], Tcode[0:29]])
Tcode3=num.concatenate([Tcode[15:61], Tcode[0:14]])
Tcode4=num.concatenate([Tcode[45:61], Tcode[0:44]])
#描画関数定義
def unit_cylinder(n):
    plt.cla()
    #断面計算(元)
    MiAvD0=[]
    for nm in range(len(MiAv)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0) 
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)
    #断面計算(対蹠)
    MiDvD0=[]
    for nm in range(len(MiAv)):
        MiDvD0.append(c.rect(MiAv[nm],Tcode2[n]))
    MiDvD=num.array(MiDvD0)
    MiDvE=MiDvD[::-1]
    MiEvD0=[]
    for nm in range(len(MiBx)):
        MiEvD0.append(c.rect(MiBx[nm],Tcode2[n]))
    MiEvD=num.array(MiEvD0)
    MiFvD0=[]
    for nm in range(len(MiHz)):
        MiFvD0.append(c.rect(2,Tcode2[n]))
    MiFvD=num.array(MiFvD0)
    ucA1=num.concatenate([uc[30:61], uc[0:29]])
    #断面計算(交代)
    MiAvDA0=[]
    for nm in range(len(MiAv)):
        MiAvDA0.append(c.rect(MiAv[nm],Tcode3[n]))
    MiAvDA=num.array(MiAvDA0) 
    MiBvDA0=[]
    for nm in range(len(MiBx)):
        MiBvDA0.append(c.rect(MiBx[nm],Tcode3[n]))
    MiBvDA=num.array(MiBvDA0)
    MiCvDA0=[]
    for nm in range(len(MiHz)):
        MiCvDA0.append(c.rect(2,Tcode3[n]))
    MiCvDA=num.array(MiCvDA0)
    ucAA=num.concatenate([uc[15:61], uc[0:14]])
    #断面計算(交代の対蹠)
    MiDvDB0=[]
    for nm in range(len(MiAv)):
        MiDvDB0.append(c.rect(MiAv[nm],Tcode4[n]))
    MiDvDB=num.array(MiDvDB0)
    MiDvEB=MiDvDB[::-1]
    MiEvDB0=[]
    for nm in range(len(MiBx)):
        MiEvDB0.append(c.rect(MiBx[nm],Tcode4[n]))
    MiEvDB=num.array(MiEvDB0)
    MiFvDB0=[]
    for nm in range(len(MiHz)):
        MiFvDB0.append(c.rect(2,Tcode4[n]))
    MiFvDB=num.array(MiFvDB0)
    ucAB=num.concatenate([uc[45:61], uc[0:44]])

    #断面1計算
    MiAvD10=[]
    for nm in range(len(MiAvC)):
        MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
    MiAvD1=num.array(MiAvD10) 
    MiBvD10=[]
    for nm in range(len(MiBx)):
        MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
    MiBvD1=num.array(MiBvD10)
    MiCvD10=[]
    for nm in range(len(MiHz)):
        MiCvD10.append(c.rect(2,Tcode[0]))
    MiCvD1=num.array(MiCvD10) 
    #断面2計算
    MiAvD20=[]
    for nm in range(len(MiAvC)):
        MiAvD20.append(c.rect(MiAv[nm],Tcode[30]))
    MiAvD2=num.array(MiAvD20) 
    MiBvD20=[]
    for nm in range(len(MiBx)):
        MiBvD20.append(c.rect(MiBx[nm],Tcode[30]))
    MiBvD2=num.array(MiBvD20)
    MiCvD20=[]
    for nm in range(len(MiHz)):
        MiCvD20.append(c.rect(2,Tcode[30]))
    MiCvD2=num.array(MiCvD20) 
    #断面3計算
    MiAvD30=[]
    for nm in range(len(MiAvC)):
        MiAvD30.append(c.rect(MiAv[nm],Tcode[15]))
    MiAvD3=num.array(MiAvD30) 
    MiBvD30=[]
    for nm in range(len(MiBx)):
        MiBvD30.append(c.rect(MiBx[nm],Tcode[15]))
    MiBvD3=num.array(MiBvD30)
    MiCvD30=[]
    for nm in range(len(MiHz)):
        MiCvD30.append(c.rect(2,Tcode[15]))
    MiCvD3=num.array(MiCvD30) 
    #断面4計算
    MiAvD40=[]
    for nm in range(len(MiAvC)):
        MiAvD40.append(c.rect(MiAv[nm],Tcode[45]))
    MiAvD4=num.array(MiAvD40) 
    MiBvD40=[]
    for nm in range(len(MiBx)):
        MiBvD40.append(c.rect(MiBx[nm],Tcode[45]))
    MiBvD4=num.array(MiBvD40)
    MiCvD40=[]
    for nm in range(len(MiHz)):
        MiCvD40.append(c.rect(2,Tcode[45]))
    MiCvD4=num.array(MiCvD40) 
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    #中心線描画
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #断面1描画
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
    ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)    
    ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
    #断面2描画
    ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[-1,-1],color="purple",lw=1)
    ax.plot([0,uc[30].real],[0,uc[30].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[30].real,MiCvD2[30].real],[uc[30].imag,MiCvD2[30].imag],[0,0],color="purple",lw=1)
    ax.plot([uc[30].real,uc[30].real],[uc[30].imag,uc[30].imag],[-1,1],color="purple",lw=1)    
    ax.plot([uc[30].real,MiAvD2[30].real],[uc[30].imag,MiAvD2[30].imag],[0,MiAh[30]],color="purple",lw=1)
    ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[1,1],color="purple",lw=1)
    ax.plot([MiCvD2[30].real,MiCvD2[30].real],[MiCvD2[30].imag,MiCvD2[30].imag],[-1,1],color="purple",lw=1)
    ax.plot(MiAvD2.real,MiAvD2.imag,MiAh,color="purple",lw=1)
    ax.plot(MiBvD2.real,MiBvD2.imag,MiHz,color="blue",lw=1)
    #断面3描画
    ax.plot([0,MiCvD3[15].real],[0,MiCvD3[15].imag],[-1,-1],color="steelblue",lw=1)
    ax.plot([0,uc[15].real],[0,uc[15].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[15].real,MiCvD3[15].real],[uc[15].imag,MiCvD3[15].imag],[0,0],color="steelblue",lw=1)
    ax.plot([uc[15].real,uc[15].real],[uc[15].imag,uc[15].imag],[-1,1],color="steelblue",lw=1)    
    ax.plot([uc[15].real,MiAvD3[15].real],[uc[15].imag,MiAvD3[15].imag],[0,MiAh[15]],color="steelblue",lw=1)
    ax.plot([0,MiCvD3[15].real],[0,MiCvD3[15].imag],[1,1],color="steelblue",lw=1)
    ax.plot([MiCvD3[15].real,MiCvD3[15].real],[MiCvD3[15].imag,MiCvD3[15].imag],[-1,1],color="steelblue",lw=1)
    ax.plot(MiAvD3.real,MiAvD3.imag,MiAh,color="steelblue",lw=1)
    ax.plot(MiBvD3.real,MiBvD3.imag,MiHz,color="blue",lw=1)
    #断面4描画
    ax.plot([0,MiCvD4[45].real],[0,MiCvD4[45].imag],[-1,-1],color="salmon",lw=1)
    ax.plot([0,uc[45].real],[0,uc[45].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[45].real,MiCvD4[45].real],[uc[45].imag,MiCvD4[45].imag],[0,0],color="salmon",lw=1)
    ax.plot([uc[45].real,uc[45].real],[uc[45].imag,uc[45].imag],[-1,1],color="salmon",lw=1)    
    ax.plot([uc[45].real,MiAvD4[45].real],[uc[45].imag,MiAvD4[45].imag],[0,MiAh[45]],color="salmon",lw=1)
    ax.plot([0,MiCvD4[45].real],[0,MiCvD4[45].imag],[1,1],color="salmon",lw=1)
    ax.plot([MiCvD4[45].real,MiCvD4[45].real],[MiCvD4[45].imag,MiCvD4[45].imag],[-1,1],color="salmon",lw=1)
    ax.plot(MiAvD4.real,MiAvD4.imag,MiAh,color="salmon",lw=1)
    ax.plot(MiBvD4.real,MiBvD4.imag,MiHz,color="blue",lw=1)
    #アニメーション描画
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="green",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    #ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #アニメーション描画(対蹠)
    ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,ucA1[n].real],[0,ucA1[n].imag],[0,0],color="blue",lw=1)
    ax.plot([ucA1[n].real,MiFvD[n].real],[ucA1[n].imag,MiFvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([ucA1[n].real,ucA1[n].real],[ucA1[n].imag,ucA1[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([ucA1[n].real,MiDvE[n].real],[ucA1[n].imag,MiDvE[n].imag],[0,MiAh[n]],color="purple",lw=1)
    ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiFvD[n].real,MiFvD[n].real],[MiFvD[n].imag,MiFvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiDvD.real,MiDvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiEvD.real,MiEvD.imag,MiHz,color="blue",lw=1)
    #アニメーション描画(交代)
    ax.plot([0,MiCvDA[n].real],[0,MiCvDA[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,ucAA[n].real],[0,ucAA[n].imag],[0,0],color="blue",lw=1)
    ax.plot([ucAA[n].real,MiCvDA[n].real],[ucAA[n].imag,MiCvDA[n].imag],[0,0],color="black",lw=1)
    ax.plot([ucAA[n].real,ucAA[n].real],[ucAA[n].imag,ucAA[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([ucAA[n].real,MiAvDA[n].real],[ucAA[n].imag,MiAvDA[n].imag],[0,MiAh[n]],color="steelblue",lw=1)
    ax.plot([0,MiCvDA[n].real],[0,MiCvDA[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvDA[n].real,MiCvDA[n].real],[MiCvDA[n].imag,MiCvDA[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvDA.real,MiAvDA.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvDA.real,MiBvDA.imag,MiHz,color="blue",lw=1)
    #アニメーション描画(交代の対蹠)
    ax.plot([0,MiFvDB[n].real],[0,MiFvDB[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,ucAB[n].real],[0,ucAB[n].imag],[0,0],color="blue",lw=1)
    ax.plot([ucAB[n].real,MiFvDB[n].real],[ucAB[n].imag,MiFvDB[n].imag],[0,0],color="black",lw=1)
    ax.plot([ucAB[n].real,ucAB[n].real],[ucAB[n].imag,ucAB[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([ucAB[n].real,MiDvEB[n].real],[ucAB[n].imag,MiDvEB[n].imag],[0,MiAh[n]],color="salmon",lw=1)
    ax.plot([0,MiFvDB[n].real],[0,MiFvDB[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiFvDB[n].real,MiFvDB[n].real],[MiFvDB[n].imag,MiFvDB[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiDvDB.real,MiDvDB.imag,MiAh,color="red",lw=1)
    ax.plot(MiEvDB.real,MiEvDB.imag,MiHz,color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output612.gif", writer="pillow")

さらに次段階でZ軸方向への座標軸を追加すると(幾何学的には「二枚の正方形を垂直に交わらせる」といった考え方もする)、トーラス状態を終えて三次元デカルト座標系、あるいは正八面体の幾何学に到達しそうです。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

#五分割(追加分枝点4)=正五辺形の場合
奇数図形なので「対蹠それぞれを始点とする一対」が大半径に現れる。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体と正二十面体の狭間。そして正十二面体との関係について。

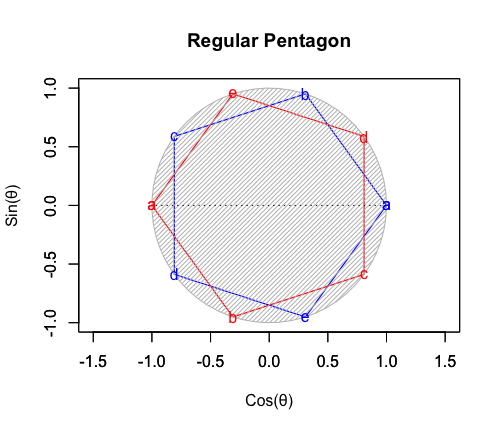
外周円を半径1とした場合の内接円の半径は0.8090168。同心円連鎖なし。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

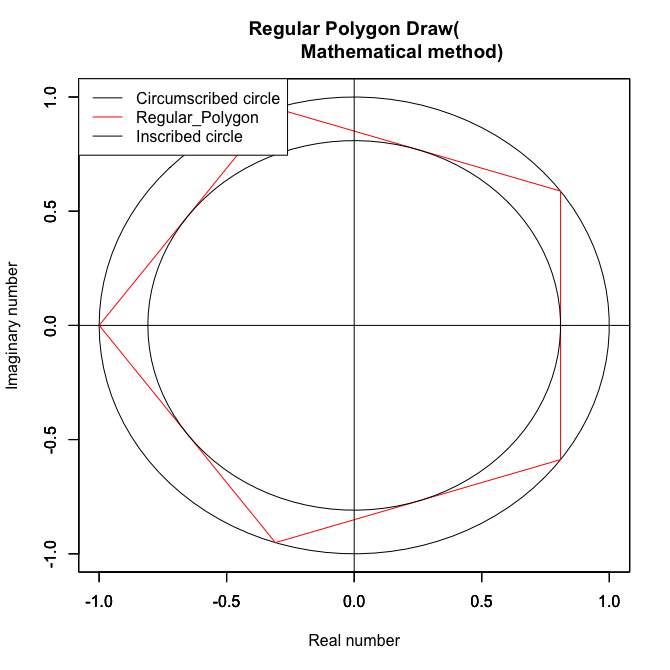
小半径上での見え方(添字が負の場合は×5)

#六分割(追加分枝点5)=正六辺形の場合
*偶数図形なので「一対の対蹠を含む単一図形」のみが大半径に現れる。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体と正二十面体の狭間。そして正十二面体との関係について。

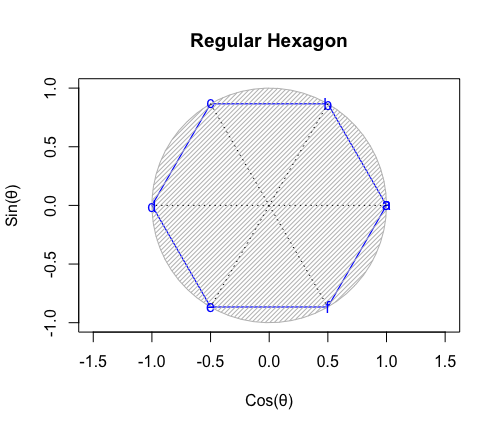
外周円を半径1とした場合の内接円の半径は0.8660254。同心円連鎖なし。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

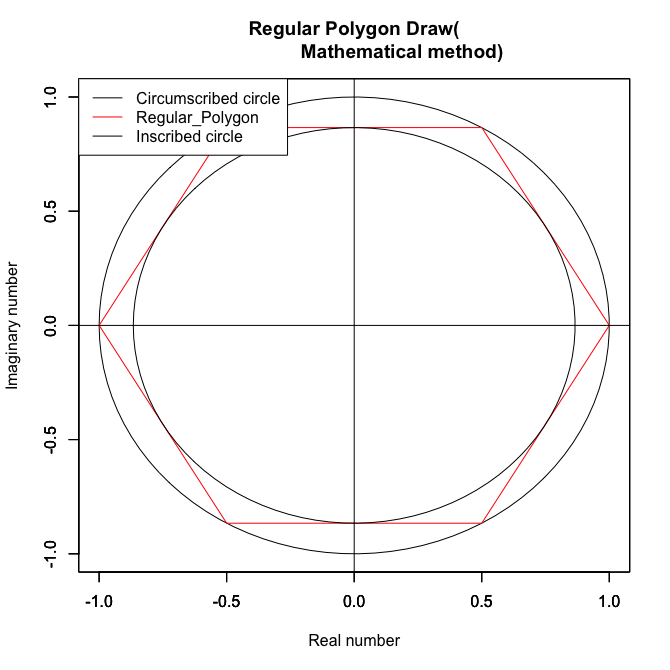
小半径上での見え方(添字が負の場合は×5)

#「ティンダロスの猟犬」問題との関係?
上掲の関係がなんとなくながらオイラーの公式（Eulerian Formula）$Cos(θ)+Sin(θ)i$の一般形たる以下の式の関連を期待させますね。

Cos(θ)+Cos(θ-\frac{π}{NoS})i(NoS=Number of Sides)

【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

【Rで球面幾何学】二辺形と一辺形？
NoS=1→8の場合(NpS=2の場合を検出)

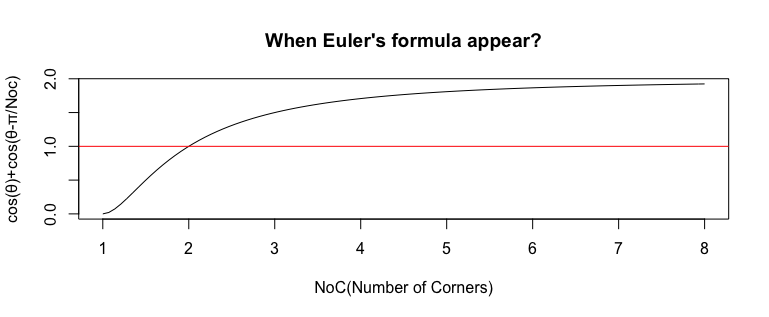
NoS=1→0の場合(NpS=$\frac{2}{3},\frac{2}{5},\frac{2}{7},…$と$\frac{2}{2n+1}$の場合を検出)

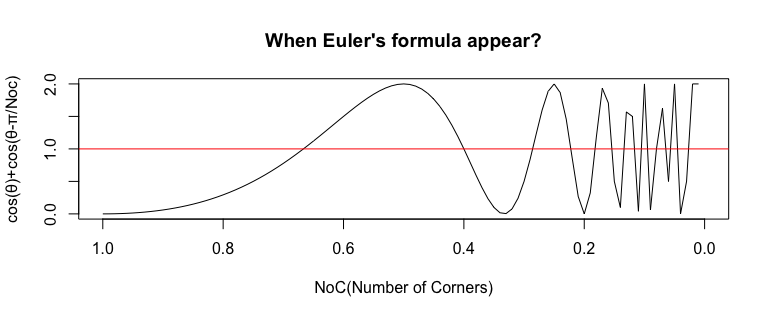
複素平面上での表現(NoS=1の場合を含む周期の下限)

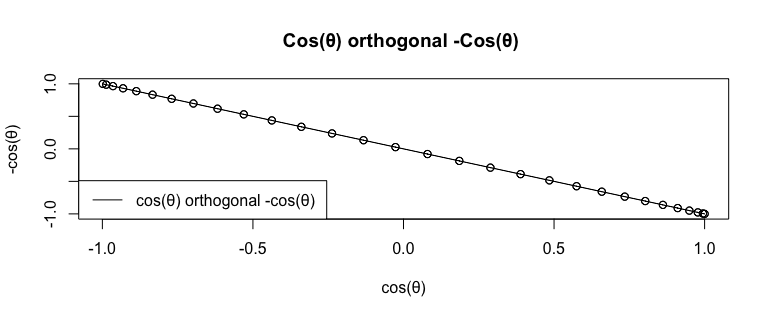
複素平面上での表現(NoS=2の場合を含む周期の中央値)

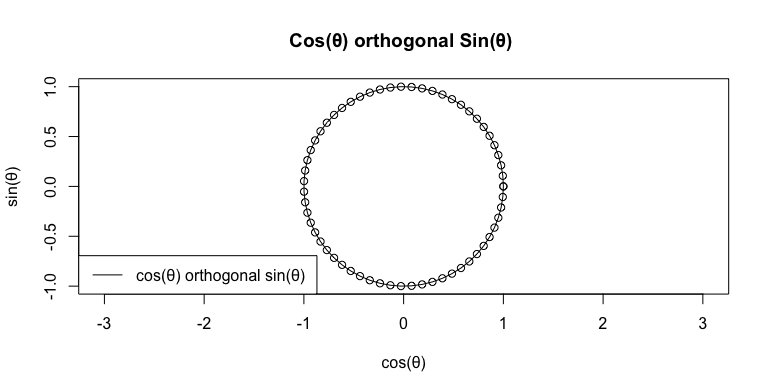
複素平面上での表現(NoS=∞の場合を含む周期の上限)

複素平面上での表現(NoS=1→∞)…あまりに収束が遅いので途中で加速。

複素平面上での表現(NoS=1→0)…0に近くほど超新星(Pulsar)の様に加速。

そもそも未だに何を検出してるかすら判らない謎の式という…(どうやら「直交=内積0」概念に対応する様だが$\frac{2}{2n+1}$角形におけるそれって何？)
【無限遠点を巡る数理】「ティンダロスの猟犬問題」を世に解き放つ。
【用語集】「ティンダロスの猟犬」について。

#「40周期複素関数」問題との関係?
「円に内接/外接する多角形」といえば、以下の数理も偶然発見しつつそれ以降放置を決め込んできたのです。正N角形(ただしNは整数とは限らない)という辺りで上掲の「ティンダロスの猟犬問題」と関連してくる？
【無限遠点を巡る数理】オイラー座標系②複素等比数列による整数概念の再構築。



はてさて一体どこから着手すれば良いやら…

#「位相が等差数列である三角関数の和」との関係?
ついでにこれもあげておきましょう。
チェビシェフ多項式 | 高校数学の美しい物語

位相が等差数列である三角関数の和

cos(π)=-1\\
cos(\frac{π}{2})=0\\
cos(\frac{π}{3})=\frac{1}{2}\\
cos(\frac{π}{5})+cos(\frac{3π}{5})=\frac{1}{2}\\
cos(\frac{π}{7})+cos(\frac{3π}{7})+cos(\frac{5π}{7})=\frac{1}{2}\\
cos(\frac{π}{9})+cos(\frac{3π}{9})+cos(\frac{5π}{9})+cos(\frac{7π}{9})=\frac{1}{2}\\
cos(\frac{π}{11})+cos(\frac{3π}{11})+cos(\frac{5π}{11})+cos(\frac{7π}{11})+cos(\frac{9π}{11})=\frac{1}{2}

そして素数でない$cos(\frac{9π}{11})$を除いた計算結果は

cos(\frac{π}{11})+cos(\frac{3π}{11})+cos(\frac{5π}{11})+cos(\frac{7π}{11})=1.341254

これは黄金比(10進法で1.618033 988749…)を6進法(1.341254 554353 4312…)で表した結果に等しい。

Rによる検算結果

> cos(pi)
[1] -1
> round(cos(pi/2),digit=8)
[1] 0
> cos(pi/3)
[1] 0.5
> cos(pi/5)+cos((3*pi)/5)
[1] 0.5
> cos(pi/7)+cos((3*pi)/7)+cos((5*pi)/7)
[1] 0.5
> cos(pi/9)+cos((3*pi)/9)+cos((5*pi)/9)+cos((7*pi)/9)
[1] 0.5 
cos(pi/11)+cos((3*pi)/11)+cos((5*pi)/11)+cos((7*pi)/11)+cos((9*pi)/11)
[1] 0.5
> cos(pi/11)+cos((3*pi)/11)+cos((5*pi)/11)+cos((7*pi)/11)
[1] 1.341254

• ライプニッツ=グレゴリー級数との関係も興味深い。

ライプニッツ級数(Leibniz series,1674年)

\sum_{n}^{\infty}\frac{-1^n}{2n+1}=\frac{π}{4}

グレゴリー級数(Gregory series, 1671年)

\sum_{n}^{\infty}\frac{-1^n}{2n+1}x^{2n+1}=\frac{π}{4}

x=1の時、ライプニッツ級数と一致する。
【数理考古学】とある円周率への挑戦？

何か関係が出てきそうな気がするのですが…現段階では判断が下せません。
・
#とりあえず以下続報…
随時pythonで実装していく予定。そんな感じで以下続報…