【無限遠点を巡る数理】無限直線(Infinity Line)/無限円(Infinity Circle)/無限球面(Infinity Sphere)そして無限トーラス(Infinity Torus)? - Qiita
この投稿において私はやっと無限直線(Infinity/Unlimited Line)/無限円(Infinity/Unlimited Circle)/無限球面(Infinity/Unlimited Sphere)によって構成される原始座標系(Primitive Coordinate System)の世界観に「オイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iおよびその一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)」概念を不可逆的な形で組み込む事に成功しました。しかし同時にオイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iが成立するNoS=2以下の展開を切り捨てるという苦渋の選択を迫られたのです。
【Rで球面幾何学】二辺形(Bilateral)と一辺形(One Side)? - Qiita
辺数の判別式でもある数式Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)は、角度範囲としてθ=0→πの周期を与えると1辺形(One Side)をその答えとして返します。そしてそれ以上の辺数では(Cos(θ)+Sin(θ)i概念が成立する)二辺形(Bilateral)しか満たさない直交条件NoS=2/(2N+1)を満たす2/3辺形、2/5辺形、2/7辺形などが出現周期を短縮しつつ辺数0に向けて顕現し続けるのです。
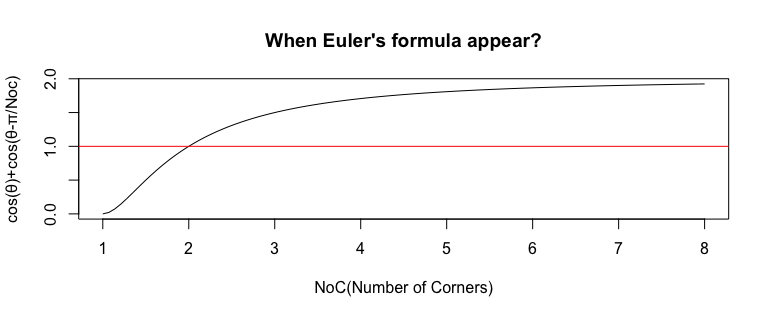
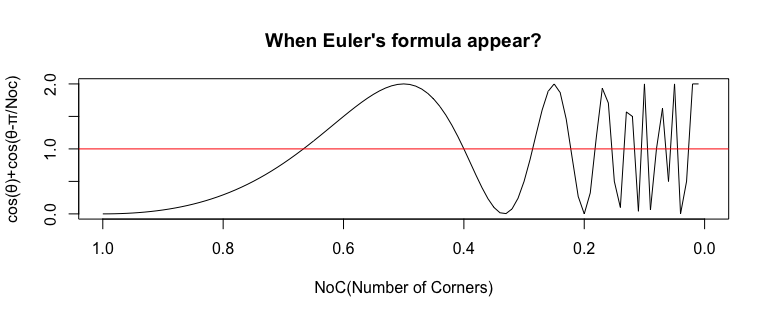
アニメーション化してみましょう。予測通り「(直交度合いを意味する)円盤が回転速度を上げながら旋回している」光景が現出しました。この数式、おそらく相関係数(Correlation Coefficient)の概念とも密接な関係がある筈なのに、何たる暴虐無尽な振る舞い!!
これが私を昨年末から悩ませてきた仮称「ティンダロスの猟犬(The Hounds of Tindalos)問題」。しかし私のSAN値にも限界があるので、この辺りで公表の運びとさせて頂きます。
SAN値 (さんち)とは【ピクシブ百科事典】
「僕には時間がないんだ (je n'ai pas le temps)。後は誰かが勝手にどうぞ!!」
