とりあえず距離概念(Distance Comcept)が観測原点(Origin of Observation)0=Xn(n=1→Inf){0,0,0,…,0}と観測対象(Target of Observation)の極限(Limit)たる無限遠点(Inf(inity))Inf=Yn(n=1→Inf){Inf,Inf,Inf,…,Inf}を結ぶ距離(Distance){0,Inf}間しか存在しか存在しない最も原始的な観測環境(Most Primitive Observation Environment)から出発します。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
無限直線(Infinity Line)/無限円(Infinity Circle)/無限球面(Infinity Sphere)はアーベル群(Abelian Group)/可換群(Commutative Group)に分類される線群(Circle Line)/円群(Circle Group)/球面群(Sphere Group)でもある?
ここから観測原点(Origin of Observation)0を中心(Cnter)に据え、無限直線(Infinity line)){0,Inf}を半径(Radius)とする無限円(Infinity Circle)sqrt(x^2+y^2)/無限球面(Infinity Sphere)sqrt(x^2+y^2+z^2)をイメージするのは容易です。
無限円(Infinity Circle)/無限球面(Infinity Sphere)

# CVCM=等速円運動(Constant Velocity Circular Motion)
# Radian=角度(60分割)
CVCM<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),main="Infinity Circle",xlab="cos(θ)",ylab="sin(θ)")
# 塗りつぶし(円)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(0,0,"(0,0,0,…)",col=rgb(0,0,1))
text(cx[Radian],cy[Radian],"(Inf,Inf,Inf,…)",col=rgb(0,0,1))
segments(cx[Radian],cy[Radian],0,0,col=rgb(0,0,1))
# 凡例
legend("bottomright", legend=c("side=2π*Inf","radius=Inf"), lty=c(1,1), col=c(rgb(0,1,0),rgb(0,0,1)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CVCM(i)
}
}, interval = 0.1, movie.name = "CVCM02.gif")
ところで群論(Group Theory)において群概念(Group Concept)の成立条件を満たすには単位元(Identity Element)と逆元(Inverse Element)を定める必要があり、半径(Radius){0,Inf}にとってそれは観測原点(Origin of Observation)0を単位元に定め、観測対象(Target of Observation)Infの逆元-Infの概念を追加する、すなわち対蹠(Antipode){0,-Inf}概念を追加して直径(Diameter){-Inf,0,Inf}を定めるプロセスに他なりません。
無限円(Infinity Circle)/無限球面(Infinity Sphere)

# CVCM=等速円運動(Constant Velocity Circular Motion)
# Radian=角度(60分割)
CVCM<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),main="Infinity Circle",xlab="cos(θ)",ylab="sin(θ)")
# 塗りつぶし(円)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(0,0,"(0,0,0,…)",col=rgb(1,0,0))
text(cx[Radian],cy[Radian],"(Inf,Inf,Inf,…)",col=rgb(1,0,0))
segments(cx[Radian],cy[Radian],0,0,col=rgb(1,0,0))
# 対蹠の設定
text(-cx[Radian],-cy[Radian],"(-Inf,-Inf,-Inf,…)",col=rgb(0,0,1))
segments(-cx[Radian],-cy[Radian],0,0,col=rgb(0,0,1))
# 凡例
legend("bottomright", legend=c("side=2π*Inf","radius=Inf"), lty=c(1,1), col=c(rgb(0,1,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CVCM(i)
}
}, interval = 0.1, movie.name = "CVCM03.gif")
実際に群概念が成立するにはさらに任意の元(Element)g,h,kについて二項演算(Binary Operation)○の結合則(Associative law)(g○h)○k)=g○(h○k)が成立する必要があり、さらに交換則(Commutative law)g○h=h○gも成立するなら、その群はアーベル群(Abelian Group)/可換群(Commutative Group)と呼ばれます。
交換法則、結合法則、分配法則
最も原始的な観測環境(Most Primitive Observation Environment)における二項演算(Binary Operation)の四則(六則)演算の結果
- 加法の極限(Limit of Addition)Inf(inity)+Inf(inity)=Inf(inity)
- 減法の極限(Limit of Subtraction)Inf(inity)-Inf(inity)=0(加法単位元)
- 乗法の極限(Limit of Multiplicative)Inf(inity)*Inf(inity)=Inf(inity)
- 除法の極限(Limit of Division)Inf(inity)/Inf(inity)=1(乗法単位元)
- 冪乗の極限(Limit of Exponentiation)Inf(inity)^Inf(inity)=Inf(inity)
- 冪根の極限(Root of Inf(inity))Inf(inity)^(1/Inf(inity))=1(乗法単位元)
統計言語Rの標準ライブラリによる計算結果
# 標準ライブラリにおける無限遠点(Inf(inity))の六則演算
# 加法の極限(Limit of Addition)
# Inf(inity)+Inf(inity)=Inf(inity)
> Inf+Inf
[1] Inf
# 減法の極限(Limit of Subtraction)
# Inf(inity)-Inf(inity)=0
> Inf-Inf
[1] NaN
# 乗法の極限(Limit of Multiplicative)
# Inf(inity)-Inf(inity)=Inf(inity)
> Inf*Inf
[1] Inf
# 除法の極限(Limit of Division)
# Inf(inity)/Inf(inity)=1
> Inf/Inf
[1] NaN
# 冪乗の極限(Limit of Exponentiation)
# Inf(inity)^Inf(inity)=Inf(inity)
> Inf^Inf
[1] Inf
# 冪根の極限(Root of Inf(inity))
# Inf(inity)^(1/Inf(inity))=1
> Inf^(1/Inf)
[1] 1
代数計算ライブラリYacasにおける計算結果
# 代数計算ライブラリYacasにおける無限遠点(Inf(inity))の六則演算
library(Ryacas)
# 加法の極限(Limit of Addition)
# Inf(inity)+Inf(inity)=Inf(inity)
> yac("Limit(x,Infinity) Infinity+Infinity")
[1] "Infinity"
# 減法の極限(Limit of Subtraction)
# Inf(inity)-Inf(inity)=0
> yac("Limit(x,Infinity) Infinity-Infinity")
[1] "Undefined"
# 乗法の極限(Limit of Multiplicative)
# Inf(inity)*Inf(inity)=Inf(inity)
> yac("Limit(x,Infinity) Infinity*Infinity")
[1] "Infinity"
# 除法の極限(Limit of Division)
# Inf(inity)/Inf(inity)=1
> yac("Limit(x,Infinity) Infinity/Infinity")
[1] "Undefined"
# 冪乗の極限(Limit of Exponentiation)
# Inf(inity)^Inf(inity)=Inf(inity)
> yac("Limit(x,Infinity) Infinity^Infinity")
[1] "Infinity"
# 冪根の極限(Root of Inf(inity))
# Inf(inity)^(1/Inf(inity))=1
> yac("Limit(x,Infinity) Infinity^(1/Infinity)")
[1] "Undefined"
加法における結合則(Associative law of Addition)と加法における交換則(Commutative law of Addition)は共に成立(実は加法単位元0の加算は無意味)。
- (-Inf+Inf)+0=0
- -Inf+(Inf+0)=0
- (0-Inf)+Inf=0
- 0+(-Inf+Inf)=0
- (-Inf+0)+Inf=0
- -Inf+(0+Inf)=0
- (Inf-Inf)+0=0
- -Inf+(-Inf+0)=0
- (0+Inf)-Inf=0
- 0+(Inf-Inf)=0
- (Inf+0)-Inf=0
- -Inf+(0-Inf)=0
実際には以下の3則の組み合わせに単純化出来そうである。
- Inf+Inf=2Inf=Inf
- Inf+(-Inf)=(-Inf)+Inf=0
- 0+0=0
統計言語Rの標準ライブラリによる計算結果
> Inf+Inf
[1] Inf
> Inf+(-Inf)
[1] NaN
> (-Inf)+Inf
[1] NaN
減法における結合法則(Associative law of Subtraction)も減法における交換則(Commutative law of Subtraction)も不成立(実は加法単位元0の減算は無意味)
- (-Inf-Inf)-0=-2*Inf=-Inf
- -Inf-(Inf-0)=-2*Inf=-Inf
- (0-(-Inf))-Inf=0
- 0-(-Inf-Inf)=2*Inf=Inf
- (-Inf-0)-Inf=-2*Inf=-Inf
- -Inf-(0-Inf)=-2*Inf=-Inf
- (Inf-Inf)+0=0
- -Inf-(-Inf-0)=2*Inf=Inf
- (0-Inf)-(-Inf)=0
- 0-(Inf-(-Inf))=0
- (Inf-0)-(-Inf)=2*Inf=Inf
- Inf-(0-(-Inf))=0
実際には以下の3則の組み合わせに単純化出来そうである。
- -Inf-Inf=-2Inf=-Inf
- Inf-Inf=-Inf+Inf=0
- 0+0=0
統計言語Rの標準ライブラリによる計算結果
> Inf-0
[1] Inf
> 0-Inf
[1] -Inf
> Inf-Inf
[1] NaN
> -Inf+Inf
[1] NaN
乗法における結合法則(Associative law of Multiplicative)と乗法における交換則(Commutative law of Multiplicative)は共に成立。
- (-Inf*Inf)0=-Inf^20=0
- -Inf*(Inf0)=-Inf0=0
- (0*(-Inf))Inf=0Inf=0
- 0*(-InfInf)=-Inf^20=0
- (-Inf*0)Inf=0Inf=0
- -Inf*(0*-Inf)=-Inf*0=0
- (Inf*-Inf)0=-Inf^20=0
- -Inf*(-Inf0)=Inf0=0
- (0Inf)(-Inf)=0*(-Inf)=0
- 0*(Inf*(-Inf))=0
- (Inf0)(-Inf)=0*(-Inf)=0
- Inf*(0*(-Inf))=Inf*0=0
実際には以下の5則の組み合わせに単純化出来そうである。
- Inf*Inf=Inf^2=Inf
- Inf*(-Inf)=-Inf*Inf=(-Inf)^2=-Inf
- (-Inf)*(-Inf)=Inf^2=Inf
- ±Inf0=0±Inf=0
- 0*0=0
統計言語Rの標準ライブラリによる計算結果
> Inf*Inf
[1] Inf
> Inf^2
[1] Inf
> Inf*(-Inf)
[1] -Inf
> (-Inf)*Inf
[1] -Inf
> (-Inf)*(-Inf)
[1] Inf
> 0*Inf
[1] NaN
> 0*(-Inf)
[1] NaN
> Inf*0
[1] NaN
> -Inf*0
[1] NaN
除法における結合法則(Associative law of Division)と除法における交換則(Commutative law of Multiplicative)は不成立(ここではとりあえず0による割り算を不可能ではなくInf/0=Inf/(1/Inf)=Inf^2=Inf,1/0=1/(1/Inf)=Infといった具合に柔軟に考える)
- (-Inf/Inf)/0=-1/0=-Inf
- -Inf/(Inf/0)=-Inf/0=-Inf
- (0/(-Inf))/Inf=0/Inf=0
- 0/(-Inf/Inf)=-0/1=0
- (-Inf/0)/Inf=-Inf/Inf=-1
- -Inf/(0/-Inf)=-Inf/Inf=-1
- (Inf/-Inf)/0=-1/0=-Inf
- -Inf/(-Inf/0)=-Inf/Inf=-1
- (0/Inf)/-Inf=0/-Inf=0
- 0/(Inf/-Inf)=0
- (Inf/0)/(-Inf)=-Inf^2/Inf=-Inf
- Inf/(0/(-Inf))=-Inf/0=Inf^2=Inf
実際には以下の7則の組み合わせに単純化出来そうである。
- Inf/Inf=1
- Inf/(-Inf)=-Inf/Inf=-1
- 0/±Inf=0
- 0/±1=0
- ±Inf/0=±Inf^2=Inf
- ±1/0=±Inf
- 0/0=0
統計言語Rの標準ライブラリによる計算結果
> Inf/Inf
[1] NaN
> Inf/(-Inf)
[1] NaN
> -Inf/Inf
[1] NaN
> 0/Inf
[1] 0
> 0/-Inf
[1] 0
> 0/1
[1] 0
> 0/-1
[1] 0
> Inf/0
[1] Inf
> -Inf/0
[1] -Inf
> 1/0
[1] Inf
> -1/0
[1] -Inf
> 0/0
[1] NaN
上掲の内容についてさらなる検証が必要なのは明らかですが(とりあえず原則として問題となるのは方向だけで、入力としては{-Inf,0,Inf},出力としては{-Inf,0,1,Inf}のみとなる事までしか指摘出来ない)、ここで成立を確認したかったのは以下のみ。
- 加法における結合則(Associative law of Addition)
- 加法における交換則(Commutative law of Addition)
- 乗法における結合法則(Associative law of Multiplicative)
- 乗法における交換則(Commutative law of Multiplicative)
全て確認できましたので、以降はここで取り上げた無限直線(Infinity Line)/無限円(Infinity Circle)/無限球面(Infinity Sphere)についてアーベル群(Abelian Group)/可換群(Commutative Group)に分類される線群(Circle Line)/円群(Circle Group)/球面群(Sphere Group)でもある可能性も視野に入れて話を進めていきます。
正直群論についての知識が皆無なので、その事が何を意味しているのか全く分かっていないのですが(だから上掲の内容にはとんでも無い誤謬が含まれてる可能性がある。そもそも「無限遠点を巡る四則演算」も教科書的内容から随分と解離してしまっている)、とにかく半径(Radius)と直径(Diameter)の関係、加法単位元(Additive Identity)0や乗法単位元(Multiplicative Identity)1の概念を上手く全体構造に組み込む方法を他に思いつけなかったのでした。実際には「加法単位元と乗法単位元の両方を備えたら、それは環(Ring)なのでは?」という観点や以下の様な話もあり、まだまだ慎重に検討を続ける必要がある様です。
環 (数学) - Wikipedia
「単位元は存在するなら1つだけ」の証明
無限円(Infinity Circle)/無限球面(Infinity Sphere)そして無限トーラス(Infinity Torus)概念の追加。
それにつけても以下が成立する無限直線(Infinity Line)/無限円(Infinity Circle)/無限球面(Infinity Sphere)の世界のN次元的多層性は強烈です。
- Inf(inity)+Inf(inity)=2*Inf(inity)=Inf(inity)
- Inf(inity)*Inf(inity)=Inf(inity)^2=Inf(inity)
要するに半径Infの円/球面を中心に{半径2Infの円/球面,半径4Infの円/球面,半径8Infの円/球面,…,半径Infの円/球面}と{半径Inf/2の円/球面,半径Inf/4の円/球面,半径Inf/8の円/球面,…,半径Infの円/球面が}無限に重なっていて、そこに織り込まれた「図形の1/2ずつのズレ」なる概念こそが「周期の偶奇性」概念の大源流となる訳です。
【初心者向け】偶奇性概念と共役関係概念の連続性について。

# CVCM=等速円運動(Constant Velocity Circular Motion)
# Radian=角度(60分割)
CVCM<-function(Radian){
c0<-seq(0,2*pi,length=60)
# 大円
cx<-cos(c0)
cy<-sin(c0)
# 小円(奇数系)1個目
s1cx<-cos(c0)/2+cx[Radian]/2
s1cy<-sin(c0)/2+cy[Radian]/2
# 小円(奇数系)2個目
s2cx<-cos(c0)/2+cx[Radian]+cx[Radian]/2
s2cy<-sin(c0)/2+cy[Radian]+cy[Radian]/2
# 小円(偶数系)1個目
s1cx0<-cos(c0)/2
s1cy0<-sin(c0)/2
# 小円(偶数系)2個目
s2cx0<-cos(c0)/2-cx[Radian]
s2cy0<-sin(c0)/2-cy[Radian]
# 円描画
plot(cx,cy,asp=1,type="l",col=rgb(0,0,0),main="Even & Odd Circles",xlab="cos(θ)",ylab="sin(θ)")
# 塗りつぶし(円全体)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(奇数系小円1)
polygon(s1cx, #x
s1cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
# 塗りつぶし(奇数系小円2)
polygon(s2cx, #x
s2cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
# 塗りつぶし(偶数系小円1)
polygon(s1cx0, #x
s1cy0, #y
density=c(40), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
# 塗りつぶし(偶数系小円2)
polygon(s2cx0, #x
s2cy0, #y
density=c(40), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
text(0,0,"(0,0,0,…)",col=rgb(0,0,0))
text(cx[Radian],cy[Radian],"(1,1,1,…)",col=rgb(0,0,0))
text(cx[Radian]/2,cy[Radian]/2,"(1/2,1/2,1/2,…)",col=rgb(0,0,0))
# 対蹠の設定
segments(cx[Radian],cy[Radian],cx[Radian]/2,cy[Radian]/2,col=rgb(1,0,0))
segments(cx[Radian]/2,cy[Radian]/2,0,0,col=rgb(0,0,1))
# lines(s1cx,s1cy,col=rgb(0,1,0))
# lines(s1cx0,s1cy0,col=rgb(1,0,1))
# 凡例
legend("bottomright", legend=c("Even Circles","Odd Circles"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CVCM(i)
}
}, interval = 0.1, movie.name = "CVCM05.gif")
なお、この時点ではあくまで「原始座標群(Primitive Coordinate Group)=距離も方角も観測不可能な極座標系(Polar Coordinate System)」にユークリッド距離(Euclidean Distance)の概念が追加されただけで、まだデカルト座標系(Cartesian Coordinate System)の概念には到達していない事に気をつけなければなりません。
その一方でこの同心円比率何処かで見覚えが…そう、円に内接する正方形/立方体の「連続同心円構造」と一致するのですね。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

単位円筒(Unit Cylinder)との関係
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
【初心者向け】「単位円筒」から「単位球面」へ


連続同心円構造

| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 2^-1 | 2^-1(2^-0.5r) | 0.5 |
| 2 | 2^-1 | 2^-1d=2^-1*4 | 1 |
| 3 | 2^-1 | 2^-1a1=2^0a0 | sqrt(2)=1.414214 |
| 4 | 2^-1 | 2^-1a1(2^-0.5a0)*4 | 4sqrt(2)=5.656854 |
| 5 | 2^-0.5 | 2^-0.5(2^0r) | sqrt(2)/2=0.7071068 |
| 6 | 2^-0.5 | 2^-0.5d=2^-0.5*4 | sqrt(2)=1.414214 |
| 7 | 2^-0.5 | 2^-0.5a1=2^0a0 | 1 |
| 8 | 2^-0.5 | 2^-1a1(2^0.5a0)*4 | 4 |
| 9 | 2^0 | 2^0(2^-0.5R,2^0.5r) | 1 |
| 10 | 2^0 | 2^0d=2^0*4 | 2 |
| 11 | 2^0 | 2^0a1=2^0.5a0 | sqrt(8)=2sqrt(2)=2.828427 |
| 12 | 2^0 | 2^0a1(2^0.5a0)*4 | sqrt(32)=4sqrt(2)=5.656854 |
| 13 | 2^0.5 | 2^0.5(2^-0R,2^1r) | sqrt(2)=1.414214 |
| 14 | 2^0.5 | 2^0.5d=2^0.5*4 | 2sqrt(2)=2.828427 |
| 15 | 2^0.5 | 2^0.5a1=2^1a0 | 4 |
| 16 | 2^0.5 | 2^0.5a1(2^0a0)*4 | 8 |
| 17 | 2^1 | 2^1(2^1-0.5R,2^0.5r) | 2 |
そして上の「大円内を小円が回るアニメーション」を目にすれば、誰もが連想するのでは無いでしょうか。大円の半径(Major Radius)と小円の半径(Minor Radius)の組み合わせで規定されるトーラス(単数形torus/複数形tori)構造を…
【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ


実際、オイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)は、円に内接する正多角形の辺数が2辺(すなわち対蹠間を結ぶ一対の経路)から無限(すなわち無限円そのもの)に推移する過程で全体像が以下の様に推移する事を示唆しているのです。
【トーラス構造と古典数学】オイラーの多面体定理との統合?

①NoS(Number of Sides)=2,すなわち2辺形(Bilateral)…xyz座標{0,0,r}{0,0,-r}となる対蹠(Antipodes)間を結ぶ一対の半弧(各周長π*半径r)、あるいはその往復が軌跡として描く二重球面(各周長2πr)。球面sqrt(x^2+y^2+z^2)=半径rにおいて、対蹠間を結ぶ軸線に対して(互いに共役(Conjugate)関係にある座標の並びを結んだ)垂直方向の断面として現れる円弧sqrt(x^2+y^2)=半径rにとっては極限(X座標とY座標の消失点)であり、その平面上における観測は不可能。
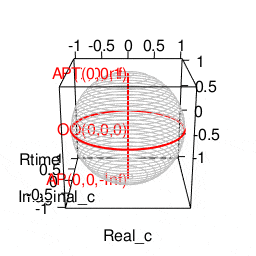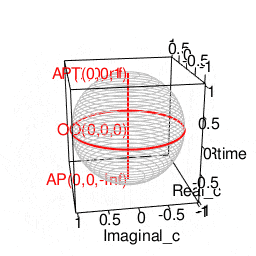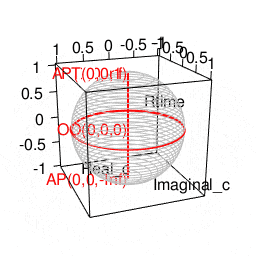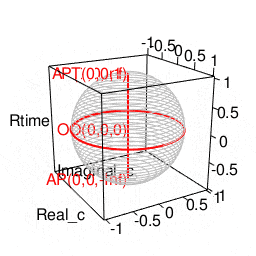
library(rgl)
# 円描写関数
f0<-function(x){exp(x*(0+1i))}
# 無限円(Infinity Circle)
radians0<-seq(0,60*pi,length=60)
Real0<-Re(f0(radians))
Imaginal0<-Im(f0(radians))
Rtime0<-numeric(60)
# 無限球面(Infinity Sphere)
radians<-seq(0,60*pi,length=3000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
# 工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
# > plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1
# 無限球面(Infinity Sphere)の描画
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),col=c(200,200,200))
# 無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(1,0,0),lwd=2)
# 観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(1,0,0),adj=1.0)
# 原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(1,0,0),adj=1.0)
# 原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text="AP(0,0,Inf)"
# 原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(1,0,0),adj=1.0)
# 対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text="AP(0,0,-Inf)"
# 対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)
# 立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere05")
# RD=2角形(Regular Digon)
# Radian=角度(60分割)
RD<-function(Radian){
c0<-seq(0,2*pi,length=60)
c1x<-cos(c0)
c1y<-sin(c0)
plot(c1x,c1y,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Henagon",xlab="cos(θ)",ylab="sin(θ)")
RD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),xlim=c(-1,1),ylim=c(-1,1),main="Regular Henagon",xlab="X",ylab="sqrt(1-X^2) & -sqrt(1-X^2)")
par(new=T)#上書き指定
plot(cx,-1*cy,asp=1,type="l",col=rgb(1,0,0),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
# 緯度(latitude)の描写
lat<-seq(-1,1,length=9)
for(i in lat){
segments(i,f0(i),i,-f0(i),col=c(200,200,200))
}
# 経度(Longitude)の描写
lon<-seq(-pi/2,pi/2,length=9)
for(i in lon){
par(new=T)#上書き指定
plot(cx,sin(i)*cy,asp=1,type="l",col=c(200,200,200),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
}
# 塗りつぶし
p_max<-15
p0<-seq(pi,0,length=p_max)
px_Hi<-rev(cos(p0))
px_Low<-rev(cos(p0*-1))
py_Hi<-rev(sin(p0))
py_Low<-rev(sin(p0*-1))
# 左側インジケータ描画(緑)
polygon(c(px_Hi[1:Radian],px_Low[Radian:1]), #x
c(py_Hi[1:Radian],py_Low[Radian:1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
# 右側インジケータ描画(赤)
polygon(c(px_Hi[p_max:Radian],px_Low[Radian:p_max]), #x
c(py_Hi[p_max:Radian],py_Low[Radian:p_max]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
}
# アニメーション
library("animation")
Time_Code=c(1:15,14:1)
saveGIF({
for (i in Time_Code){
RD(i)
}
}, interval = 0.1, movie.name = "RD01.gif")
全体としてはトーラス構造を保持しているが、以下の様に上掲の二重球面の半分しか使わない判断によってその特徴を放棄しているケースが多い。
-
経度(地球を横に輪切りにした断面円の角度)は±180度、緯度(地球を横に輪切りにした縦に輪切りにした断面円の角度)が±90度で表す。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
-
三次元極座標系(3Dimensional Polar Coordinate System)は水平角φを0~2πラジアン、垂直角θを半分の0~πラジアンの範囲で表す。
【初心者向け】「単位円筒」から「単位球面」へ
- 「互いに直角に交わる回転軸φ,θ,ψを操作する」オイラー角系(Eulerian Angle System)では発生する「ジンバル・ロック問題(Gimbal Lock Problem)」が、「直角に2回曲がる経路で対蹠と球面上の2点を結ぶ」四元数系(Quaternion System)では発生しない。オイラー角 - いろもの物理学者前野
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか?
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。
②NoS(Number of Sides)=3,すなわち正三角形(Equilateral Triangle)…球面sqrt(x^2+y^2+z^2)=半径rにおいて対蹠{0,0,-r}{0,0,r}間を結ぶ互いに共役(Conjugate)関係にある座標の並びを結んだ円弧sqrt(x^2+y^2)=半径rで観測され、平面充填性(Tesselation)と連続同心円構造を発揮する。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

単位円筒(Unit Cylinder)との関係
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
【初心者向け】「単位円筒」から「単位球面」へ


平面充当性(Tesselation)

連続同心円構造

| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 3^-1 | 3^-1(3^0r) | 1/2=0.5 |
| 2 | 3^-1 | 3^-1h=3^-1*3 | 3/2=1.5 |
| 3 | 3^-1 | 3^-1a1=3^0a0 | 2*sqrt(1.5)=2.44949 |
| 4 | 3^-1 | 3^-1a1(3^0a0)*3 | 6*sqrt(1.5)=7.348469 |
| 5 | 3^0 | 3^0(3^-1R,3^1r) | 1.0 |
| 6 | 3^0 | 3^0h=3^0*3 | 3.0 |
| 7 | 3^0 | 3^0a1=3^1a0 | 2*sqrt(3)=3.464102 |
| 8 | 3^0 | 3^0a1(3^1a0)*3 | 6*sqrt(3)=10.3923 |
| 9 | 3^1 | 3^1(3^0R) | 3.0 |
③NoS(Number of Sides)=4,すなわち正方形(Square)…球面sqrt(x^2+y^2+z^2)=半径rにおいて対蹠{0,0,-r}{0,0,r}間を結ぶ互いに共役(Conjugate)関係にある座標の並びを結んだ円弧sqrt(x^2+y^2)=半径rで観測され、同心円連続性と平面充填性(Tesselation)と立体充填性(Space Filling)に加え、ぞの四隅{0,0,0}{r,0,0}{0,r,0}{r,r,0}が既存の対蹠{0,0,r}{0,0,-r}と併せて三対の対蹠および正八面体を構成する。また同時に大半径r/2,小半径r/4のトーラス構造も観測される。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間
平面充当性(Tesselation)…さらにこの構造をそのまま立体化した立方体(Cube)も立体充填性(Space Filling)を備える。
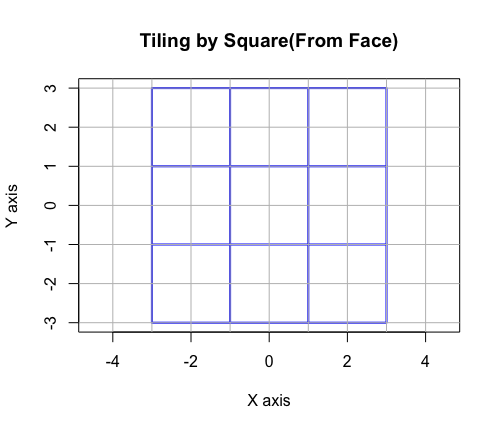
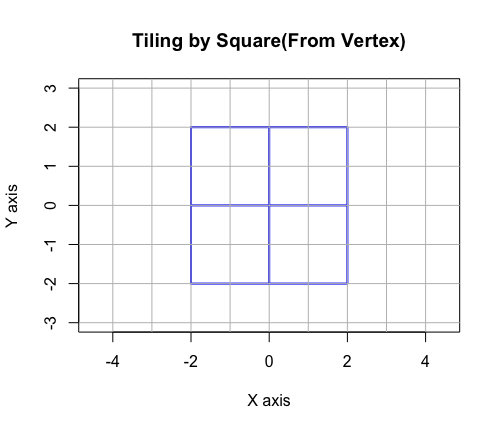
正八面体は三対の対蹠を備える。

④NoS(Number of Sides)=6以上…実は=NoS=3~6にかけて対蹠軸{-r,0,r}概念は正四面体(Regular Tetrahedron)、正六面体(Cube)、正八面体(Regular Octahedron)、正十二面体(Regular Dodecahedron)、正二十面体(Regular Icosahedron)といった正多面体が繰り広げる立体幾何学展開上の中核となる。
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…
正四面体(Regular Tetrahedron)…対蹠軸{-r,0,r}は1対。ただしこの図形のみ偶奇性の関係で2個セットで現れる。

正六面体(Cube)…対蹠軸{-r,0,r}は3対。
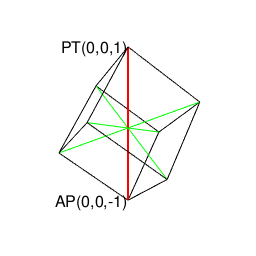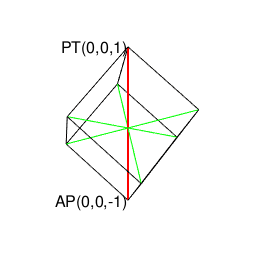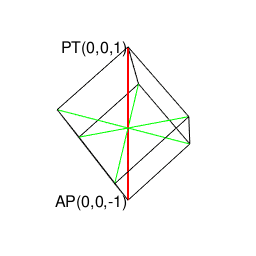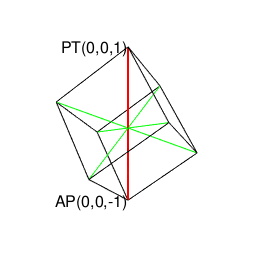
正八面体(Regular Octahedron)…対蹠軸{-r,0,r}は3対。
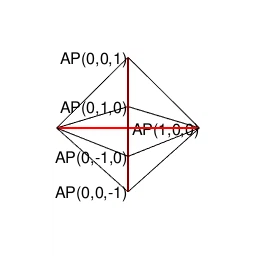
正十二面体(Regular Dodecahedron)…対蹠軸{-r,0,r}は10対。

正二十面体(Regular Icosahedron)…対蹠軸{-r,0,r}は6対。
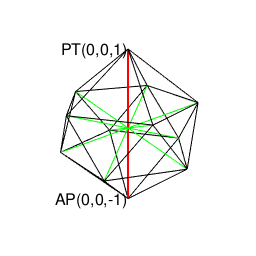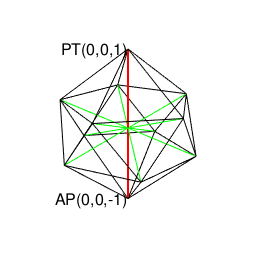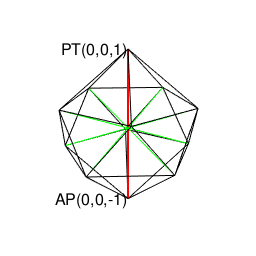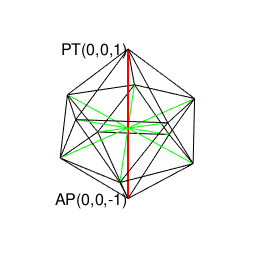
しかもこれらの図形の分類にはなんと素因数分解(Prime factorization)の概念導入が必要となった。そう、まさかの「またもやオイラー」φ関数の登場である。しかも、そこはかとなく漂う「群論の二項演算にまとめられそうな雰囲気」…・
【Rで九九】どうして36個の数字しか使われないのか?
-
2^n集(Set)…二辺形(Bilateral)と正方形(Squares)が分類される範疇。

-
3^n集(Set)…正四面体(Tetrahedrons)と正三角形(Triangles)が分類される範疇。

-
2^m*3^n集(Set)…正八面体(Octahedron)と正六面体(Cube)と正六角形(Hexagon)が分類される範疇。

-
2^n3^m5^l集(Set)…正十二面体(Dodecahedron)と正十二面体(Dodecahedron)が分類される範疇。

しかしそれも、球面sqrt(x^2+y^2+z^2)=半径rにおいて対蹠{0,0,-r}{0,0,r}間を結ぶ互いに共役(Conjugate)関係にある座標の並びを結んだ円弧sqrt(x^2+y^2)=半径rにおいて正六角形(Hexagon)が観測されると打ち止めとなる。そもそも結論から言えば正多角形/正多面体の世界において同心円連続性を備えるのは正三角形と正方形のみ、平面充填性(Tesselation)を備えるのは三角形と正方形と正六角形のみ、単独で立体充填性(Space Filling)を備えるのは立方体のみであった。

単位円筒(Unit Cylinder)との関係
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
【初心者向け】「単位円筒」から「単位球面」へ


(正三角形のそれを継承した)平面充当性(Tesselation)
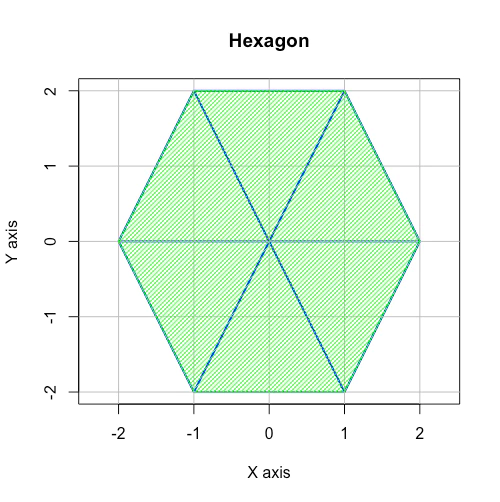
同心円連続性はもはや備わっていない。
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 6^-1 | 6^-1 | 1/6=0.1666666 |
| 2 | 6^-1 | 6^-1a1 | 1/6*1.154701=0.1924502 |
| 3 | 6^-1 | 6^-1a1*6 | 0.1924502*6=1.154701 |
| 4 | 6^-0.8394411 | 6^-0.8394411 | 0.1924502*1.154701=0.2222224 |
| 5 | ... | ... | ... |
| 6 | 6^-0.08027941 | 6^-0.08027921 | -0.8660254 |
| 7 | 6^0 | 6^0a0 | 1.0 |
| 8 | 6^0 | 6^0a0*6 | 6.0 |
| 9 | 6^0 | 6^0 | 1.0 |
| 10 | 6^0 | 6^0a1 | 1.333333 |
| 11 | 6^0 | 6^0a1*6 | 1.333333*6=7.999998 |
| 12 | 6^0.08027895 | 6^0.08027895 | 1.333333*0.8660254=1.333334 |
| 13 | ... | ... | ... |
| 14 | 6^0.7591625 | 6^0.7591625 | 4.500001*0.8660254=3.897115 |
| 15 | 6^1 | 6^1a0 | 6/1.333333=4.500001 |
| 16 | 6^1 | 6^1a0*6 | 4.500001*6=27.00001 |
| 17 | 6^1 | 6^1 | 6.0 |

以降も有効な数理(Mathematical Things)はオイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)のみとなります。正多角形(Regular Polygon)の辺数が無限円(Unlimited Circle)のそれ(すなわち辺数Inf,辺長1/Inf=0)に到達するまで、そのトーラス構造上の小半径が無限小(-Inf)へと収束を続けるだけなのです。そこはかとなく、あらゆる生物が滅び尽くした「死の惑星(Planet of the Dead)」が、静かに悠久の時を経ておもむろにそれ自体の死に向かう終末的光景が脳裏に浮かんでしまいます。さて、このイメージ正解か否や?
【トーラス構造と古典数学】何故「正方形」ではCos(θ)+Sin(θ)iが成立するのか?

素数2,3,5なる概念導入こそが数理の始まり?
そろそろ次の投稿に向けてのまとめに移ります。この投稿では無限直線(Infinity Line)/無限円(Infinity Circle)/無限球面(Infinity Sphere)の世界観において、以下が成立するのを確かめました。
-
群(Group)としての成立条件「単位元と逆元の存在と結合法則の成立」を満たす事が、直径(Diameter){-r,0,r}の概念追加と密接な関係にある事。
【Rで球面幾何学】単位円と単位球 - おそらくその事は、この方面における正多面体幾何学(Regular Polyhedron Geometry)の展開が「2^n集(Set),3^n集(Set),2^m*3^n集(Set),2^n3^m5^l集(Set)」なる素因数分解(Prime Factorization)概念の導入、とりわけ2^n集(Set)概念の導入と密接な関係にありそうな事。
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…
なんと「オイラーの公式(Eulerian Formula)Cos(θ)+Sin(θ)iおよびその一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)」概念と「オイラーの多面体定理(Eulerian Polyhedron Theorem)V(ertexes=頂点数)-E(dges=辺数)+F(aces=面数)=2(対蹠数)」概念の連動に続いて「オイラーのφ関数(Eulerian Totient Function)」概念が統合され様としている?
【Rで九九】どうして36個の数字しか使われないのか?
そんな感じで以下続報…


