【数学溢れ話】【Token】どうして36個の数字しか使われないのか？ #R

数理モデル(Mathematical model)の世界では、しばしば単純な問いに応える為に複雑な演算を重ねる必要が生じます。
【初心者向け】Rからxtableを用いて掛け算九九表のHTMLを出力する。

	1x	2x	3x	4x	5x	6x	7x	8x	9x
1y	1	2	3	4	5	6	7	8	9
2y	2	4	6	8	10	12	14	16	18
3y	3	6	9	12	15	18	21	24	27
4y	4	8	12	16	20	24	28	32	36
5y	5	10	15	20	25	30	35	40	45
6y	6	12	18	24	30	36	42	48	54
7y	7	14	21	28	35	42	49	56	63
8y	8	16	24	32	40	48	56	64	72
9y	9	18	27	36	45	54	63	72	81

有名な例の一つが「どうして掛け算の九九には36個の数字しか登場しないのか」なる小学生でも邂逅する疑問で、その答えを得るには素因数分解 (Prime Factorization)の世界に足を踏み入れないといけません。
まさかのNP困難？「九九って36種類しか数がないの不思議だよな」から始まる数学談義

#エラトステネスの篩（ふるい,Sieve of Eratosthenes）による合成数（Composite Number）の振るい落とし。

まずは基本中の基本。「素数（Prime Number）とは何か」について以下の定義を借用します。
The Murderous Maths Sieve of Eratosthenes

吉田武「オイラーの贈物」「基礎理論(Basic Theory)」「素数（Prime Number）と合成数（Composite Number）」より

自然数において1とその数自身(The Number Itself)の他に約数（Divisor）を持たない数を素数（Prime Number）という。そしてそれ以外の、すなわちいずれかの素数の積、すなわち倍数（Multiple）として表現可能な、すなわち素因数分解（Prime Factorization）可能な数を合成数（Composite Number）という。
自然数2は唯一の偶数の素数であり、偶素数（Even Prime Number）とも呼ばれる。
素因数分解は掛ける順番を考慮しないでよければ一意に定まる。これを素因数分解の一意性（Uniqueness）という。
具体的な素数の求め方としてはエラトステネスの篩（ふるい,Sieve of Eratosthenes）が素数を組織的に求める方法として現在なおも意味を保ち続けている。

エラトステネスの篩（ふるい,Sieve of Eratosthenes）

まずは最小の素数2で割り切れる数、すなわち2の倍数（Multiple）あるいは偶数（Even Numbers）を除去する。かくして1を除く奇数(Odd Numbers)だけが残る。
残った数の先頭である3の倍数6,9,12…を除去する。
これをガウスの記号（Gaus's symbol）すなわちNを超えない最大の整数[N]の平方根、すなわち[sqrt(N)]まで繰り返す。

#上掲の定義に従って１を除いた奇数の自然数（上限100）から検討を開始する。
Evaluation_Target<-c(3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45, 47,49,51,53,55,57,59,61,63,65,67,69,71,73,75,77,79,81,83,85,87,89,91,93,95,97,99)
#この単元は100を最大数とするので[sqrt(100)]すなわち検討対象が10を超えたら検討を終了する。
Evaluation_Max<-c(10)
#開始時点で素数リストは2のみ
Prime_Number_List<-c(2)
#具体的検討過程①検討対象の先頭の数字を取り出す。まずは３が出てくる。
Current_Prime_Number<-Evaluation_Target[1]
Current_Prime_Number
[1] 3
#②取り出した数字が検討の上限を超えてたら検討終了。そうでなければ、取り出した数字を素数リストに追加してその倍数を検討対象リストから除去する。まずは上限以下のケースから開始。
Current_Prime_Number_List <-c(Prime_Number_List,Current_Prime_Number)
Current_Prime_Number_List
[1] 2 3
Natural_Number_Coefficient<-c(1:100)
Current_Multiple_Sequence<-Natural_Number_Coefficient*Current_Prime_Number
Current_Multiple_Sequence
[1] 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66
[23] 69 72 75 78 81 84 87 90 93 96 99 102 105 108 111 114 117 120 123 126 129 132
[45] 135 138 141 144 147 150 153 156 159 162 165 168 171 174 177 180 183 186 189 192 195 198
[67] 201 204 207 210 213 216 219 222 225 228 231 234 237 240 243 246 249 252 255 258 261 264
[89] 267 270 273 276 279 282 285 288 291 294 297 300
Current_Evaluation_list <- setdiff(Evaluation_Target, Current_Multiple_Sequence)
Current_Evaluation_list
[1] 5 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 83 85 89 91
[31] 95 97

#③次の検討対象の先頭の数字を取り出す。５が出てくる。
Current_Prime_Number<-Current_Evaluation_list[1]
Current_Prime_Number
[1] 5
#④繰り返す。
Current_Prime_Number_List <-c(Prime_Number_List,Current_Prime_Number)
Current_Prime_Number_List
[1] 2 3 5
Current_Multiple_Sequence<-Natural_Number_Coefficient*Current_Prime_Number
Current_Evaluation_list <- setdiff(Current_Evaluation_list, Current_Multiple_Sequence)
Current_Evaluation_list
[1] 7 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 83 89 91 97
#⑤次の検討対象の先頭の数字を取り出す。７が出てくるので繰り返す。
Current_Prime_Number<-Current_Evaluation_list[1]
Current_Prime_Number
[1] 7
Current_Prime_Number_List <-c(Prime_Number_List,Current_Prime_Number)
Current_Prime_Number_List
[1] 2 3 5 7
Current_Multiple_Sequence<-Natural_Number_Coefficient*Current_Prime_Number
Current_Evaluation_list <- setdiff(Current_Evaluation_list, Current_Multiple_Sequence)
Current_Evaluation_list
[1] 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
#⑥次の検討対象の先頭の数字を取り出す。11が出てくる。検討の上限を超えたので検討中の素数リストに残りを加えて処理終了。

Prime_Number_List<-c(Current_Prime_Number_List,Current_Evaluation_list)
Prime_Number_List
[1] 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

上掲プロセスの関数化

Prime_Number_Choosing<-function(Calculation_Max){
#「検討の上限」を準備する。
Evaluation_Max<-sqrt(Calculation_Max)

#「１を除く奇数の数列」を準備する。
Allmost_Natural_number_list<-c(1:Calculation_Max) #1を除く
Odd_General_Term<-function(x){2*x+1}
Allmost_Odd_Sequence<-Odd_General_Term(Allmost_Natural_number_list)
Evaluation_Target<-Allmost_Odd_Sequence[Allmost_Odd_Sequence <= Calculation_max]

#「最初の素数2のみが入った検討済み素数の数列」を準備する。
Prime_Number_List <-c("2")
#上掲処理を整理した抽出過程。
while(Evaluation_Target[1] <= Evaluation_Max){
Prime_Number_List <-c(Prime_Number_List,Evaluation_Target[1])
Current_Multiple_Sequence<-Allmost_Natural_number_list*Evaluation_Target[1]
Evaluation_Target <- setdiff(Evaluation_Target, Current_Multiple_Sequence)
}
Prime_Number_List<-c(Prime_Number_List,Evaluation_Target)
return(c(Prime_Number_List))
}
Prime_Number_Choosing(100)#25個
[1] "2" "3" "5" "7" "11" "13" "17" "19" "23" "29" "31" "37" "41" "43" "47" "53" "59" "61"
[19] "67" "71" "73" "79" "83" "89" "97"
#次の素数101はCalculation_Maxを10201以上に上げないと登場しない。しかも何故か計算エラーが…
Prime_Number_Choosing(10300)
while (Evaluation_Target[1] <= Evaluation_Max) { でエラー:
TRUE/FALSE が必要なところが欠損値です

#オイラーのφ関数(Euler's Totient Function)

実際の素数の求め方はこんな感じですが「ある数までに含まれる互いに素な数字の数」なら別の計算でもっと簡単に求められます。それがオイラーのφ関数(Euler's Totient Function)なんですね。
オイラーのφ関数 - Wikipedia

Python で素因数分解 ---　R の勝ちかな？

install.packages("gmp")
install.packages("gmp")Installing package into ‘C:/Users/81806/Documents/R/win-library/3.5’(as ‘lib’ is unspecified)trying URL 'https://cran.rstudio.com/bin/windows/contrib/3.5/gmp_0.5-13.5.zip'Content type 'application/zip' length 1110866 bytes (1.1 MB)downloaded 1.1 MB
package ‘gmp’ successfully unpacked and MD5 sums checked
The downloaded binary packages are in C:\Users\81806\AppData\Local\Temp\RtmpyQC7uP\downloaded_packages> library(gmp)
 次のパッケージを付け加えます: ‘gmp’ 
 以下のオブジェクトは ‘package:base’ からマスクされています: 
     %*%, apply, crossprod, matrix, tcrossprod 
Warning message: パッケージ ‘gmp’ はバージョン 3.5.3 の R の下で造られました
factorize(120)
Big Integer ('bigz') object of length 5:
[1] 2 2 2 3 5

実際のgmpライブラリ動作例

factorize(12)
Big Integer ('bigz') object of length 3:
[1] 2 2 3
12*(1-1/2)*(1-1/3)
[1] 4
#実際に全列挙すれば，1,5,7,11 の 4個

factorize(90)
Big Integer ('bigz') object of length 4:
[1] 2 3 3 5
90*(1-1/2)*(1-1/3)*(1-1/5)
[1] 24

#実際に全列挙すれば，2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89の24個

それでは1桁の自然数同士の掛け合わせが2桁以内に収まってるケース、すなわち掛け算の九九で使われている数字について当て嵌めていきましょう。

###2^n集(Set)
2,4,8,16,32,64の6個

factorize(2)
Big Integer ('bigz') :
[1] 2

2*(1-1/2)
[1] 2
factorize(4)
Big Integer ('bigz') object of length 2:
[1] 2 2
4*(1-1/2)
[1] 2

factorize(8)
Big Integer ('bigz') object of length 3:
[1] 2 2 2

8*(1-1/2)
[1] 4

factorize(16)
Big Integer ('bigz') object of length 4:
[1] 2 2 2 2
16*(1-1/2)
[1] 8

factorize(32)
Big Integer ('bigz') object of length 5:
[1] 2 2 2 2 2
32*(1-1/2)
[1] 16

factorize(64)
Big Integer ('bigz') object of length 6:
[1] 2 2 2 2 2 2
64*(1-1/2)
[1] 32

###3^n集(set)
3,9,27,81の4個

factorize(3)
Big Integer ('bigz') :
[1] 3
3*(1-1/3)
[1] 2

factorize(9)
Big Integer ('bigz') object of length 2:
[1] 3 3

9*(1-1/3)
[1] 6

factorize(27)
Big Integer ('bigz') object of length 3:
[1] 3 3 3
27*(1-1/3)
[1] 18

factorize(81)
Big Integer ('bigz') object of length 4:
[1] 3 3 3 3
81*(1-1/3)
[1] 54

###5^n集(Set)
5,25の2個

factorize(5)
Big Integer ('bigz') :
[1] 5
5*(1-1/5)
[1] 4

factorize(25)
Big Integer ('bigz') object of length 2:
[1] 5 5
25*(1-1/5)
[1] 20

###2^m3^n集(Set)
6,12,18,24,36,48,54,72,96の9個だが96がレンジ外（222223が1桁の計算に収まらない）。

factorize(6)
Big Integer ('bigz') object of length 2:
[1] 2 3
6*(1-1/2)*(1-1/3)
[1] 2

factorize(12)
Big Integer ('bigz') object of length 3:
[1] 2 2 3
12*(1-1/2)*(1-1/3)
[1] 4

factorize(18)
Big Integer ('bigz') object of length 3:
[1] 2 3 3
18*(1-1/2)*(1-1/3)
[1] 6

factorize(24)
Big Integer ('bigz') object of length 4:
[1] 2 2 2 3
24*(1-1/2)*(1-1/3)
[1] 8

factorize(36)
Big Integer ('bigz') object of length 4:
[1] 2 2 3 3
36*(1-1/2)*(1-1/3)
[1] 12

factorize(48)
Big Integer ('bigz') object of length 5:
[1] 2 2 2 2 3
48*(1-1/2)*(1-1/3)
[1] 16

factorize(54)
Big Integer ('bigz') object of length 4:
[1] 2 3 3 3
54*(1-1/2)*(1-1/3)
[1] 18

factorize(72)
Big Integer ('bigz') object of length 5:
[1] 2 2 2 3 3
72*(1-1/2)*(1-1/3)
[1] 24

factorize(96)
Big Integer ('bigz') object of length 6:
[1] 2 2 2 2 2 3
96*(1-1/2)*(1-1/3)
[1] 32

###7^n集(Set)
7,49の2個

factorize(7)
Big Integer ('bigz') :
[1] 7
7*(1-1/7)
[1] 6

factorize(49)
Big Integer ('bigz') object of length 2:
[1] 7 7
49*(1-1/7)
[1] 42

###2^m5^n集(Set)
10,20,40,50,80の5個だが20,80がレンジ外（225と2222*5が1桁の計算に収まらない）

factorize(10)
Big Integer ('bigz') object of length 2:
[1] 2 5
10*(1-1/2)*(1-1/5)
[1] 4

factorize(20)
Big Integer ('bigz') object of length 3:
[1] 2 2 5
20*(1-1/2)*(1-1/5)
[1] 8

factorize(40)
Big Integer ('bigz') object of length 4:
[1] 2 2 2 5
40*(1-1/2)*(1-1/5)
[1] 16

factorize(50)
Big Integer ('bigz') object of length 3:
[1] 2 5 5
50*(1-1/2)*(1-1/5)
[1] 20

factorize(80)
Big Integer ('bigz') object of length 5:
[1] 2 2 2 2 5
80*(1-1/2)*(1-1/5)
[1] 32

###2^m7^n集(Set)
14,28,56,98の4個だが98がレンジ外（2222*7が1桁の計算に収まらない）

factorize(14)
Big Integer ('bigz') object of length 2:
[1] 2 7
14*(1-1/2)*(1-1/7)
[1] 6

factorize(28)
Big Integer ('bigz') object of length 3:
[1] 2 2 7
28*(1-1/2)*(1-1/7)
[1] 12

factorize(56)
Big Integer ('bigz') object of length 4:
[1] 2 2 2 7
56*(1-1/2)*(1-1/7)
[1] 24

factorize(98)
Big Integer ('bigz') object of length 3:
[1] 2 7 7
98*(1-1/2)*(1-1/7)
[1] 42

###3^m*5^n集(Set)

15,45,75の3個だが75がレンジ外（355が1桁の計算に収まらない）

factorize(15)
Big Integer ('bigz') object of length 2:
[1] 3 5
15*(1-1/3)*(1-1/5)
[1] 8

factorize(45)
Big Integer ('bigz') object of length 3:
[1] 3 3 5
45*(1-1/3)*(1-1/5)
[1] 24

factorize(75)
Big Integer ('bigz') object of length 3:
[1] 3 5 5
75*(1-1/3)*(1-1/5)
[1] 40

###3^m*7^n集(Set)
21,63の2個。

factorize(21)
Big Integer ('bigz') object of length 2:
[1] 3 7
21*(1-1/3)*(1-1/7)
[1] 12

factorize(63)
Big Integer ('bigz') object of length 3:
[1] 3 3 7
63*(1-1/3)*(1-1/7)
[1] 36

###2^l3^m^5^n集(Set)
30,60,90の3個だが60,90がレンジ外（2235と233*5が1桁の計算に収まらない）

factorize(30)
Big Integer ('bigz') object of length 3:
[1] 2 3 5
30*(1-1/2)*(1-1/3)*(1-1/5)
[1] 8

factorize(60)
Big Integer ('bigz') object of length 4:
[1] 2 2 3 5
60*(1-1/2)*(1-1/3)*(1-1/5)
[1] 16
factorize(90)
Big Integer ('bigz') object of length 4:
[1] 2 3 3 5
90*(1-1/2)*(1-1/3)*(1-1/5)
[1] 24

###5^m*7^n集(Set)
35の1個

factorize(35)
Big Integer ('bigz') object of length 2:
[1] 5 7
35*(1-1/5)*(1-1/7)
[1] 24

###2^l3^m^7^n集(Set)
42,84の2個だが84がレンジ外（2237が1桁の計算に収まらない）

factorize(42)
Big Integer ('bigz') object of length 3:
[1] 2 3 7
42*(1-1/2)*(1-1/3)*(1-1/7)
[1] 12

factorize(84)
Big Integer ('bigz') object of length 4:
[1] 2 2 3 7
84*(1-1/2)*(1-1/3)*(1-1/7)
[1] 24

###2^l5^m^7^n集(Set)
70の1個だがレンジ外（25*7が1桁の計算に収まらない）

factorize(70)
Big Integer ('bigz') object of length 3:
[1] 2 5 7
70*(1-1/2)*(1-1/5)*(1-1/7)
[1] 24

###2^h3^l5^m^7^n集(Set)
10以下の素数をすべて含んだ形だが、どうやってもレンジ外となる。

factorize(210)
Big Integer ('bigz') object of length 4:
[1] 2 3 5 7
210*(1-1/2)*(1-1/3)*(1-1/5)*(1-1/7)
[1] 48

まとめると…

1が1個
2^n集(Set)(2,4,8,16,32,64)が6個
3^n集(Set)(3,9,27,81)が4個
5^n集(Set)(5,25)が2個
2^m*3^n集(Set)(6,12,18,24,36,48,54,72,96)が9個だが96がレンジ外（22222*3が1桁の計算に収まらない）
7^n集(Set)(7,49)が2個

ここまでで掛ける側に登場する数字(1~9)は網羅。小計23個。

2^m*5^m集(Set)(10,20,40,50,80)が5個だが20,80がレンジ外（225と22**22*5が1桁の計算に収まらない）
2^m*7^m集(Set)(14,28,56,98)が4個だが98がレンジ外（22227が1桁の計算に収まらない）
3^m*5^n集(Set)(15,45,75)が3個だが75がレンジ外（355が1桁の計算に収まらない)
3^m*7^n集(Set)(21,63)が2個
2^l*3^m^5^n集(Set)(30,60,90)が3個だが60,90がレンジ外（2235と2335が1桁の計算に収まらない）
5^m*7^n集(Set)(35)が1個
2^l*3^m^7^n集(Set)(42,84)が2個だが84がレンジ外（223*7が1桁の計算に収まらない）
2^l*5^m^7^n集(Set)(70)が1個だがレンジ外（257が1桁の計算に収まらない）

追加で13個。かくして九九に使用される数字は36個となる。除外されたのは…

100以下1桁以上の素数が

11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97の21個

その倍数まで含めると

11集(Set)(11,22,33,44,55,66,77,88,99)の9個
13集(Set)(13,26,39,52,65,78,91)の7個
17集(Set)(17,34,51,68,85)の5個
19集(Set)(19,38,57,76,95)の5個
23集(Set)(23,46,69,92)の4個
29集(Set)(29,58,87)の3個
31集(Set)(31,62,93)の3個
37集(Set)(37,74)の2個
41集(Set)(41,82)の2個
43集(Set)(43,86)の2個
47集(Set)(47,94)の2個
単独出現(53,59,61,67,71,73,79,83,89,97)が10個

ここまでの合計が54個。そして合成数だが1桁の計算に収まらないのが20,60,70,75,80,84,90,96,98の9個

#九九で使われる数(36個)
c009<-c(c(1),c(2,4,8,16,32,64),c(3,9,27,81),c(5,25),c(6,12,18,24,36,48,54,72),c(7,49))
c100<-c(c(10,40,50),c(14,28,56),c(15,45),c(21,63),c(30),c(35),c(42))
c99<-c(c009,c100)
length(c99)
[1] 36

#レンジ超過除外分(9個)
ce99<-c(20,60,70,75,80,84,90,96,98)

#100以下1桁以上の素数とその倍数(54個)

d100<-c(c(11,22,33,44,55,66,77,88,99),c(13,26,39,52,65,78,91),c(17,34,51,68,85),c(19,38,57,76,95),c(23,46,69,92),c(29,58,87),c(31,62,93),c(37,74),c(41,82),c(43,86),c(47,94),c(53,59,61,67,71,73,79,83,89,97))

length(d100)

[1] 54

ttl01<-c(c99,ce99,d100)
setdiff(c(1:99),ttl01)

integer(0)

「レンジオーバー項目の発見と除去」は結局、最終的に人力で遂行。何かうまいアルゴリズムがありますかね？
ナップサック問題-Wikipedia-

#「重複組み合わせ（記号Ｈ）」による算出方法？
ちなみに一般には「九九で覚えるべき計算が36種類」である事と混同されてる側面も?
かけ算九九は36パターンだけでOK

では、いくつ覚えればいいかというと、「１」を含むかけ算（１の段）は計算しなくても分かるので外すとして、「２」から「９」までの８種類の数を、２つ取り出す場合の組み合わせの数だけとなります。その際、３×３のように同じ数を取り出す組み合わせも１つとしてカウントします。これは数学でいう「重複組み合わせ（記号Ｈ）」で求められ、全部で36個の組み合わせということになりますが、表を作って確かめた方が分かりやすいです。

【初心者向け】階乗と順列と組み合わせ

#「重複を含まない」1から9の数字の組み合わせも9C2は36個。
> choose(9,2)
[1] 36
> combn(c(1:9), 2)
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17]
[1,]    1    1    1    1    1    1    1    1    2     2     2     2     2     2     2     3     3
[2,]    2    3    4    5    6    7    8    9    3     4     5     6     7     8     9     4     5
     [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32] [,33]
[1,]     3     3     3     3     4     4     4     4     4     5     5     5     5     6     6     6
[2,]     6     7     8     9     5     6     7     8     9     6     7     8     9     7     8     9
     [,34] [,35] [,36]
[1,]     7     7     8
[2,]     8     9     9

#これから自明の場合(Trivial Case)で覚える必要がない「1の段(1*1~1*9)」を除き、かつ同数同士の組み合わせ「1*1=1,2*2=4,…,9*9=81」を足した重複組み合わせ8H2=(8-2-1)H2=9H2も結果は36個となる。
> factorial(9)/factorial(2)/factorial(9-2)
[1] 36

九九の答えが36種類であることの証明

規則性が見えそうで見えない・・・

色々擦り合わせが必要なのは明瞭ですが、とりあえず以下続報…

#ここまでのまとめ（全体像の俯瞰）。
たかが九九、されど九九…整数論(Number Theory)の一環に足を踏み入れた途端、急激に難易度が上がります。
数論 -Wikipedia-

数、特に整数およびそれから派生する数の体系（代数体、局所体など）の性質について研究する数学の一分野である。整数論とも言う。
ガウスは「数学は科学の王女であり、数論は数学の王女である」という言葉を残した。
永らく実用性は無いと言われてきたが、近年暗号（RSA,楕円曲線暗号）や符号により計算機上での応用が発達しつつある。

最初に投稿した時点では「族」という言葉を使ったが、「族（Family）」なる用語には数学的にまた別の意味が与えられているので「集（Set）」なるより一般的数学用語に差し替えた。まぁ集合の一種には違いないので…

族 (数学) - Wikipedia

添字付けされた元（要素）の（一般には非可算無限個の）集まりで、対、n-組、列などの概念の一般化である。系（けい、collection）と呼ぶこともある。元がどのような対象であるかによって、点族、集合族（集合系）、関数族（関数系）などと呼ばれる。

一方、ここに登場した「レンジオーバー問題」は、どうやらNP(Non-deterministic Polynomial time（非決定性多項式時間）の略。複雑性クラスのひとつ)困難(NP-hard)問題の一環としての「ナップサック問題（Knapsack problem）」に分類される模様だが、あまり詳しくないので現時点では放置。

NP困難 -Wikipedia-

計算量理論において、問題が「NPに属する任意の問題と比べて、少なくとも同等以上に難しい」ことである。正確にいうと問題HがNP困難であるとは、「NPに属する任意の問題LがHへ帰着可能である」と定義される。

ナップサック問題 -Wikipedia-

計算複雑性理論における計算の難しさの議論の対象となる問題の一つで、「容量Cのナップサックが一つと、n種類の品物（各々、価値pi,容積ci）が与えられたとき、ナップサックの容量Cを超えない範囲でいくつかの品物をナップサックに詰め、ナップサックに入れた品物の価値の和を最大化するにはどの品物を選べばよいか」という整数計画問題である。

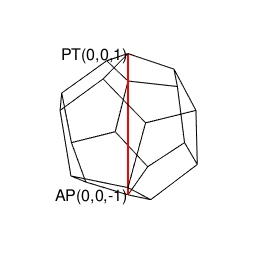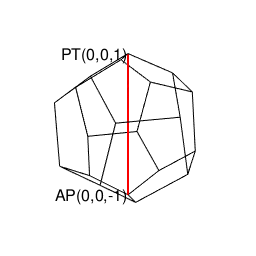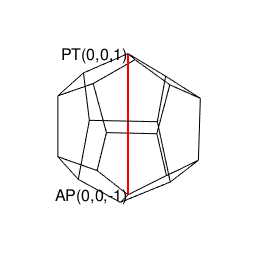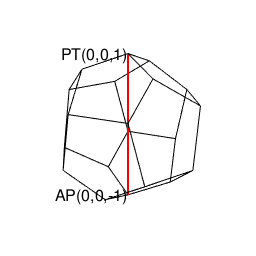
ところで、ここでこれまで傾注してきた幾何学世界(Geometry Set)からのアプローチに視野を転じますと、また別の景色が浮かび上がってくるのです。

「(辺長無限小1/Infの無限数Infの辺=頂点の集合と見做せる)円そのもの(Circle Itself)/球面そのもの(Sphere Itself)」を出発点とする。
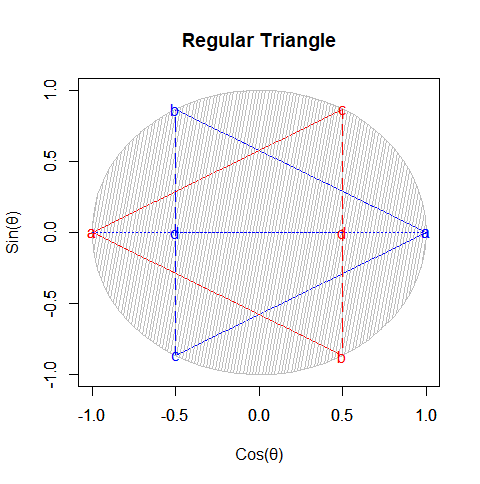
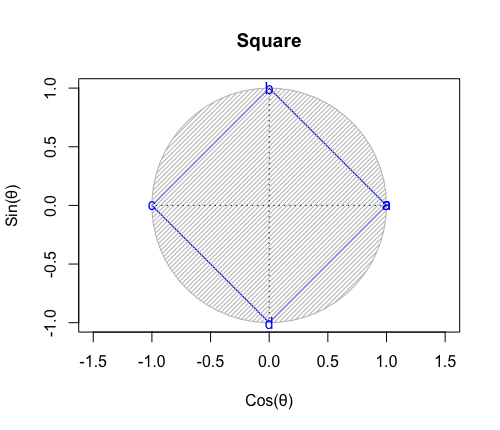
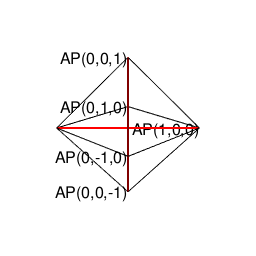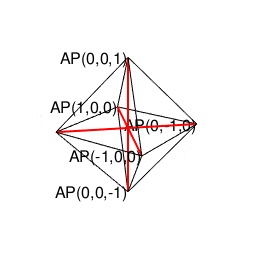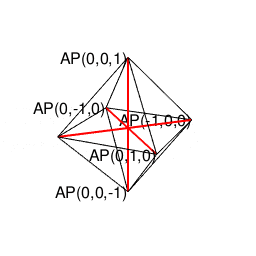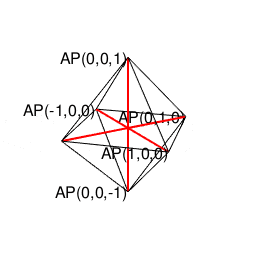
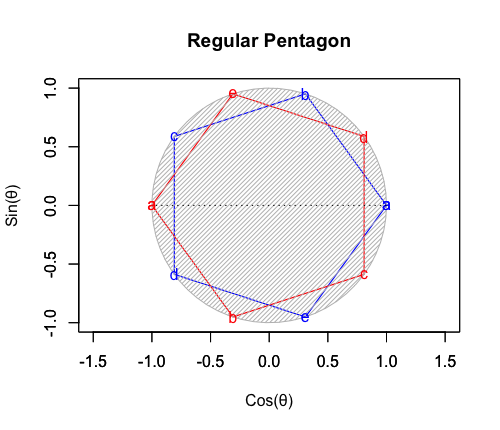
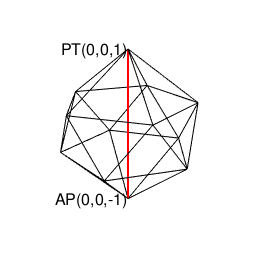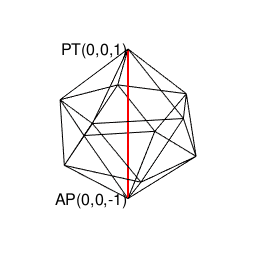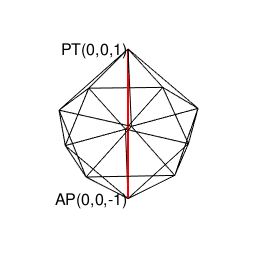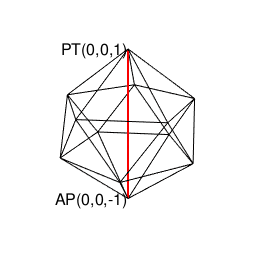
「正多面体世界(Regular Polyhedron Set)」においては「2^n集」「3^n集」「2^n3^m集」といった概念(Concept)の組み合わせだけで構築可能な世界(正四面体、正六面体、正八面体に加え「断面」として三角形、四角形、正六角形が登場)と「5^n集」概念も導入(Introduction)された世界(正十二面体、正二十面体)の間に明らかに扱い上の難易度レベルの差が存在する。
ましてや「7^n集」概念まで導入された世界なんて…到底想像力がついていかない。

【Rで球面幾何学】平方眼と立方眼の小宇宙(Square & Cube Grid Set)について。

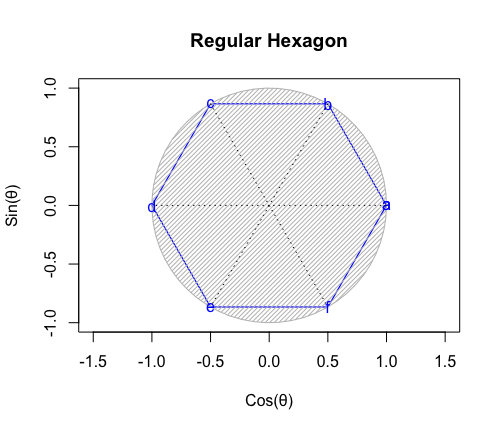
その一方で正六面体はその存在自体が既に「5^n集」の世界に足を踏み入れているという話も…で、ここに「（閉じた系(Close System)を構築すべく、その系で扱いきれない数理をまとめてある種の「誤差」として切り捨てる）隔壁(Partition)問題」が急浮上してくる訳である。

【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。

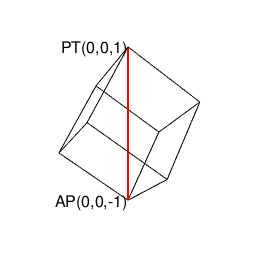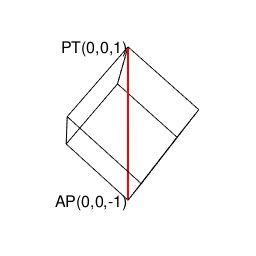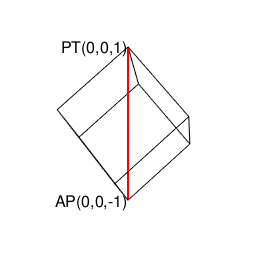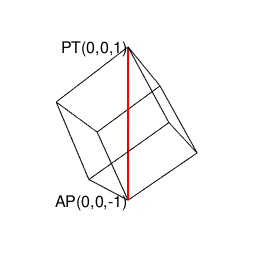
そう、まさにユークリッド幾何学と非ユークリッド幾何学、ニュートン力学と量子力学の狭間に登場してくるアレ…現代人は何でもここからの逆算で考えねばならなくなってしまったのです。
【Rで射影幾何学】そもそも「幾何学」とは何か？

一方「九九世界(Times Tables Set)」は平然と「5^n集」の概念ばかりか「7^n集」の概念まで平然と足を踏み入れてきます。ちなみに海外ではTimes Tablesというと12*12で覚えさせられる模様…それちょっと欲張り過ぎじゃないですかね？　そもそも閉じた系(Closed System)感が希薄だし、実際脱落者もゴロゴロ出すとか…
かけ算九九、オーストラリアではどう学ぶ？

いずれにせよ私の関心は「人類はその認識可能範囲外を跋扈する絶対他者に対し、如何なる段階的隔壁を構築してきたか」にあり、それがこうやって「２集・3集まで含む範囲内」「５集まで含む範囲内」「7集以上も視野に入れた範囲内」みたいな形で具体的数理(Mathematical things)上の定義(Definition)に統合されていくプロセス自体が楽しかったりします。やはり根はあくまで文系人間(Humanities Bacground Set)の一員なんですね…
【数理Computingの基礎】（人類の限界を乗り越えんとする）N進法/p進数の世界？

ならば、この態度に対峙すべき理系人間(Technical Bacground Set)の矜恃とは？　
「矜持」の正しい使い方と「矜恃」との違いについて
これについても様々な答えが考えられそうですが（その同様の形での数理的裏付けも含め）以下続報…

	1x	2x	3x	4x	5x	6x	7x	8x	9x
1y	1	2	3	4	5	6	7	8	9
2y	2	4	6	8	10	12	14	16	18
3y	3	6	9	12	15	18	21	24	27
4y	4	8	12	16	20	24	28	32	36
5y	5	10	15	20	25	30	35	40	45
6y	6	12	18	24	30	36	42	48	54
7y	7	14	21	28	35	42	49	56	63
8y	8	16	24	32	40	48	56	64	72
9y	9	18	27	36	45	54	63	72	81

	1x	2x	3x	4x	5x	6x	7x	8x	9x
1y	1	2	3	4	5	6	7	8	9
2y	2	4	6	8	10	12	14	16	18
3y	3	6	9	12	15	18	21	24	27
4y	4	8	12	16	20	24	28	32	36
5y	5	10	15	20	25	30	35	40	45
6y	6	12	18	24	30	36	42	48	54
7y	7	14	21	28	35	42	49	56	63
8y	8	16	24	32	40	48	56	64	72
9y	9	18	27	36	45	54	63	72	81

	1x	2x	3x	4x	5x	6x	7x	8x	9x
1y	1	2	3	4	5	6	7	8	9
2y	2	4	6	8	10	12	14	16	18
3y	3	6	9	12	15	18	21	24	27
4y	4	8	12	16	20	24	28	32	36
5y	5	10	15	20	25	30	35	40	45
6y	6	12	18	24	30	36	42	48	54
7y	7	14	21	28	35	42	49	56	63
8y	8	16	24	32	40	48	56	64	72
9y	9	18	27	36	45	54	63	72	81