【トーラス構造と古典数学】オイラーの多面体定理との統合？

単位円筒(Unit Cylinder)／単位球面(Unit Sphere)の概念(Concept)がトーラス(単数形torus,複数形tori)構造と可換である事自体は既に以前の投稿で指摘しています。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。

XY軸（円弧）

ZX軸（Cos波）

ZY軸（Sin波）

【初心者向け】「単位円筒」から「単位球面」へ


【Rで球面幾何学】「単位円筒」から「トーラス構造」へ

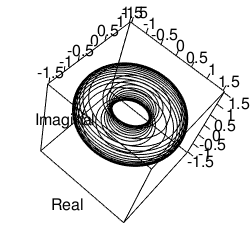
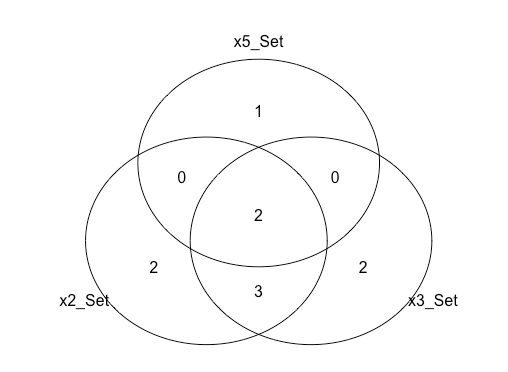
ちなみに「オイラーの多面体定理」では2,「オイラーの多角形定理」では意味論的統制(Semantic Control)によって0~2の間を変遷するとされた「オイラー定数」は、トーラス構造上は0と解釈されます。まぁ、簡単にいうと「コインの表裏が蛇コイルみたいに伸びて合体し対消滅を起こした(従って最終的に一つも残らず)」といったイメージ？
【オイラーの多面体定理と正多面体】「オイラーの多角形定理」と「意味論的統制」概念の導入
オイラー数と曲面の曲がり方の関係を記述する究極の定理 ―ガウス・ボンネの定理―

トーラス(単数形torus,複数形tori)構造自体の内容は単純です。

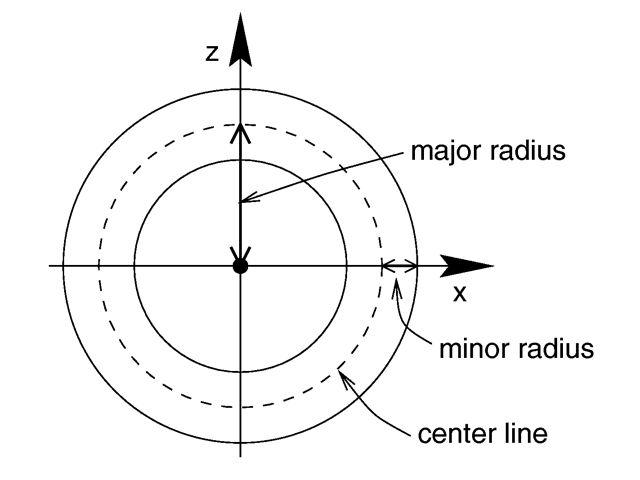
• 小円の半径（Major Radius）…内接円と外接円の差の半分。
• 大円の半径（Minor Radius）…内接円の半径+小円の半径。

ここではこれに円描画関数（Circle Function）Cos(θ)+Sin(θ)(i)の一般形たるCos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)の以下の数値を射影(Projection)する場合を考えてみましょう。

##１辺形(One Side)
式Cos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)でNoS=1の場合。cos(θ-π)＝－cos(θ)なのでこの場合の式はcos(θ)-cos(θ)(i)となる。

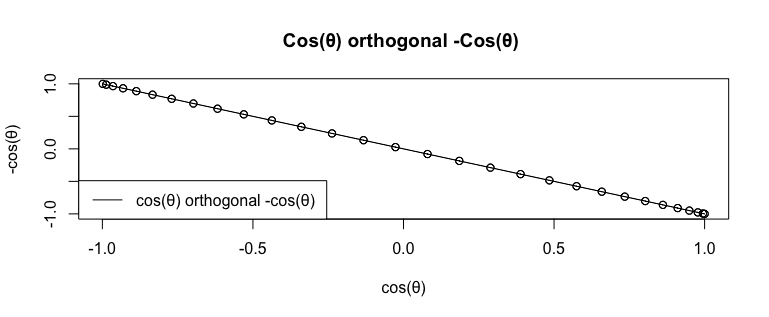
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)*-1
plot(cx,cy,type="o",main="Cos(θ) orthogonal -Cos(θ) ",xlab="cos(θ)",ylab="-cos(θ)")
#凡例
legend("bottomleft", legend=c("cos(θ) orthogonal -cos(θ) "), lty=c(1), col=c(rgb(0,0,0))) 

トーラス構造による表現は不可能だが、1<=NoS<=2の時の振る舞いが2<=NoS<=Infの真逆になる事から**半径１の単位円**(Unit Circle)を基準に考えた場合の**大円の半径**(Major Radius)=1(Inf/Inf),**小円の半径**(Minor Radius)=0(1/Inf)と置いて両者の間にある種の対称性を認める考え方もある。

関数設定

#FHtD=1角形から2角形へ（From Henagon to Digon）
#Noc=角数(Number of corners)
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)

#中心からの補助線
cx0<-rep(0, length=length(cx))
cy0<-rep(0, length=length(cy))
segments(cx0, cy0, cx, cy,col=c(200,200,200))

#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}

1<=Nos<=2の範囲の描画

#アニメーション
library("animation")
Time_Code=seq(1,2, length=30)
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")

##２辺形(Bilateral)
式Cos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)でNoS=2の場合。cos(θ-π/2)＝sin(θ)なのでこの場合の式はcos(θ)+sin(θ)(i)となる。

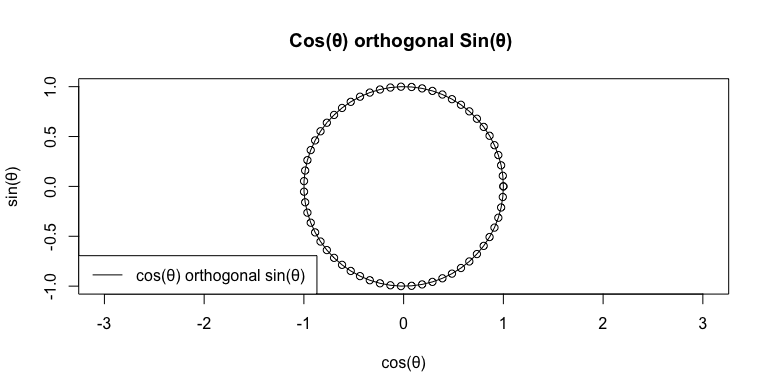
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="o",main="Cos(θ) orthogonal Sin(θ) ",xlab="cos(θ)",ylab="sin(θ)")
#凡例
legend("bottomleft", legend=c("cos(θ) orthogonal sin(θ) "), lty=c(1), col=c(rgb(0,0,0))) 

半径１の単位円(Unit Circle)を基準にトーラス構造を考えた場合、大円の半径(Major Radius)=0,小円の半径(Minor Radius)=1と解釈可能。ところでこの2辺形(Bilateral)、辺の設定が面白い事になってます。

• 円弧上だと(0+1i)系と(0-1i)系の共益複素数(Conjugate complex number)の2本（頂点数2+辺数0(1-1)+面数0で一応はオイラーの多面体定理の立体実在条件を満たす）
• 球表面上だと（ピタゴラスの法則によって取得される「半径と同じ長さの辺数」同様に）円近似上の経度分割数と同数。
  【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源
• ガウスが「1の冪乗の巡回性」を発見して以降、球面や正多面体は主に原蹠と対蹠を定め、その正多面体に外接する球表面の立方対角線(Cubic Diagonal)を設定し、これと垂直に交わる円断面それぞれについてc0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)の構文で正多角形を描いて辺で結ぶアルゴリズムで描かれる様になった（もちろん私のこれまでの投稿も例外ではない）。その大源流はまさにかかる概念(Concept)に由来しているのである。

関数でいうと振動関数-1^x(i^2x)の振る舞いそのもの。
【Rで球面幾何学】等比数列(幾何数列)①その基本的性質について。
【Rで球面幾何学】等比数列(幾何数列)②同心円集合(Concentric Set)に射影(Projection)する準備
【Rで球面幾何学】等比数列(幾何数列)③振動関数を巡る収束と拡散。
【Rで球面幾何学】等比数列(幾何数列)④公比Dが正の場合の収束と拡散, そして対数尺(自然指数関数)

#RD=2角形（Regular Digon）
#Radian=角度（60分割）
RD<-function(Radian){
c0<-seq(0,2*pi,length=60)
c1x<-cos(c0)
c1y<-sin(c0)
plot(c1x,c1y,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Henagon",xlab="cos(θ)",ylab="sin(θ)")

RD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),xlim=c(-1,1),ylim=c(-1,1),main="Regular Henagon",xlab="X",ylab="sqrt(1-X^2) & -sqrt(1-X^2)")

par(new=T)#上書き指定

plot(cx,-1*cy,asp=1,type="l",col=rgb(1,0,0),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")

#緯度(latitude)の描写
lat<-seq(-1,1,length=9)

for(i in lat){
segments(i,f0(i),i,-f0(i),col=c(200,200,200))
}

#経度（Longitude）の描写
lon<-seq(-pi/2,pi/2,length=9)
for(i in lon){

par(new=T)#上書き指定

plot(cx,sin(i)*cy,asp=1,type="l",col=c(200,200,200),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
}
#塗りつぶし

p_max<-15
p0<-seq(pi,0,length=p_max)
px_Hi<-rev(cos(p0))
px_Low<-rev(cos(p0*-1))
py_Hi<-rev(sin(p0))
py_Low<-rev(sin(p0*-1))

#左側インジケータ描画（緑）
polygon(c(px_Hi[1:Radian],px_Low[Radian:1]), #x
c(py_Hi[1:Radian],py_Low[Radian:1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色
#右側インジケータ描画（赤）
polygon(c(px_Hi[p_max:Radian],px_Low[Radian:p_max]), #x
c(py_Hi[p_max:Radian],py_Low[Radian:p_max]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色
}

#アニメーション
library("animation")
Time_Code=c(1:15,14:1)
saveGIF({
for (i in Time_Code){
　RD(i)
}
}, interval = 0.1, movie.name = "RD01.gif")

極座標系における垂直角θや測地法における緯度(Latitude)の様に球表面上の水平断面と組み合わせて任意の位置を指定する座標系においては、かかる変動における往路か復路の半分しか必要としません(半円だけなら-1~0、0~1、1~0、0~-1の4回描いている。そうi^2xだから)。極座標系における水平角φの範囲が2πなのに対し垂直角θの範囲がπだったり、経度が（ロンドンの旧グリニッジ天文台跡を０°とする）東経１８０°と西経１８０°で表されるのに対し、緯度が（赤道を0度とする）北緯90度と南緯90度で表されるのはこの為です。

##幾何学的空間(3角形~6角形)
式Cos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)でNoS=3以上6以下の範囲で広がる例外処理の多い領域。人類が古代より見知って来た幾何学(Geometry)の世界。

様々な要因からNoS=4の場合だけcos(θ)+sin(θ)(i)となります。人類の想像力が2辺形(Bilateral)なる抽象概念に及ぶ様になったのは近世以降。それまではまさにこちらの方が円概念の唯一のイメージ源であり続けてきたのです。
【Rで球面幾何学】何故「正方形」ではCos(θ)+Sin(θ)iが成立するのか？

それ以外にも2^n集、3^n集、5^n集の「立体展開」に関わる例外的特徴/操作が数多く見受けられますが式Cos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)との関係は希薄で、全く別の数理の外挿的影響の結果と考えた方が良さそうです。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

• 2^n集…二辺形(Bilateral),正方形(Square)(外接円/内接円が独自の連続同心円集合を構築する)。
• ３^n集…三角形(Triangle),四面体(Tetrahedron)(Square)(外接円/内接円が独自の連続同心円集合を構築する)
• 5^n集…五角形(Pentagon)
• 2^n3^m集…立方体(Cube),正八面体(Octahedron),六角形(Hexagon)(Square)(外接円/内接円が独自の同心円集合を構築する)
• 2^n3^m5^l集…正十二面体(Dodecahedron),正二十面体(Icosahedron)(Square)(外接円/内接円が独自の同心円集合を構築する)

##5角形(3角形~Pentagon)以上
式Cos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)におけるNoS=5以上Inf未満の場合。もはや幾何学的数理に基づく「立体展開」は見られず、円そのもの(Circle Itself)に至るまで単調な平面展開が続きます。

#アニメーション
library("animation")
Time_Code=c(seq(2,3,length=10),seq(3,6,length=10),seq(6,9,length=10),seq(9,27,length=10),seq(27,71,length=10))
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD05.gif")

ちなみに収束が極めて遅いのでこのアニメーション、段階的に加速させています。

##円そのもの(Circle Itself)
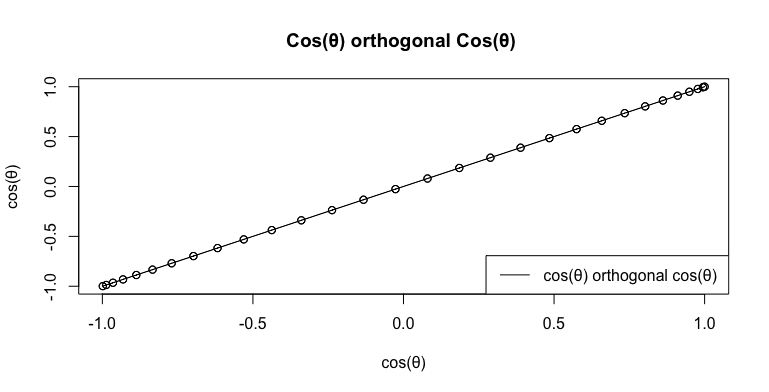
式Cos(θ)+Cos(θ-π/NoS)(i)(NoS=Number of Sides)でNoS=Infの場合。cos(θ-π/Inf)=cos(θ-0)＝cos(θ)なので式はCos(θ)+Cos(θ)(i)となる。

#円そのもの(Circle itself)
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)
plot(cx,cy,type="o",main="Cos(θ) orthogonal Cos(θ) ",xlab="cos(θ)",ylab="cos(θ)")
#凡例
legend("bottomright", legend=c("cos(θ) orthogonal cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))

半径１の単位円(Unit Circle)を基準にトーラス構造を考えた場合、大円の半径(Major Radius)=1(Inf/Inf),小円の半径(Minor Radius)= 0(1/Inf)と解釈可能。

##案外「水と油」の関係にあるトーラス構造の世界(Set)と古典幾何学の世界(Set)

表題で「オイラーの多面体定理との統合」とぶちかました割には完全に竜頭蛇尾な展開となってしまいました。そんな感じで以下続報…