【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…
ここで状態遷移図(State Transition Diagram)上における正多面体(Regular Polyhedron)と正多角形(Regular Polygon)の往復を扱ってますが、それに関連して興味深い概念(Concept)を仕入れました。
オイラー数と曲面の曲がり方の関係を記述する究極の定理 ―ガウス・ボンネの定理―
あらゆる多角形(Polyhedron)において頂点数(Number of Vertexs)と辺数(Number of Edges)は一致する。
すなわち内側に現れる面数(Number of Faces)をカウントしないなら
頂点(Vertex)の数-辺(Edge)の数=0
カウントするなら(常に1と数えて)
頂点(Vertex)の数-辺(Edge)の数+面(Face)の数=1
が成立する。
それならこの2種類の概念をどう使い分けるのか。以下の投稿では以下の形で意味論的統制(Semantic Control)の概念を導入しています。
【Rで球面幾何学】二辺形(Bilateral)と一辺形(One Side)?
比(Ratio)で表現(Expression)可能な有理数(Rational Number)や、それとは別の個別定義(Definition)に頼る無理数(Irrational Number)で構成される「実数の世界(Real Number)」までを「計数可能な世界(Countable Set)」と規定するなら、さらにその先に連続性(Continuity)を見出そうとする「虚理の世界(Imaginary Set)」は「計算自体は可能な世界(Computable Set)」と規定される。もちろんただ計算可能なだけでは与えられた役割を果たせず、それぞれが相応の意味論的統制(Semantic Control)に従わねばならない。
この次元における意味論的統制(Semantic Control)の概念はシンプル極まりなく「(元来は数字導出方法や精度や誤差も添えた)近似や確率の計算結果の集合」を範囲としてきっちり明示しろという事です。例えば以下の様に。
三角関数(Trigonometric Function)の世界
デカルト座標系(Cartesian Coordinate System)」あるいは複素平面(Complex Plane)に射影(Projection)された円そのもの(Circle Itself)を「辺数無限小(1/Inf)辺数無限大(Inf)の多角形」と概念化した近似値計算体系でXY座標(Cos(θ),Sin(θ))あるいは複素数(Complex Number)X+Yiを返す。辺分割数(Nos=Number of Sides)が精度や誤差を規定し、その単位円(Unit Circle=半径1の円弧)の円周長の極限値2πが「実数の世界(Real Number)」に無理数の一つとして加えられる展開を迎えた。
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源

【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似

一辺の長さがAの正n角形に内接する円の半径**R**
- R=A/2*tan(π/n)*cos(π/n)
- A=R2tan(π/n)*cos(π/n)
一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係
1.r=R*cos(π/n)
2.R=r/cos(π/n)
外接円を単位円(Unit Circle)としたのが上記アニメーションとなる。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸(円弧)

XZ軸(Cos波)

YZ軸(Sin波)

自然指数関数/対数関数(Natural Exponential function/Logarithmic Function)の世界
簡単に言うと片対数尺(Semilog Graph)あるいは透視図法(Perspective)の世界。等比数列上の観測原点(Portal)たる1から消失点(Vanishing Point)となる無限大(Inf)もしくは無限小(1/Inf)までの範囲を扱う。
【Rで球面幾何学】等比数列(幾何数列)①その基本的性質について。
【Rで球面幾何学】等比数列(幾何数列)②同心円集合(Concentric Set)に射影(Projection)する準備
【Rで球面幾何学】等比数列(幾何数列)③振動関数を巡る収束と拡散。
【Rで球面幾何学】等比数列(幾何数列)④公比Dが正の場合の収束と拡散, そして対数尺(自然指数関数)

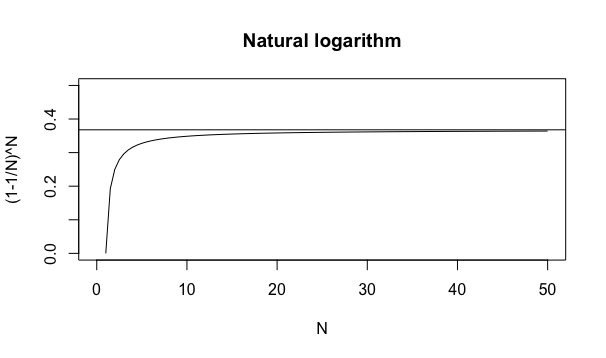
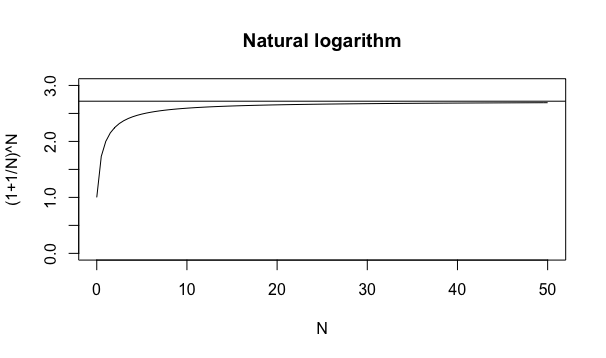
大数学者オイラー(Leonhard Euler,1707年〜1783年)およびその師匠ベルヌーイ(Johann Bernoulli, 1667年〜1748年)は式e^1=(1+1/N)^Nの極限値としてネイピア数e=2.718282…、式e^-1=(1-1/N)^Nの極限値として1/e=0.3678794…を導出。分割数Nが精度や誤差を規定。前者の導出方法が近似論的手法、後者の導出方法が確率論的手法に基づくのが両者の連続性を示唆している。この2つの数も「実数の世界(Real Number)」に無理数の一つとして加えられる展開を迎えた。
【初心者向け】指数・対数関数の発見
2つの「計算自体は可能な世界(Computable Set)」の統合と確率論的世界観の導入(Introduction)
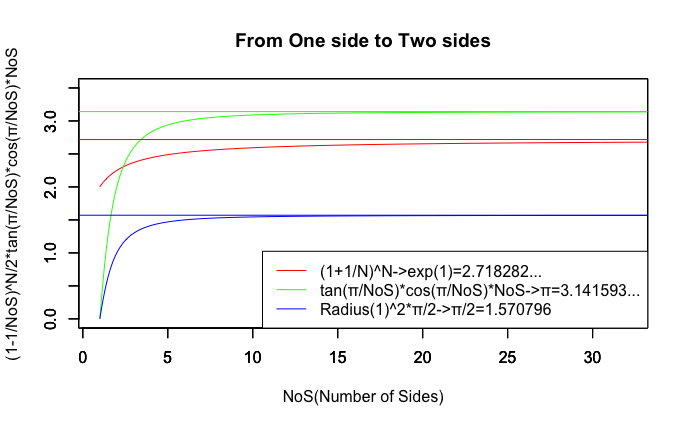
大数学者ガウス(Carolus Fridericus Gauss、1777年〜1855年)は両者の「人類の認識可能範囲外を跋扈する絶対他者」への距離感の取り方に共通性を見出し、これら2つのアプローチが無限遠点においては可換性を備えるとして所謂「ガウス積分」を解いた。
【Rで射影幾何学】そもそも「幾何学」とは何か?
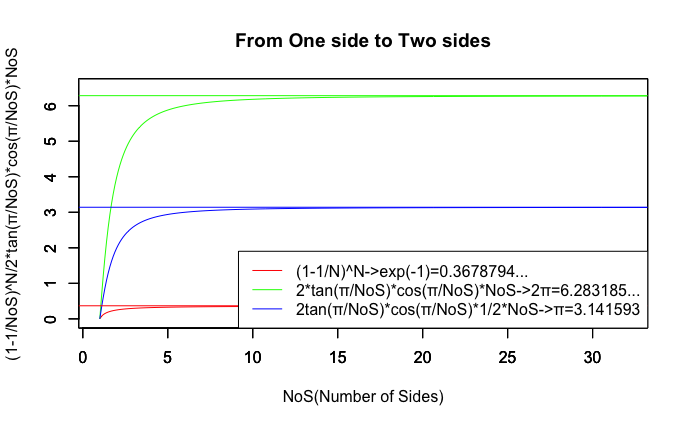
その結果「ベルヌーイの大数の弱法則(The Weak Laws of Large Numbers)」は正規分布概念(Normal Distribution Concept)に発展的に解消され、今日の推計統計学(Inferential Statistic)の基礎が打ち立てられる。逆を言えば、そのあまりの異質性故にこの概念が「実数の世界(Real Number)」の枠内に組み込まれる展開はついぞなかったのである。
【初心者向け】正規分布(Normal Distribution)とは何か?


何となくでも「意味論的統制(Semantic Control)の概念の片鱗くらいは掴めたでしょうか?
- 「オッカムの剃刀」…スコラ哲学者オッカム(William of Ockham、1285年~1347年)が多用した「Pluralitas non est ponenda sine neccesitate(≒Entities shouldn't be necessary=構成要素は必要ない)」すなわち「必要がないなら多くのものを定立してはならない。少数の論理で良いならば、多数の論理を定立してはいけない」なる言い回しに立脚する。
- ウィトゲンシュタイン(Ludwig Josef Johann Wittgenstein、1889年〜1951年)「論理哲学論考(独Logisch-Philosophische Abhandlung、英Tractatus Logico-philosophicus,1918年執筆,1921年初版)」…「語り得ない事については、沈黙するほかない(Wovon man nicht sprechen kann, darüber muss man schweigen.)。」
要するに「オブジェクト指向プログラミングにおいて、参照数が0となったオブジェクトはメモリー上から自動的に消される」みたいな考え方ですね。とりあえず最初の出発点はこれなのです。
そして「幾何学の世界(Geometry Set)」との関係について。
「整数の世界(Integer Number Set)」より素因数分解(Prime Factorization)を経て「多角形や多面体の世界(Polygon & Polyhedron Set)」に至る「幾何学の世界(Geometry Set)」の概念は、こうした流れとは全く系譜が異なります。
【Rで球面幾何学】等差数列(算術数列)① 数直線(Number Line)概念の導入(Introduction)について。
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ

【Rで九九】どうして36個の数字しか使われないのか?
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…
こう考えていくと答えも明白ですね。
- ガウスの発見した「1の冪数の巡回性」の様な純粋に二次元上の問題を扱う際には、面への言及がないのでV-E=0と考えて良い。
- 「オイラーの多面体定理」に関連して多角形と多面体の往復を扱う場合には、面への言及があるのでV-E+F=1と考えて良い。
「オッカムの剃刀」や「ウィトゲンシュタインの論理哲学」や「オブジェクト指向プログラミング上のメモリ管理理論」が、そうあるべきと主張してくる訳です。大体の考え方を学べた時点で、以下続報…