【数理考古学】群論とシミュレーション原理①これまでの投稿内容のまとめ。
吃驚するほどグチャグチャになってしまったので整理を試みます。
三次元トーラスとしての四元数概念導入
リー群の$S_0$空間は実数列(Real Sequence)全体に対応する「一次元トーラス(半径1の単位円=円周群)」、$S_1$空間は複素数列(Complex Sequence)全体に該当する「二次元トーラス(ドーナツ状あるいは円筒状の空間)」に該当します。
【数理考古学】群論とシミュレーション原理⑥二次元トーラス概念への発展
そしてこの考え方の延長線上においてリー群$S_3$空間を四元数集合(Quaternion Set)と対応させるのです。
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか?

- 日本に初めてこの考え方が紹介されたのは明治時代前期の「お雇い外国人」を通じてであり、その時点からすでに加法定理や微積分の概念と結び付けて論じられてきたのです。
四元法(quaternion)と明治前期の日本 : 日本の「高等数学」教育史の一断面 (数学史の研究)
高等数学 (ハヰヱル, マセマチツクス) [四術算及微分積分 (クアトルニャンス, ヱンド, デフヱレンシャル, ヱンド, ヱンテグラル, カルキュラス)
これは「(原点0を半径0の内周円とし、外周円を半径4πとし、直交する大半径の軌道に沿って進む)二次元トーラス座標上の小半径円」にさらに$\cos(θ)+\sin(θ)i$の2自由度を加えた場合に相当します。
円概念(観察結果集合)とオイラーの公式$e^{iθ}$や等比数列$±i^{2x}$(演算結果集合)が等号で結べるのは前者においてネイピア数e=2.718282の近似が十分である場合、後者において周回関数$α^n$の冪根αが十分1に近く、かつ周期関数$β^n$の冪根βが十分-1に近い場合に限られる様に、四元数における操作変数(Instrumental Variables)i,j,kも(中心を巡る周回軌道の状態を保ち続ける為に)ある種の相互従属関係を構築し、これが見た目上の交換法則$x・y=y・x$の放棄(そちらを選ぶと次の升目に進んでしまう選択肢の排除)につながっていくのです。
操作変数法 - Wikipedia
交換法則 - Wikipedia
四元数における操作変数i,j,kが以下の関係にあるのは、そういう理由からなんですね。
複素数
どう計算しても隣の升目にはみ出しません。
i^2=-1\\r(θ)=r±ai\\(a+bi)(c+di)=(ac-bd)+(ad+bc)i
- このうち(ac-bd)の部分がスカラー積=内積となる。
- このうち(ad+bc)の部分がベクトル積=外積となる。
複素数同士の掛算
やはり計算結果が隣の升目にはみ出しません。
α=a+ib,β=c+id\\θ=arg(α),ϕ=arg(β)
と置き、これを極座標上での掛け算に置き換えると以下となる。
α=|α|(\cosθ+i\sinθ)\\β=|β|(\cosϕ+i\sinϕ)\\αβ=|α||β|(\cos(θ+ϕ)+i\sin(θ+ϕ))
四元数
隣の升目にはみ出す選択肢の排除を含みます。
i^2=j^2=k^2=ijk=-1\\r(θ,φ)=r±ai±bj±ck\\(ai+bj+ck)(di+ej+fk)=−1*(ad+be+cf)+(bf−ce)i+(cd−af)j+(ae−bd)k
- このうち(ad+be+cf)の部分がスカラー積=内積となる。
- このうち(bf−ce)i+(cd−af)j+(ae−bd)kの部分がベクトル積=外積となる。
【オイラーの多面体定理と正多面体】正方形における平方対角線と立方体における立方対角線の関係について。
四元数に至る道?
①「原蹠から出発して対蹠に到達しない」あるいは「対蹠から出発して原蹠に到達しない」1頂点操作
まさしく円周角(Circumference Angle)の振る舞い。
【Rで球面幾何学】単位円と単位球②円周角とは何か?
- 円弧そのもの(Circle itself)の特徴に従って「角度0度(0ラジアン)あるいは角度180度(πラジアン)の場合の無限小($\frac{1}{\infty}$)」を最小値、「角度90度($\frac{π}{2}$ラジアン)の場合の直径2」を最大値とする。
- パスカルの三角形1段目「1」に対応。
- 断面0枚。
②「原蹠と対蹠の間を往復する」2頂点操作
これ以降交代級数(Alternating Series)$-1^n$の概念が使える様になります。
-1^n(n=+\infty→-\infty)=(…,-1,1,-1,1,…)
ただし実数範囲にまで視野を広げても均等尺(Even Scale)に従って「0を中心に-1と1(あるいは0と2)の間を往復する」単振動(Simple Vibration)や半径(Radius)/直径(Diameter)の増減が観測されるのみ。

- 1次元の場合、片道2(一巡4)。
- パスカルの三角形2段目「1,1」に対応。
従って対称式(Unit Symmetric)$X+Y=1$の演算結果集合として現れる実軸(Real Axis、一次元の場合1本、二次元の場合直交する2本、3次元の場合直交する3本。ここに現れる直角は「円の中心から伸ばした垂線が円弧と交わる角度」でもある)間において既に三角不等式(Triangle Inequality)$‖x+y‖ \leqq ‖x‖+‖y‖$が成立し、三角比(Trigonometric Ratio)も観測可能であるにも関わらず、これを三角関数(Trigonometric Function)の概念に発展させる事は出来ないのです。
【初心者向け】方形描画関数②距離空間との関係。



【初心者向け】方形描画関数①三角関数との関係。


③実軸(Real Axis)より垂線を伸ばす。
要するにリー群$S_0$(円周群)からリー群$S_1$(二次元トーラス)への拡張です。
- 片道最大$2\sqrt{2}$/最小2(一巡最大$4\sqrt{2}$最小4)
- パスカルの三角形3段目「1,2,1」に対応。
ターレスの定理(Thales's Theorem)により、一対の対蹠と円(ないしは円筒側面)上の任意の点(二次元ピタゴラス群に含まれる任意の元)を結ぶと必ず直角三角形が現れるので、直角自体の検出は容易。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。


- 現段階では通常の直交座標系における線形性とトーラス座標系における線形性の違いが明らかに出来てない成立条件との関係が明らかに出来てない。
そもそも線形ってどういうこと
対称式・交代式と群
④「原蹠から対蹠、あるいは対蹠から原蹠を2回直角に曲がって結ぶ(5回直角に曲がると現点に戻る)」四頂点操作
③を「原蹠から対蹠、あるいは対蹠から原蹠を1回直角に曲がって結ぶ(3回直角に曲がると現点に戻る)」三頂点操作と表現した場合の延長線上に現れる四元数の数理。
- i=j=kの時、片道$3\frac{2}{\sqrt{3}}$(一巡$6\frac{2}{\sqrt{3}}$)。
- パスカルの三角形4段目「1,3,3,1」に対応。
②で正八面体のイメージが現れた様に、ここでは立方体のイメージが現れます。
後者はもっと一般化出来る筈で、その辺りの研究がこれからの課題。
【Rで球面幾何学】正方形における平方対角線と立方体における立方対角線の関係について。



ローラン級数の出番?
もしかしたらこの辺りの話、テイラー展開を特異点を超えて遂行可能としたローラン展開(Laurent Expansion)において登場する「複素数が描く閉曲線の面積の総和は0となる」数理に立脚している事と関係してくるのかもしれません。
物理数学:ローラン展開
ローラン級数のテイラー展開を試す。
$\frac{1}{1-x}$はまぁまぁの収束速度。

$\frac{1}{1+x}$の収束速度は極めて遅い。
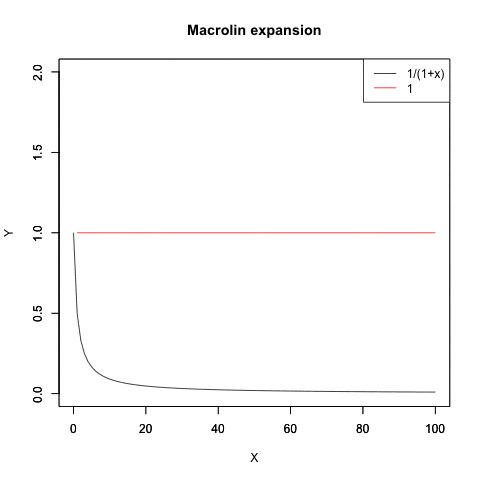

この収束の遅さに業を煮やしてオイラーが考案したのがオイラー変換となる。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?

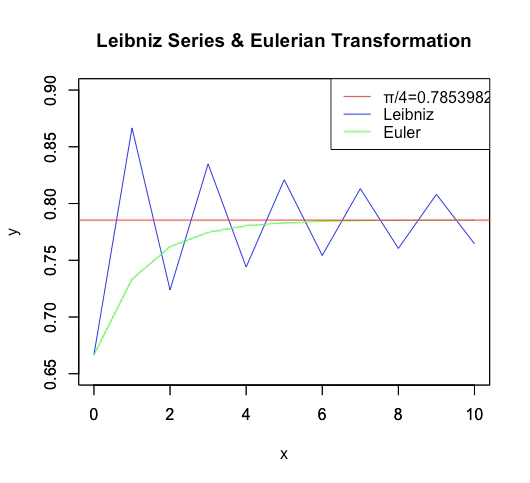
)
そして関数$\frac{1}{z(1−z)}$の原点z0=0の周りでローラン展開

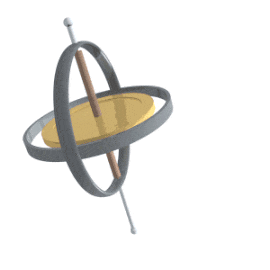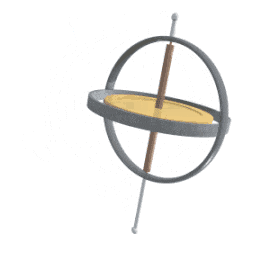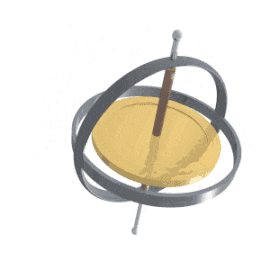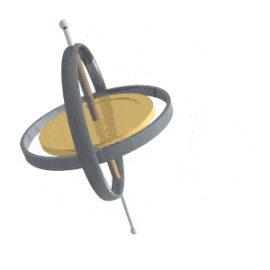
あれ?もしかしたらこの動き、(それ自体は原則として閉じた無限反復運動に過ぎない筈の)複式簿記の記法で対象法人の盛衰を語る管理会計のアプローチ同様、(やはりそれ自体は閉じた無限反復運動の一種に過ぎない筈の)「独楽(こま)の摺漕ぎ運動」を前後左右の水平運動につなげる物理学の記法と何か関係があるの?
歳差 - Wikipedia
「日本初の人工衛星」おおすみも飛ばした四元数原理
再び頭の中がこんがらがってきたので再整理を試みます。
①等速円運動(Constant Velocity Circular Motion)やオイラーの公式(Eulerian formula)$e^{θi}=\cos(θ)+\sin(θ)i$が立脚する「1軸で回転する円状/球状集合」の概念から再出発する。
【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式
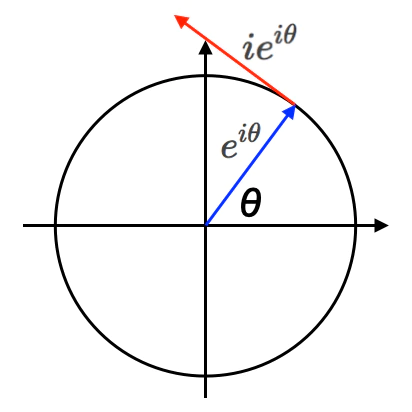
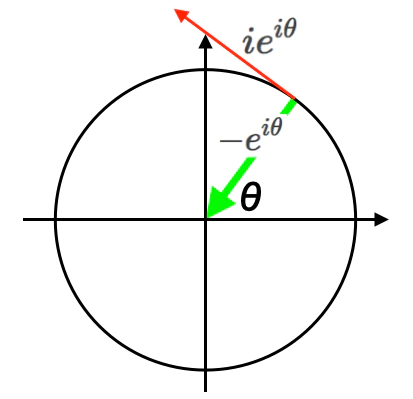
②かかる「1軸で回転する円状/球状集合」に2番目の直行回転軸を与えると、両者の合成結果として3番目の直行回転軸が勝手に追加されるのが三次元トーラス多様体$S_3$=四元数(Quaternion)概念の基本原理といえよう(リー群$S_1$の次が$S_2$でなく$S_3$なのはこの為)。
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか?
ijk=-1の場合

ji-k=-1の場合(iを戻す場合)

ji-k=-1の場合(jを戻す場合)

jki=-1の場合

kj-i=-1の場合

kij=-1の場合

ik-j=-1の場合

一見複雑怪奇に見えますが、これを「トーラスを回転中」あるいは「円筒を直進中」の姿勢制御と捉えると考え方の道筋が見えてきます。
- 上掲の「1周1回転/二分割の二次元トーラス/円筒座標系」を「水平方向に半周する(半周2回で1周する)四元数の軌道」と重ねる。
- すると上掲のトーラス/円筒アニメーションは四元数の公式「$i^2=j^2=k^2=ijk=-1$」のうち「$i^2=-1$」を2回繰り返して元の位置に復帰している場合と重なる(同じ半径の複素数の掛け算は回転角の合計)。ここで複素共益(Complex Conjugate)は回転の向きに該当する。
$(0+1i)^2x$
その複素共益$(0-1i)^2x$
- この考え方に「$j^2=-1$」を直交する追加回転軸として加えるものとする。
$(0+1j)^2x$
その複素共益$(0-1j)^2x$ - するとそれに直交する回転「$k^2=-1$」が自明の場合(Trivial Case)として(ほとんど自動的に)両者を合成したイメージとして勝手に追加されるのである!!
$k=(0+1i)(0-1j)$と考える場合の$k^2=(0+1k)^2=-1$(あるいは$k=(0-1i)(0+1j)$と考える場合の$k^2=(0-1k)^2=-1)
その複素共役としての$k^2=(0-1k)^2=-1$(あるいは$k=(0-1i)(0+1j)$と考える場合の$k^2=(0+1k)^2=-1)
$k=(0+1i)(0+1j)$と考える場合の$k^2=(0+1k)^2=-1$
その複素共役としての$k^2=(0-1k)^2=-1$
なぜ$k=(0+1i)(0−1j)$を「正方向」、$k=(0+1i)(0+1j)$を「負方向」に設定するかというと、デカルト座標系の伝統に従って「右上が+方向である」と考えたがる人類の勝手な都合としか言い様がない。
こうした全体構造を俯瞰すると思い出すのが、日本が初めて打ち上げた人工衛星「おおすみ」を巡る以下のエピソード。
おおすみ - Wikipedia

1970年2月11日に東京大学宇宙航空研究所(後の宇宙科学研究所)が鹿児島宇宙空間観測所からL-4Sロケット5号機により打ち上げた日本最初の人工衛星。その呼称は打ち上げ基地があった大隅半島に由来する。
1966年から観測用ロケットL-3H型に補助ブースターと姿勢制御装置、第4段球形ロケットを追加したL-4Sロケットで打ち上げ実験を開始し、1969年に打ち上げられたL-4T型(L-4Sとほぼ同型であるが、第4段の能力を減じているため、衛星打ち上げ手法の確認は出来ても、軌道投入能力はない)1機の打ち上げを含めた、計5回の試行錯誤の後での打ち上げ成功だった。その結果、日本はソビエト連邦(当時)、アメリカ合衆国、フランスに次いで世界で4番目の人工衛星打上げ国となった。その2ヵ月後に中華人民共和国が東方紅1号の打ち上げに成功し世界で5番目の人工衛星打上げ国となる。
ただ、中国を含め、多くの国は弾道ミサイル開発の副産物として人工衛星打ち上げ技術を習得したのに対し、日本は大学の付属研究所が純粋な民生技術として研究を行い、非軍事目的での人工衛星開発に成功し、なおかつ日本国内では直接的な軍事技術への転用も行われなかったという点で、国際的に特異性を持っている。
ところでL-4Sロケットは誘導制御装置が付いていない、世界初の無誘導衛星打ち上げロケットであった。これは決して開発能力が無かったわけではなく、誘導装置はミサイル開発に繋がる軍事技術への転用が可能であるという指摘が野党の日本社会党やマスコミ等から上がり、開発の着手時期が大幅に遅れたためである(当時の国際的政治状況を考えると、社民党やマスコミは日本より先に人工衛星打ち上げを成功させたい中国共産党の意向を受けてこの様な妨害活動を展開していた可能性がある。「日本共産党の主導権」を巡ってソ連共産党と激しい争い党争を展開していた当時の中国共産党は、劣勢を挽回すべく日本の社民党やマスコミの懐柔工作に傾注しており、その全貌は今日なお明かされていない)。
もちろん、単に真っ直ぐロケットを打ち上げても地球周回軌道には乗らないので、何らかの方法で機体を制御し、地表に対して水平に向きを変えなくては衛星を軌道に投入出来ません。それで代替策として採用された「無誘導重力ターン方式」は、以下のように「手の込んだ」打ち上げ方式だったのです。
- 第1段と第2段は尾翼による空力的効果で、第2段と第3段はスピンモーターにより機体をスピンさせて安定を保つ。
- 第3段燃焼終了・分離後、第3段が第4段に衝突しないように、第3段はレトロモーターで飛翔経路を後落させる。
- 第4段はデスピンモータでスピンを停止、姿勢制御装置で第4段を水平姿勢に制御する。水平姿勢に制御した後、リスピンモーターでスピンを再び掛けて、放物線の頂点で第4段の燃焼を開始する。
「手の込んだ」一例を上げると、デスピンモーターがある。一旦点火をすると燃焼を中断できない固体ロケットによって、ロケット本体のスピンを停めるため、デスピンモーターはスピン方向と反スピン方向の両方にノズルを持っている。デスピンモーターは、燃焼直後には反スピン方向のノズルのみに燃焼経路を開きスピン停止の為の噴射を行うが、スピン停止を検知するとスピン方向のノズルにも燃焼経路を開き、相対推力を零にする。この技術は、後の宇宙研衛星打ち上げロケットに採用されるロール制御モーター「SMRC」に結実する。
ところで、こうした制御方式全体が「回転する独楽(こま)の姿勢制御」からヒントを得て開発されたとされていますが、その独楽(こま)もまた水平方向の回転に対して「軸を傾ける」一軸の追加自由度を備えるだけなのに、その「歳差運動/ジャイロ効果」のタイミング制御によって前後左右方向への水平移動を実現するのであり、これぞまさに四元数におけるijkの関係の由来に他なりません。
歳差 - Wikipedia
独楽の科学 回転する物体はなぜ倒れないのか?
完全に「気分は宇宙飛行士」じゃないですか…そんな感じで以下続報。
























