【数理考古学】群論とシミュレーション原理⑥二次元トーラス概念への発展

【数理考古学】群論とシミュレーション原理①これまでの投稿内容のまとめ。
吃驚するほどグチャグチャになってしまったので整理を試みます。

#一次元トーラス概念の規定

以下で極座標系(Polar Coordinates System)(r,θ)上の円(Circle)=半径1の単位円×半径(Radius)R=観測結果集合とする円周群=リー群$S_0$=1次元トーラス×半径(Radius)rを規定する演算をまとめました。

##ガウスの巡回群

【数理考古学】群論とシミュレーション原理②群導出演算としてのガウスの巡回群

一辺の長さがaの正n角形に外接する円の半径r

• $r=\frac{a}{2\tan(\frac{π}{n})}$
• $a=r(2\tan(\frac{π}{n}))$

一辺の長さがAの正n角形に内接する円の半径R

• $R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
• $A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$

一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係

• $r=Rcos(\frac{π}{n})$
• $R=\frac{r}{cos(\frac{π}{n})}$

外接円を単位円（Unit Circle）としたのが上記アニメーション。

• 外接円の半径Rは単位円の定義に従って1

• これに内接する正多辺形の１辺の長さAは$2\tan(\frac{π}{辺数})\cos(\frac{π}{辺数})$

• 外接円に内接する正多辺形の内接円の半径rは$\cos(\frac{π}{辺数})$

• この場合では円を正n角形の形で分割し「辺数=∞、辺長$\frac{1}{∞}=0$の場合」が円を規定する。その結果として半径1の単位円の場合における円周長として2πが現れ、これを半径rの場合に一般化すると算数段階で習う2πrとなる。

###オイラーの公式

【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式

• $\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}$
• $\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}$

• $e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$
• $\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$

• この場合ではネイピア数e=2.718282の近似が十分な精度以上の場合が円を規定する。

###公比-1の等比数列

【数理考古学】群論とシミュレーション原理⑤群導出演算としての「公比-1の等比数列」

• この場合では「周回関数(Rap Function)$α^n$の冪根αが十分1に近く」かつ「周期関数(Cyclyc Function)$−1^n$の冪根βが十分-1に近い」場合が円を規定する。

#二次元トーラス概念の規定

上掲の円概念の直積(Direct Product)を求めると二次元デカルト座標系(2D Cartesian Coordinate System)ではなく二次元トーラス(2D Torus)なる新たな座標系へと進むことになります。
【Python演算処理】単位球面¥を巡る数理②そして単位トーラスへ - Qiita

とりあえず最初に現れる大半径(Major Radius)Rと小半径(Minor Radius)rの比率が1:1の場合のトーラスを単位トーラス(Unit Torus)と呼び分ける事にしましょう。

• 上図の通り、その側面図には円概念が実軸0を中心として2個隣接して現れる。「実軸0を中心とする半径1の球面」を偶数系(Even System)の起源と置くなら、これが奇数系(Odd System)の起源となる。
  【Python演算処理】単位トーラスを巡る数理②トーラス群の設定
  
  
  

この様に二つの半径の組み合わせで表現されるトーラス座標系(Torus Coordinates System)と三次元デカルト座標系(3D Cartesian Coordinate System)の関係は、一般に媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表されます。

• $R×\cos(t)+r×\cos(p)\cos(t)$
• $R×cos(t)+r×\cos(p)\sin(t)$
• $r×\sin(p)$

一般の円/球面座標系との関係は以下とされています。

• 大半径R=0,小半径r=1の時、単位球面(Unit Sphere=半径1の球表面)を二重に描く(3次元極座標系や経緯度法で垂直角を水平角の半分に取るのは、この時出る重複部分を除く為)。
  【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
  
• 逆に大半径R=1,小半径r=0の時、Z=0となってただの単一の単位円(Unit Circle=半径1の円弧)を描く。かかる極限状態に向かう展開は「単位円に内接する正N角形とそのさらなる内接円の推移(N=∞に近づくほど、どちらの正N角形としての辺長計も円周長2πに限りなく近づいていく)」そのものである。
  

さらにRr比(大半径Rと小半径rの比)に注目すると以下の表現となります。

• トーラスのRr比が$\frac{\infty}{0}=\infty$に限りなく近づく時、その全体構造は上掲の「二重球面状態」に向かう。
• トーラスの Rr比が$\frac{1}{\infty}=0$に限りなく近づく時、その全体構造は上掲の「単円弧状態」に向かう。
• この考え方では「二重球面状態」や「単円弧状態」自体には到達不可能となるので、その結果得られる観測結果集合や演算結果集合はこれらを含まない開集合となる(この事により「二重球面状態」や「単円弧状態」自体は特異点化する)。

どうやらこの景色はn次球面について(人間が扱える)3次元までの空間概念のみ抽出して操作する作業イメージに発展させられそうです。とりあえずこの全体像を無限トーラス(Infinity Torus)と呼ぶ事にしましょう。さらに大半径への分枝切断点追加に際して小半径も同様に分割する場合を元、分割数に比例して回転数も上げていく場合を逆元と置けば、分割数1(追加分枝切断点0)を単位元とする乗法群の一種トーラス群(Torus Group)が現れます。

G_n(n=-\infty→-3→-2→-1→0→1→2→3→+\infty)\\=(\infty,…,4,…,3,…,2,…,1,…,\frac{1}{2},…,\frac{1}{3},…,\frac{1}{4},…,0)

この過程で上面図に現れる正n角形(1分割状態から始まって辺数無限大、辺長無限小の円弧状態に限りなく近づいていく)はRr比によって一意に定まるので、最終的には$±i^{ax}$関数による表現に統合される形となりそうです。
【数理考古学】群論とシミュレーション原理⑤群導出演算としての「公比-1の等比数列」

その一方で、二次元トーラスを平面展開した平坦トーラス(Flat Torus)は1目盛2πの「方眼」が現れますが(分枝点切断前だと)次の升目に移行する概念が存在しません。

【Python演算処理】単位トーラスを巡る数理①平坦トーラスとの往復

• だからComputer RPGのWorld Mapの様にグルグル堂々巡りするのみ。
  RPG世界の形状についての幾何学的考察と可視化
  
• 三次元極座標系(3D Polar Coordinate System)(半径r,水平角φ,垂直角θ)は、ここに現れる二次元トーラス多様体$S_1$というより、むしろ三次元トーラス多様体$S_3$=四元数(Quaternion)上における「縦回転も横回転も伴わない場合(すなわ大半径Rに直交する交点を中心に±Rの線分伸ばした接線の両端を対蹠に取った場合)」がなす球状集合に該当する。
  【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ
  
  
• ここで引いた「補助線」は、等速円運動(Constant Velocity Circular Motion)における速度ベクトルの概念を援用したものである。
  【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式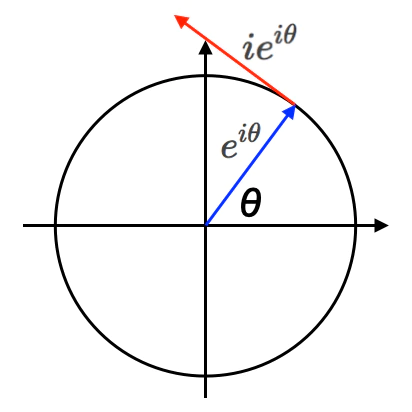
  
  
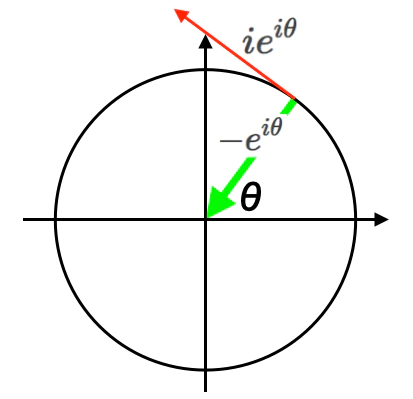
• そして逆をいえば、この球状集合に縦軸と横軸の回転自由度を与えた結果が三次元トーラス多様体$S_3$=四元数(Quaternion)となる訳である。
  【数理考古学】群論とシミュレーション原理⑦三次元トーラスとしての四元数概念導入
  

【数理考古学】群論とシミュレーション原理③群導出演算としての解析学的アプローチ
その考え方の中核は以下の球の表面積を求める式$4πr^2$や球の体積を求める式$\frac{4}{3}πr^3$を導出する三重積分三重積分にあります。
【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復 - Qiita

{\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\ =\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix} \frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\ \frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\ \frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ} \end{vmatrix} drdθdφ }

極座標系(r,φ,θ,…)積分範囲の積み重ね方に注目すると以下となってます。

• まずは角度φ=0→2πφ=0→2πの範囲で積分して円周2πrに到達。
• さらに角度θ=0→πθ=0→πの範囲で積分を重ね**球の表面積****$4πr^2$に到達。
• さらに半径r=0→1r=0→1の範囲で積分を重ね球の体積$\frac{4}{3}πr^3$に到達。

垂直角θ(0~πラジアンのπ範囲)を水平角φ(-πラジアン~0~＋πラジアンの2π範囲)の半分に取るのが特徴で、地球儀上で緯度(±90度)の概念が経度(±180度)の半分で表されるのも同じ数理に基づきます。

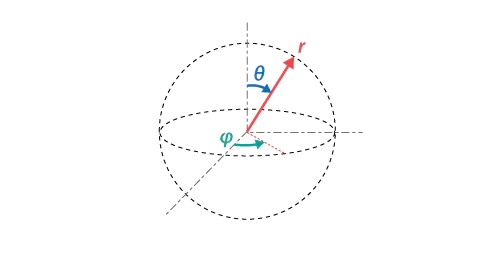
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換

• 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
• $φ=-(\arctan^2(x,y)-\frac{π}{2})$
• $x=r×\cos(φ)$
• $y=r×\sin(φ)$

三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換

• 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
• $φ=-(\arctan^2(x,y)-\frac{π}{2})$
• $θ=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
• $x=r×\sin(θ)\cos(φ)$
• $y=r×\sin(θ)\sin(φ)$
• $z=r×\cos(θ)$

Z軸の座標の取り方についてさりげなく単振動系(Simple Vibration System)$Z_n(n=-1 \rightleftharpoons +1)or(n= 0 \rightleftharpoons 2 )$と三角関数系(Trigonometric Function System)を使い分けていたりします。このズルこそが解析学の解析学たる所以？
神永 正博「超」入門 微分積分 (ブルーバックス) 「微分は下心をもってせよ」

強引に感じた読者も多いと思う。なぜ積分では細部に意味があり、微分では細部を無視しても良いのか。何を無視して何を無視してはいけないか判然としないじゃないか。

この強引さは微積分が「目的」を持っている事からくる。微積分で最も重要なのは目的をかなえられる程度に細部を無視し、近似する事にある。下心を持ちながら、何らかの成果を狙ってやっている事なのだ。

微積分は純粋な興味だけで発展してきた数学ではない。そこに登場する様々な概念や計算技術は理由もなく出てきたものではなく、必ず目的意識が付帯する。体系化された学問とはいえ、実際のところそれは「こう考えたらうまくいった」試行錯誤の結果得られた知恵を編集したものに過ぎないのである。細かい部分が重箱の隅として無視出来るかどうかは「そこからポジティブな成果物が出てくるか」で判断される。要するに成果主義なのである。

• ちなみにプログラムで球面を描画をする際には前者の考え方を使うので、意識して使い分けないと混乱の元になってしまう。
  【Python演算処理】単位球面を巡る数理①とりあえず描画してみる。
  
  
  

そして群論ではこの様なリー群の平面への写像を「(対数写像によって)接空間リー代数(リー環)を取る」と表現するのですが、こちらの系統には複素関数理論における「多価関数への分枝点切断(Branch Point Cut)概念の導入」についての言及がありません。

• かかる2次元トーラス上の回転運動の軌跡は、それをアイロンでも掛けたかの様に真っ直ぐ伸ばし、分岐切断して連続させると(デカルト座標系につながる)円筒座標系(Cylindrical Coordinate System)に推移する訳だが、群論から入るとこの辺りのイメージが掴み難くなってしまうのである。
  
  

一方、複素関数論の系統では、その場合に自明の場合(Trival Case)として選択肢の一つとして現れる「分枝点を2個設定し、目盛のピッチをπとし、偶奇性(Parity)の概念を追加する」考え方への言及がありません。

• 微積分計算上は「分枝点を1個設定し、目盛のピッチを2πとする」選択の一択だからかも？
  【数理考古学】群論とシミュレーション原理③群導出演算としての解析学的アプローチ

そんな感じで以下続報…