【数理考古学】群論とシミュレーション原理①これまでの投稿内容のまとめ。
吃驚するほどグチャグチャになってしまったので整理を試みます。
解析学的アプローチ(Analytical approach)
考え方の中核は以下の球の表面積を求める式$4πr^2$や球の体積を求める式$\frac{4}{3}πr^3$を導出する三重積分三重積分にあります。
【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復 - Qiita
{\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\ =\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix} \frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\ \frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\ \frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ} \end{vmatrix} drdθdφ }
極座標系(r,φ,θ,…)積分範囲の積み重ね方に注目すると以下となってます。
- まずは角度φ=0→2πφ=0→2πの範囲で積分して円周2πrに到達。
- さらに角度θ=0→πθ=0→πの範囲で積分を重ね**球の表面積****$4πr^2$に到達。
- さらに半径r=0→1r=0→1の範囲で積分を重ね球の体積$\frac{4}{3}πr^3$に到達。
垂直角θ(0~πラジアンのπ範囲)を水平角φ(-πラジアン~0~+πラジアンの2π範囲)の半分に取るのが特徴で、地球儀上で緯度(±90度)の概念が経度(±180度)で表されるのも同じ数理に基づきます。
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換
- 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
- $φ(-π \rightleftharpoons +π)=-(\arctan^2(x,y)-\frac{π}{2})$
- $x=r×\cos(φ)$
- $y=r×\sin(φ)$
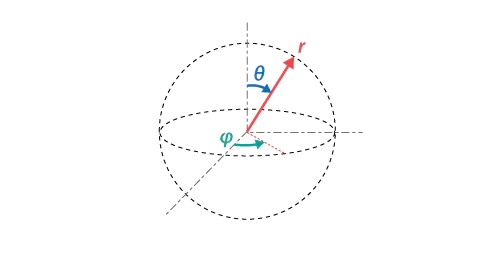
三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
- 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
- $φ(-π \rightleftharpoons +π)=-(\arctan^2(x,y)-\frac{π}{2})$
- $θ(-\frac{π}{2} \rightleftharpoons +\frac{π}{2})=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
- $x=r×\sin(θ)\cos(φ)$
- $y=r×\sin(θ)\sin(φ)$
- $z=r×\cos(θ)$
①導出過程で三角関数の加法定理を使っています。
【初心者向け】「加法定理の幾何学的証明」に挑戦。
- $\cos(α+β)=\cos(α)\cos(β)−\sin(α)\sin(β)$
- $\cos(α−β)=\cos(α)\cos(β)+\sin(α)sin(β)$
- $\sin(α+β)=\sin(α)\cos(β)+\cos(α)\sin(β)$
- $\sin(α−β)=\sin(α)\cos(β)−\cos(α)\sin(β)$
②そしてZ軸の座標の取り方についてさりげなく単振動系(Simple Vibration System)$Z_n(n=-1 \rightleftharpoons +1)or(n= 0 \rightleftharpoons 2 )$と三角関数系(Trigonometric Function System)を使い分けてますね。
【初心者向け】「泳ぐ」数理について。
ある意味このズルさこそが解析学の解析学たる所以なのである。
神永 正博「超」入門 微分積分 (ブルーバックス) 「微分は下心をもってせよ」
強引に感じた読者も多いと思う。なぜ積分では細部に意味があり、微分では細部を無視しても良いのか。何を無視して何を無視してはいけないか判然としないじゃないか。
この強引さは微積分が「目的」を持っている事からくる。微積分で最も重要なのは目的をかなえられる程度に細部を無視し、近似する事にある。下心を持ちながら、何らかの成果を狙ってやっている事なのだ。
微積分は純粋な興味だけで発展してきた数学ではない。そこに登場する様々な概念や計算技術は理由もなく出てきたものではなく、必ず目的意識が付帯する。体系化された学問とはいえ、実際のところそれは「こう考えたらうまくいった」試行錯誤の結果得られた知恵を編集したものに過ぎないのである。細かい部分が重箱の隅として無視出来るかどうかは「そこからポジティブな成果物が出てくるか」で判断される。要するに成果主義なのである。
なるほど…ちなみにプログラムで球面を描画をする際には前者の考え方を使います。この辺り意識して使い分けないと混乱の元になるのですね(正直私もこれに気付くまで混乱し続けた)。
【Python演算処理】単位球面を巡る数理①とりあえず描画してみる。



そんな感じで以下続報。