昨日はデータの種類と線形回帰に触れるところを説明しました。ちょっと出てきた線形回帰というのは回帰分析の一種です。回帰分析と言いますと何やら難しそうな印象がありますが、厳密な数学的な定義は差し置いて、わかりやすく言うとこうなります。
回帰分析とは
たくさんの変数を持つ集まり (= ベクトル) についてある関数にノイズが加わったような状態が事例として観測されました。このときその関数を予測しましょうというのが回帰分析です。
単一の変数 x だけでなく、ふたつの変数 x,y あるいはみっつの変数 x,y,z などを観測して n 個 (n 組) のデータを得る場合、そのデータを 多次元のデータ (multi-dimensional data) と言います。
ここでは 2 次元のデータに絞って考えてみます。 2 次元ですから x と y です。 x と y に区別をもうけず対等に見るのを 相関 (correlation) と言います。 x から y を見るとき 回帰 (regression) と言います。
たとえば年齢と血圧、所得と消費、人口と商業のように、ある一方が他方を左右するという一方向の関係にあるものは分析として回帰分析をとるのが良いでしょう。逆に身長と体重のようにどちらがどちらを決めるという性質にない 2 次元のデータは相関としてとらえることになります。
線形回帰とは
ではこの 2 次元の変数 x と y を考えてみます。この変数間に一方 x が他方 y を左右ないし決定する影響があるとき、 x を 独立変数 (independent variable) 、 Y を 従属変数 (dependent variable) と言います。
この関係式を要約して直線を当てはめるのが線形回帰です。
関数が次の線形モデルでノイズ ε が多変量正規分布の場合
\mathbf{x}'_i=[1,x_{i1},x_{i2},\ldots,x_{im}]^\top
f(\mathbf{x})=\mathbf{\theta}^\top \mathbf{x}'
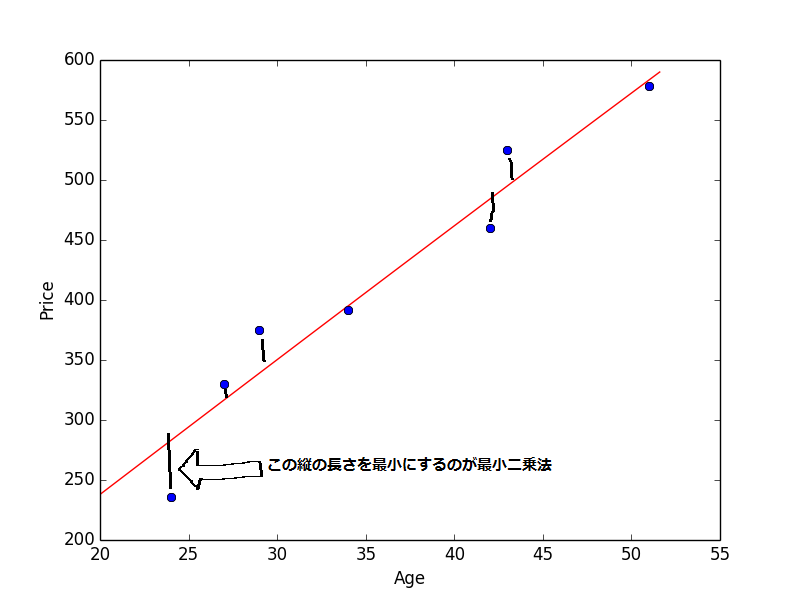
となります。 Θ を最尤推定で求めることは最小二乗法と等価になります。最小二乗法は縦軸 (= Y 軸) の距離のみを最小とするように計算する方法で、回帰分析では特にポピュラーです。
とても汚い図ですが添付します。本当に汚い。
ちなみに最小二乗法は全数をみるので外れ値の影響をダイレクトに受けます。算術平均と同じですね。
線形回帰と検定
線形回帰には要約が生じますから、その傾きや切片に関して信頼区間をともなう検定をおこなうことになります。これにより有意かどうかを調べることができます。
たとえば、不快日数の増加がエアコンの保持率をどれくらい増加させるか、年齢 1 歳の上昇は血圧を何 mmHg 上昇させるか、といった 2 次元データを整理要約して 1 次式が求まれば x から y が決定される様子やしくみがあきらかになります。これが線形回帰です。
回帰と相関の考え方にはつながりがあります。
次回は昨日の例題をもとに、回帰係数と相関関係について考察し、検定を実際におこなってみます。