【Python】NetworkX 2.0の基礎的な使い方まとめ

NetworkXは、グラフ/ネットワーク理論系の計算を行うためのPythonのパッケージです。
最近(2017-09-21)、メジャーアップデートしてバージョン2.0が公開されました。

NetworkX 2.0は1.x系からAPIが大きく整理されています。
これを機に使い方をまとめようと思います。

インストール

pipでインストールしてください。

pip install networkx

古いバージョンをインストール済みなら-Uオプションで更新できます。

pip install -U networkx

グラフの構築

networkx.Graphクラスおよびその派生クラスに頂点と辺を追加していきます。
下の例ではintを頂点としていますが、hashableならなんでも頂点として使えます。

import networkx as nx

G = nx.DiGraph()  # 有向グラフ (Directed Graph)

# 頂点の追加
G.add_node(1)                
G.add_nodes_from([3, 4, 5])

# 辺の追加 (頂点も必要に応じて追加されます)
G.add_edge(1, 2)                                    
G.add_edges_from([(1, 3), (2, 5), (3, 4), (4, 5)])

# 辺の削除
G.remove_edge(3, 4)                    
G.remove_edges_from([(1, 3), (2, 5)])

# 頂点の削除 (削除された頂点に接続されている辺も削除されます)
G.remove_node(5)
G.remove_nodes_from([3, 4])

# 指定したパス上の頂点と辺を追加
nx.add_path(G, [1, 2, 3, 4, 5])  # 1 → 2 → 3 → 4 → 5

# 指定した閉路上の頂点と辺を追加
nx.add_cycle(G, [1, 2, 3, 4, 5])  # 1 → 2 → 3 → 4 → 5 → 1

# 放射状に頂点と辺を追加
nx.add_star(G, [1, 2, 3, 4, 5])  # 1 → 2, 1 → 3, 1 → 4, 1 → 5

グラフの可視化

グラフの可視化には、Matplotlibを使う方法とPyGraphvizを使う方法があります。
設定可能な項目が多いのでこの記事では軽い説明に留めます。

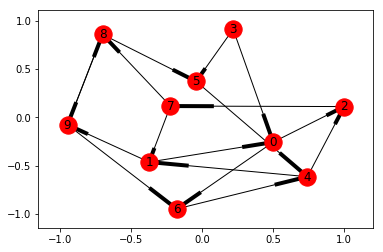
Matplotlibを使う

Matplotlibを使う方法の利点は、インストールが簡単なことです。
欠点は曲線的な辺を描画してくれないことで、複雑なグラフになると頂点や辺やラベルが盛大に重なります。長いラベルをつけるのには向いていません。

import matplotlib.pyplot as plt
import networkx as nx

G = nx.DiGraph()
nx.add_path(G, [3, 5, 4, 1, 0, 2, 7, 8, 9, 6])
nx.add_path(G, [3, 0, 6, 4, 2, 7, 1, 9, 8, 5])

nx.draw_networkx(G)
plt.show()

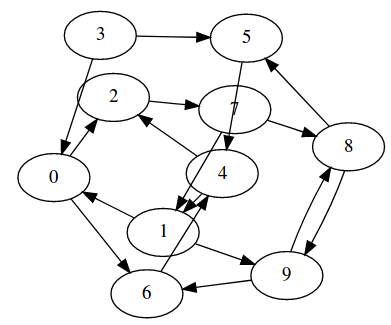
PyGraphvizを使う

PyGraphvizを使うと、Matplotlibを使うよりも気の利いた見た目になります。
欠点は、WindowsにPyGraphvizをインストールするのが多少面倒なことです。
Ubuntuなら apt install graphviz libgraphviz-dev して pip install pygraphviz でOK。

インストール手順（Windows）

1. Graphvizをインストールする。（ http://wingraphviz.sourceforge.net/wingraphviz/ ）
2. Githubで公開されているビルド済みwheelを使ってPyGraphvizをインストールする。

# Python 3.6
pip install "https://github.com/CristiFati/Prebuilt-Binaries/blob/master/PyGraphviz/v1.5/Graphviz-2.42.2/pygraphviz-1.5-cp36-cp36m-win_amd64.whl?raw=true"

# Python 3.7
pip install "https://github.com/CristiFati/Prebuilt-Binaries/blob/master/PyGraphviz/v1.5/Graphviz-2.42.2/pygraphviz-1.5-cp37-cp37m-win_amd64.whl?raw=true"

# Python 3.8
pip install "https://github.com/CristiFati/Prebuilt-Binaries/blob/master/PyGraphviz/v1.5/Graphviz-2.42.2/pygraphviz-1.5-cp38-cp38-win_amd64.whl?raw=true"

（参考：Installing pygraphviz on Windows 10 64-bit, Python 3.6）

使い方

import networkx as nx

G = nx.DiGraph()
nx.add_path(G, [3, 5, 4, 1, 0, 2, 7, 8, 9, 6])
nx.add_path(G, [3, 0, 6, 4, 2, 7, 1, 9, 8, 5])

nx.nx_agraph.view_pygraphviz(G, prog='fdp')  # pygraphvizが必要

Jupyter Notebookを使っている場合は、SVGで表示することができます。

import networkx as nx
from IPython.display import SVG, display

G = nx.DiGraph()
nx.add_path(G, [3, 5, 4, 1, 0, 2, 7, 8, 9, 6])
nx.add_path(G, [3, 0, 6, 4, 2, 7, 1, 9, 8, 5])

svg = SVG(nx.nx_agraph.to_agraph(G).draw(prog='fdp', format='svg'))
display(svg)

基本的な情報の取得

この辺は1.xから変更が多いようです。

import matplotlib.pyplot as plt
import networkx as nx

G = nx.DiGraph()
nx.add_cyle(G, [1, 2, 3, 4, 5])
nx.add_star(G, [1, 2, 3, 4, 5])

# 頂点の一覧
print(list(G.nodes))
# [1, 2, 3, 4, 5]

# 辺の一覧
print(list(G.edges))
# [(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (3, 4), (4, 5), (5, 1)]

# 指定した始点に対する、終点の一覧と辺の一覧
print(list(G.succ[1]), G.out_edges(1))
# [2, 3, 4, 5] [(1, 2), (1, 3), (1, 4), (1, 5)]

# 指定した終点に対する、始点の一覧と辺の一覧
print(list(G.pred[5]), G.in_edges(5))
# [4, 1] [(4, 5), (1, 5)]

# 指定した頂点に対する、隣接している頂点の数とその一覧
print(G.degree(4), list(nx.all_neighbors(G, 4)))
# 3, [3, 1, 5]

頂点や辺にデータをもたせる

G.nodesとG.edgesは、頂点および辺をキー、その属性値の辞書を値とした、Mapping (辞書っぽいオブジェクト) になっています。
さらにG.succはネストしたMappingになっており、辺の始点→終点→属性辞書の順に辿ることができます。同様にG.predは辺の終点→始点→属性辞書の順に辿ることができます。

import matplotlib.pyplot as plt
import networkx as nx

G = nx.DiGraph()
G.add_edges_from([(1, 2), (1, 3), (2, 3)])

# G.nodes[頂点][属性キー] = 属性値
G.nodes[1]['a'] = 'Alice'

# G.edges[辺][属性キー] = 属性値
G.edges[1, 2]['b'] = 'Bob'

# G.succ[始点][終点][属性キー] = 属性値
G.succ[2][3]['c'] = 'Carol'

# G.pred[終点][始点][属性キー] = 属性値
G.pred[3][1]['d'] = 'Dave'

print(dict(G.nodes))
# {1: {'a': 'Alice'}, 2: {}, 3: {}}

print(dict(G.edges))
# {(1, 2): {'b': 'Bob'}, (1, 3): {'d': 'Dave'}, (2, 3): {'c': 'Carol'}}

print(G.succ)
# {1: {2: {'b': 'Bob'}, 3: {'d': 'Dave'}}, 2: {3: {'c': 'Carol'}}, 3: {}}

print(G.pred)
# {1: {2: {'b': 'Bob'}, 3: {'d': 'Dave'}}, 2: {3: {'c': 'Carol'}}, 3: {}}

nx.set_node_attributes()やnx.get_edge_attributes()を使うと属性値をまとめて取得したり設定したりできます。

import networkx as nx

G = nx.DiGraph()
G.add_edges_from([(1, 2), (1, 3), (2, 3)])

# すべての頂点に同じ属性値を設定する.
nx.set_node_attributes(G, name='a', values='Alice')

# 頂点ごとに属性値を個別に設定する. キーは共通.
nx.set_node_attributes(G, name='b', values={2: 'Bob', 3: 'Bravo'})

# まるごと渡す.
nx.set_node_attributes(G, values={1: {'c': 'Carol'}, 2: {'d': 'Dave'}})

print(nx.get_node_attributes(G, 'b'))
# {2: 'Bob', 3: 'Bravo'}

print(nx.get_node_attributes(G, 'c'))
# {2: 'Carol'}

print(dict(G.nodes))
# {1: {'a': 'Alice', 'c': 'Carol'}, 2: {'a': 'Alice', 'b': 'Bob', 'd': 'Dave'}, 3: {'a': 'Alice', 'b': 'Bravo'}}

探索系の関数

import matplotlib.pyplot as plt
import networkx as nx

G = nx.DiGraph()
nx.add_cyle(G, [1, 2, 3, 4, 5])
nx.add_star(G, [1, 2, 3, 4, 5])

# 2点間の最短経路
print(nx.shortest_path(G, source=2, target=1))
# [2, 3, 4, 5, 1]

# 指定した点から各点への最短経路
print(nx.shortest_path(G, source=2))
# {1: [2, 3, 4, 5, 1], 2: [2], 3: [2, 3], 4: [2, 3, 4], 5: [2, 3, 4, 5]}

# 各点から指定した点への最短経路
print(nx.shortest_path(G, target=1))
# {1: [1], 2: [2, 3, 4, 5, 1], 3: [3, 4, 5, 1], 4: [4, 5, 1], 5: [5, 1]}

# 各点から各点への最短経路
print(nx.shortest_path(G))
# ...

# ゴール地点までの最短経路長が、ある長さ未満に収まるスタート地点とその経路
print(nx.single_target_shortest_path(G, target=1, cutoff=2))
# {1: [1], 4: [4, 5, 1], 5: [5, 1]}

# スタート地点からの最短経路長が、ある長さ未満に収まるゴール地点とその経路
print(nx.single_source_shortest_path(G, source=3, cutoff=2))
# {3: [3], 4: [3, 4], 5: [3, 4, 5]}

# スタート地点からゴール地点までのすべての単純路 (同じ頂点を通らないパス)
print(list(nx.all_simple_paths(G, source=1, target=5)))
# [[1, 2, 3, 4, 5], [1, 3, 4, 5], [1, 4, 5], [1, 5]]

さいごに

他にも1.xからの変更点がいろいろとあるようです。
暇を見つけてちょこちょこ更新していこうと思います。