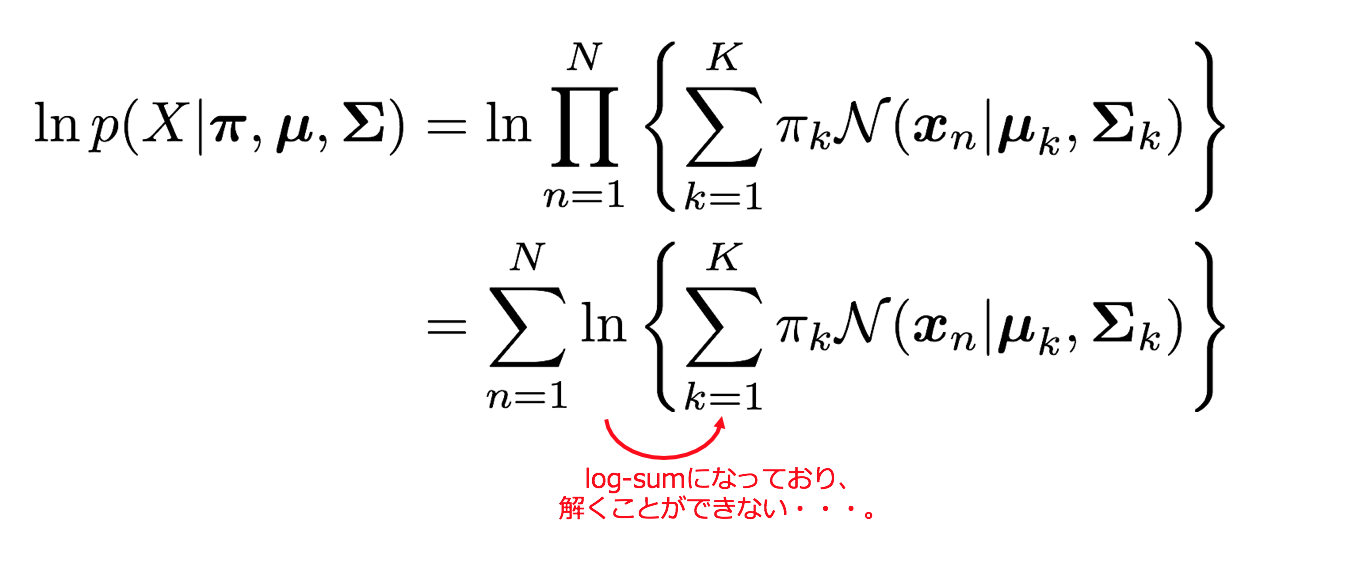数学とコンピュータAdvent Calendar 2017

EMアルゴリズム徹底解説

Last updated at 2024-09-03Posted at 2017-12-23

こんにちは、DeNAでデータサイエンティストをやっているまつけんです。

本ブログは、混合ガウス分布を題材に、EMアルゴリズムという機械学習界隈では有名なアルゴリズムを丁寧に解説することを目的として書いています。

また、この記事は、「数学とコンピュータ Advent Calendar 2017」の24日目の記事です。
そして長いです。

1. はじめに

観測した確率変数 $X$ をよく表現する、モデル $p(x|\theta)$ のパラメータを求めることが確率分布の推定ではよく行われます。つまり最尤法ですね。より複雑な分布になるとその分布の構造に潜在変数(Latent Variable) $Z$ があると仮定してモデル化を行うと、シンプルな組み合わせで $X$ の分布を表現できることがあります。今回扱う混合ガウス分布もその一つです。

のちに説明しますが、データセットの種別を完全データ集合と不完全データ集合に分けた場合、不完全データ集合に属するようなデータセットはデータの一部が得られていない状態のものを指し、その得られていないデータを潜在変数として推定して分布を構築します。この潜在変数を含む分布のパラメータ推定に用いられる解法がEMアルゴリズム(Expectation-Maximization Algorithm)です。

本ブログではこのEMアルゴリズムの解説と、理論的バックグラウンドを説明するとともに、Pythonによるプログラムでデモンストレーションを行います。

以下、こちらの目次に従って説明をしていきます。
2.　k−meansによるクラスタリング
3.　EMアルゴリズムによる混合ガウス分布の推定
4.　一般のEMアルゴリズム
5.　混合ガウス分布推定の解釈

2. k−meansによるクラスタリング

2−1. k-meansの概要

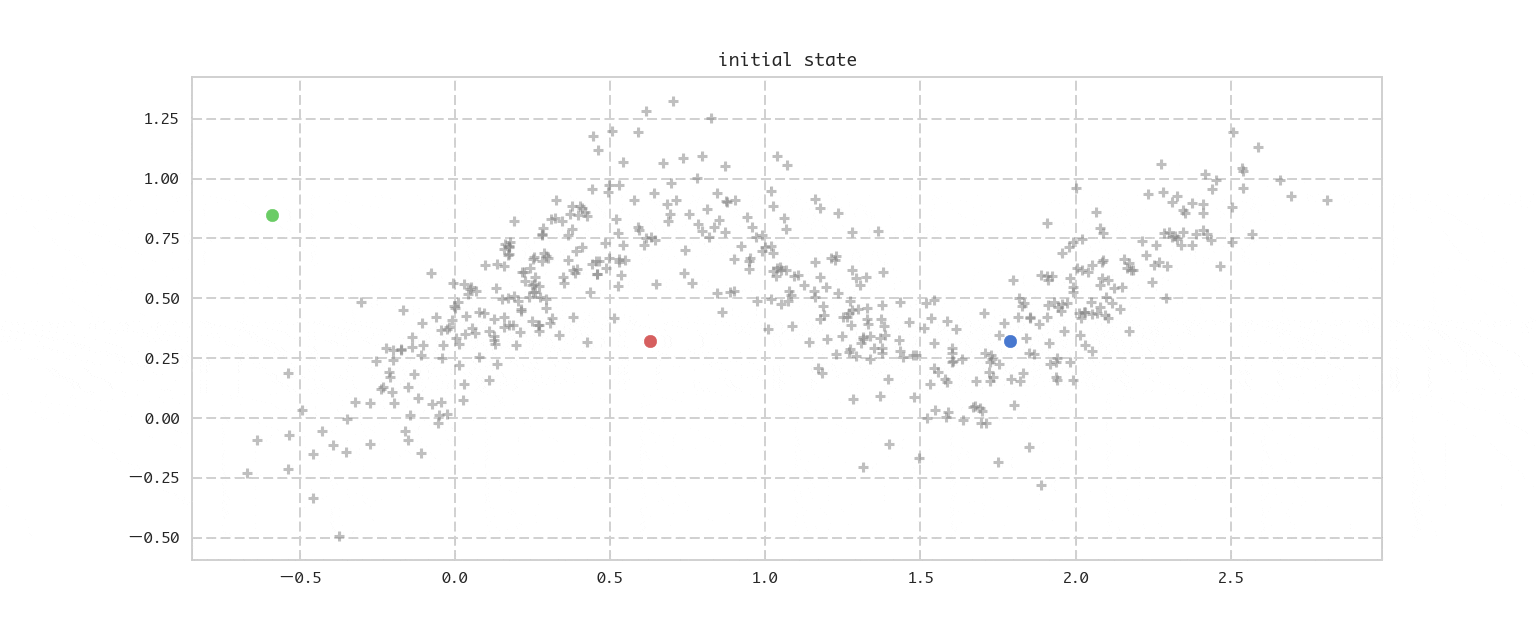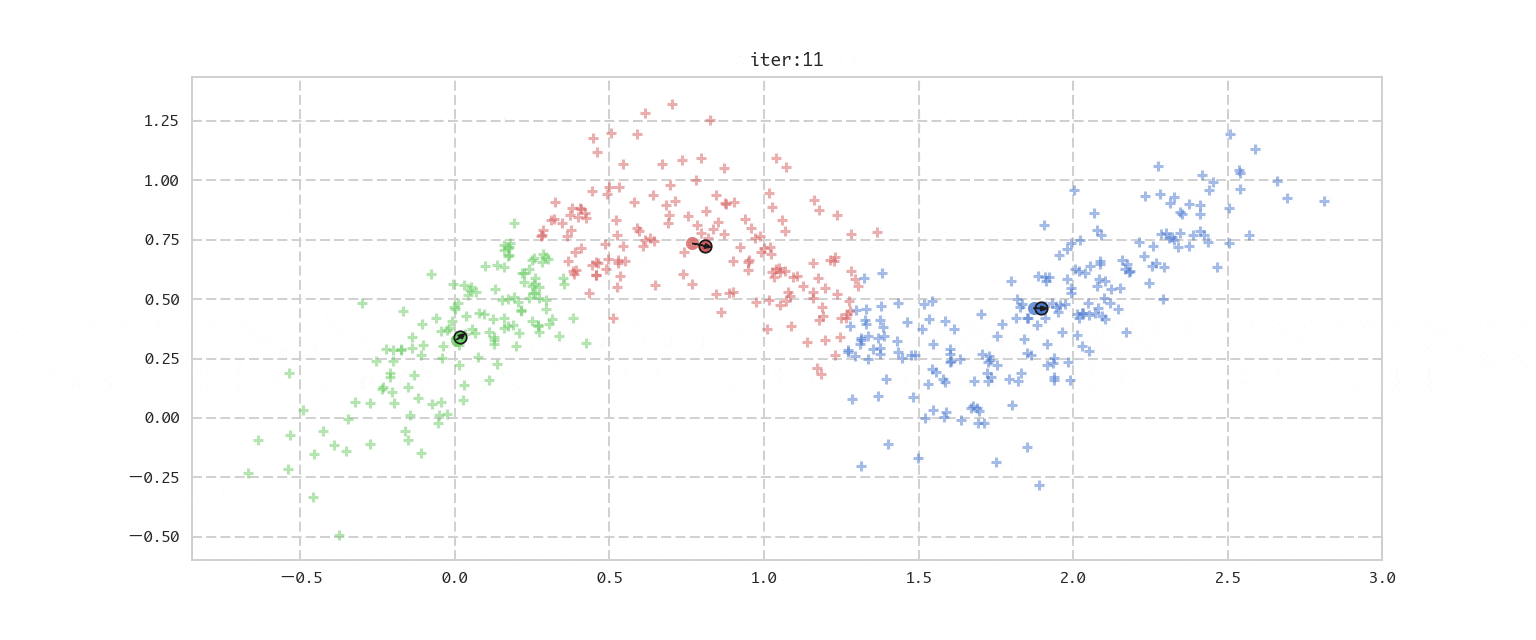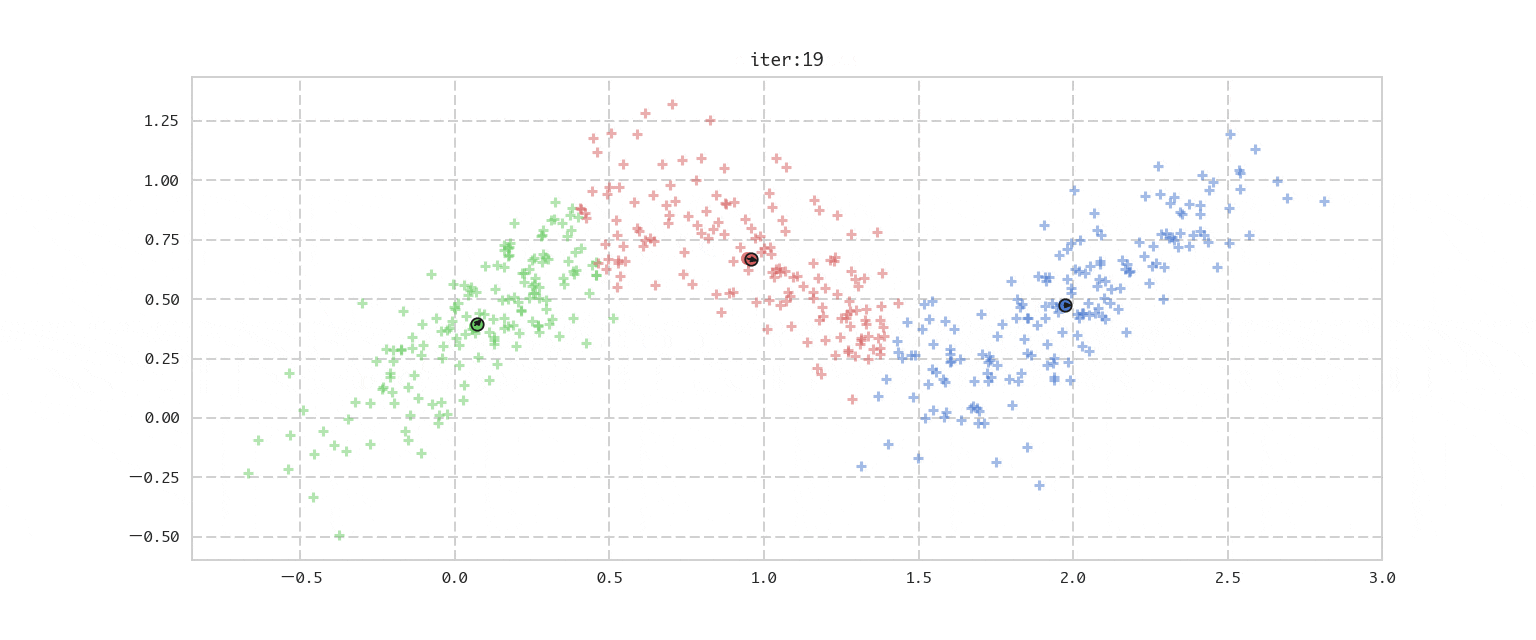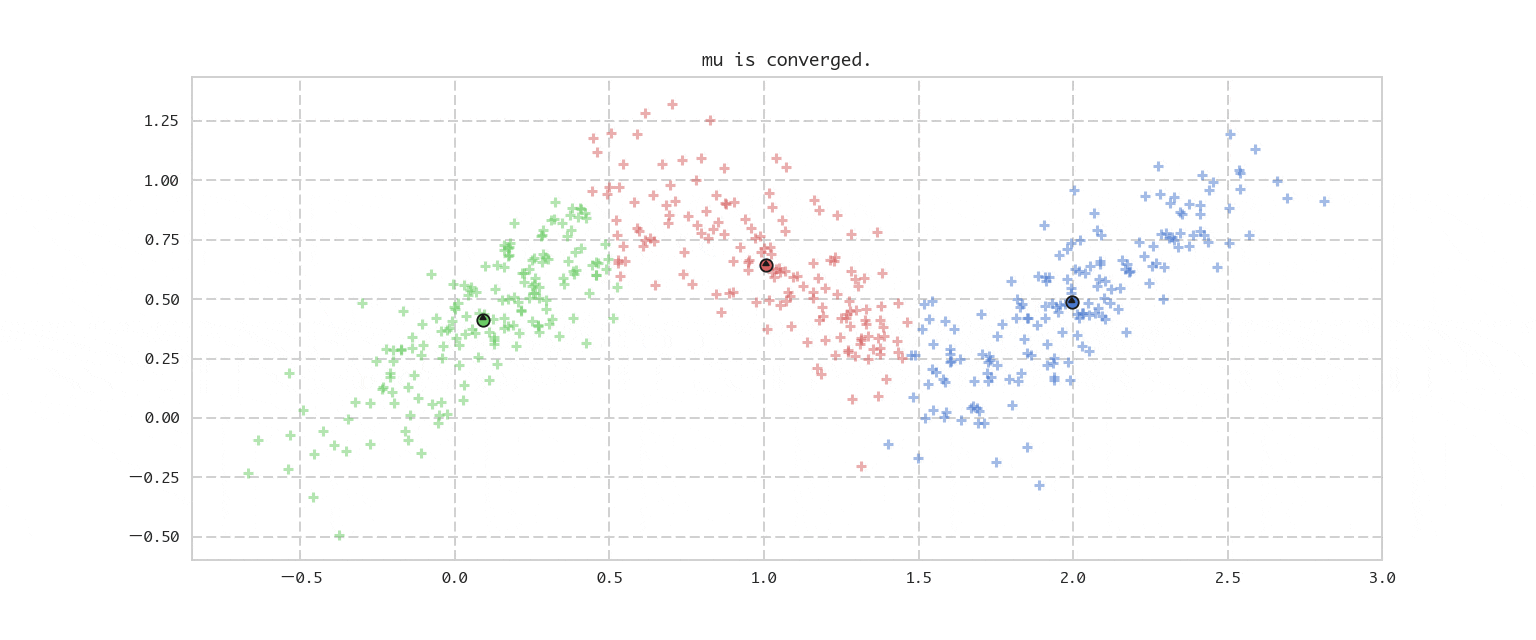
今回の推定ターゲットである混合ガウス分布はデータのクラスタリングに利用できますが、その前にその特殊ケースとして確率を用いないアプローチであるk−meansを先に解説します。これは得られたデータをデータ同士の近さを基準にK個（Kはハイパーパラメーターとして与える）のクラスタに分割する手法です。先にイメージをアニメーションでお伝えすると下記になります。

図1： k-meansによるクラスタの推定の流れ

アルゴリズムの概略は以下の通りです。$K=3$, データの次元$D=2$、データの数$N=500$を例にとります。

クラスターの中心（Centroidともいう）を表す ${\boldsymbol\mu}$ をクラスタ数$K=3$個用意し、適当に初期化する。(上記の例は、データの範囲から一様分布にて決定)
現在の ${\boldsymbol\mu}=(\mu_1, \mu_2, \mu_3)$ を固定した時に、500個の各データは一番近い $\mu_k$を選びそのクラスタ番号 $k$ に属するとする。
各クラスタ $k$ に属するデータの平均を求め、それを新しいクラスターの中心として ${\boldsymbol\mu}$ を更新する。　
${\boldsymbol\mu}$ の更新の差分を調べ、変化がなくなれば収束したとして終了。更新差分があれば2.に戻る。

2−2. 導出

さて、上記のアルゴリズムがなぜ導出されたかというと、とある損失関数を定義して、それの最小化を行う過程で導出されます。
まず、ここで使用する記号について記載します。

$x$ : $D$次元のデータ
$\mathcal{D}=｛x_1,\cdots, x_N｝$ : $N$個の観測点（データ集合）
$K$ : クラスタの数（既知の定数）
$\mu_k (k=1,\cdots, K)$ : $D$次元のCentroid(クラスタの中心を表す)
$r_{nk}$ : $n$個目のデータがクラスタ$k$に属していれば$1$を、そうでなければ$0$をとる２値の指示変数

損失関数 $J$ を下記のように定義します。

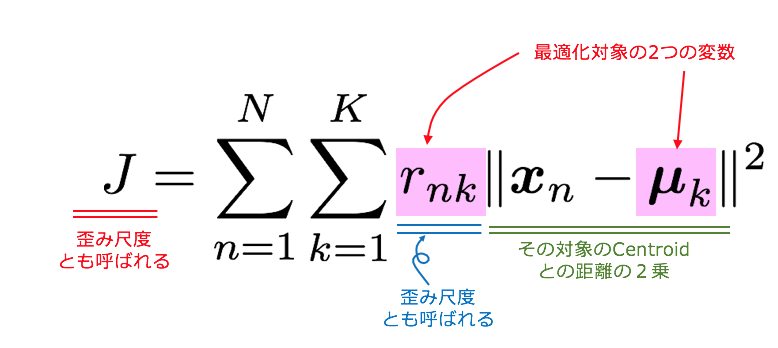
この損失関数$J$を下記２ステップで最小化します。

ステップ１.　$\mu_k$を固定して$J$を$r_{nk}$で偏微分して最小化
ステップ２.　$r_{nk}$を固定して$J$を$\mu_k$で偏微分して最小化

ステップ１
$\mu_k$を固定して$J$を$r_{nk}$で偏微分して最小化します。
$d_{nk}=|| x_n - \mu_k ||^2$とおくと、

J = \sum_n (r_{n1} d_{n1} + r_{n2} d_{n2} + \cdots + r_{nk} d_{nk})

なので、データ1つ1つに対して$(r_{n1} d_{n1} + r_{n2} d_{n2} + \cdots + r_{nk} d_{nk})$を最小にすればよく、$r_{nk}$が２値指示変数であることを考えると、それは$ d_{n1}, d_{n2} , \cdots , d_{nk}$の中で一番小さい$d_nk$を選べば良いので、

  r_{nk} = \left\{ \begin{array}{ll}
    1 & (k = \arg \min_j || x_n - \mu_k ||^2) \\
    0 & (otherwise)
  \end{array} \right.

ステップ2
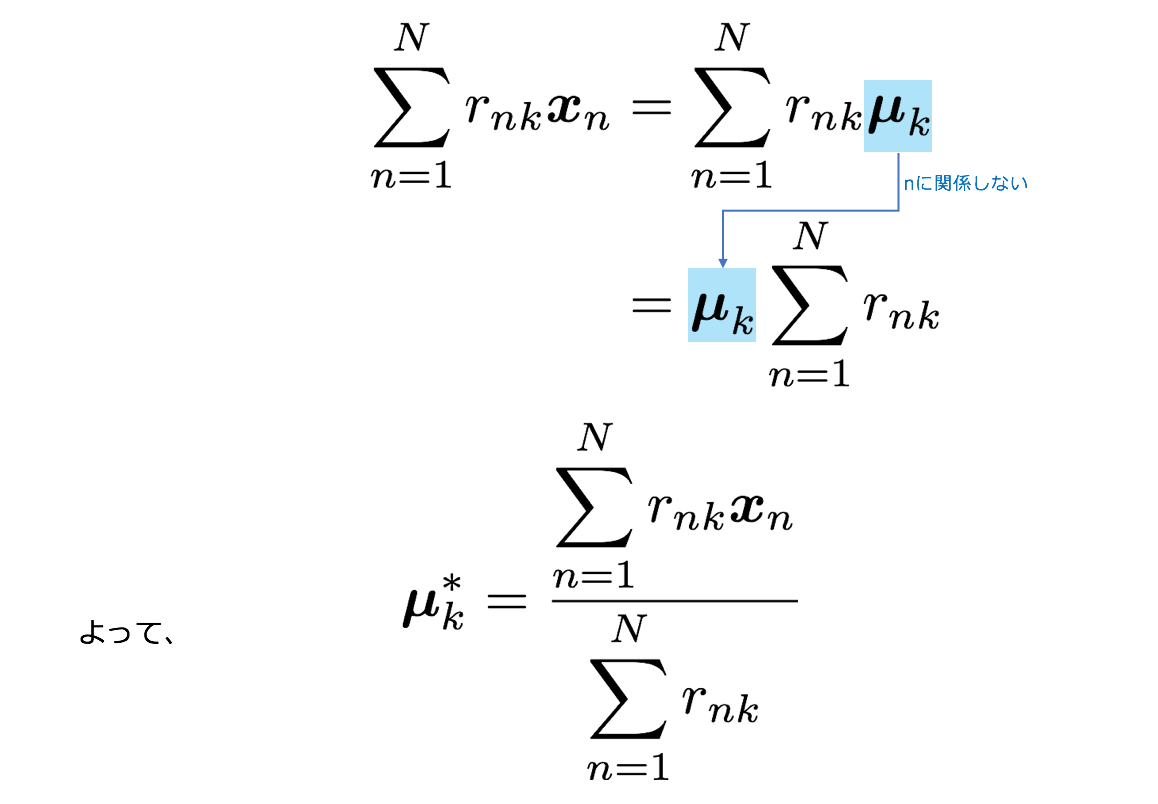
$r_{nk}$を固定して$J$を$\mu_k$で偏微分して最小化します。

式変形をすると、

クラスタ$k$の最適なCentroidは上記のように、クラスター$k$に所属しているデータの平均であることがわかりました。

上記より最初のデモンストレーションで行っていたアルゴリズムは損失関数$J$の最適化によって導出されたものを適用していたことがわかります。

2−3. 実装

上記で示した２ステップを計算して、イテレーションを回すだけのシンプルなプログラムです。最後に更新前のmuと更新後のmuの差を取り、それがある程度小さくなったら収束したと判断し、イテレーションを止めるようにしています。

下記はアルゴリズム部分の抜粋です。プログラムの全文はコチラにあります。

k-means抜粋

for _iter in range(100):
    # Step 1 ====================================================================
    # calculate nearest mu[k]
    r = np.zeros(N)
    for i in range(N):
        # 各データごとにCentroidとの距離を計算し、一番小さいkをrに割り当てる
        r[i] = np.argmin([np.linalg.norm(data[i]-mu[k]) for k in range(K)])

    # Step 2 ====================================================================
    cnt = dict(Counter(r))
    N_k = [cnt[k] for k in range(K)]
    mu_prev = mu.copy()
    # kごとにデータの平均をとりmuに代入
    mu = np.asanyarray([np.sum(data[r == k],axis=0)/N_k[k] for k in range(K)])
    diff = mu - mu_prev
    print('diff:\n', diff)

    # visualize ====================================================================
    plt.figure(figsize=(12,8))
    for i in range(N):
        plt.scatter(data[i,0], data[i,1], s=30, c=color_dict[r[i]], alpha=0.5, marker="+")

    for i in range(K):
        ax = plt.axes()
        ax.arrow(mu_prev[i, 0], mu_prev[i, 1], mu[i, 0]-mu_prev[i, 0], mu[i, 1]-mu_prev[i, 1],
                  lw=0.8,head_width=0.02, head_length=0.02, fc='k', ec='k')
        plt.scatter([mu_prev[i, 0]], [mu_prev[i, 1]], c=c[i], marker='o', alpha=0.8)
        plt.scatter([mu[i, 0]], [mu[i, 1]], c=c[i], marker='o', edgecolors='k', linewidths=1)
    plt.title("iter:{}".format(_iter))
    plt.show()
    
    if np.abs(np.sum(diff)) < 0.0001:
        print('mu is converged.')
        break

3. EMアルゴリズムによる混合ガウス分布の推定

3−1. 混合ガウス分布の概要

ここからが本ブログ記事の本番です。
下記にEMアルゴリズムによる混合ガウス分布(Gaussian Mixture Model:GMM)の推定のイテレーションの様子をアニメーションにしたものを掲載しました。k-meansの時は、各データはどこかのクラスタ１つに所属していました。なので、$r_1 = (0, 1, 0)$のように0-1の指示変数できっちりと分けていました。

混合ガウス分布では、各データがそれぞれのクラスタに所属することは変わらないのですが、その指示変数が確率変数に変わり、潜在変数として表現されます。そのため、例えば1つ目のデータ$x_1$に対応する潜在変数の$z_1$期待値をとると例えば$E[z_1]=(0.7, 0.2, 0.1)$のように$0\leq z_{1k} \leq 1$の範囲の値をとるようになります。それを下記の図ではグラデーションで表現しています。

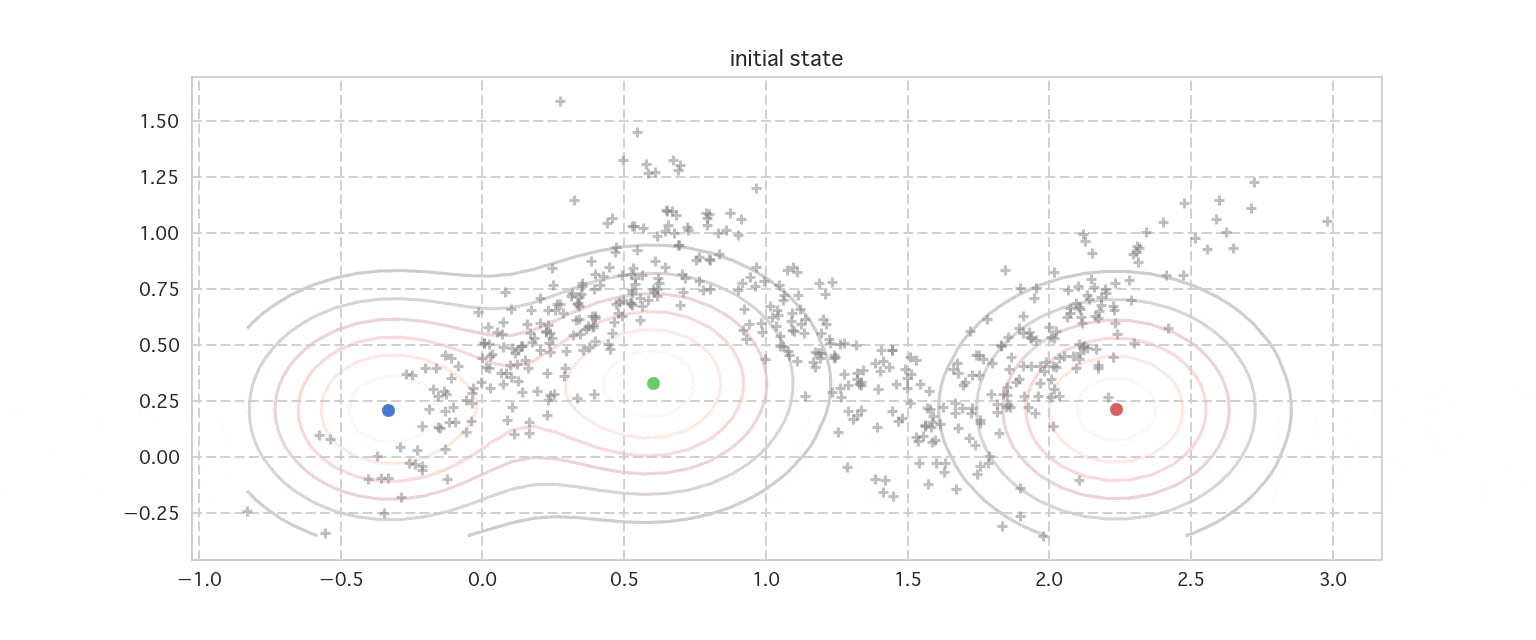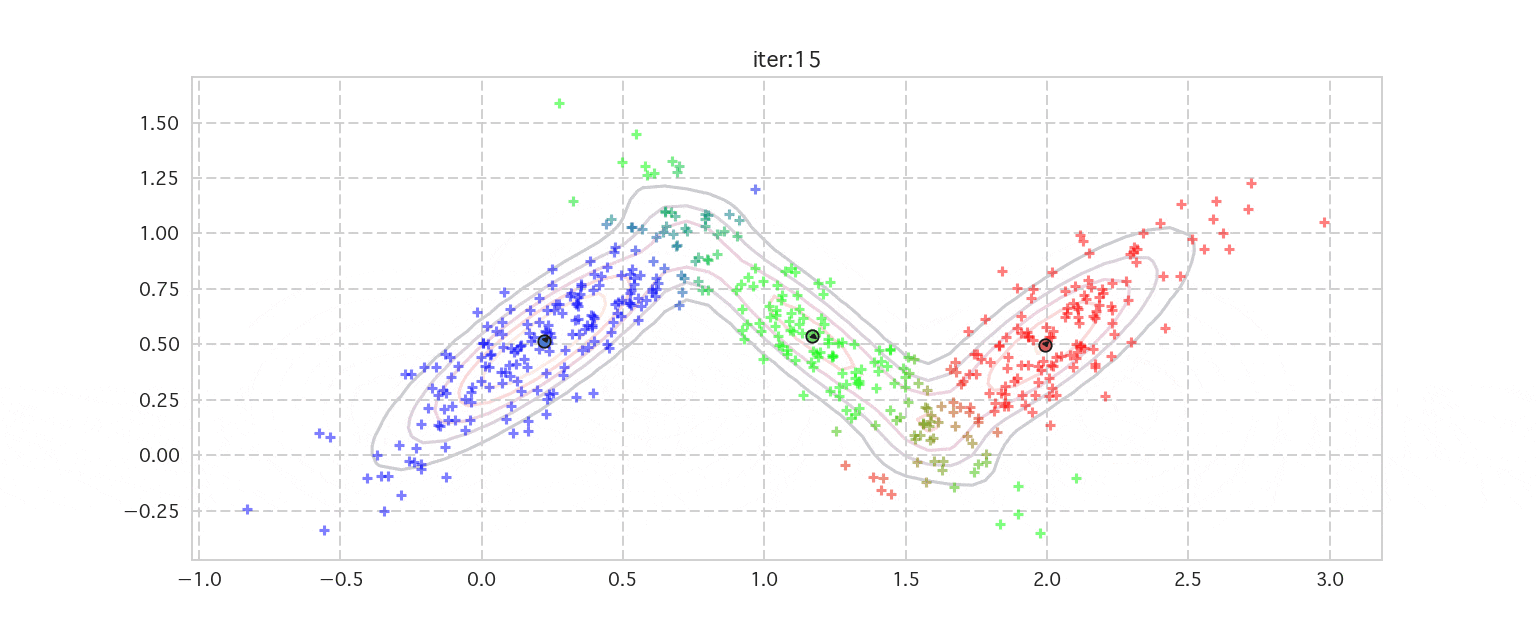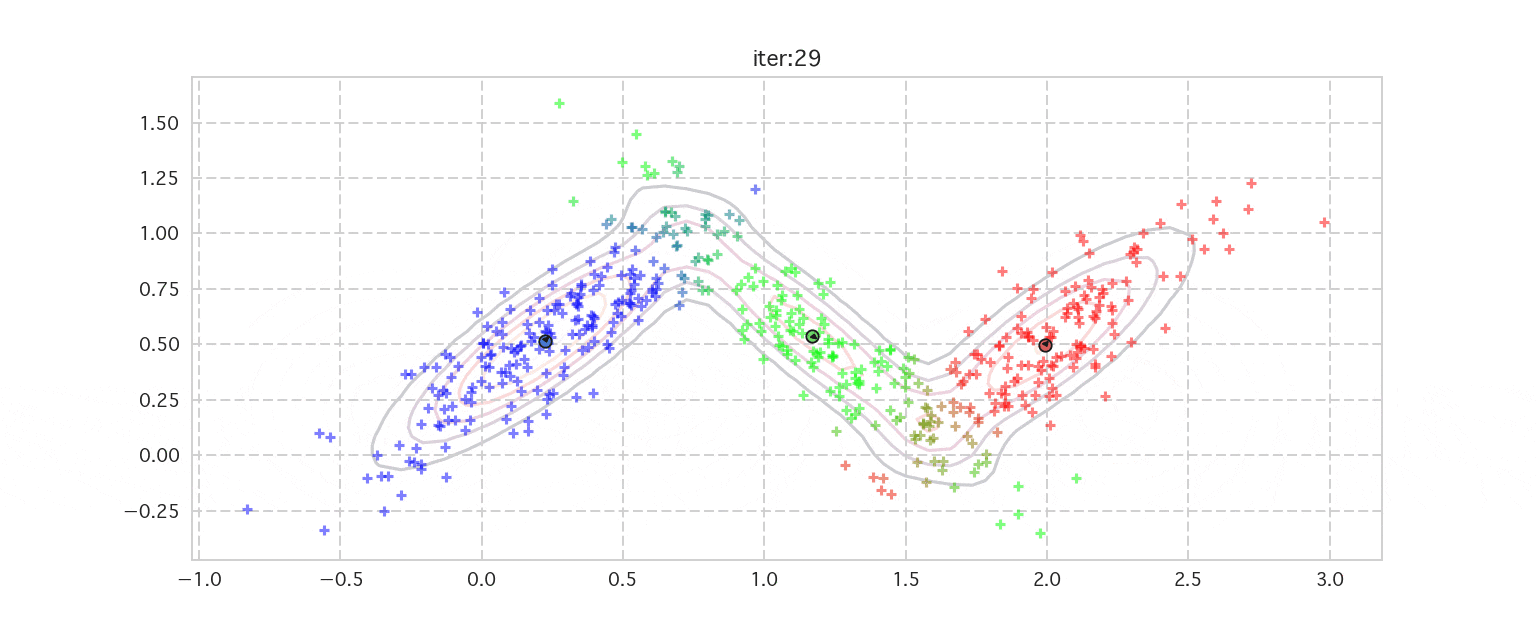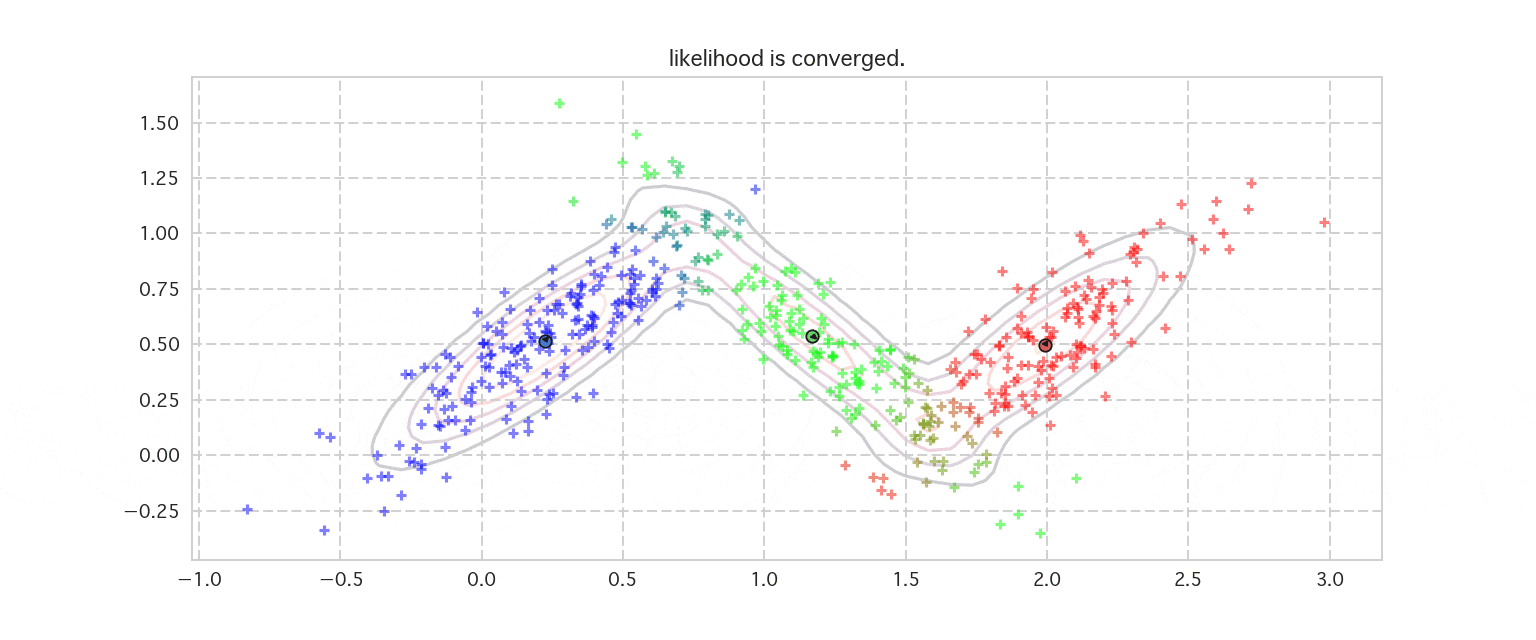
ここで使用する記号について、今回も記載します。

$x$ : $D$次元の確率変数
$z$ : $k$次元の確率変数であり、モデルの潜在変数
$\mathcal{D}=｛x_1,\cdots, x_N｝$ : $N$個の観測点（データ集合）
$K$ : クラスタの数（既知の定数）

まず、混合ガウス分布の確率密度関数を見てみましょう。

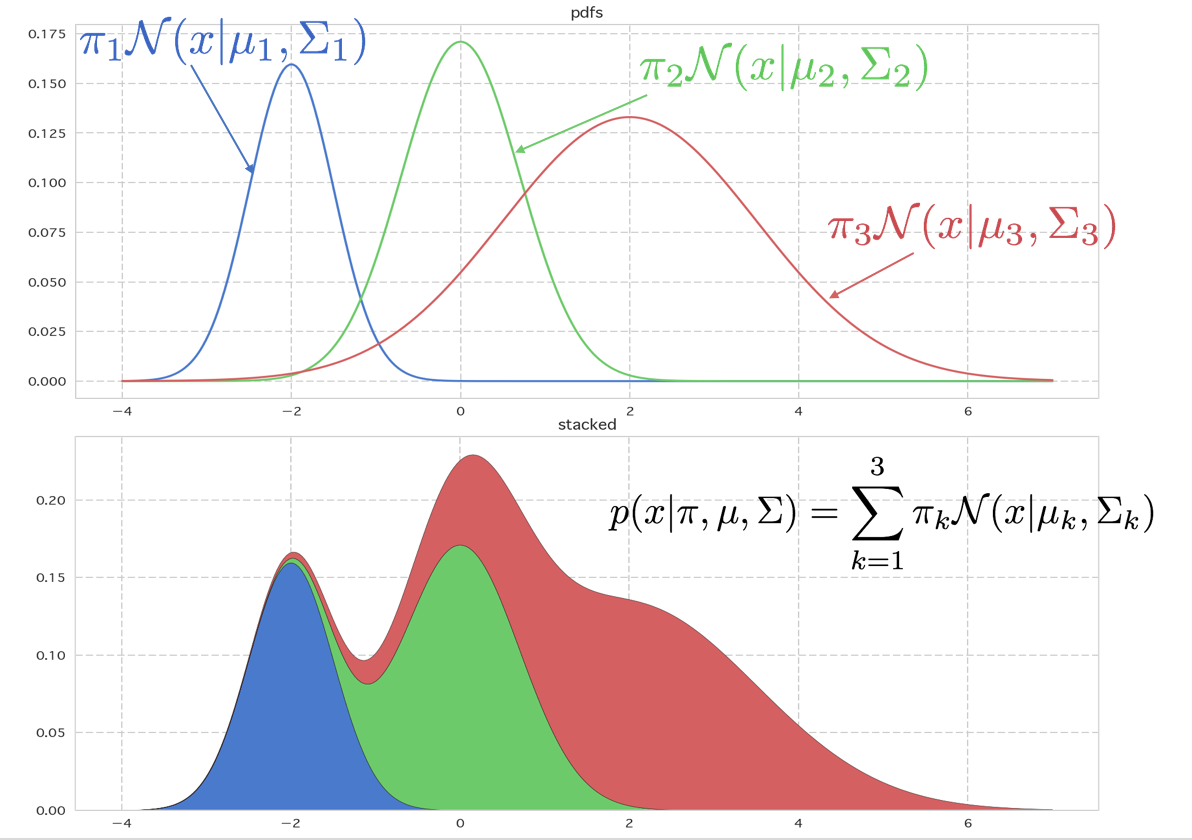
これは$K$個のガウス分布に比率をかけてたし合わせたものと見ることができます。下記に１次元の例を表示してみました。上の図は1つ1つのガウス分布が混合係数に従った比率$\pi_k$となった密度関数です。積分するとそれぞれ面積が$\pi_k$になります。
これを縦に積んだグラフが下のものです。これが混合ガウス分布の密度関数になります。$\sum_k \pi_k = 1$となるように$\pi_k$をとることとすると、面積がきちんと１になります。

GMMグラフ描画

# ======================================
# Parameters
K = 3
n = 301
xx = np.linspace(-4, 7, n)

mu = [-2, 0, 2]
sigma = [0.5, 0.7, 1.5]
pi = [0.2, 0.3, 0.5]

# Density function
pdfs = np.zeros((n, K))
for k in range(K):
    pdfs[:, k] = pi[k]*st.norm.pdf(xx, loc=mu[k], scale=sigma[k])
    
# =======================================
# Visualization
plt.figure(figsize=(14, 6))
for k in range(K):
    plt.plot(xx, pdfs[:, k])
plt.title("pdfs")
plt.show()

plt.figure(figsize=(14, 6))
plt.stackplot(xx, pdfs[:, 0], pdfs[:, 1], pdfs[:, 2])
plt.title("stacked")
plt.show()

3-2. 周辺尤度(エビデンス)による潜在変数の導入

データを生み出す確率分布がp(x)で表現されるとするとそこに周辺化や乗法定理を適用することで、潜在変数$z$を潜り込ませることができます。$\theta$はモデルのパラメーターです。

この$p(z)$とp(x|z)$が混合分布モデルにおいてどのようなものであるかを見ていきます。

さてまず、$p(z)$の分布を見ていきます。$z_{k}$ はk-meansの$r_{nk}$と同様どれかひとつの$k$について1をとる変数で、今回 $z_{k}$ は確率変数である点が違いです。やはり$z_{k}$は$z_{k}\in｛0, 1｝$かつ$\sum_k z_{k}=1$を満たします。
まず、潜在変数$\boldsymbol{z}=(z_{1},\cdots, z_{k},\cdots,z_{K})$の$k$番目の項 $z_{k}$ に注目します。$z_k$が$1$である確率は混合係数$\pi_k$によって決まり、

p(z_k=1) = \pi_k

です。パラメータ$\pi_k$は確率として考えるため、$0 \leq \pi_k \leq 1$、$\sum_{k=1}^K \pi_k = 1$を満たすこととします。
$z$でまとめて書くと

p(\boldsymbol{z}) = \prod_{k=1}^K \pi_k^{z_k}

のようにもかけます。
また、$z$ が与えられた元でのデータ$\boldsymbol{x}$の条件付き分布は、その条件が$z_k=1$であれば $k$番目のガウス分布に従うため、

p(\boldsymbol{x}|z_k = 1) = \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu_k}, \Sigma_k)

となる。これは条件を$\boldsymbol{z}$でかくと、

p(\boldsymbol{x}|\boldsymbol{z}) = \prod_{k=1}^K \mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu_k}, \Sigma_k) ^{z_k}

これら$p(z), p(x|z)$を(*1)に代入すると先ほど見た混合ガウス分布の密度関数と一致することがわかります。

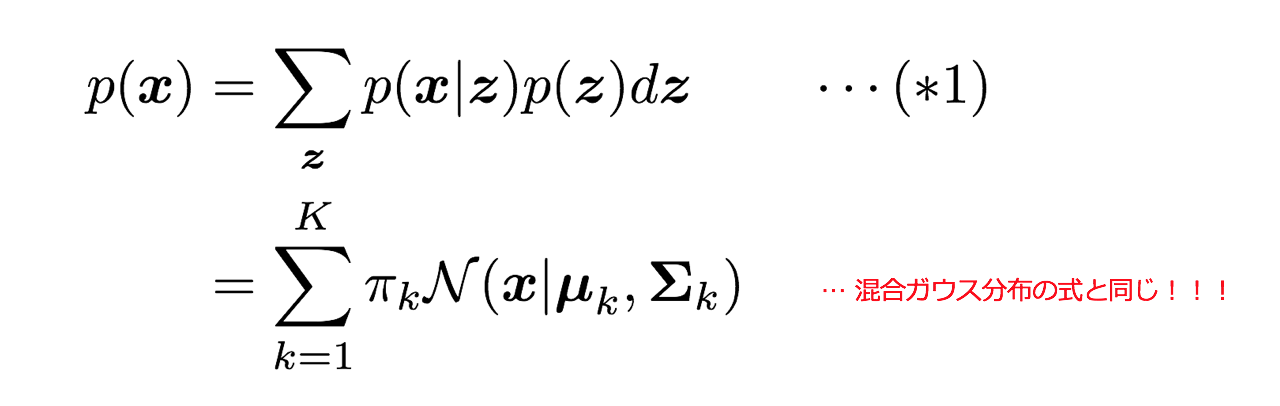
3−3. 負担率

先ほど見てきた$p(z)$と$(x|z)$よりベイズの定理を利用して$z$の事後分布を算出することができます。つまり、観測されたデータ$\boldsymbol{x}$から$z$の分布を見直すことができるということです。

この事後分布$p(z_k=1|\boldsymbol{x})$を$\gamma(z_k)$とおき、これを負担率と表現することがあります。この負担率を図解してみましょう。これを見てみると一目瞭然ですが、負担率とは、ある地点$\boldsymbol{x}$における混合ガウス分布の密度関数の値の中で、各$k$の分布が占める割合となっているのです。

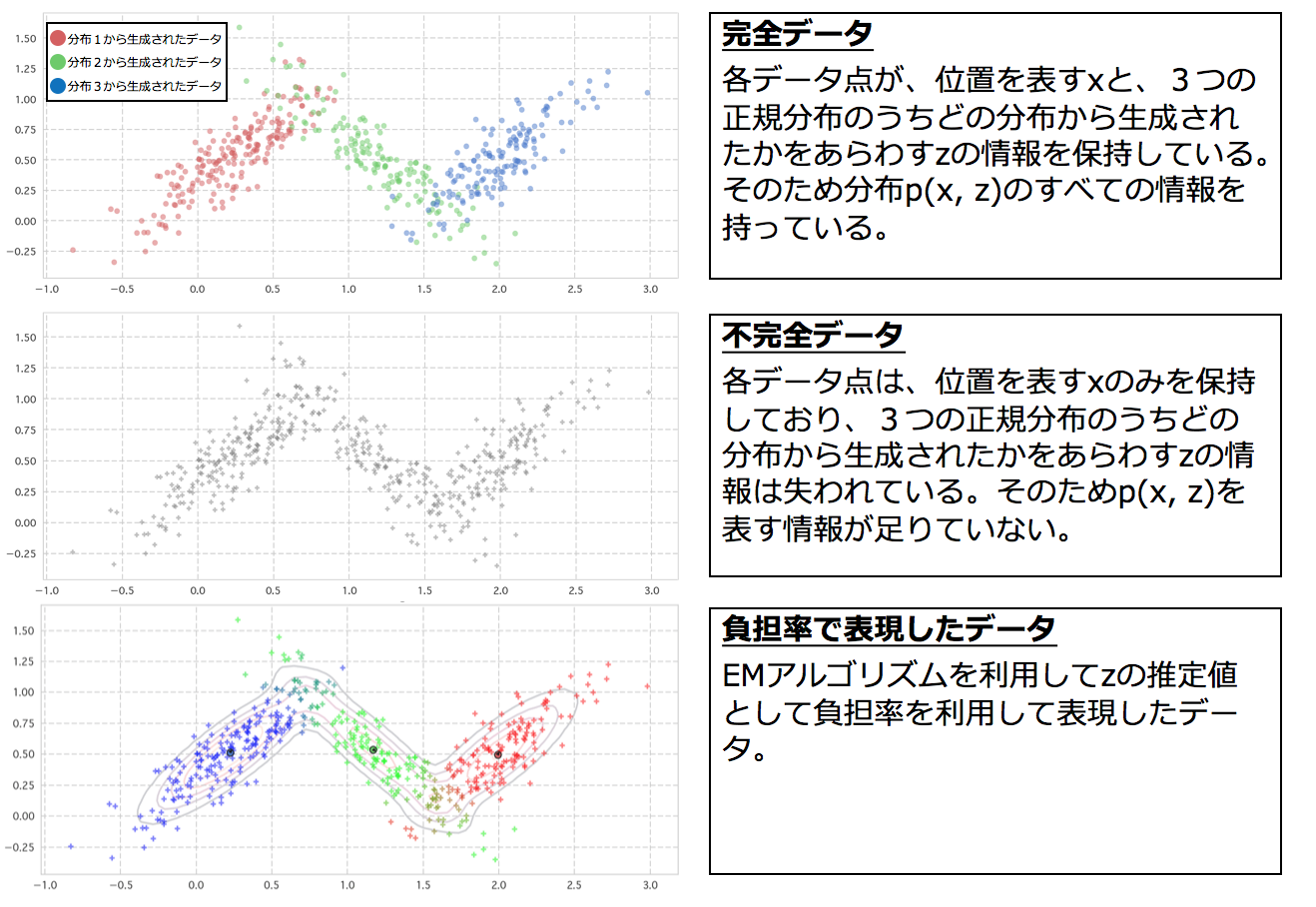
3−4. 完全データ集合集合と不完全データ集合

同時分布$p(x, z)$からのサンプルについて、その変数部分である$x, z$についての情報がデータとして残っているか否かで、データセットの種類を完全データ集合と不完全データ集合に分けることができる。のちにEMアルゴリズムの適用条件として完全データの対数尤度関数の最適化が可能であることがあるためここで一度取り上げます。

3−5. 最尤法の復習

さて、$z$ の分布とパラメーター$\theta$を推定するのがEMアルゴリズムですが、このEMアルゴリズムの説明をする前にまず最尤法について復習したいと思います。
$\theta$ でパラメトライズされた確率分布 $p(x|\theta)$ に従って生成された $N$ 個のデータ $\mathcal{D}=｛x_1,\cdots, x_N｝$を持っている時に、このデータを生み出すと考えられる最も良い$\theta$を探す方法を最尤法と言います。$x$は既に実現値なので定数として扱い、$\theta$を変数とし扱う確率を尤度と言い、$p(x|\theta)$を尤度関数と言います。（尤度についての丁寧な解説はコチラも参考）最も尤度の大きい、尤もらしい$\theta$を探すという手法のため、「最尤法」と言います。

**図2：データを生成する分布$p(x|\theta)$と、そこから生成された$N$個のデータ**

単純に良い$\theta$を探すだけではうまく潜在変数を扱うことができないケースにおいてEMアルゴリズムを適用すると、パラメーターと潜在変数がうまく推定できることがあり、これが今回のテーマです。

3−6. 混合ガウス分布へのEMアルゴリズム適用

まず改めて記号について記載します。

N個のデータを観測したときの混合ガウス分布の対数尤度関数は

であり、これを対象として尤度最大化を行っていきます。しかし、この対数尤度関数にはlog-sum部分があり解析的に解くことが難しいのです。そのための解法としてEMアルゴリズムを適用します。(log-sumの解消については後述)
まず先に方針を示したいと思います。

方針

[初期化] まず、求めるパラメータ$\boldsymbol{\pi}, \boldsymbol{\mu},\boldsymbol{\Sigma}$に初期値をセットし、対数尤度の計算結果を算出。
[Eステップ] 負担率$\gamma(z_{nk})$を計算する。
[Mステップ] 対数尤度関数をパラメータ$\boldsymbol{\pi}, \boldsymbol{\mu},\boldsymbol{\Sigma}$で微分して０と置き、最尤解を求める。
[収束確認] 対数尤度を再計算し、前回との差分があらかじめ設定していた収束条件を満たしていなければ2.にもどる、満たしていれば終了する。

3.で負担率を求める理由は、4.で求める最尤解に負担率$\gamma(z_{nk})$が現れるためです。方針の1. 2. 4はすでに計算できる状態のため、3.の最尤解を求めていきたいと思います。

3-6-1. μの最尤解を求める

まず$\ln \mathcal{N}(x|\mu, \Sigma)$の$\mu$に関する微分を事前準備として求めておきます。

$\boldsymbol{\mu}_k$に関する最大値を探すので、これを０とおくと

$\boldsymbol{\mu}_k$の最尤解が求められた。

3-6-2. Σの最尤解を求める

$\Sigma$についても$\ln \mathcal{N}(x|\mu, \Sigma)$の$\Sigma$に関する微分を事前準備として求めておきます。

$\boldsymbol{\Sigma}_k$についての微分を対数尤度関数に対して行うと

微分して０とおくので

これで$\boldsymbol{\Sigma}_k$の最尤解が求められた。

3-6-3. πの最尤解を求める

最後に$\pi$の最尤解ですが、これは前の2つとは違い、

\sum_{k=1}^K \pi_k = 1

という制約条件が付いています。この場合制約条件付き最大化を行う手法としてラグランジュの未定乗数法を利用して解いていきます。
まずこの制約条件の式を右辺を0にしたもの

\sum_{k=1}^K \pi_k - 1 = 0

を作りこれにラグランジュの未定乗数$\lambda$を掛け、元々の最大化の目的の項に足してあげることで最適化対象の式を作ります。

G = L + \lambda\left(\sum_{k=1}^K \pi_k - 1  \right)

$L$は対数尤度です。

よって(*4)より

3−8. EMアルゴリズムによる混合ガウス分布の推定

EMアルゴリズムによる混合ガウス分布の推定
1.　[初期化] まず、求めるパラメータ$\boldsymbol{\pi}, \boldsymbol{\mu},\boldsymbol{\Sigma}$に初期値をセットし、対数尤度の計算結果を算出。
2.　[Eステップ] 負担率$\gamma(z_{nk})$を計算する。

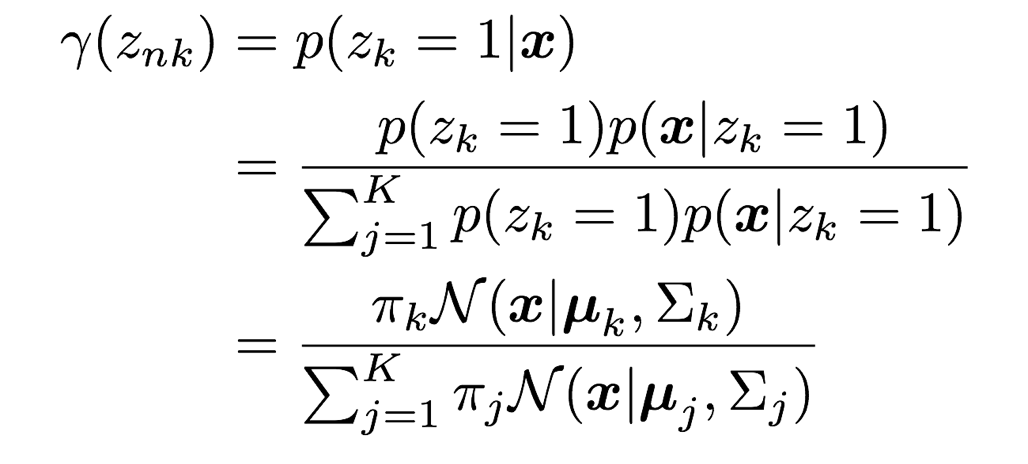
3.　[Mステップ] 対数尤度関数をパラメータ$\boldsymbol{\pi}, \boldsymbol{\mu},\boldsymbol{\Sigma}$で微分して０と置き、最尤解を求める。

4.　[収束確認] 対数尤度を再計算し、前回との差分があらかじめ設定していた収束条件を満たしていなければ2.にもどる、満たしていれば終了する。

3−7. EMアルゴリズムによる混合ガウス分布の推定の実装

GMMに対するEMアルゴリズム

for nframe in range(100):
    global mu, sigma, pi
    print('nframe:', nframe)
    plt.clf()
    
    if nframe <= 3:
        print('initial state')
        plt.scatter(data[:,0], data[:,1], s=30, c='gray', alpha=0.5, marker="+")
        for i in range(3):
            plt.scatter([mu[i, 0]], [mu[i, 1]], c=c[i], marker='o', edgecolors='k', linewidths=1)
        print_gmm_contour(mu, sigma, pi, K)
        plt.title('initial state')
        return

    # E step ========================================================================
    # calculate responsibility(負担率)
    likelihood = calc_likelihood(data, mu, sigma, pi, K)
    gamma = (likelihood.T/np.sum(likelihood, axis=1)).T
    N_k = [np.sum(gamma[:,k]) for k in range(K)]

    # M step ========================================================================

    # caluculate pi
    pi =  N_k/N

    # calculate mu
    tmp_mu = np.zeros((K, D))

    for k in range(K):
        for i in range(len(data)):
            tmp_mu[k] += gamma[i, k]*data[i]
        tmp_mu[k] = tmp_mu[k]/N_k[k]
    mu_prev = mu.copy()
    mu = tmp_mu.copy()

    # calculate sigma
    tmp_sigma = np.zeros((K, D, D))

    for k in range(K):
        tmp_sigma[k] = np.zeros((D, D))
        for i in range(N):
            tmp = np.asanyarray(data[i]-mu[k])[:,np.newaxis]
            tmp_sigma[k] += gamma[i, k]*np.dot(tmp, tmp.T)
        tmp_sigma[k] = tmp_sigma[k]/N_k[k]

    sigma = tmp_sigma.copy()

    # calculate likelihood
    prev_likelihood = likelihood
    likelihood = calc_likelihood(data, mu, sigma, pi, K)
    
    prev_sum_log_likelihood = np.sum(np.log(prev_likelihood))
    sum_log_likelihood = np.sum(np.log(likelihood))
    diff = prev_sum_log_likelihood - sum_log_likelihood
    
    print('sum of log likelihood:', sum_log_likelihood)
    print('diff:', diff)

    print('pi:', pi)
    print('mu:', mu)
    print('sigma:', sigma)

    # visualize
    for i in range(N):
        plt.scatter(data[i,0], data[i,1], s=30, c=gamma[i], alpha=0.5, marker="+")

    for i in range(K):
        ax = plt.axes()
        ax.arrow(mu_prev[i, 0], mu_prev[i, 1], mu[i, 0]-mu_prev[i, 0], mu[i, 1]-mu_prev[i, 1],
                  lw=0.8, head_width=0.02, head_length=0.02, fc='k', ec='k')
        plt.scatter([mu_prev[i, 0]], [mu_prev[i, 1]], c=c[i], marker='o', alpha=0.8)
        plt.scatter([mu[i, 0]], [mu[i, 1]], c=c[i], marker='o', edgecolors='k', linewidths=1)
    plt.title("step:{}".format(nframe))
    
    print_gmm_contour(mu, sigma, pi, K)
    
    if np.abs(diff) < 0.0001:
        plt.title('likelihood is converged.')
    else:
        plt.title("iter:{}".format(nframe-3))

4.一般のEMアルゴリズム

4−1. 対数尤度の分解

ここまではデータが混合ガウス分布に従っているとして話を進めてきましたが、特定の分布を仮定しないEMアルゴリズムを見ていきたいと思います。

記号

$\boldsymbol{X}$ : 観測変数
$\boldsymbol{Z}$ : 潜在変数
$\theta$ : 分布のパラメーター

$\ln p(\boldsymbol{X}|\theta)$を最大化したいのですが、基本的に$\ln p(\boldsymbol{X}|\theta)$を直接最適化することは難しいことが知られています。不完全データである$p(\boldsymbol{X}|\theta)$の対数尤度関数は難しいのですが、完全データの尤度関数$\ln p(\boldsymbol{X}, \boldsymbol{Z}|\theta)$が最適化可能であればEMアルゴリズムの適用が可能です。よってまずは周辺化により潜在変数を導入し完全データの分布型で表現できるようにします。(この太字で表した仮定が後で重要になります)

完全データの分布で表現できたのはいいのですが、これに対数をかけてみると、左辺にlog-sumが出てきてしまい、解析的に取り扱うことが困難です。

よってまずは$\ln p(\boldsymbol{X}|\theta)$を変形して、最適化可能な変分下限というものを導出します。

イェンセンの不等式により、log-sumをsum-logの形で書き換えることができました！参考：イェンセン(Jensen)の不等式の直感的理解： http://qiita.com/kenmatsu4/items/26d098a4048f84bf85fb

$\mathcal{L}(q, \theta)$の$q$は変数ではなく関数なので、$\mathcal{L}(q, \theta)$は$q(\boldsymbol{Z})$の汎関数です。（汎関数についてはPRMLの付録Dを参照してください）

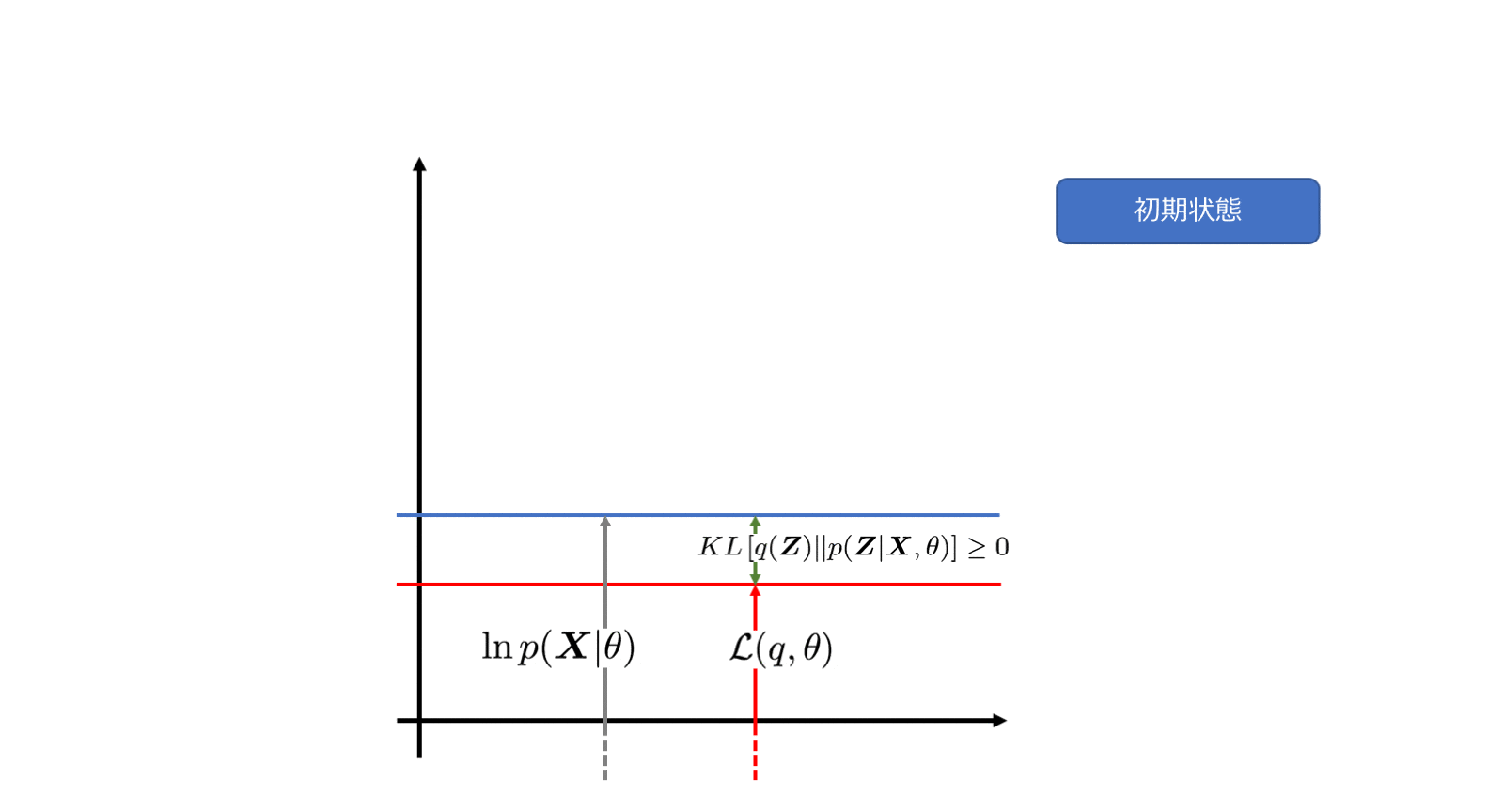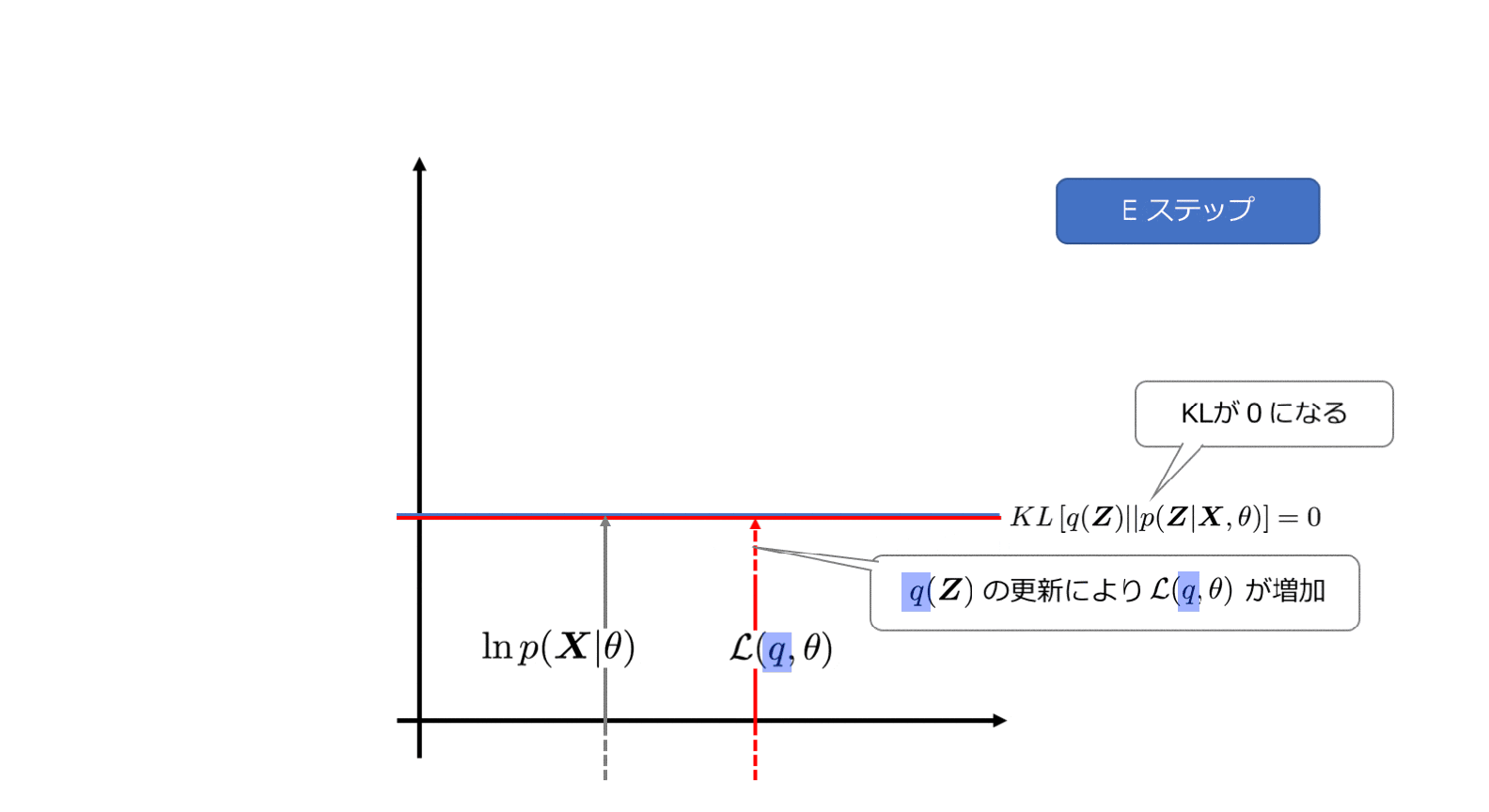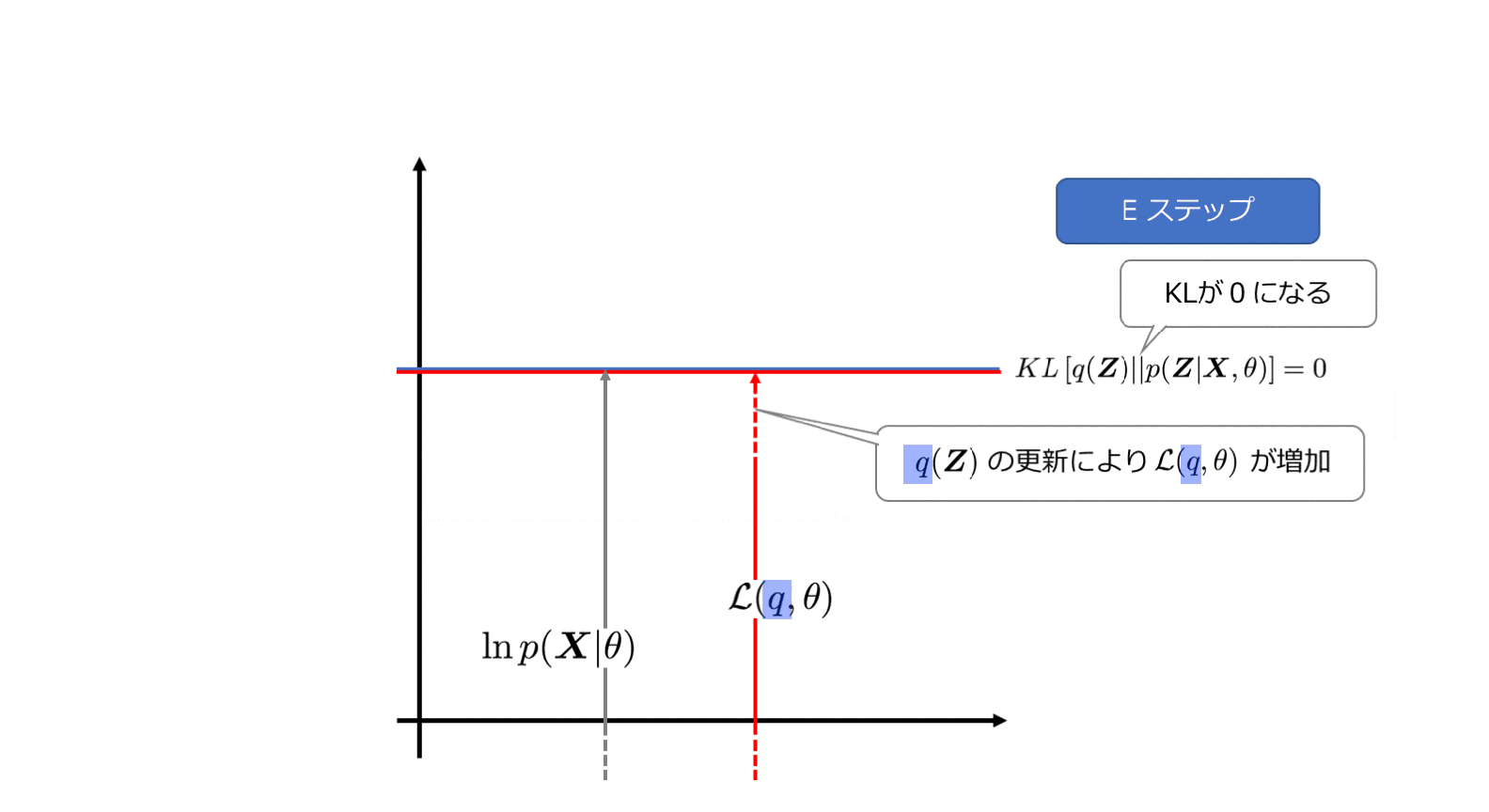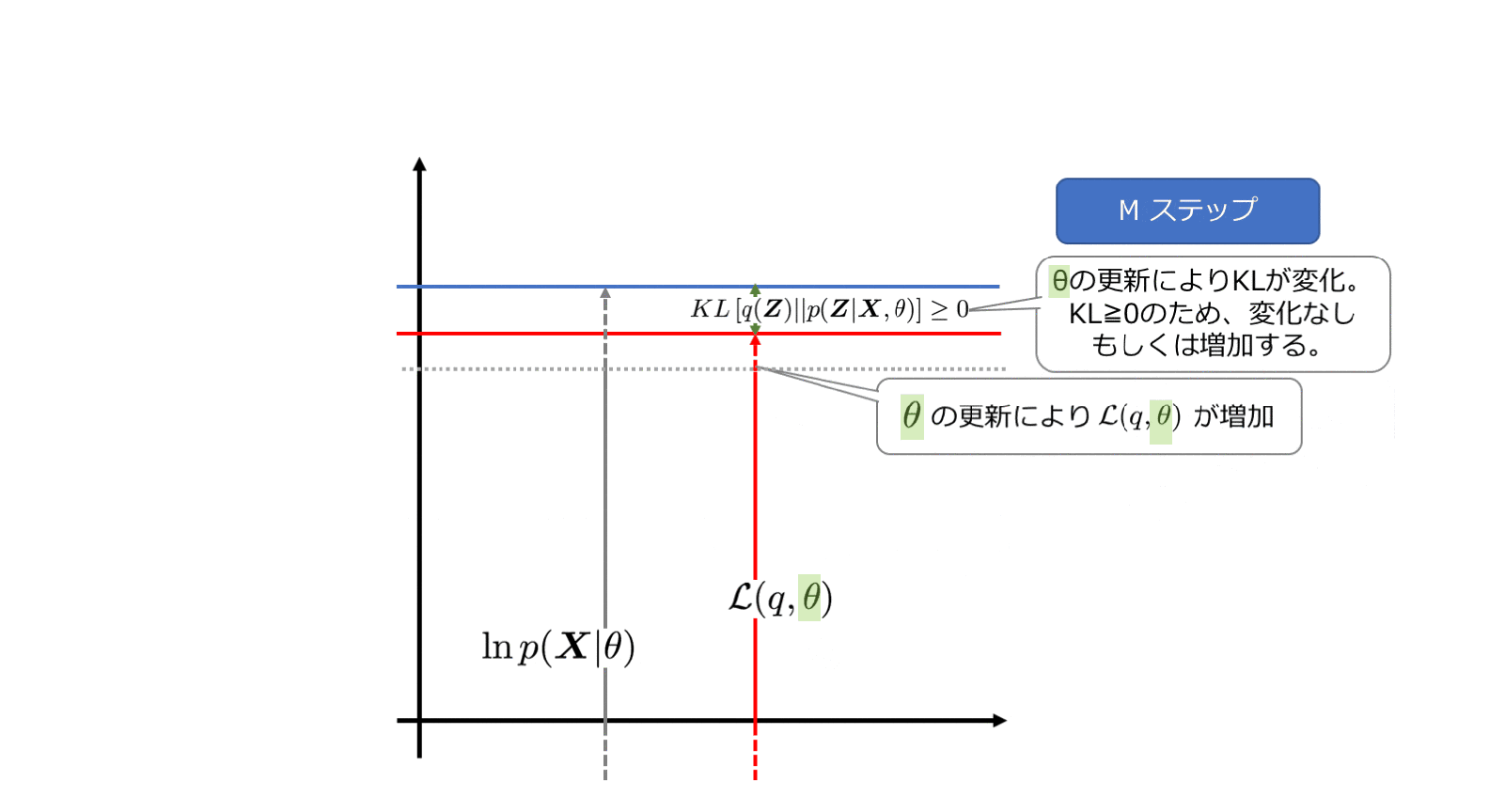
$\ln p(\boldsymbol{X}|\theta) \geq \mathcal{L}(q, \theta)$ということは、その間には何が入るのでしょうか？ここには$KL\left[q(\boldsymbol{Z}) || p(\boldsymbol{Z}|\boldsymbol{X}, \theta) \right] $というカルバックライブラーダイバージェンスと呼ばれる$\boldsymbol{Z}$の分布$q(\boldsymbol{Z})$と、その事後分布$p(\boldsymbol{Z}|\boldsymbol{X}, \theta)$がどれくらい近いかを表すものがはいります。

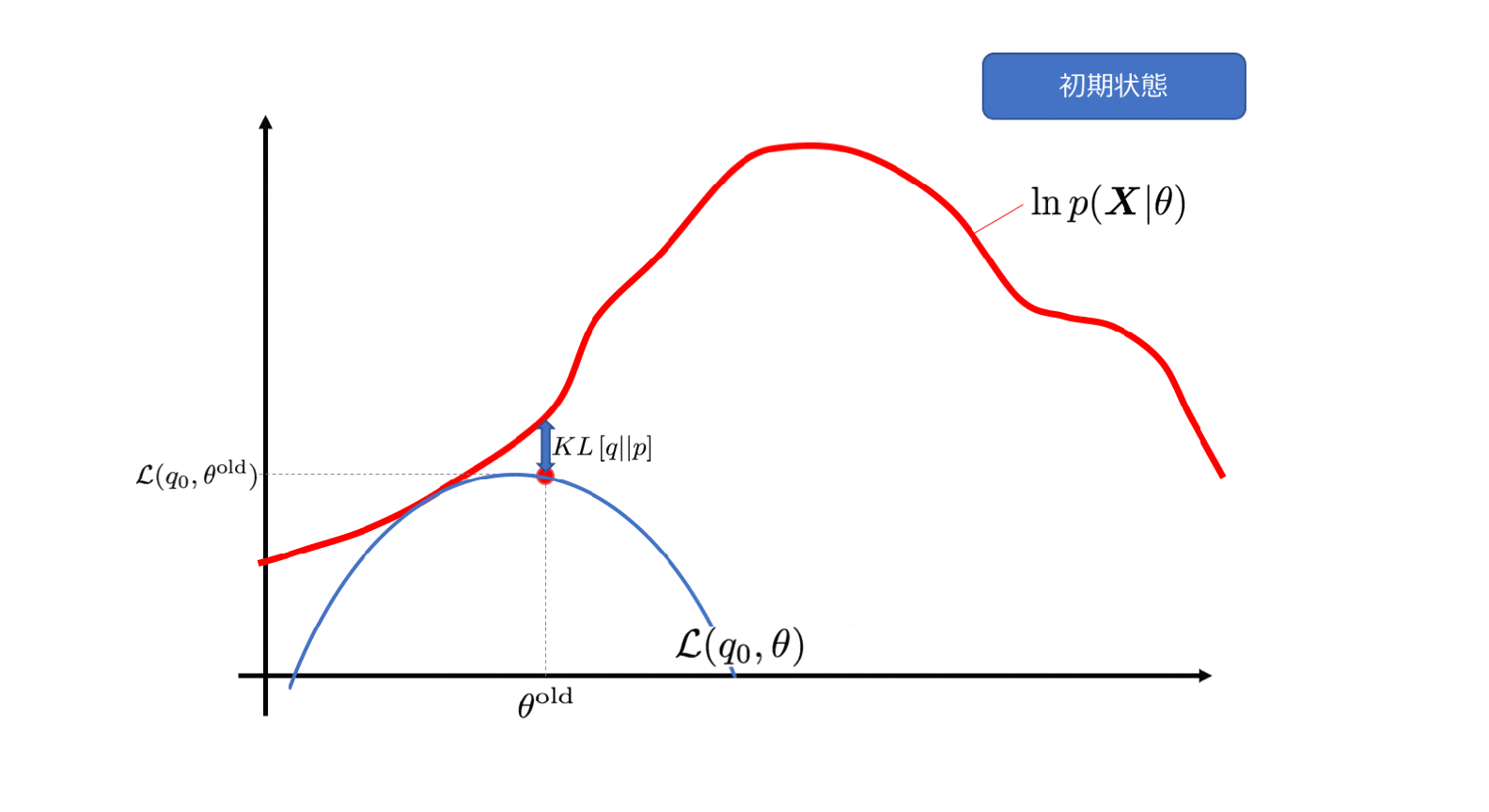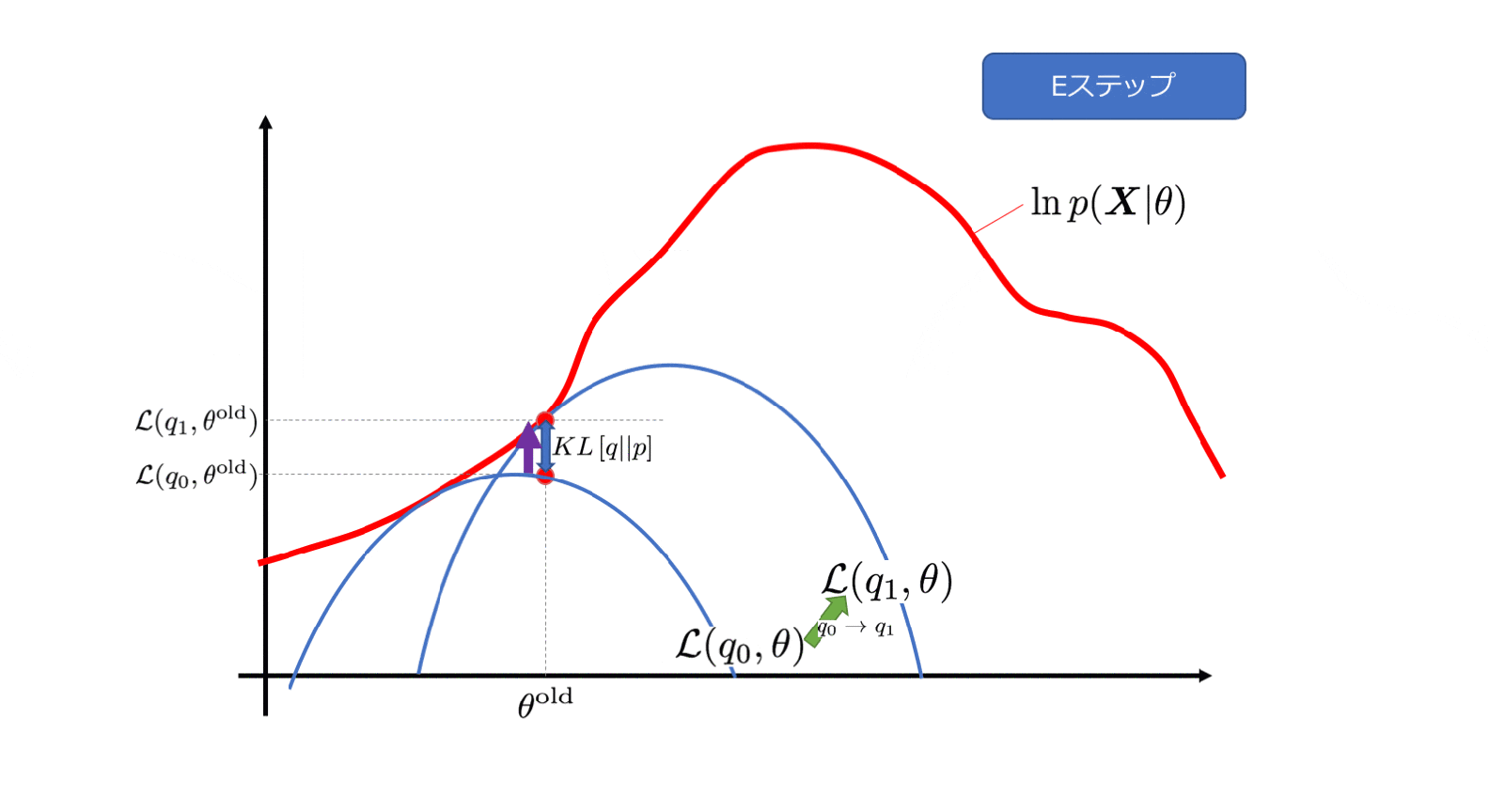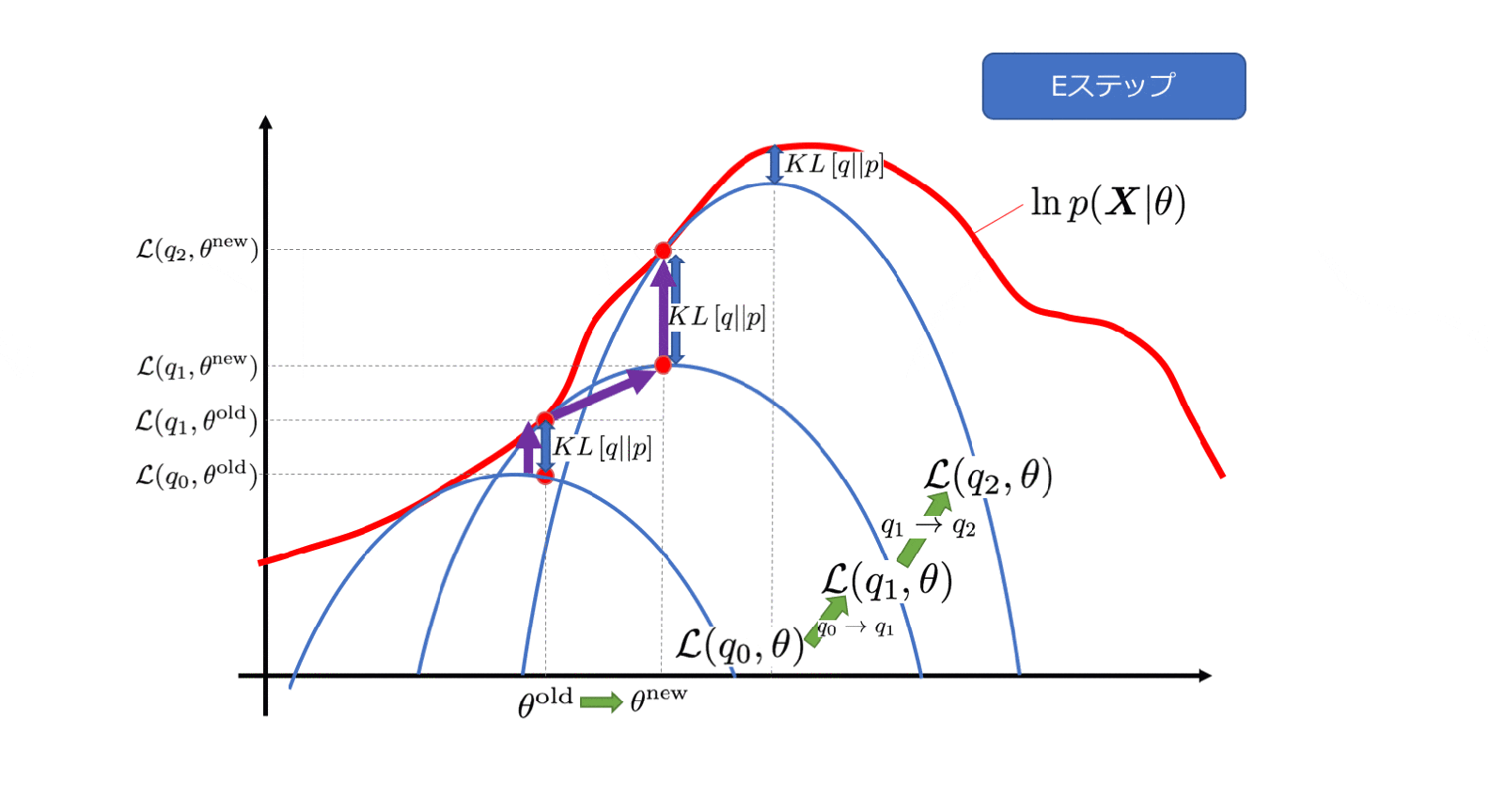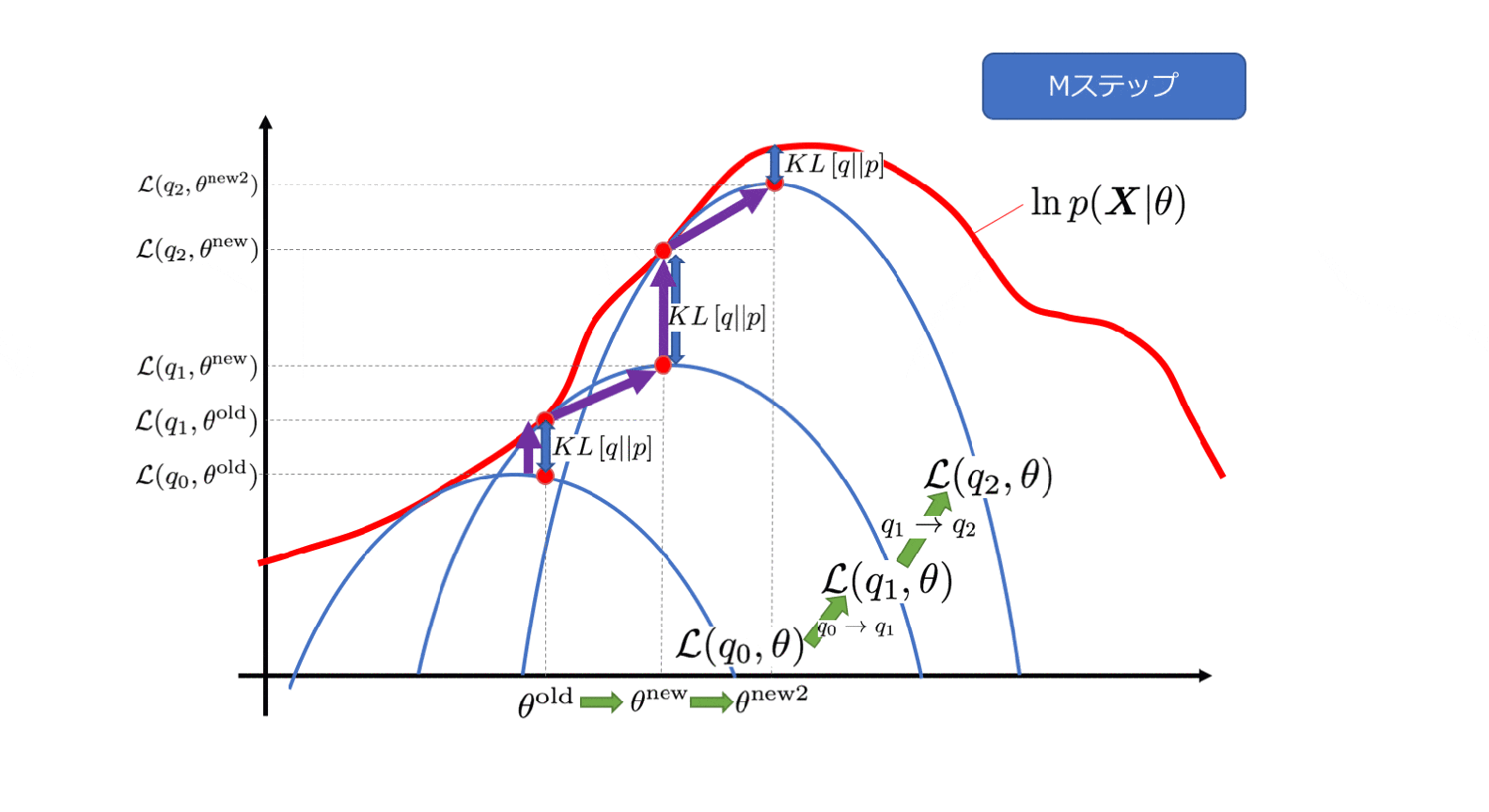
カルバックライブラーダイバージェンス$KL\left[q(\boldsymbol{Z}) || p(\boldsymbol{Z}|\boldsymbol{X}, \theta) \right] $は$KL\geq0$となることが知られています。そのため各項の関係は下記の図のようになります。

4−2. EMアルゴリズムの概略

変分下限$\mathcal{L}(q, \theta)$の引数$q$と$\theta$をそれぞれ交互に最適化することで、本当のターゲットである$\ln p(\boldsymbol{X|\theta})$の最大化を図ります。

先ほど仮定を置いていた「**完全データの尤度関数**$\ln p(\boldsymbol{X},\boldsymbol{Z}|\theta)$**が最適化可能であれば**」がここで役に立ちます。 Mステップはこの仮定により最適化が可能なのです。アニメーションで表現すると下記の通りです。

さて下記でEステップと、Mステップそれぞれの詳細を見ていきます。

4−3. Eステップ

Eステップでは、$\ln p(\boldsymbol{X|\theta})$を最大にするような$q$を選びます。この時、$\theta$は固定値とみなします。

KLが0になるので、このとき

\ln p(\boldsymbol{X}|\theta)=\mathcal{L}(q, \theta)

のように、変分下限は対数尤度に等しくなります。先ほどのアニメーションでもグレーの矢印と赤い矢印の長さが同じになっていましたね。

4−4. Mステップ

Mステップでは$q(\boldsymbol{Z})$を固定して$\theta$を最大化します。その際、事後分布の算出に利用していた$\theta$は$\theta^{{\rm old}}$としてその値をキープして数値計算を行います。

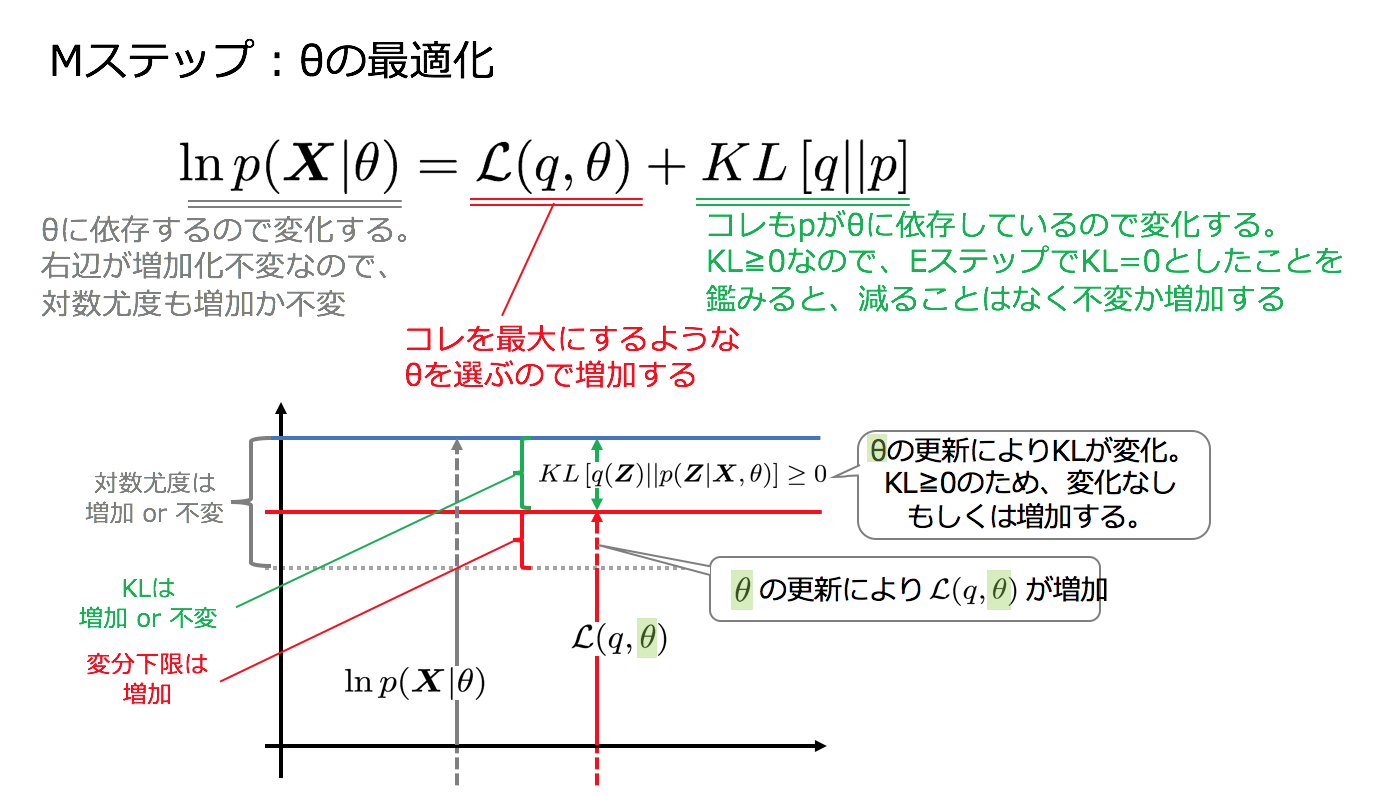
ということで、完全データの対数尤度を最適か可能と前提をおいていたので、$\mathcal{L}(q, \theta)$は最適化することができるようになりました。

4−5. パラメータ空間におけるEMアルゴリズムの表現

横軸をパラメータ$\theta$と置いたときのEMアルゴリズムのイテレーションをアニメーションで表現してみました。Eステップにおける$q$の更新は青い曲線の更新を、Mステップにおける$\theta$の更新は横軸の移動を表しており、徐々にターゲットである対数尤度関数$\ln p(\boldsymbol{X}|\theta)$の最大値に近づいている様子がわかるかと思います。

4−6. 一般のEMアルゴリズムのまとめ

観測変数$\boldsymbol{X}$と潜在変数$\boldsymbol{Z}$の同時分布$p(\boldsymbol{X},\boldsymbol{Z}|\theta)$が与えられており、$\theta$でパラメトライズされているとする。対数尤度関数$\ln p(\boldsymbol{X}|\theta)$の$\theta$nについての最大化は下記のステップにより実現できる。

1.　パラメータの初期化
　$\theta^{{\rm old}}$を初期化する。

2.　Eステップ
　$\boldsymbol{Z}$ の事後分布 $p(\boldsymbol{Z}| \boldsymbol{X}, \theta)$を計算する。

3.　Mステップ
　事後分布 $p(\boldsymbol{Z}| \boldsymbol{X}, \theta)$による対数尤度の期待値

\mathcal{Q}(\theta, \theta^{{\rm old}}) = \sum_{\boldsymbol{Z}} q(\boldsymbol{Z}|\boldsymbol{X}, \theta^{{\rm old}}) \ln p(\boldsymbol{X}, \boldsymbol{Z}|\theta)

　を計算し、$\theta$の更新を行う。

\theta^{{\rm new}} = \arg \max_{\theta} \mathcal{Q}(\theta, \theta^{{\rm old}} )

4.　対数尤度関数$\ln p(\boldsymbol{X}, \boldsymbol{Z}|\theta)$を計算し、収束条件を満たしているか確認。
　満たされている場合：　終了する
　満たされていない場合：　$\theta^{{\rm old}} \leftarrow \theta^{{\rm new}}$で$\theta$を更新し、ステップ2に戻る。

5.混合ガウス分布推定の解釈

さて、具体例として取り上げていた混合ガウス分布に戻り、先ほどの一般のEMアルゴリズムとの対応を見ていきたいと思います。そのための道具としてまず下記の5つを見ていきます。

$p(\boldsymbol{Z})$ ： $\boldsymbol{Z}$の事前分布
$p(\boldsymbol{X}|\boldsymbol{Z})$ ： $\boldsymbol{X}$の$\boldsymbol{Z}$での条件付き分布
$\ln p(\boldsymbol{X},\boldsymbol{Z}|\boldsymbol{\pi},\boldsymbol{\mu},\boldsymbol{\Sigma})$ ：完全データの対数尤度関数
$\ln p(\boldsymbol{Z}|\boldsymbol{X},\boldsymbol{\pi},\boldsymbol{\mu},\boldsymbol{\Sigma})$ ： $\boldsymbol{Z}$の事後分布
$\mathbb{E}_{\boldsymbol{Z}|\boldsymbol{X}}[\ln p(\boldsymbol{X},\boldsymbol{Z}|\boldsymbol{\pi},\boldsymbol{\mu},\boldsymbol{\Sigma})]$ ： Zの事後分布による完全データの対数尤度関数の期待値

$\boldsymbol{z}_n$を下記を満たす確率変数とします。

5-1. 最尤推定の準備

5-1-1. Zの事前分布

5-1-2. XのZでの条件付き分布

5-1-3. 完全データの対数尤度関数

5-1-4. Zの事後分布

5-1-5. Zの事後分布によるz_{nk}の期待値

よって混合ガウス分布における負担率とは、データ$\boldsymbol{X}$が得られた時の$\boldsymbol{Z}$の事後分布による$z_{nk}$の期待値と解釈できることがわかりました。

5-1-6. Zの事後分布による完全データの対数尤度関数の期待値

一般のEMアルゴリズム 4−4.Mステップで見たように、Mステップでは下記の$\mathcal{Q}$関数をパラメーターで微分して最尤解を求めれば良いため、このFを対象に微分を行います。

\mathcal{Q}(\theta, \theta^{{\rm old}}) = \sum_{\boldsymbol{Z}} q(\boldsymbol{Z}|\boldsymbol{X}, \theta^{{\rm old}}) \ln p(\boldsymbol{X}, \boldsymbol{Z}|\theta)