1. Pythonで学ぶ統計学 2. 確率分布[scipy.stats徹底理解]

• データから計算される確率分布のことを**「経験分布」**といいます。これに対して、**確率分布を生成してくれる関数は「理論分布」**といいます。
• まず、**分布の形（確率分布の種類）を決める、それから母数（確率分布のパラメータ）**を決めてしまえば、母集団分布の推定ができます。
• そうした統計関数を集めたモジュールがscipy.statsです。その基本的な使い方は、次のように記法が統一されています。

#⑴ 確率分布の種類

• 確率関数は**「離散型」と「連続型」**の２つに大別されます。
• 離散型は、例えばサイコロの目のようにとびとびの値をとる変数です。また連続型は、重量や温度のように連続した値をとるものをいいます。
• 以下に、scipy.statsに実装されている確率分布から、知っておきたい15種類を列挙しました。

	確率分布	probability distribution	メソッド	データ
1	超幾何分布	Hypergeometric distribution	scipy.stats.hypergeom	離散型
2	ベルヌーイ分布	Bernoulli distribution	scipy.stats.bernoulli	離散型
3	二項分布	binomial distribution	scipy.stats.binom	離散型
4	ポアソン分布	Poisson distribution	scipy.stats.poisson	離散型
5	幾何分布	Geometric Distribution	scipy.stats.geom	離散型
6	負の二項分布	Negative Binomial Distribution	scipy.stats.nbinom	離散型
7	一様分布	uniform distribution	scipy.stats.uniform	離散型
8	正規分布	normal distribution	scipy.stats.norm	連続型
9	指数分布	exponential distribution	scipy.stats.expon	連続型
10	ガンマ分布	gamma distribution	scipy.stats.gamma	連続型
11	ベータ分布	beta distribution	scipy.stats.betabinom	連続型
12	コーシー分布	Cauchy distribution	scipy.stats.cauchy	連続型
13	対数正規分布	lognormal distribution	scipy.stats.lognorm	連続型
14	パレート分布	Pareto distribution	scipy.stats.pareto	連続型
15	ワイブル分布	Weibull distribution	scipy.stats.dweibull	連続型

• これらの確率分布は、ほぼ共通のメソッドを実装しています。
• 従って、メソッドを理解すれば、いろいろな確率分布を操作することが可能となります。

#⑵ 各種メソッドの機能

• ここでは、もっとも使用頻度が高い**正規分布scipy.stats.norm**を例として、主要なメソッドを見ていきます。
• 引数となるのは、入力データx、パラメータである**期待値（平均値）locと標準偏差scale**のほか、要素の数size、**乱数生成のシードrandom_state=整数**などです。

# 数値計算のためのライブラリ
import numpy as np
from scipy import stats

# グラフ描画のためのライブラリ
import matplotlib.pyplot as plt
%matplotlib inline

# matplotlibを日本語表示に対応させるモジュール
!pip install japanize-matplotlib
import japanize_matplotlib

##➀ rvs (Random variates) 確率変数

• 記法：rvs(loc=0, scale=1, size=1, random_state=None)
• 確率変数は、確率的な法則に従って変化する値のことです。
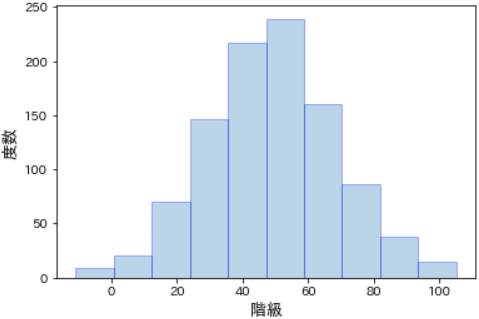
• 指定したパラメータに基づいて、**正規分布に従う確率変数（取り得る値）**を、ランダムに指定した個数だけ生成します。

# rvsで正規分布に従う疑似乱数を生成
norm_rvs = stats.norm.rvs(loc=50, scale=20, size=1000, random_state=0) # 期待値=50, 標準偏差=20, 個数=1000

# 可視化（ヒストグラムに表現）
plt.hist(norm_rvs, bins=10, alpha=0.3, ec='blue')
plt.xlabel("階級", fontsize=13)
plt.ylabel("度数", fontsize=13)

plt.show()

##➁ pdf (Probability density function) 確率密度関数

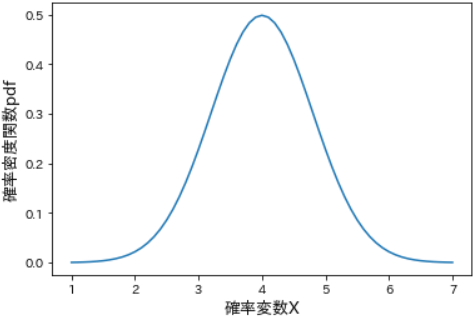
• 記法：pdf(x, loc=0, scale=1)
• 確率密度は、定義された域内での確率変数Xの値の相対的な出やすさを表します。
• 平たく言えば、確率密度関数は、連続型のデータを引数にとると確率密度が算出される関数のことです。

# 等差数列を生成
X = np.arange(start=1, stop=7.1, step=0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8 

# 可視化
plt.plot(X, norm_pdf)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度pdf", fontsize=13)
plt.show()

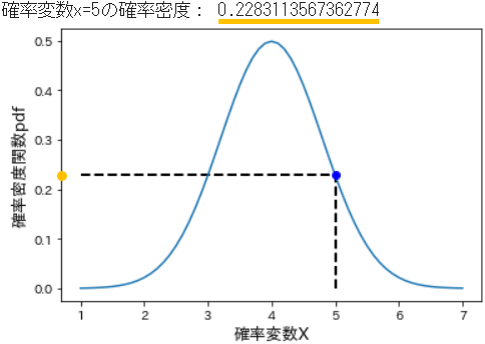
• 試みに、確率変数 x=5 のときの確率密度を確認してみます。

# 確率変数5のときの確率密度を計算
x = 5
y = stats.norm.pdf(x=x, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8
print("確率変数x=5のときの確率密度：", y)

# 確率密度関数のグラフにプロット
plt.plot(X, norm_pdf)
plt.plot(x, y, 'bo') # 青色ドットを布置

plt.vlines(x, 0.0, y, lw=2, linestyles='dashed') # 垂直線
plt.hlines(y, 1.0, x, lw=2, linestyles='dashed') # 水平線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度pdf", fontsize=13)

plt.show()

• 確率密度関数pdfは連続型データのためのメソッドであり、離散型データには次の確率質量関数pmfを使います。

##➂ pmf (Probability mass function) 確率質量関数

• 記法：pmf(k, n, p, loc=0)
• 確率質量は、確率変数Xのとびとびの要素ごとの相対的な出やすさを表します。
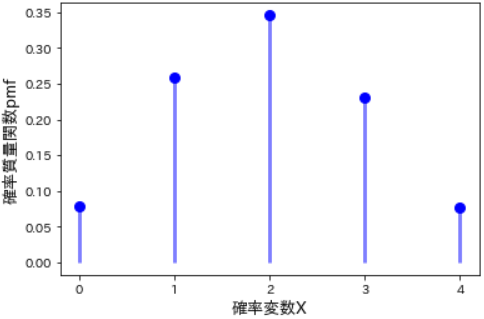
• 平たく言えば、確率質量関数は、離散型のデータを引数にとると確率質量が算出される関数のことです。
• ここでは２項分布を例として、「成功確率40％の試行を５回行ったとき、そのうち成功する回数（０～４回）ごとの確率」を示します。

# 成功確率
p = 0.4
# 試行回数
n = 5
# 成功回数
k = np.arange(0, 5) # array([0, 1, 2, 3, 4])

# pmfで成功回数ごとの確率を計算
binom_pmf = stats.binom.pmf(k, n, p) # 成功回数=0～4, 試行回数=5, 成功確率=0.4

# 可視化
plt.plot(k, binom_pmf, 'bo', ms=8)
plt.vlines(k, 0, binom_pmf, colors='b', lw=3, alpha=0.5)

plt.xticks(k) # x軸目盛

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率質量関数pmf", fontsize=13)

plt.show()

##➃ logpdf (Log of the probability density function) ログ確率密度関数

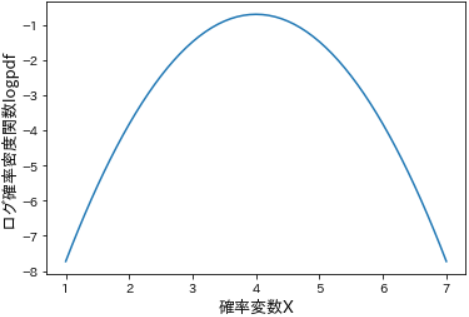
• 記法：logpdf(x, loc=0, scale=1)
• ログ確率密度関数は、底をeとする確率密度の対数をとったものです。
• ネイピア数 $e=2.7182818284 ...$ と続く超越数を$a$乗したら確率密度になるときの$a$の値ことです。式に表すと $e^a=$pdf です。

# 等差数列を生成
X = np.arange(start=1, stop=7.1, step=0.1)

# logpdfで確率密度関数の対数を生成
norm_logpdf = stats.norm.logpdf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# 可視化
plt.plot(X, norm_logpdf)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("ログ確率密度関数logpdf", fontsize=13)
plt.show()

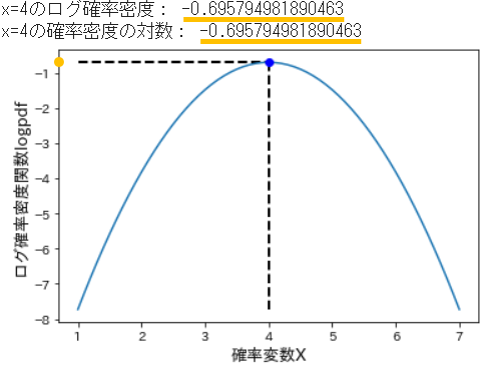
• 試みに、上図で確率密度の対数が最大値を示す確率変数 x=4 について確認してみます。
• 手順としては、まず確率変数 x=4 のログ確率密度の値を取得し、次いで x=4 の確率密度を計算してからその対数をとり、両方を比較します。

# ログ確率密度の最大値を取得
logpdf_max = np.max(norm_logpdf) 
print('x=4のログ確率密度：', logpdf_max)

# 確率密度を計算
x = 4
v_pdf = stats.norm.pdf(x=x, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# 確率密度の対数を計算
v_pdf_log = np.log(v_pdf)
print('x=4の確率密度の対数：', v_pdf_log)

# 可視化
plt.plot(X, norm_logpdf)
plt.plot(4, logpdf_max, 'bo') # 青色ドットを布置

logpdf_min = np.min(norm_logpdf) # ログ確率密度の最小値(描画用)
plt.vlines(x, logpdf_max, logpdf_min, lw=2, linestyles='dashed') # 垂直線
plt.hlines(logpdf_max, 1.0, x, lw=2, linestyles='dashed') # 水平線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("ログ確率密度関数logpdf", fontsize=13)

plt.show()

##➄ cdf (Cumulative distribution function) 累積分布関数

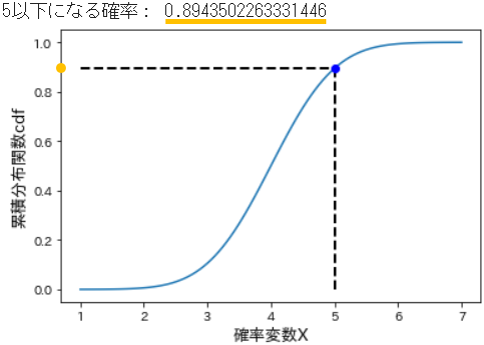
• 記法：cdf(x, loc=0, scale=1)
• 累積分布関数は、確率変数$X$がある値$x$以下となる確率を計算します。
• 例えば、サイコロを投げたときに「出る目が３以下」となる確率は、１から３までの確率密度をすべて足し合わせたものになります。

# x軸の等差数列を生成
X = np.linspace(start=1, stop=7, num=100)

# cdfで累積分布関数を生成
norm_cdf = stats.norm.cdf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# cdfでx=5以下の累積確率を計算
under_5 = stats.norm.cdf(x=5, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8
print('5以下になる確率：', under_5)

# 可視化
plt.plot(X, norm_cdf)
plt.plot(5, under_5, 'bo') # 青色ドットを布置

plt.vlines(5, 0.0, under_5, lw=2, linestyles='dashed') # 垂直線
plt.hlines(under_5, 1.0, 5, lw=2, linestyles='dashed') # 水平線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("累積確率密度cdf", fontsize=13)

plt.show()

• 全く同一のパラメータによる確率密度関数の上に、同じく確率変数 x=5 のポイントを示したのが下図になります。
• 累積分布関数は、この図の水色の領域に相当します。

##➅ sf (Survival function) 生存関数

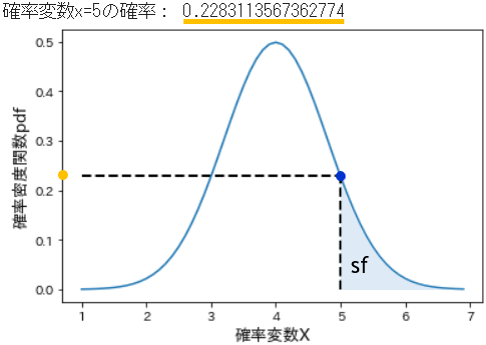
• 記法：sf(x, loc=0, scale=1)
• 生存関数は、累積分布関数cdfとは逆に、確率変数$X$がある値$x$以上となる確率を計算します。
• ｢1-cdf｣ と定義されることもありますが、sfの方がより正確な場合もあるとの指摘がscipy.org https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html に見られます。

# x軸の等差数列を生成
X = np.linspace(start=1, stop=7, num=100)

# sfで生存関数を生成
norm_sf = stats.norm.sf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# sfでx=5以上の累積確率を計算
upper_5 = stats.norm.sf(x=5, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8
print('5以上になる確率：', upper_5)

# 可視化
plt.plot(X, norm_sf)
plt.plot(5, upper_5, 'bo') # 青色ドットを布置

plt.vlines(5, 0.0, upper_5, lw=2, linestyles='dashed') # 垂直線
plt.hlines(upper_5, 1.0, 5, lw=2, linestyles='dashed') # 水平線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("生存関数sf", fontsize=13)

plt.show()

• 全く同一のパラメータによる確率密度関数の上に、同じく確率変数 x=5 のポイントを示したのが下図です。
• 生存関数は、図中の水色の領域に相当します。

##➆ ppf (Percent point function) パーセント点関数

• 記法：ppf(q, loc=0, scale=1)
• パーセント点関数は、累積分布関数cdfの逆関数で、累積分布関数をq％と指定するとその値をとる変数を返します。
• 従って、ppf(0.25)は第１四分位点、ppf(0.5)は中央値にあたる第２四分位点、ppf(0.75)は第３四分位点に相当します。

# x軸の等差数列を生成
X = np.arange(start=1, stop=7, step=0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# ppfで累積分布関数75％に当たる変数を取得
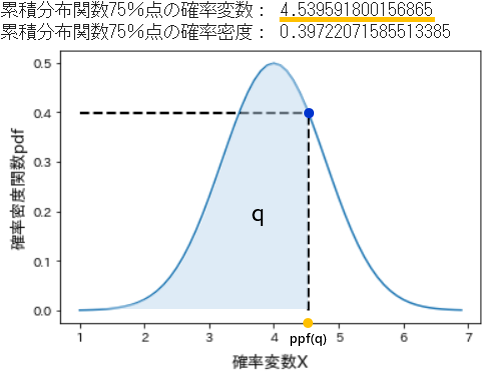
q_75 = stats.norm.ppf(q=0.75, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8
print('累積分布関数75％点の確率変数：', q_75)

# pdfで当該変数の確率密度を取得
v = stats.norm.pdf(x=q_75, loc=4, scale=0.8)
print('累積分布関数75％点の確率密度：', v)

# 可視化
plt.plot(X, norm_pdf)
plt.plot(q_75, v, 'bo') # 青色ドットを布置

plt.vlines(q_75, 0.0, v, lw=2, linestyles='dashed') # 垂直線
plt.hlines(v, 1.0, q_75, lw=2, linestyles='dashed') # 水平線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度関数pdf", fontsize=13)

plt.show()

##➇ isf (Inverse survival function) 逆生存関数

• 記法：isf(q, loc=0, scale=1)
• 逆生存関数は、生存関数sfの逆関数ですが、やることはパーセント点関数ppfと逆のことです。生存関数の残余をq％と指定するとその値をとる変数を返します。
• 従って、四分位点はパーセント点関数ppfとは逆になり、isf(0.25)は第３四分位点、isf(0.5)は同じく第２四分位点、isf(0.75)は第１四分位点に相当します。

# x軸の等差数列を生成
X = np.arange(start=1, stop=7, step=0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# isfで逆生存関数25％に当たる変数を取得
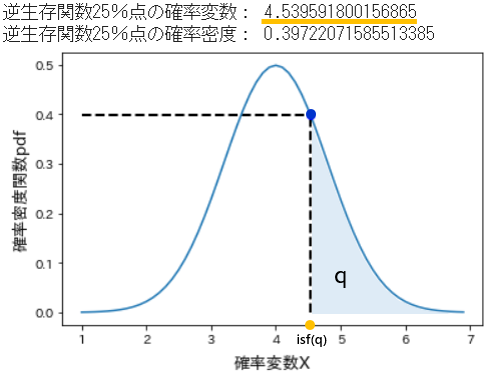
q_25 = stats.norm.isf(q=0.25, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8
print('逆生存関数25％点の確率変数：', q_25)

# pdfで当該変数の確率密度を取得
v = stats.norm.pdf(x=q_25, loc=4, scale=0.8)
print('逆生存関数25％点の確率密度：', v)

# 可視化
plt.plot(X, norm_pdf)
plt.plot(q_25, v, 'bo') # 青色ドットを布置

plt.vlines(q_25, 0.0, v, lw=2, linestyles='dashed') # 垂直線
plt.hlines(v, 1.0, q_25, lw=2, linestyles='dashed') # 水平線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度関数pdf", fontsize=13)

plt.show()

##➈ interval (Endpoints of the range that contains alpha percent of the distribution) 区間推定

• 記法：interval(alpha, loc=0, scale=1)
• 実際のデータから計算される経験分布では、平均値も標準偏差も常に未知のものです。標本から得られた平均値が、母集団における**真の母数$θ$**に近似できているか本当はわかりません。
• そこで、一定の確率のもとに母数$θ$を含む区間を求めることを区間推定といいます。

# x軸の等差数列を生成
X = np.arange(start=1, stop=7, step=0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# intervalで信頼区間95％に当たる変数を取得
lower, upper = stats.norm.interval(alpha=0.95, loc=4, scale=0.8) # 信頼係数=0.95, 期待値=4, 標準偏差=0.8
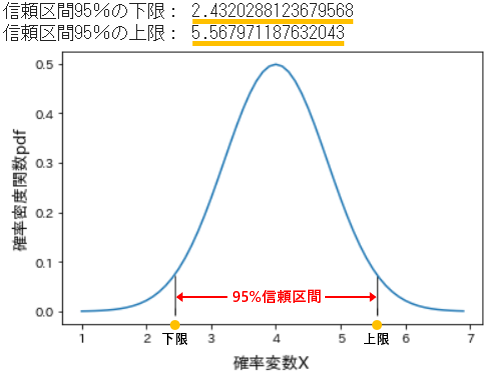
print('信頼区間95％の下限：', lower)
print('信頼区間95％の上限：', upper)

# pdfで各変数の確率密度を取得
v_lower = stats.norm.pdf(x=lower, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8
v_upper = stats.norm.pdf(x=upper, loc=4, scale=0.8) # 期待値=4, 標準偏差=0.8

# 可視化
plt.plot(X, norm_pdf)
plt.plot(lower, 0.0, 'k|')
plt.plot(upper, 0.0, 'k|')

plt.vlines(lower, 0.0, v_lower, lw=0.8) # 下限の垂直線
plt.vlines(upper, 0.0, v_upper, lw=0.8) # 上限の垂直線

plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度関数pdf", fontsize=13)

plt.show()

• 区間推定では、まず母数$θ$を含む区間の確率を指定します。この例ではalpha=0.95がそれで、これを信頼係数と呼びます。多くの場合、99％、95％、90％が使われますが、これは任意です。
• その指定された確率のもとで母数$θ$を含む区間の下限と上限が求められます。この例では95％の確率で、母数$θ$は確率変数が2.43～5.57の間に含まれていることを示しています。

#あとがき

• ログ累積分布関数logcdf、ログ生存関数logsfなどは省きましたが、およそ使用頻度の高そうなものは押さえられたと思います。
• これらを利用して、先に掲げた15種類の確率分布を一つずつ解きほぐしてみたいと思っています。
• 1. Pythonで学ぶ統計学　2-1. 確率分布［離散型変数］