1. Pythonで学ぶ統計学 2-1. 確率分布［離散型変数］

• 離散型の確率変数は、サイコロの目のように飛び飛びの値をとる変数のことで、例えば｢1｣の次は｢2｣、｢2｣の次は｢3｣というように、その間に 1.1, 1.2, 1.3, ･･･, 1.8, 1.9 などといった連続的な数値は存在しません。
• 主な離散型の確率分布について、scipy.statsのpmf（probability mass function : 確率質量関数)やrvs（random variates : 確率変数）を使ってその特徴を見ていきます。

# 数値計算ライブラリのインポート
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
# 可視化ライブラリのインポート
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
%matplotlib inline
# matplotlibの日本語表示モジュール
!pip install japanize-matplotlib
import japanize_matplotlib

##⑴ ベルヌーイ分布（Bernoulli distribution）

• 2種類しかない事象のどちらかを発生させることを**ベルヌーイ試行（Bernoulli trial）**といいます。
• ベルヌーイ分布とは1回のベルヌーイ試行において、それぞれの事象が生じる確率分布のことです。
• 例えば、コインを8回投げて表が出たら0、裏が出たら1として結果を次のように仮定します。

x = np.array([0,0,1,1,0,1,0,0])

# 確率分布を計算
p = len(x[x==1]) / len(x)
pmf_bernoulli = sp.stats.bernoulli.pmf(x, p)

# 可視化
plt.vlines(x, 0, pmf_bernoulli, 
           colors='blue', lw=50)
plt.xticks([0,1])
plt.xlim([0 - 0.5, 1 + 0.5])
plt.grid(True)

2種類の事象	確率
0	0.625
1	0.375

##⑵ 二項分布（Binomial distribution）

• 互いに独立したベルヌーイ試行をn回くり返したとき、ある事象が何回起こるかという確率分布のことを二項分布といいます。
• 例えば、表が出る確率pが50％のコインを5回投げて、そのうち2回が表になる確率をbinom.pmfを使って求めます。

sp.stats.binom.pmf(n=5, p=0.5, k=2)

• 表が出る確率pが20％のコインを10回投げて表が出た回数を数える、という試行を10000回くり返したと仮定し、binom.rvsを使って二項分布に従う疑似乱数を生成します。
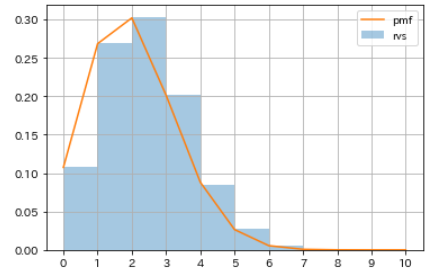
• さらにbinom.pmfを使って、表が出る確率pが20％のコインを10回投げたときに表が出る回数の確率分布を計算し、疑似乱数のヒストグラムと比較してみます。

# 疑似乱数を生成
np.random.seed(1)
rvs_binom = sp.stats.binom.rvs(n=10, p=0.2, size=10000)

# 確率分布を取得
m = np.arange(0, 10+1, 1)
pmf_binom = sp.stats.binom.pmf(n=10, p=0.2, k=m)

# 可視化
sns.distplot(rvs_binom, bins=m, 
             kde=False, norm_hist=True, label='rvs')
plt.plot(m, pmf_binom, label='pmf')
plt.xticks(m)
plt.legend()
plt.grid()

表が出る回数	確率
0	0.107374182
1	0.268435456
2	0.301989888
3	0.201326592
4	0.088080384
5	0.026424115
6	0.005505024
7	0.000786432
8	0.000073728
9	0.000004096
10	0.000000102

##⑶ ポアソン分布（Poisson distribution）

• ごく稀に起こる事象の確率で、例えば単位面積当たりの雨粒の数とか、ある交差点で一年間に発生する事故の回数などがポアソン分布に従います。
• つまり、一定の時間や面積に対して一定の割合で発生する確率分布で、サンプル数nが十分に大きく確率pが非常に小さい場合です。
• 例えば、ある期間に平均5回起こる現象が2回だけ起こる確率をpoisson.pmfを使って求めます。

sp.stats.poisson.pmf(k=2, mu=5)

• ポアソン分布のパラメータはある事象の平均発生回数muで、これは強度とか**λ（ラムダ）**とも呼ばれます。
• ある事象が起こる確率pを20％として、起こった回数を数えるという試行を10000回くり返したと仮定し、poisson.rvsを使ってポアソン分布に従う疑似乱数を生成します。
• さらにpoisson.pmfを使って、発生確率pが20％のときの確率分布を計算し、疑似乱数のヒストグラムと比較してみます。

# 疑似乱数を生成
np.random.seed(1)
rvs_poisson = sp.stats.poisson.rvs(mu=2, size=10000)

# 確率分布を取得
m = np.arange(0, 10+1, 1)
pmf_poisson = sp.stats.poisson.pmf(mu=2, k=m)

# 可視化
sns.distplot(rvs_poisson, bins=m, 
             kde=False, norm_hist=True, label='rvs')
plt.plot(m, pmf_poisson, label='pmf')
plt.xticks(m)
plt.legend()
plt.grid()

発生回数	確率
0	0.135335283
1	0.270670566
2	0.270670566
3	0.180447044
4	0.090223522
5	0.036089409
6	0.012029803
7	0.003437087
8	0.000859272
9	0.000190949
10	0.000038190

• ここで、ポアソン分布と二項分布の関係を考察します。
• 試行回数nが十分に大きく確率pが非常に小さいときの二項分布の確率分布を計算し、先のポアソン分布の例と比較してみます。

# パラメータを指定
n = 100000000
p = 0.00000002

# 二項分布の確率分布を計算
num = np.arange(0, 10+1, 1)
pmf_binom_2 = sp.stats.binom.pmf(n=n, p=p, k=num)

# 可視化
plt.plot(m, pmf_poisson, 
         color='lightgray', lw=10, label='poisson')
plt.plot(m, pmf_binom_2, 
         color='black', linestyle='dotted', label='binomial')
plt.xticks(num)
plt.legend()
plt.grid()

• この場合、ポアソン分布と二項分布はほぼ一致し、両者が近い関係にあることがわかります。
• ポアソン分布は、二項分布の発生確率pが非常に小さく試行回数nが十分に大きいときの状況を近似的に表します。

⑷ 幾何分布（geometric distribution）

• 成功確率がpの独立したベルヌーイ試行をくり返すとき、初めて成功するまでの試行回数kが従う確率分布を幾何分布といいます。
• 例えば、サイコロを１回だけ投げて「1」が出る確率をscipy.statsのgeom.pmfを使って取得します。

%precision 3
sp.stats.geom.pmf(k=1, p=1/6)

• サイコロの目は全部で6つ、すべてが同じ確率とすれば 1/6 で 0.167 になるのは当然ですが、
• 次々と投げて、2回目に初めて｢1｣が出る確率、3回目に初めて｢1｣が出る確率、･･････、10回目に初めて｢1｣が出る確率を求めます。

# 試行回数を指定
num = np.arange(1, 11, 1)

# 確率分布を計算
prob = []
for i in num:
    value = sp.stats.geom.pmf(k=i, p=1/6)
    prob.append(value)

# 可視化
plt.bar(num, prob)
plt.xticks(num)
plt.xlabel('初めて1が出るまでの回数')
plt.ylabel('確率')
plt.show()

• k回投げて、k-1回目までは失敗し、k回目に初めて成功する確率ということで、この場合の確率分布は次の通りです。

試行回数	確率	計算式
1	0.167	⅙
2	0.139	⅚・⅙
3	0.116	⅚・⅚・⅙
4	0.096	⅚・⅚・⅚・⅙
5	0.080	⅚・⅚・⅚・⅚・⅙
6	0.067	⅚・⅚・⅚・⅚・⅚・⅙
7	0.056	⅚・⅚・⅚・⅚・⅚・⅚・⅙
8	0.047	⅚・⅚・⅚・⅚・⅚・⅚・⅚・⅙
9	0.039	⅚・⅚・⅚・⅚・⅚・⅚・⅚・⅚・⅙
10	0.032	⅚・⅚・⅚・⅚・⅚・⅚・⅚・⅚・⅚・⅙

##⑸ 離散一様分布（uniform distribution）

• 一様分布には離散型と連続型があり、確率変数が離散型の一様分布を離散一様分布といいます。
• すべての事象の起こる確率が等しい分布で、例えばサイコロは1から6までの目が出る確率がすべて等しいので離散一様分布に従います。

# 全事象を指定
num = np.arange(1, 7, 1)

# 確率分布を計算
prob = []
for i in num:
    value = 1 / len(num)
    prob.append(value)

# 可視化
plt.bar(num, prob)
plt.xticks(num)
plt.xlabel('サイコロの目')
plt.ylabel('確率')
plt.show()

サイコロの目	確率
1	0.167
2	0.167
3	0.167
4	0.167
5	0.167
6	0.167

##⑹ 超幾何分布（hypergeometric distribution）

• 例えば、全部で20個のくじがあり、そのうち7個が当たりであるとします。20個からランダムに12個を選んだとき、当たりが何個出るか。
• この「引き当てる個数」を確率変数とする分布を超幾何分布といいます。
• パラメータは3つで、全体の個数M、当たりの個数n、選択する個数Nになります。

# パラメータを指定
M = 20 #全体個数
n = 7  #当たり個数
N = 12 #選択個数

# 確率変数を作成
k = np.arange(0, n+1)

# モデルを作成
hgeom = sp.stats.hypergeom(M, n, N)
# 確率分布を計算
pmf_hgeom = hgeom.pmf(k)

# 可視化
plt.bar(k, pmf_hgeom)
plt.xticks(k)
plt.xlabel('当たりの個数')
plt.ylabel('確率')
plt.show()

当たり個数	確率
0	0.00010
1	0.00433
2	0.04768
3	0.19866
4	0.35759
5	0.28607
6	0.09536
7	0.01022

##⑺ 負の二項分布（negative binomial distribution）

• 負の二項分布では、n回の試行でk回成功する確率を求め、最後の試行が成功であることを条件とします。
• 二項分布では成功回数kが確率変数ですが、負の二項分布では成功回数kは固定です。確率変数には、試行回数nを使う代わりに失敗の数n-kを使います。
• 例えば、コイントスをくり返して3回表が出るまでに何回投げる必要があるか。すなわち3回成功するまでに何回失敗する必要があるか、という失敗回数が確率変数になります。

# パラメータを指定
N = 12  #試行回数
p = 0.5 #成功確率
k = 3   #成功回数

# 確率分布を計算
pmf_nbinom = sp.stats.nbinom.pmf(range(N), k, p)

# 可視化
plt.bar(range(N), pmf_nbinom)
plt.xlabel('失敗の回数')
plt.ylabel('確率')
plt.xticks(range(N))
plt.show()

失敗の回数	確率
0	0.125
1	0.188
2	0.188
3	0.156
4	0.117
5	0.082
6	0.055
7	0.035
8	0.022
9	0.013
10	0.008
11	0.005

##まとめ
離散型の確率分布を見てきましたが、何が確率変数となるのか、平たく言えばx軸に何を置くかという点を意識して一覧表にまとめます。

	確率分布の種類	確率変数	パラメータ
⑴	ベルヌーイ分布	事象0, 1	発生確率p
⑵	二項分布	試行の回数	発生確率p, 発生回数k, 試行回数n
⑶	ポアソン分布	試行の回数	平均発生回数mu
⑷	幾何分布	試行の回数	成功確率p, 試行回数k
⑸	離散一様分布	事象の種類	※scipy.atatsの一様分布は連続型のみ
⑹	超幾何分布	成功の個数	全体個数M, 全体中の成功個数n, 選択個数N
⑺	負の二項分布	失敗の回数	成功確率p, 成功回数k, 試行回数N