【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸(円弧)

XZ軸(Cos波)

YZ軸(Sin波)

この様に三角関数_Cos(θ)_と三角関数_Sin(θ)_は位相が_π/2ラジアン(90度)_ズレているだけの同じ波なので、以下の数値積分(Numerical integration)の結果に互換性があったりするのです。
1/4周分の面積の合計は「1」
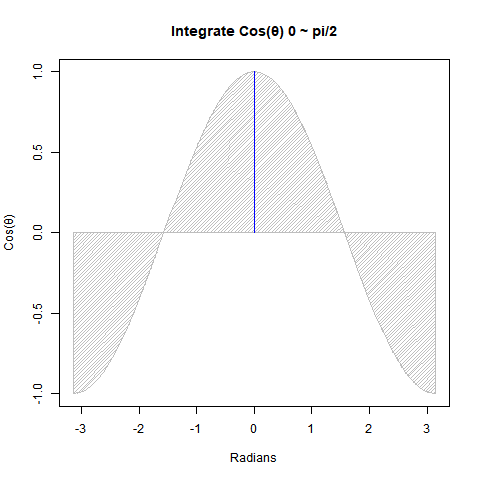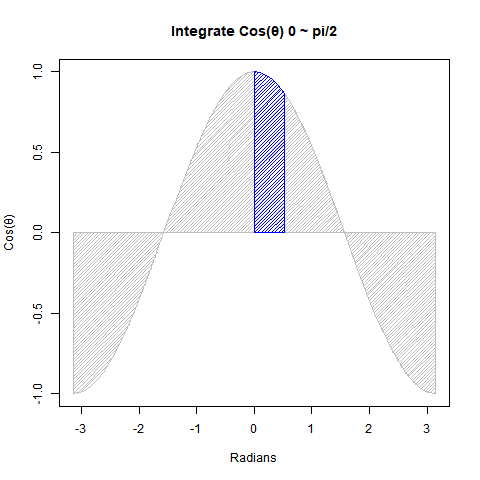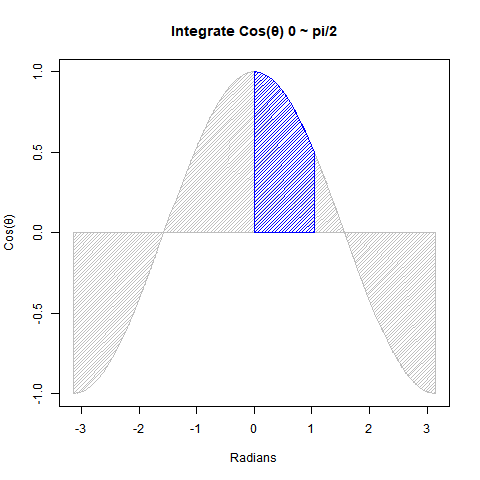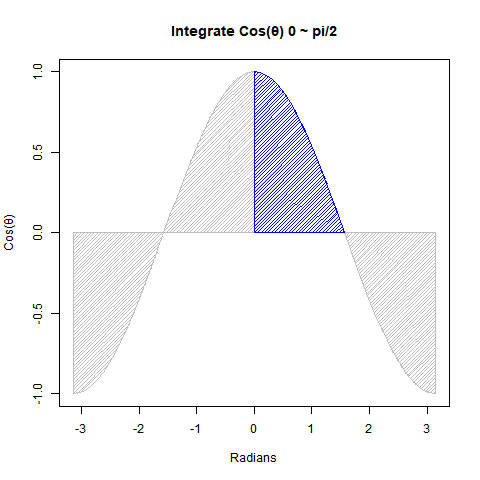
①Cos(θ)を0からπ/2ラジアン(90度)まで数値積分すると1なる。
# 0からpi/2にかけてのcos(ΔΘ)の積層結果(数値積分)
integrate(cos,0,pi/2)
1 with absolute error < 1.1e-14
# NIQC=Numerical Integration of Quarter Cosine wave
NIQC<-function(Radian){
st_Radian<-31
cx<-seq(-pi,pi,length=61)
cy<-cos(cx)
plot(cx,cy,type="l",xlim=c(-pi,pi),ylim=c(-1,1),main="Integrate Cos(θ) 0 ~ pi/2",xlab="Radians",ylab="Cos(θ)")
# 塗りつぶし(背景)
polygon(c(-pi,cx,pi), #x
c(0,cy,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(Cos波)
polygon(c(0,cx[st_Radian:Radian],cx[Radian]), #x
c(0,cy[st_Radian:Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
}
# アニメーション
library("animation")
Time_Code=c(31:46)
saveGIF({
for (i in Time_Code){
NIQC(i)
}
}, interval = 0.1, movie.name = "NIQC01.gif")
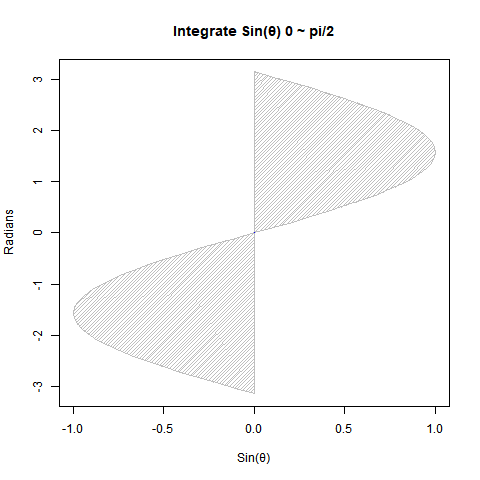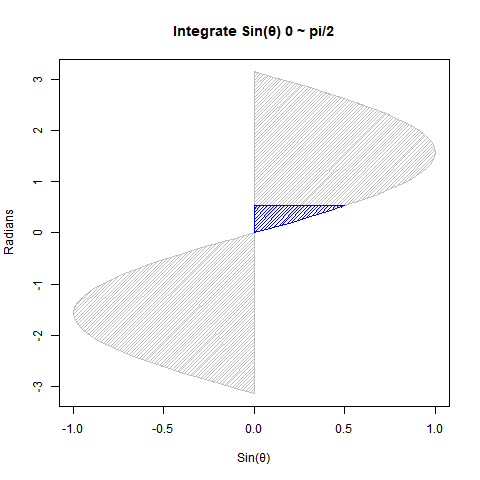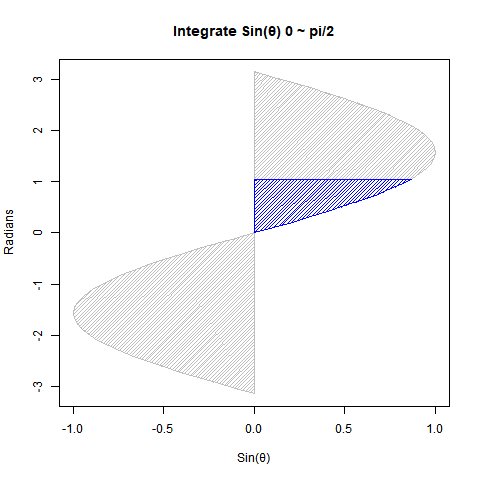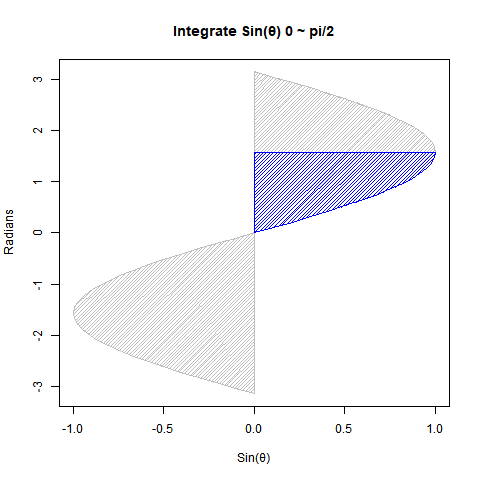
②Sin(θ)を0からπ/2ラジアン(90度)まで数値積分しても1なる。
# 0からpiにかけてのsin(ΔΘ)の積層結果(数値積分)
integrate(sin,0,pi/2)
1 with absolute error < 1.1e-14
# NIQS=Numerical Integration of Quarter Sine wave
NIQS<-function(Radian){
st_Radian<-31
cx<-seq(-pi,pi,length=61)
cy<-sin(cx)
plot(cy,cx,type="l",xlim=c(-1,1),ylim=c(-pi,pi),main="Integrate Sin(θ) 0 ~ pi/2",xlab="Sin(θ)",ylab="Radians")
# 塗りつぶし(背景)
polygon(c(0,cy,0), #x
c(-pi,cx,pi), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(Sin波)
polygon(c(0,cy[st_Radian:Radian],0), #x
c(0,cx[st_Radian:Radian],cx[Radian]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
}
# アニメーション
library("animation")
Time_Code=c(31:46)
saveGIF({
for (i in Time_Code){
NIQS(i)
}
}, interval = 0.1, movie.name = "NIQS01.gif")
1/2周分の面積の合計は「2」
①Cos(θ)を-π/2ラジアン(90度)からπ/2ラジアン(90度)まで数値積分すると2となる。
# -pi/2からpi/2にかけてのcos(ΔΘ)の積層結果(数値積分)
integrate(cos,-pi/2,pi/2)
2 with absolute error < 2.2e-14
# NIHC=Numerical Integration of Harf Cosine wave
NIHC<-function(Radian){
st_Radian<-16
cx<-seq(-pi,pi,length=61)
cy<-cos(cx)
plot(cx,cy,type="l",xlim=c(-pi,pi),ylim=c(-1,1),main="Integrate Cos(θ) -pi/2 ~ pi/2",xlab="Radians",ylab="Cos(θ)")
# 塗りつぶし(背景)
polygon(c(-pi,cx,pi), #x
c(0,cy,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(Cos波)
polygon(c(cx[st_Radian],cx[st_Radian:Radian],cx[Radian]), #x
c(0,cy[st_Radian:Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
}
# アニメーション
library("animation")
Time_Code=c(16:46)
saveGIF({
for (i in Time_Code){
NIHC(i)
}
}, interval = 0.1, movie.name = "NIHC01.gif")
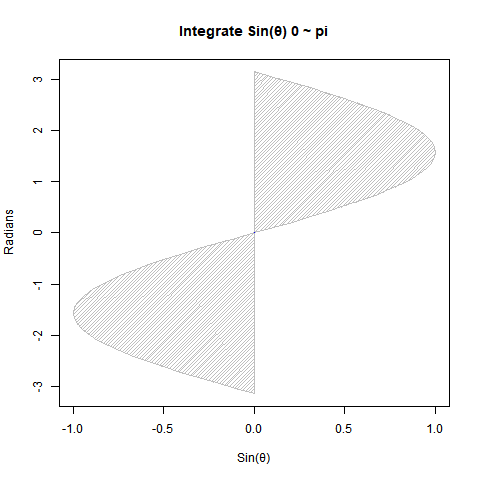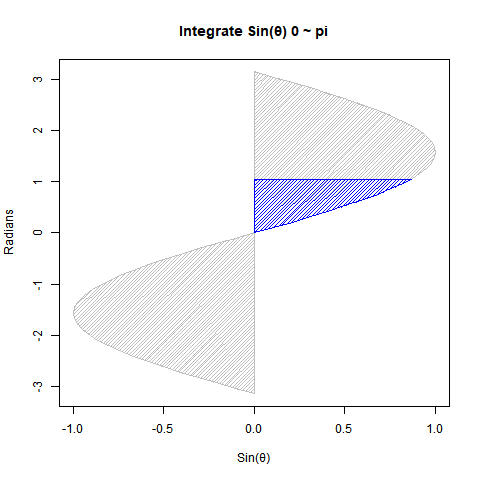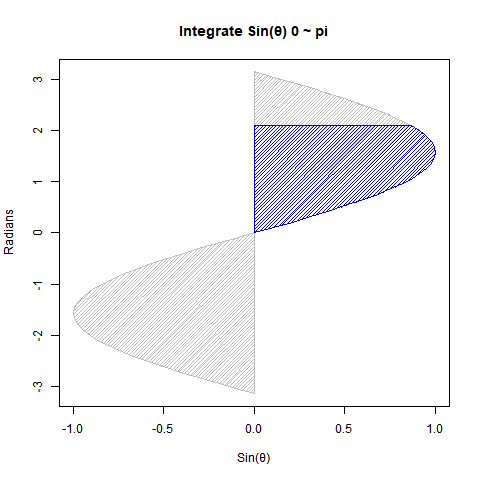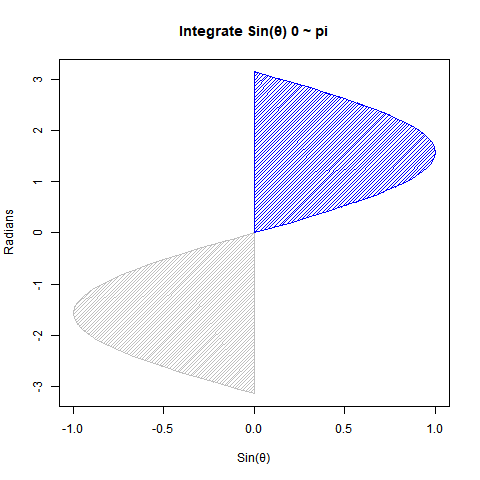
②Sin(θ)を0ラジアン(0度)からπラジアン(180度)まで数値積分しても2となる。
# 0からpiにかけてのsos(ΔΘ)の積層結果(数値積分)
integrate(sin,0,pi)
2 with absolute error < 2.2e-14
# NIQS=Numerical Integration of Harf Sine wave
NIHS<-function(Radian){
st_Radian<-31
cx<-seq(-pi,pi,length=61)
cy<-sin(cx)
plot(cy,cx,type="l",xlim=c(-1,1),ylim=c(-pi,pi),main="Integrate Sin(θ) 0 ~ pi",xlab="Sin(θ)",ylab="Radians")
# 塗りつぶし(背景)
polygon(c(0,cy,0), #x
c(-pi,cx,pi), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(Sin波)
polygon(c(0,cy[st_Radian:Radian],0), #x
c(0,cx[st_Radian:Radian],cx[Radian]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
}
# アニメーション
library("animation")
Time_Code=c(31:61)
saveGIF({
for (i in Time_Code){
NIHS(i)
}
}, interval = 0.1, movie.name = "NIHS01.gif")
概ね円弧や球面の数値積分に絡んでくるのはこの辺り。それぞれの三角関数の残りの部分は符号がマイナスの同面積なので単純に足し合わせると_0_,絶対値を合計すると_4_となります。以下続報…