【Python画像処理】メルカトル図法(Mercator Projection)と正距方位図法（Azimuthal Equidistant Projection）

まずは最初に、以下で使う2種類のテクスチャーを用意します。

元画像(メルカトル図法による世界地図)

アスペクト比1:1

アスペクト比1:2

%matplotlib nbagg
import cv2
import matplotlib.pyplot as plt
import numpy as np

#イメージ読み込み関数
def open_img(file_name):
    img = cv2.imread(file_name,-1)[:,:,::-1]
    height, width, channels = img.shape[:3]
    if channels == 3:  # RGBならアルファチャンネル追加
        image = cv2.cvtColor(img, cv2.COLOR_RGB2RGBA)
    return img

#世界地図(オリジナル)
img_org = open_img("worldmap.png")
height, width, channels = img_org.shape[:3]
plt.imshow(img_org)
plt.show()

#矩形(リサイズ1:1)チャンネル数が4から3に減ってしまう。
img_resize=cv2.resize(img_org, (height,height))
plt.imshow(img_resize)
plt.show()

#矩形(リサイズ1;2)チャンネル数が4から3に減ってしまう。
img_resize=cv2.resize(img_org, (height*2,height))
plt.imshow(img_resize)
plt.show()

#メルカトル図法(Mercator Projection)と指数/対数写像(Exponential/Logarithmic Map)
メルカトル図法 - Wikipedia

1569年にフランドル（現ベルギー）出身の地理学者ゲラルドゥス・メルカトルがデュースブルク（現ドイツ）で発表した地図に使われた投影法である。図の性質と作成方法から正角円筒図法ともいう。等角航路が直線で表されるため、海図・航路用地図として使われてきた。メルカトルが発案者というわけではなく、ドイツのエアハルト・エッツラウプが1511年に作成した地図にはすでに使われていた。

なぜ、メルカトル図法は全世界に普及したのか？

正角図法の一種であるメルカトル図法では経線と緯線が直行し、緯線同士、経線同士が平行となります。その正角性を保持するため、緯線と経線の拡大率を一致することが求められ、極地方に行くにしたがって1度当たりの緯線の長さが増大し、経線も同様に拡大します。その結果より北にあるグリーンランドは島でありながら、大陸であるオーストラリアより地図上では大きく見えるのです。

等角航路

航路の出発地と目的地を結んでできる直線と経線からできる角度がコースのどの地点でも一定で(風や潮流の影響を加味しながら)羅針盤の示す角度に従って航海すれば自船の位置を気にする事なく目的地に到達出来ます。このように2点間を結んだ直線上の航路を一定の角度で航行し目的地に到着する航路を等角航路といいます。自船の位置を求めるのが困難だった時代にはこれが簡単に設定可能である事が重宝され、広く普及したのです。

大圏航路

一方、2点間を最短距離で結ぶ大圏航路は燃料消費や移動時間といった面で優れている一方、移動する自船の位置によって航路上でも進行方向をその位置ごとの適切な角度に調整する必要があり、ナビゲーションシステム等がない限り、実際に航行するのは難しかったのです。

これは(縦軸に加法群、横軸にその指数写像たる乗法群を置く円筒座標系としての)実数環(Real Ring)上で考えると高さπr($±\frac{π}{2}$)、幅2πr(±π)のアスペクト比1:2の円筒を半径rの球面に射映した指数写像に該当します(この円筒の側面積$2π^2r^2$をπについて微分→球表面の面積$4πr^2$)。
【Python演算処理】環論に立脚した全体像再構築①空環と実数環

	XY座標(水平軸=半径)	Z座標(垂直軸=高さ)
0	半径0(円筒の場合1)	高さ0(-1)
1	半径1(円筒の場合1)	高さ1(0)
2	半径0(円筒の場合1)	高さ2(-1)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["半径0(円筒の場合1)","半径1(円筒の場合1)","半径0(円筒の場合1)"],
    ["高さ0(-1)","高さ1(0)","高さ2(-1)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['XY座標(水平軸=半径)', 'Z座標(垂直軸=高さ)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

Pythonで好きな画像を球に張り付ける！
matplotlib - plot_surface で 3D グラフを描画する方法

%matplotlib nbagg
import cv2
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#イメージ読み込み関数
def open_img(file_name):
    img = cv2.imread(file_name,-1)[:,:,::-1]
    height, width, channels = img.shape[:3]
    if channels == 3:  # RGBならアルファチャンネル追加
        image = cv2.cvtColor(img, cv2.COLOR_RGB2RGBA)
    return img

#画像の読み込みと平方化
img_org = open_img("worldmap.png")
height, width, channels = img_org.shape[:3]
img_resize=cv2.resize(img_org, (height,height))

#RGBの範囲は0~1の値をとるため、256で割る作業をする。
mm = np.array(img_resize)/256.

#緯度経度の指定
radius = 1
long = np.linspace(0, 2*np.pi, mm.shape[1])
lat = np.linspace(-np.pi/2, np.pi/2, mm.shape[0])[::-1]
lat2, long2 = np.meshgrid(lat, long)
X = (radius*np.cos(lat2)*np.cos(long2)).T
Y = (radius*np.cos(lat2)*np.sin(long2)).T
Z = (radius*np.sin(lat2)).T

#グラフ表示
plt.style.use('default')
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot( 111 , projection='3d')

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot_surface(X, Y, Z, facecolors = mm, shade=False, rstride=1, cstride=1)
    #諸元追加
    rmax = 1.5
    ax.set_xlim(-rmax,rmax)
    ax.set_ylim(-rmax,rmax)
    ax.set_zlim(-rmax,rmax)
    ax.set_title("World Map")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=45(360-45),elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=np.arange(0,360,6)  
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("wm0001.gif", writer="pillow")

「側面」からの射映

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].real,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.imag,color="gray",lw=0.5)
        ax.plot(rollxy.real,rollxy.imag,Ed.imag,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].imag,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    ax.plot(rollc.real,rollc.imag,-rollz,color="black",lw=0.5)
    #円筒追加
    #ax.plot(uc.real*np.pi,uc.imag*np.pi,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi/2,np.pi/2])
    ax.set_xlim([-np.pi/2,np.pi/2])
    ax.set_zlim([-np.pi/2,np.pi/2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1/2
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map1100001.gif", writer="pillow")

#正距方位図法（Azimuthal Equidistant Projection）と指数/対数写像①半球の場合

ところで上掲の地球儀の上面図と下面図は以下となっており、それぞれ北極もしくは南極を始点に赤道まで最短距離=直線で到達する大圏航路を示しています。

	半円筒	北半球
0	高さ0(半径1)	高さ0(半径1)
1	高さπ/2(半径1)	高さ1(半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["高さ0(半径1)","高さπ/2(半径1)"],
    ["高さ0(半径1)","高さ1(半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['半円筒', '北半球'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

「底面」からの写像

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.imag,rollxy.real,Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,-rollz,color="black",lw=0.5)
    #円筒追加
    #ax.plot(uc.real*np.pi,uc.imag*np.pi,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi/2,np.pi/2])
    ax.set_xlim([-np.pi/2,np.pi/2])
    ax.set_zlim([-np.pi/2,np.pi/2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1/2
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map600001.gif", writer="pillow")

「側面」からの写像

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].real,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,Ed.imag,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].imag,len(rollc))
    ax.plot(rollc.real,rollc.imag,-rollz,color="black",lw=0.5)
    #円筒追加
    #ax.plot(uc.real*np.pi,uc.imag*np.pi,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi/2,np.pi/2])
    ax.set_xlim([-np.pi/2,np.pi/2])
    ax.set_zlim([-np.pi/2,np.pi/2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1/2
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map800001.gif", writer="pillow")

	半円筒	南半球
0	高さ0(半径1)	高さ0(半径1)
1	高さ-π/2(半径1)	高さ-1(半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["高さ0(半径1)","高さ-π/2(半径1)"],
    ["高さ0(半径1)","高さ-1(半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['半円筒', '南半球'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

「底面」からの写像

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.imag,rollxy.real,-Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    #ax.plot(uc.real*np.pi,uc.imag*np.pi,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi/2,np.pi/2])
    ax.set_xlim([-np.pi/2,np.pi/2])
    ax.set_zlim([-np.pi/2,np.pi/2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1/2
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map700001.gif", writer="pillow")

「側面」からの写像

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].real,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.imag,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].imag,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    #ax.plot(uc.real*np.pi,uc.imag*np.pi,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi/2,np.pi/2])
    ax.set_xlim([-np.pi/2,np.pi/2])
    ax.set_zlim([-np.pi/2,np.pi/2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1/2
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map900001.gif", writer="pillow")

• 半球に指数写像として射映されるのが「距離1だけ原点から離れた半径$\frac{π}{2}$の円盤」でも「高さ$\frac{π}{2}$の円筒側面」でも同じ結果を迎える多価性が興味深い。そう、実は両者は実数環座標系において水平軸上のX座標(Y座標)を垂直軸上のZ座標と置換(Permutation)した対照群(Symmetric Group)にまとめられたりもする？
  対称群 -Wikipedia
• そしてかかる射映の結果現れる極座標的球面座標系(Polar Coordinate Spherical Coordinate System)はXY面、XZ面、YZ面それぞれから観察した(隠された裏面が見えてる表面と完全に一致する)複素共役概念(Complex Conjugate)に完全に一致する。
  【初心者向け】複素共役のアニメーション表示について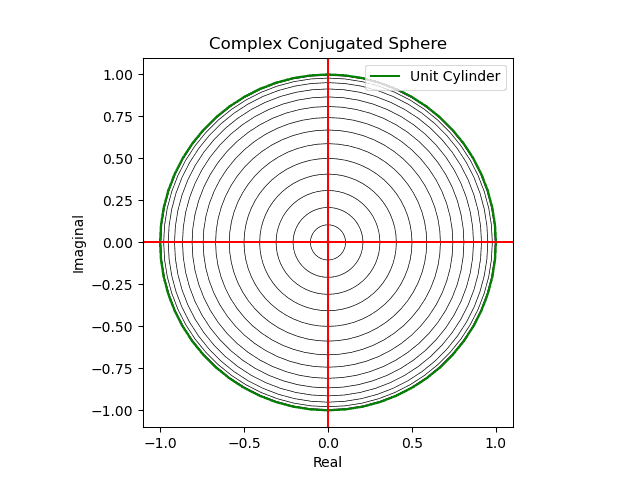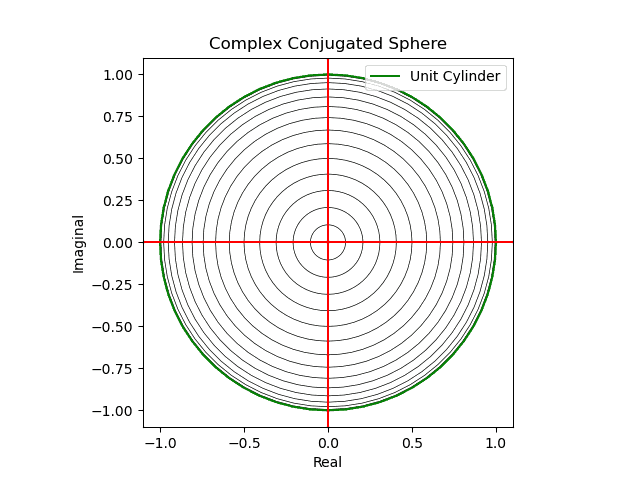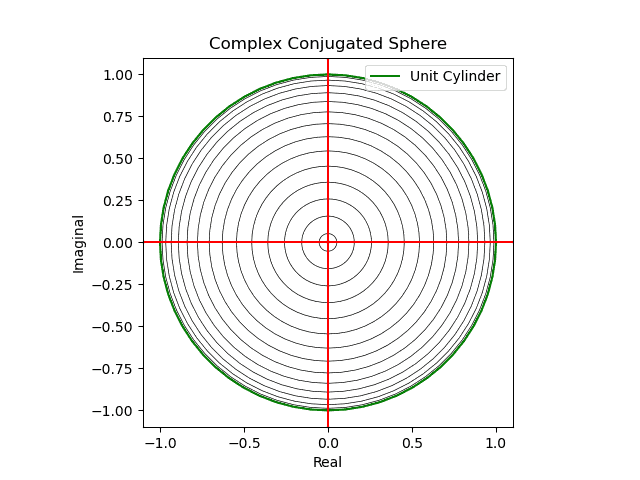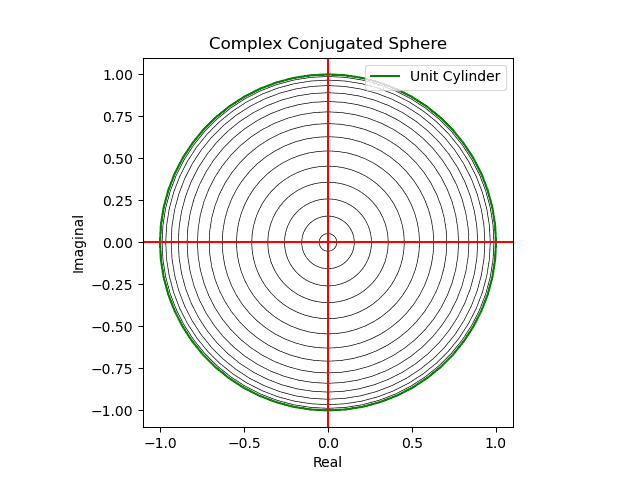
  
  
  

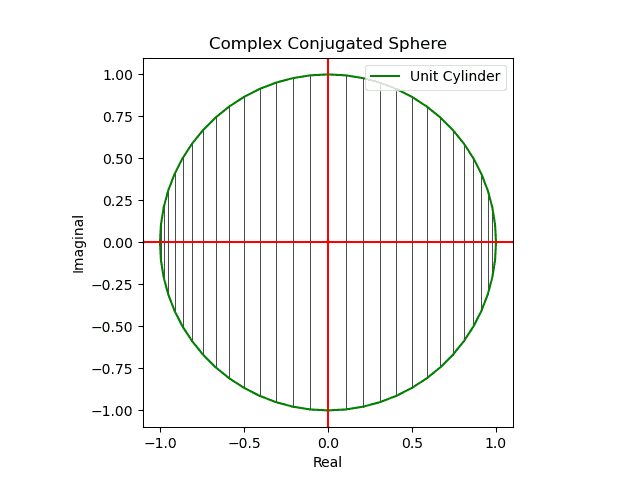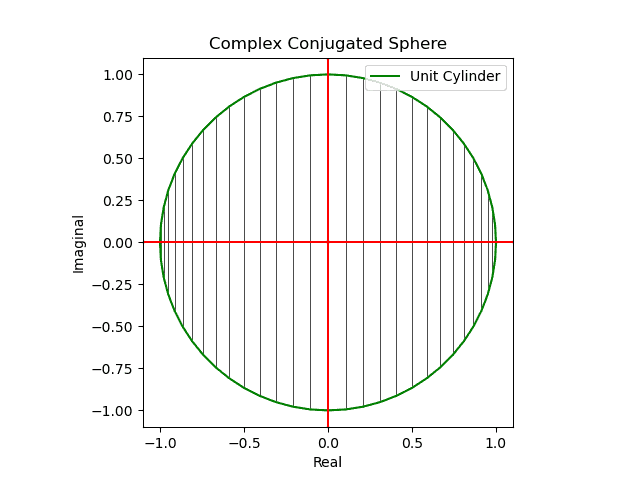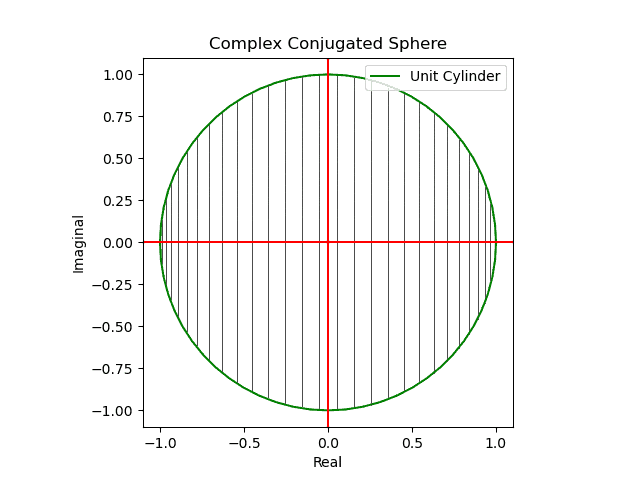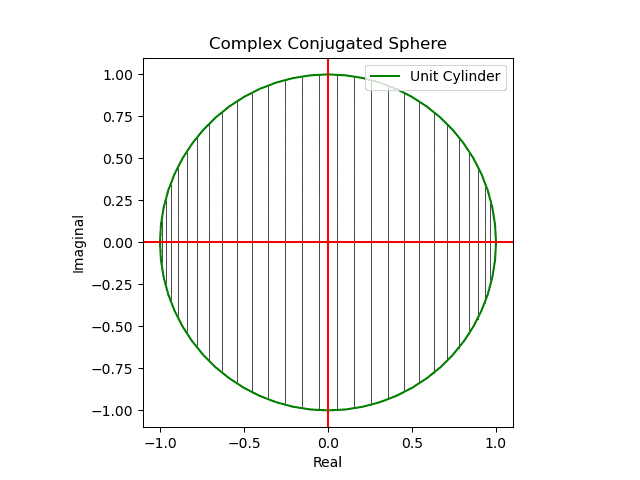
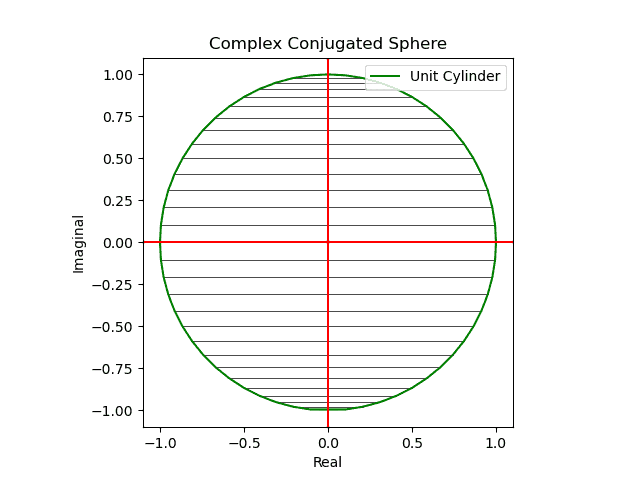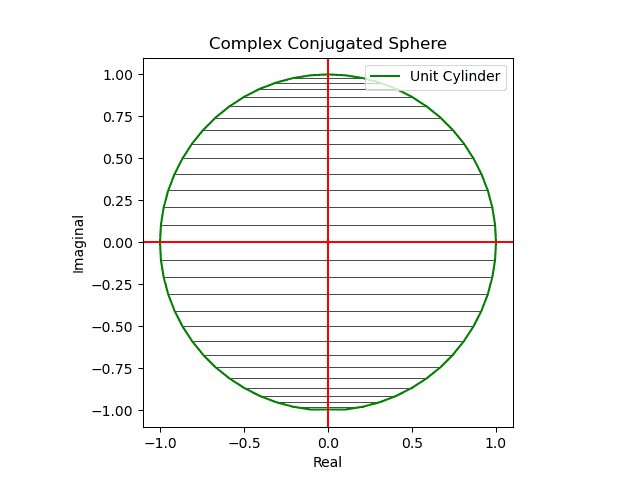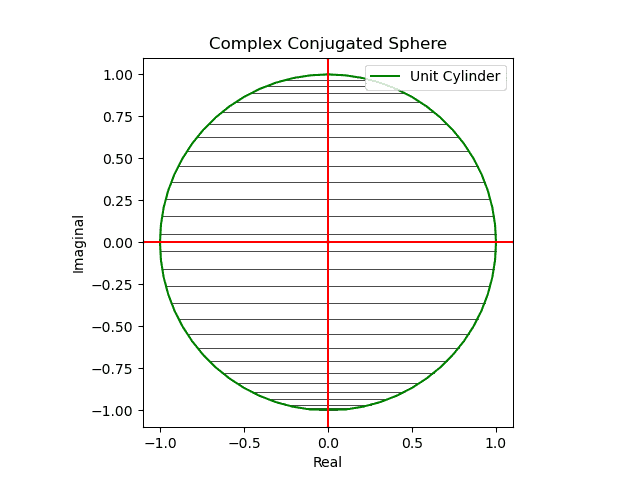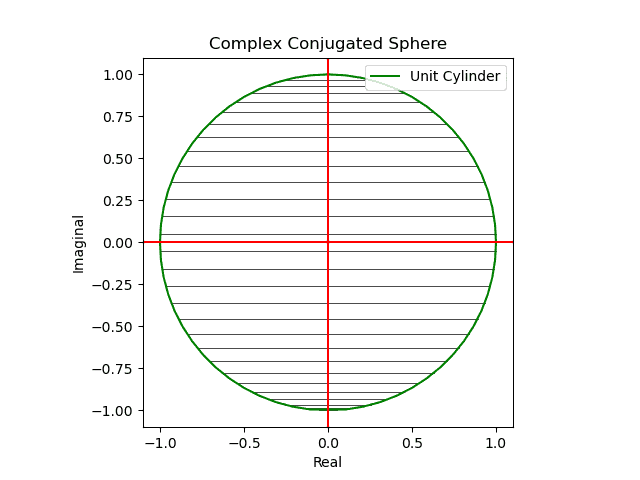
メルカトル図法が「船の時代の航路」の産物とすれば、こちらは「飛行機の時代の航路」の産物。かかる図法を正距方位図法（Azimuthal Equidistant Projection）といいます。

正距方位図法 - Wikipedia

中心からの距離と方位が正しく記され、地球全体が真円で表される投影法で、大圏航路(飛行機の最短経路）や出発点からの方位を見るために使われる。中心に対し地球の裏側に当たる一点（対蹠地）が円周となるが、円周に近づくほど引き伸ばされて歪みが大きくなる。

そう、まさにここでいう「(人間の認識可能範囲を超越する)歪みの拡大」こそが以降、問題となってくるのです。

#正距方位図法（Azimuthal Equidistant Projection）と指数/対数写像②全球の場合

当然上掲の考え方は「全球に対する半径πの円盤の射映」へと拡張可能です。

正距方位図法 - Wikipedia

【Pyrhon演算処理】同心集合③環概念と指数/対数写像概念の導入

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,Ed.real+1,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz+1,color="black",lw=0.5)
    ax.plot(rollc.real/2,rollc.imag/2,rollz/2+1,color="green",lw=0.5)   
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz1,color="blue",lw=1)
    ax.plot(uc.real*np.pi/2,uc.imag*np.pi/2,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([-np.pi,np.pi])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map110005.gif", writer="pillow")

半径1の単位円を中心に北極に観測原点0($e^{-∞}=\frac{1}{∞}$)、南極に観測限界∞($e^{+∞}$)を配した乗法群系座標モデルの一つであるリーマン円錐/球面も、こうした座標系のバリエーションの一つとして現れてきます。
リーマン球面 - Wikipedia

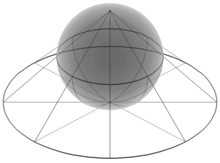
本来の半径1の円筒座標系(縦軸が等尺の実数列)から円錐座標系(縦軸=指数尺)への写像

	実数列(円筒座標系の縦軸,等尺)	円錐座標系の縦軸(指数尺)
0	-∞(半径1)	0(半径0)
1	-1(半径1)	exp(-1)
2	0(半径1)	1(半径1)
3	1(半径1)	exp(+1)
4	+∞(半径1)	∞(半径∞)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-∞(半径1)","-1(半径1)","0(半径1)","1(半径1)","+∞(半径1)"],
    ["0(半径0)","exp(-1)","1(半径1)","exp(+1)","∞(半径∞)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', '円錐座標系の縦軸(指数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

図の「特殊円錐座標系」で遂行されている写像

	実数列(円筒座標系の縦軸,等尺)	特殊円錐座標系の縦軸(両側対数尺)
0	-∞(半径1)	0(半径0)
1	0(半径1)	1(半径1)
2	+∞(半径1)	2(半径π)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-∞(半径1)","0(半径1)","+∞(半径1)"],
    ["0(半径0)","1(半径1)","2(半径π)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', '特殊円錐座標系の縦軸(両側対数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

「リーマン球面」への写像

	実数列(円筒座標系の縦軸,等尺)	リーマン球面の縦軸(両側対数尺)
0	-∞(半径1)	0(半径0)
1	0(半径1)	1(半径1)
2	+∞(半径1)	2(半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-∞(半径1)","0(半径1)","+∞(半径1)"],
    ["0(半径0)","1(半径1)","2(半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', 'リーマン球面の縦軸(両側対数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

いずれにせよ、これらの座標系に射映されるMapping Dataは以下となる様です。

	リーマン円錐/球面の高さ	リーマン円錐/球面の写像
0	0(-1)	半径0
1	1(0)	半径π/2
2	2(+1)	半径π

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["0(-1)","1(0)","2(+1)"],
    ["半径0","半径π/2","半径π"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['リーマン円錐/球面の高さ', 'リーマン円錐/球面の写像'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

#トーラス座標系(Torus Coordinate System)と指数/対数写像

一方、アスペクト比1:1のMapは幅と高さがそれぞれ2πとなるトーラス座標系(Torus Coordinate System)に登場します。
【Python演算処理】環論に立脚した全体像再構築①空環と実数環

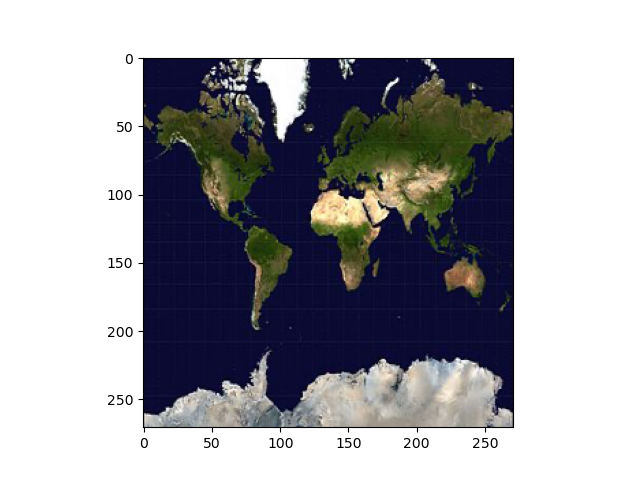
「(逆関数の演算結果集合も完全に閉じた元内に収まる偶関数と異なり)奇関数には逆関数が存在する」とは、要するにこういう事である。

ここで現れる2つの球面を回転させるとトーラス座標系(Torus Coordinate System)に発展する。

このアニメーションにおける赤い円弧の動きは「(コンピューターRPGの世界マップの様な)2π×2πの面積を有する平坦トーラス(Flat Torus)のどちらかの軸を二次元トーラスの大半径に射映すると、もう一方の軸上の移動が小半径上の回転(x軸上の0から2にかけての動き)に射映される」状況を表しているのです。
RPG世界の形状についての幾何学的考察と可視化

ここに例示した(大半径と小半径の組み合わせで表現される)二次元トーラスの一種としての単位トーラス(Unit Torus=大半径も小半径も1の二次元トーラス)は、1次元球面(半径1の単位円)=円周群(Circle Group)$\mathbb{T}$=特殊直交群(Special Orthogonal Group)SO(2)=複素1次ユニタリ群(Unitary Group)U(1)=リー群$S^1$の直積(Direct Product)たるリー群$S^2$と規定され、さらにもう１回直積を取った結果が三次元トーラス=リー群$S^3$=四元数(Quaternion)a+bi+cj+dkの純虚部となる。

【数理考古学】群論とシミュレーション原理⑦三次元トーラスとしての四元数概念導入

• 1次元球面(半径1の単位円)=円周群(Circle Group)$\mathbb{T}$=特殊直交群(Special Orthogonal Group)SO(2)=複素1次ユニタリ群(Unitary Group)U(1)=リー群$S^1$の集合論的定義

\mathbb {T} =SO(2) =U(1) =S^1 =\{z\in \mathbb {C} :|z|=1\}

• 上掲の同型群の角θによる媒介変数表示(指数写像)

\theta \mapsto z=e^{i\theta }=\cos \theta +i\sin \theta

円周群 -Wikipedia

円周群$\mathbb{T}$の回転群SO(n)としての解釈は、標準位相に関して円周群が一次元トーラスに位相群として同型であるという事実に発する。より一般に円周群$\mathbb{T}$のn重直積群$\mathbb{T}^n$は幾何学的にn次元トーラスとなる。

そんな感じで以下続報…