【Python演算処理】環論(Ring Theory)に立脚した全体像再構築①空環(Empty Ring)と実数環(Real Ring)

群論(Group Theory)の導入は自明の場合(Trival Case)として環論(Ring Theory)への拡張を伴います。まぁまずいきなりその全貌なんて理解出来ません。
環論 - Wikipedia
それでは何を掴んだのか。まずはその再確認から始めたいと思います。

#空環概念(Empty Ring Concept)の再構築

空環(Empty Ring)$\emptyset _n(n=0)=()$とは「空和概念(Empty Sum Concept)」と「空積概念(Empty Product Concept)」の統合結果です。

###空積概念(Empty/Nullary Product Concept)

import networkx as nx

G = nx.DiGraph()
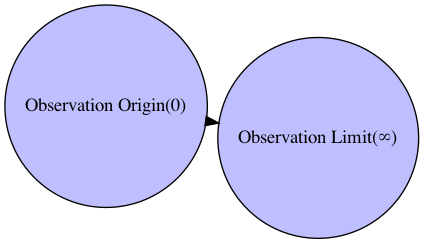
G.add_edge("Observation Origin(0)","Observation Limit(∞)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

• 観測限界(Observation Limit)∞も観測原点(Observation Origin)0も点と置いた場合、この2点を結ぶ距離$x$(範囲0~∞)は、何倍にしても何分の1にしても結果は観測限界∞のままである。
• ただし例外的に$\frac{x}{x}=1$となり、これが乗法単位元(Multiplicative
  Identity)と乗法群（Multiplicative Group)の概念の出発点になる。

###空和概念(Empty/Nullary Sum Concept)

import networkx as nx

G = nx.DiGraph()
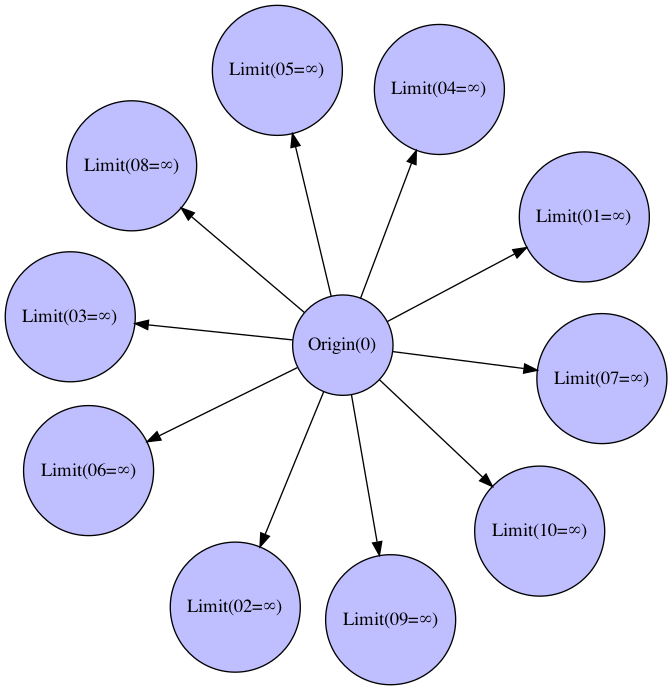
G.add_edge("Origin(0)","Limit(01=∞)")
G.add_edge("Origin(0)","Limit(02=∞)")
G.add_edge("Origin(0)","Limit(03=∞)")
G.add_edge("Origin(0)","Limit(04=∞)")
G.add_edge("Origin(0)","Limit(05=∞)")
G.add_edge("Origin(0)","Limit(06=∞)")
G.add_edge("Origin(0)","Limit(07=∞)")
G.add_edge("Origin(0)","Limit(08=∞)")
G.add_edge("Origin(0)","Limit(09=∞)")
G.add_edge("Origin(0)","Limit(10=∞)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

• 観測限界∞を観測原点０との距離$x$(範囲0~∞)を半径とする円弧/球面と置いた場合、それをどんな数を加減しても結果は観測限界∞のままである。
• ただし例外的に$x-x=0$となり、これが加法単位元(Additive Identity Identity)と加法群(Additive Group)の概念の出発点になる。

そして空和の指数写像(Exponential Map)が空積、空積の対数写像(Logarithmic Map)が空和となり、これが環(Ring)概念の出発点となるのです。

(\emptyset,+) \cong (\emptyset,×)

	空和(水平軸)	その指数写像としての空積(垂直軸)
0	0(半径0)	0(半径0)
1	1(半径1)　*空集合なので未検出	1(半径1)　*空集合なので未検出
2	∞(半径π)	2(半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["0(半径0)","1(半径1)　*空集合なので未検出","∞(半径π)"],
    ["0(半径0)","1(半径1)　*空集合なので未検出","2(半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['空和(水平軸)', 'その指数写像としての空積(垂直軸)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="olivedrab",lw=0.5)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([0,np.pi*2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map100001.gif", writer="pillow")

	空積(垂直軸)	その対数写像としての空和(水平軸)
0	0(半径0)	0(半径0)
1	1(半径1)　*空集合なので未検出	1(半径1)　*空集合なので未検出
2	2(半径0)	∞(半径π)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["0(半径0)","1(半径1) *空集合なので未検出","2(半径0)"],
    ["0(半径0)","1(半径1) *空集合なので未検出","∞(半径π)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['空積(垂直軸)', 'その対数写像としての空和(水平軸)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="olivedrab",lw=0.5)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([0,np.pi*2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]
Time_Code.reverse()

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map200001.gif", writer="pillow")

①要するに空環の段階においてオイラーの等式$e^{πi}=-1$は既に成立しているものと考える。それが「乗法群としての空積概念と加法群としての空和概念を指数/対数写像によって統合する」空環概念の成立条件なのである。

②同時にこの段階において既に(それ自体は観測不可能な)観測原点0と観測限界∞の距離xの直径(Diameter)2への写像なる概念が現れている事から、以下の考え方も(実数の概念が成立した時点で)自明の場合(Trival Case)として成立するものと考える。

• 2の冪乗算$f(x)=2^x$と「0から2までの正の実数」の組み合わせによって(それ自体は観測不能な観測原点0と観測限界∞の間の開集合として)任意の正の実数およびその指数写像を表せる。

\mathbb{R}^{+}=(2^n+x|n \in \mathbb{Z}^{+},x \in \mathbb{R} \land 0  \leqq x  \leqq 2)

	Values	Explessions
1	1	2^0
2	2	2^1
3	3	2^0+2^1 / 2^log(3,base=2)
4	4	2^2
5	5	2^2+2^0
6	6	2^2+2^1
7	7	2^2+2^log(3,base=2)
8	8	2^3

• その対数写像、すなわち「0から2までの正の実数」と$\log2$の概念を組み合わせによって(それ自体は観測不能な観測原点0と観測限界∞の間の開集合として)任意の正の対数を表せる。

\log(\mathbb{R}^{+})=(\log_2^n+x|n \in \mathbb{Z}^{+} ,x \in \mathbb{R} \land 0 \leqq x \leqq 2)

	Numbers	Explessions	Values
1	log(1)	log(2^1)+log(1/2)	0
2	log(2)	log(2^1)	0.6931472
3	log(3)	log(3/2)+log(2^1)	1.098612
4	log(4)	log(2^2)	1.386294
5	log(5)	log(5/4)+log(2^2)	1.609438
6	log(6)	log(3/2)+log(2^2)	1.791759
7	log(7)	log(7/4)+log(2^2)	1.94591
8	log(8)	log(2^3)	2.079442

#実数環概念(Real Ring Concept)の再構築

上掲の「正の実数」概念から出発します。

###加法実数群(Additive Real Group)概念の設定

以下の定義によってとりあえず実数列(Real Sequence)$\mathbb{R}$全域が表せる様になります。ただしこの段階で可能な演算はスカラー倍(その逆数をとればスカラー割)と加減算のみ。線形代数(linear Algebra)の表現を用いるなら「既にベクトル空間(Vector Space)としては成立しているが、まだ計量ベクトル空間(Metric Vector Space)には至ってない」段階となります。
群の定義といろいろな具体例 | 高校数学の美しい物語

①まず加法単位元(Additive Identity)0の概念を追加した集合Aを準備する。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(0,2,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[0,2],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([rollx,rollx],[rolly,rolly],[0,2],color="blue",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([0,rollx],[0,rolly],[2,2],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([0.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=45, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1]
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder001.gif", writer="pillow")

②集合Aに対する逆元(Inverse Element)$A^{−1}$を準備する。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-2,0,1201,endpoint = True)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-2,61)
uz1=num.repeat(-1,61)
uz2=num.repeat(0,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[0,-2],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([rollx,rollx],[rolly,rolly],[0,-2],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[-2,-2],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-2.1,0.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=45, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder002.gif", writer="pillow")

③両者を統合する。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=45, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder003.gif", writer="pillow")

###乗法実数群(Multiplicative Real Group)概念の追加

既に説明した様に、環へと拡張したければ加法実数群の指数/対数写像を考えれば良い訳です。

• 指数写像(Exponential Map)

	加法実数群	乗法実数群
0	-∞	0
1	-1	exp(-1)
2	0	1
3	1	exp(+1)
4	+∞	∞

import numpy as np
import pandas as pd
X1 = np.matrix([
    ["-∞","-1","0","1","+∞"],
    ["0","exp(-1)","1","exp(+1)","∞"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['加法実数群', '乗法実数群'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

• 対数写像(Logarithmic Map)

	乗法実数群	加法実数群
0	0	-∞
1	exp(-1)	-1
2	1	0
3	exp(+1)	1
4	∞	+∞

import numpy as np
import pandas as pd
X1 = np.matrix([
    ["0","exp(-1)","1","exp(+1)","∞"],
    ["-∞","-1","0","1","+∞"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['乗法実数群', '加法実数群'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

• この操作によって加法実数群における乗除算は乗法実数群における加減算に、加法実数群における冪算は乗法実数群における乗算に対応付けられる。
  【数理考古学】常用対数表を使った計算

(\mathbb {R},+) \cong (\mathbb{R}^{+},×)

かかる全体像を「縦軸(高さz)に均等尺(Even Scale)、横軸(半径r)に対数尺(Logarithmic Scale)を採用した円筒座標系(Cylindrical Coordinate System)」とイメージすると、とりあえず半径$r=e^0=1$の場合が実数列(加法実数群)に一致します。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱高計算
    h1=2*n/len(uc)-1
    hz=np.repeat(h1,len(uc))
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #移動円追加
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[h1,h1],color="purple",lw=0.5)
    ax.plot(uc.real,uc.imag,hz,color="purple",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,h1],color="purple",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=25,0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=25, azim=-45)

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Tcode))
ani.save("cylinder402.gif", writer="pillow")

傾きの分母が常に単位円の半径1となるからですね。

import sympy as sp
import numpy as np
from sympy import I, pi, E
x,y,z,r,φ,m,S,V= sp.symbols('x,y,z,r,φ,m,S,V')

#sp.Eq(z,z)と書いてもTrueという
#論理演算結果が返るのみなので省略

#デカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
eq01=sp.Eq(r,sp.sqrt(x**2+y**2))
eq02=sp.Eq(φ,sp.sign(y)*sp.atan2(y,x))
eq03=sp.Eq(x,r*sp.cos(φ))
eq04=sp.Eq(y,r*sp.sin(φ))
eq05=sp.Eq(m,sp.tan(φ))
eq06=sp.Eq(m,z/r)
eq07=sp.Eq(S,2*pi*r**2+2*pi*r*z)
eq08=sp.Eq(V,pi*r**2*z)

#単位円(半径r=1)の場合
eq11=eq01.subs(r,1)
eq12=eq02.subs(r,1)
eq13=eq03.subs(r,1)
eq14=eq04.subs(r,1)
eq15=eq05.subs(r,1)
eq16=eq06.subs(r,1)
eq17=eq07.subs(r,1)
eq18=eq08.subs(r,1)

#tex
sp.init_printing()
print("デカルト座標系(x,y,z)と極座標系(r,φ,z)の相互変換")
display(eq01)
print(sp.latex(eq01))
display(eq02)
print(sp.latex(eq02))
display(eq03)
print(sp.latex(eq03))
display(eq04)
print(sp.latex(eq04))
display(eq05)
print(sp.latex(eq05))
display(eq06)
print(sp.latex(eq06))
display(eq07)
print(sp.latex(eq07))
display(eq08)
print(sp.latex(eq08))
print("単位円(半径r=1)の場合")
display(eq11)
print(sp.latex(eq11))
display(eq12)
print(sp.latex(eq12))
display(eq13)
print(sp.latex(eq13))
display(eq14)
print(sp.latex(eq14))
display(eq15)
print(sp.latex(eq15))
display(eq16)
print(sp.latex(eq16))
display(eq17)
print(sp.latex(eq17))
display(eq18)
print(sp.latex(eq18))

デカルト座標系(x,y,z)と極座標系(r,φ,z)の相互変換

\begin{align*}
&r = \sqrt{x^{2} + y^{2}}\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&x = r \cos{\left(φ \right)}\\
&y = r \sin{\left(φ \right)}\\
&z = z\\
&傾きm = \tan{\left(φ \right)}\\
&傾きm = \frac{z}{r}\\
&表面積S = 2 \pi r^{2} + 2 \pi r z\\
&体積V = \pi r^{2} z
\end{align*}

単位円(半径r=1)の場合(実数列$\mathbb{R}$そのものとなる)。

\begin{align*}
&r = 1\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&x = \cos{\left(φ \right)}\\
&y = \sin{\left(φ \right)}\\
&z = z\\
&傾きm = \tan{\left(φ \right)}\\
&傾きm = z\\
&表面積S = 2 \pi z + 2 \pi\\
&体積V = \pi z
\end{align*}

それではこのイメージの同心円的拡張を考えてみましょう。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱高計算
    h1=2*n/len(uc)-1
    hz=np.repeat(h1,len(uc))
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #半円柱描画
    ax.plot(s1.real/2,s1.imag/2,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #半単位円描画
    ax.plot(uc.real/2,uc.imag/2,uz0,color="red",lw=1)
    ax.plot(uc.real/2,uc.imag/2,uz1,color="green",lw=1)
    ax.plot(uc.real/2,uc.imag/2,uz2,color="blue",lw=1)    
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #半実数線追加
    ax.plot([1/2,1/2],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1/2,1/2],[0,0],[0,1],color="blue",lw=1)
    #移動円追加
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[h1,h1],color="purple",lw=0.5)
    ax.plot(uc.real,uc.imag,hz,color="purple",lw=1)
    ax.plot(uc.real/2,uc.imag/2,hz,color="purple",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,h1],color="purple",lw=1)
    ax.plot([0,uc[n].real*1/2],[0,uc[n].imag*1/2],[0,h1],color="purple",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=25,0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=25, azim=-45)

Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder501.gif", writer="pillow")

2つの同心円の関係は$2^{-1}=\frac{1}{2}:2^{0}=1$とも$2^{0}=1:2^1=2$とも取れます。要するにとりあえずこのプログラムで図示した同心集合(Concentric Set)は演算$2^n(n \in \mathbb{Z})$の結果集合です。

2^n(n=-\infty→0→+\infty)=(2^{-\infty}=\frac{1}{\infty}=0,…,2^{-2}=\frac{1}{2^2}=\frac{1}{4},2^{-1}=\frac{1}{2^1}=\frac{1}{2},2^{0}=\frac{2^1}{2^1}=1,2^1=1,2^2=4,…,2^{+\infty}=\infty)

import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline

#単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)

#描画準備
fig = plt.figure()
ax = plt.axes()

def circle_draw(n):
    plt.cla()
    plt.title("Concentric Circles")
    plt.xlabel("X")
    plt.ylabel("Y")
    plt.ylim([-4.0,4.0])
    plt.xlim([-4.0,4.0])
    # 同心円描画
    plt.plot(0,0,marker='x', color='green')
    circle1=patches.Circle((0,0),radius=1/4, fill=True, color='gray',lw=0.5,alpha=0.5)
    circle2=patches.Circle((0,0),radius=1/2, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle3=patches.Circle((0,0),radius=1, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle4=patches.Circle((0,0),radius=2, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle5=patches.Circle((0,0),radius=4, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)    
    ax.add_patch(circle1)
    ax.add_patch(circle2)
    ax.add_patch(circle3)
    ax.add_patch(circle4)
    ax.add_patch(circle5)
    ax.add_patch(circle6)
    ax.set_aspect('equal', adjustable='box')
    #補助線描画
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    #移動線描画
    plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
    plt.plot(s1[n].real,s1[n].imag,marker='x', color='green')
    plt.plot(s1[n].real*1/4,s1[n].imag*1/4,marker='x', color='green')
    plt.plot(s1[n].real*1/2,s1[n].imag*1/2,marker='x', color='green')
    plt.plot(s1[n].real*1,s1[n].imag*1,marker='x', color='green')
    plt.plot(s1[n].real*2,s1[n].imag*2,marker='x', color='green')
    plt.plot(s1[n].real*4,s1[n].imag*4,marker='x', color='green')
#circle_draw(1)
#plt.show()

ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw60003.gif", writer="pillow")

ところで全ての指数関数(Exponential Function)$a^n$は以下の変換式を用いて自然指数関数(Natural Exponential Function)$e^n$へと変換可能ですから、この比例関係は自然指数関数の部分集合であると一般化され、実数環成立の条件が満たされるのです。

a^n=e^{n\log{a}}\\
2^n=e^{n\log{2}}\\
\log{2}=0.6931472

import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline

#単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
    s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)

#描画準備
fig = plt.figure()
ax = plt.axes()

def circle_draw(n):
    plt.cla()
    plt.title("Concentric Circles")
    plt.xlabel("X")
    plt.ylabel("Y")
    plt.ylim([-4.0,4.0])
    plt.xlim([-4.0,4.0])
    # 同心円描画
    plt.plot(0,0,marker='x', color='green')
    circle1=patches.Circle((0,0),radius=np.exp(-2), fill=True, color='gray',lw=0.5,alpha=0.5)
    circle2=patches.Circle((0,0),radius=np.exp(-1), fill=True, color='gray',lw=0.5,alpha=0.2)
    circle3=patches.Circle((0,0),radius=np.exp(0), fill=True, color='gray',lw=0.5,alpha=0.2)
    circle4=patches.Circle((0,0),radius=np.exp(1), fill=True, color='gray',lw=0.5,alpha=0.2)
    circle5=patches.Circle((0,0),radius=np.exp(2), fill=True, color='gray',lw=0.5,alpha=0.2)
    circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)    
    ax.add_patch(circle1)
    ax.add_patch(circle2)
    ax.add_patch(circle3)
    ax.add_patch(circle4)
    ax.add_patch(circle5)
    ax.add_patch(circle6)
    ax.set_aspect('equal', adjustable='box')
    #補助線描画
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    #移動線描画
    plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
    plt.plot(s1[n].real,s1[n].imag,marker='x', color='green')
    plt.plot(s1[n].real*np.exp(-2),s1[n].imag*np.exp(-2),marker='x', color='green')
    plt.plot(s1[n].real*np.exp(-1),s1[n].imag*np.exp(-1),marker='x', color='green')
    plt.plot(s1[n].real*np.exp(0),s1[n].imag*np.exp(0),marker='x', color='green')
    plt.plot(s1[n].real*np.exp(1),s1[n].imag*np.exp(1),marker='x', color='green')
    plt.plot(s1[n].real*np.exp(2),s1[n].imag*np.exp(2),marker='x', color='green')
#circle_draw(1)
#plt.show()

ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw60004.gif", writer="pillow")

こうした全体像を群論は以下の様に定義します。

群同型 Wikipedia

加法整数群$(\mathbb {Z},+)$は加法実数群$(\mathbb{R},+)$の部分群であり、商群$\frac{\mathbb{R}}{\mathbb{Z}}$は、同型写像$f(x+\mathbb {Z})=e^{2πxi}(x \in \mathbb{R} \land 0 \leqq x \leqq 2π)$によって絶対値1の乗法複素数群$S^1$に同型である：

\frac{(\mathbb{R},+)}{(\mathbb{Z},+)} \cong S^1

半径$e^0=1$の場合についてしか語っていない、すなわち写像として演算$f(x)=e^{xi}(x \in \mathbb{R} \land 0 \leqq x \leqq 2π)$の結果集合しか想定してない様にも見えますが、まぁそれはそれ。

e^{2πi}(exp(0+6.283185i))=\cos(2π)+\sin(2π)i=1+0i\\
e^{πi}(exp(0+3.141593i))=\cos(π)+\sin(π)i=-1+0i\\
-e^{πi}(-exp(0+3.141593i))=-\cos(π)-\sin(π)i=1+0i

また

-1^n=±i^{2n}\\
-1^1=±i^{2}=-1\\
-1^2=±i^{2*2}=1

とにかくこの時点において初めて整数列(Integer Sequence)概念が「周回数(Rap)」として導入される展開を迎える訳ですが、ここで周期(Circle)を2と取るか1と取るかでそれを扱う演算の構成が全く変わってしまう訳です。

#周期2の場合…偶数群(Even Group)と奇数集合(Odd Set)の交代的出現
以下の演算の結果集合です。

{-1^n(n=-\infty→+\infty)=(-1,…,1,-1,1,…,-1)
}

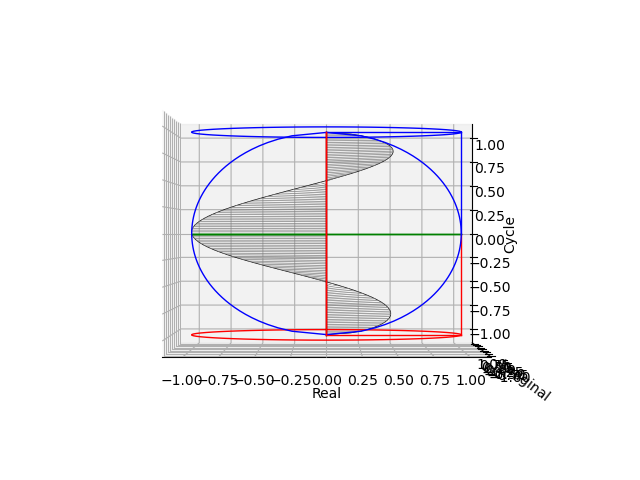
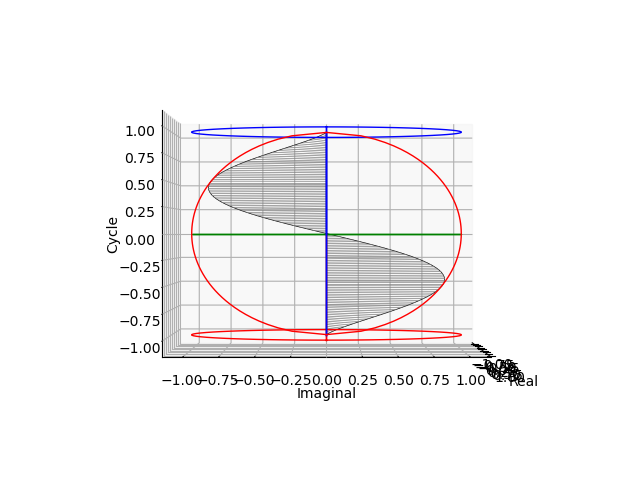
その水平位置からの観測結果(周期2のcos(θ)cos⁡(θ)波とsin(θ)sin⁡(θ)波の検出)

cos(θ)波

sin(θ)波

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*2,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,121,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱とスポークの描画
    s2=[]
    for nm in range(len(c0)):
        s2.append(complex(m.cos(c0[nm]+Tcode[n]),m.sin(c0[nm]+Tcode[n])))
    s3=np.array(s2)
    ax.plot(s3.real,s3.imag,z0,color="black",lw=0.5)
    for nm in range(len(s3)):
        ax.plot([0,s3[nm].real],[0,s3[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([-1,1],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([-1,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([-1,1],[0,0],[1,1],color="black",lw=1)
    ax.plot([1,1],[0,0],[-1,1],color="black",lw=1)
    ax.plot([-1,-1],[0,0],[-1,1],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,-rollx],[0,-rolly],[0,0],color="green",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("uc003.gif", writer="pillow")

球面展開では以下となりますね。上面図が「回るケツの割れ目」…



$\sin(θ)\cos(θ)$波の検出

• 0/2πラジアンの時0
• ±$\frac{π}{2}$ラジアンの時$\frac{1}{2}$
• πラジアンの時-1

$\sin(θ)\sin(θ)$波の検出

• 0/2π/±$\frac{π}{2}$ラジアンの時0
• 半径±$\frac{1}{2}$の時に頂点

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円球データ準備
def src(x):
    return m.sqrt(1-x**2)
c0=num.linspace(0,m.pi*2,121,endpoint = True)
zc=num.linspace(-1,1,121,endpoint = True)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiBH=num.linspace(-1,1,61,endpoint = True)
MiBd=num.sqrt(1-MiBH**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円球とスポークの描画
    s0=[]
    for nm in range(len(c0)):
        s0.append(complex(m.cos(c0[nm]+Tcode[n])*src(zc[nm]),m.sin(c0[nm]+Tcode[n])*src(zc[nm])))
    s1=num.array(s0)
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,-1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #球面描画
    roll0=[]
    for nm in range(len(MiBd)):
        roll0.append(c.rect(MiBd[nm],Tcode[n]))
    roll=num.array(roll0)
    ax.plot(roll.real,roll.imag,MiHz,color="blue",lw=1)
    ax.plot(-roll.real,-roll.imag,MiHz,color="blue",lw=1)
    ax.plot(roll.imag,-roll.real,MiHz,color="red",lw=1)
    ax.plot(-roll.imag,roll.real,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cuberoll101.gif", writer="pillow")

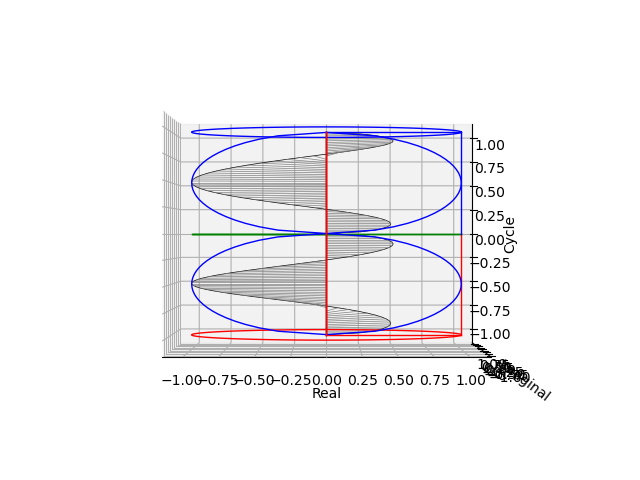
これまで扱ってきた単位円(Unit Circle)/単位球面(Unit Sphere)の直径(Diameter)が2である事に注目した結果、自明の場合として(1単位で増減する整数列を部分集合として含む)実数列は偶数群(Even Group)2nと奇数集合(Odd Set)2n+1の交代的出現によって説明される展開を迎えます。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

###偶数群(Even Group)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項0、公差±2、一般項±2nの両側無限数列を構成する。

Even_n(n=-\infty→0→+\infty)=(-\infty,…,-2n,…,-2×2=-4,-2×1=-2,-2×0=0,-2×1=2,-2×2=4,…,2n,…,+\infty)

• その演算は加減算の範囲で閉じており(偶数+偶数=偶数、偶数-偶数=偶数)、加法単位元と逆元を備え、かつ結合則(a+b)+c=a+(b+c)を満たす(元と単位元と逆元が同じ等差数列上に連続する)ので群の成立条件を満たす。

実際に確かめてみましょう。

①とりあえず-1から1にかけての方向で演算を確かめてみる。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real-1,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz-1,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([-np.pi,np.pi])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map400001.gif", writer="pillow")

②逆に1から-1にかけての方向で演算を試みた結果と重なる。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,Ed.real+1,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz+1,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="green",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([-np.pi,np.pi])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map500001.gif", writer="pillow")

「偶関数に逆関数は存在しない」とは、要するにこの様に「演算結果集合の元がぴったりと重なり合う=全単射条件が満たされる=群同型と見做される」事を指していたのです。さらに指数関数と三角関数はあらゆる角度からの演算がこの条件を満たす事で知られています。
【Python演算】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」？

• $Cos(θ)\frac{d^n}{dx^θ}=(-Sin(θ),-Cos(θ),Sin(θ),Cos(θ),…)$

• $Sin(θ)\frac{d^n}{dx^θ}=(Cos(θ),-Sin(θ),-Cos(θ),Sin(θ),…)$

• $\int \int \int … \int Cos(θ)(dθ)=(Sin(θ),-Cos(θ),-Sin(θ),Cos(θ),…)$

• $\int \int \int … \int Sin(θ)(dθ)=(Cos(θ),-Sin(θ),Cos(θ),Sin(θ),…)$

• $e^{ix}\frac{d^n}{dx^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$

• $\int \int \int … \int e^{ix}(dx)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$

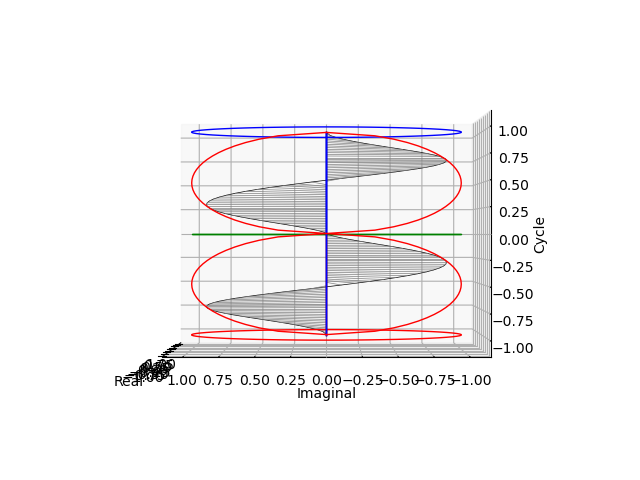
###奇数集合(Odd Set)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項1、公差±2、一般項±2n+1の両側無限数列を構成する。

Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n+1,…,-2×2+1=-3,-2×1+1=-1,2×0+1=1,2×1+1=3,…,2n+1,…,+\infty)

あるいは

Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n-1,…,-2×2-1=-5,-2×1-1=-3,2×0-1=-1,2×1-1=1,2×2-1=3,…,2n+1,…,+\infty)

• その演算は逆元を備え、結合則(a+b)+c=a+(b+c)も満たすものの、加法単位元0は集合範囲外で演算結果も閉じてない(奇数+奇数=偶数、奇数-奇数=偶数)。ゆえに群の成立条件を満たさない。
• 関数における奇関数も(その対称性ゆえにそれを備えない偶関数と異なり)逆関数を備え常に一対で現れる。また幾何学における(対蹠間を結ぶ直線が引けない)奇数角形の多角形もまた(それぞれ片側の対蹠にのみ接する)一対として現れる。この様に「偶数の対称性」と「奇数の双極性」の対比は(それぞれ形を変えながら)あらゆる分野に普遍的に現れる。

こちらも実際に試してみましょう。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real,color="gray",lw=0.5)
        ax.plot(rollxy.real,rollxy.imag,Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    ax.plot(rollc.real,rollc.imag,-rollz,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,-uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,-uz2,color="red",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="blue",lw=0.5)
        ax.plot([0,uc[num].real],[0,uc[num].imag],[-1,-1],color="red",lw=0.5)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,-2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([-np.pi,np.pi])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map300001.gif", writer="pillow")

今度は演算結果集合が全く重なりません。なるほど「逆関数が存在する」とはこういう状態を指していたのです。ただしここで偶奇性(Parity)が現れるのはあくまでZ軸においてであり(x軸線上やy軸線上における現れ方はあくまで偶関数)、これをx軸やy軸に置換して回転させるとトーラス座標系(Torus Coordinate System)の登場とあいなる訳です。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)

#小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])

#小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
    MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0) 

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#描画関数定義
def unit_cylinder(n):
    plt.cla()
    #断面計算
    MiAvD0=[]
    for nm in range(len(MiAvC)):
        MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
    MiAvD=num.array(MiAvD0) 
    MiBvD0=[]
    for nm in range(len(MiBx)):
        MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
    MiBvD=num.array(MiBvD0)
    MiCvD0=[]
    for nm in range(len(MiHz)):
        MiCvD0.append(c.rect(2,Tcode[n]))
    MiCvD=num.array(MiCvD0)
    #軌跡計算
    Orb_r=abs(MiAvD[n])
    Orb0=[]
    for nm in range(len(MiCvD)):
        Orb0.append(c.rect(Orb_r,Tcode[nm]))
    Orbv=num.array(Orb0)
    Orbh=num.repeat(MiAh[n],61)
    #断面1計算
    MiAvD10=[]
    for nm in range(len(MiAvC)):
        MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
    MiAvD1=num.array(MiAvD10) 
    MiBvD10=[]
    for nm in range(len(MiBx)):
        MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
    MiBvD1=num.array(MiBvD10)
    MiCvD10=[]
    for nm in range(len(MiHz)):
        MiCvD10.append(c.rect(2,Tcode[0]))
    MiCvD1=num.array(MiCvD10)  
    #円柱描画
    ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
    ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    #中心線描画
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #分割原点
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
    ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
    ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)    
    ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
    ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
    ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
    ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
    ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
    #アニメーション描画
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
    ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
    ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)    
    ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="red",lw=1)
    ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
    ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
    ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
    ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
    #軌跡描画
    ax.plot(Orbv.real,Orbv.imag,Orbh,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-2.1,2.1])
    ax.set_xlim([-2.1,2.1])
    ax.set_zlim([-2.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=25, azim=45)

Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
#Time_code0=num.arange(0,360,6) 
#Time_code=Time_code0[::-1] 
#unit_cylinder(15)
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output620.gif", writer="pillow")

【Python演算処理】単位球面を巡る数理②そして単位トーラスへ

大半径(Major Radius)Rと小半径(Minor Radius)の組み合わせで表現されるトーラス座標系(Torus Coordinates System)とデカルト座標系の関係は、一般に媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表されます。

• x=$R×\cos(t)+r×\cos(p)\cos(t)$
• y=$R×cos(t)+r×\cos(p)\sin(t)$
• z=$r×\sin(p)$
• 表面積$S=4π^2rR=(2πr)(2πR)$
• 体積$V=2π^2r^2R=(πr^2)(2πR)$

上掲の円/球面座標系との関係は以下となります。

• 大半径R=0,小半径r=1の時、単位球面(Unit Sphere)を二重に描く。従って経緯度法(経度-180度→+180度に対して緯度-90度→+90度)や3次元極座標系(水平角φ=-π→+πに対して垂直角θ=0→π)は適用範囲を半分に減らしてなお単位球面(Unit Sphere)上の全座標を示せる訳である。
• 逆に大半径R=1,小半径r=0の時、Z=0となってただの単位円(Unit Circle)となる。大半径Rと小半径rの比が1:1の場合(外径が半径1の単位円と一致するのは大半径R=小半径r=$\frac{1}{2}$の時で、大半径R=小半径r=1の時の外径は2となる）からこの極限状態に向かう展開は「半径1の単位円に内接する正N角形とそのさらなる内接円の推移($N=\infty$に近づくほど、その正N角形の辺長計は円周長2πに限りなく近づく)」数理そのものである。
  【初心者向け】挟み撃ち定理による円周率πの近似
  

import sympy as sp
import numpy as np
from sympy import I, pi, E
x,y,z,r,R,p,t,S,V= sp.symbols('x,y,z,R,r,p,t,S,V')

#トーラス座標系(R,t)(r,p)からデカルト座標系(x,y,z)への変換
eq01=sp.Eq(x,R*sp.cos(t)+r*sp.cos(p)*sp.cos(t))
eq02=sp.Eq(y,R*sp.sin(t)+r*sp.cos(p)*sp.sin(t))
eq03=sp.Eq(z,r*sp.sin(p))
eq04=sp.Eq(S,4*pi**2*r*R)
eq05=sp.Eq(S,(2*pi*r)*(2*pi*R))
eq06=sp.Eq(V,2*pi**2*r**2*R)
eq07=sp.Eq(V,(pi*r**2)*(2*pi*R))

#大半径R=0,小半径r=1の時
eq11=eq01.subs([(r,1),(R,0)])
eq12=eq02.subs([(r,1),(R,0)])
eq13=eq03.subs([(r,1),(R,0)])
eq14=eq04.subs([(r,1),(R,0)])
eq15=eq05.subs([(r,1),(R,0)])
eq16=eq06.subs([(r,1),(R,0)])
eq17=eq07.subs([(r,1),(R,0)])

#大半径R=1,小半径r=0の時
eq21=eq01.subs([(r,0),(R,1)])
eq22=eq02.subs([(r,0),(R,1)])
eq23=eq03.subs([(r,0),(R,1)])
eq24=eq04.subs([(r,0),(R,1)])
eq25=eq05.subs([(r,0),(R,1)])
eq26=eq06.subs([(r,0),(R,1)])
eq27=eq07.subs([(r,0),(R,1)])

#大半径R=1,小半径r=1の時
eq31=eq01.subs([(r,1),(R,1)])
eq32=eq02.subs([(r,1),(R,1)])
eq33=eq03.subs([(r,1),(R,1)])
eq34=eq04.subs([(r,1),(R,1)])
eq35=eq05.subs([(r,1),(R,1)])
eq36=eq06.subs([(r,1),(R,1)])
eq37=eq07.subs([(r,1),(R,1)])

#tex
sp.init_printing()
print("トーラス座標系(R,t)(r,p)からデカルト座標系(x,y,z)への変換")
display(eq01)
print(sp.latex(eq01))
display(eq02)
print(sp.latex(eq02))
display(eq03)
print(sp.latex(eq03))
display(eq04)
print(sp.latex(eq04))
display(eq05)
print(sp.latex(eq05))
display(eq06)
print(sp.latex(eq06))
display(eq07)
print(sp.latex(eq07))
print("大半径R=0,小半径r=1の時")
display(eq11)
print(sp.latex(eq11))
display(eq12)
print(sp.latex(eq12))
display(eq13)
print(sp.latex(eq13))
display(eq14)
print(sp.latex(eq14))
display(eq15)
print(sp.latex(eq15))
display(eq16)
print(sp.latex(eq16))
display(eq17)
print(sp.latex(eq17))
print("大半径R=1,小半径r=0の時")
display(eq21)
print(sp.latex(eq21))
display(eq22)
print(sp.latex(eq22))
display(eq23)
print(sp.latex(eq23))
display(eq24)
print(sp.latex(eq24))
display(eq25)
print(sp.latex(eq25))
display(eq26)
print(sp.latex(eq26))
display(eq27)
print(sp.latex(eq27))
print("大半径R=1,小半径r=1の時")
display(eq31)
print(sp.latex(eq31))
display(eq32)
print(sp.latex(eq32))
display(eq33)
print(sp.latex(eq33))
display(eq34)
print(sp.latex(eq34))
display(eq35)
print(sp.latex(eq35))
display(eq36)
print(sp.latex(eq36))
display(eq37)
print(sp.latex(eq37))

トーラス座標系(R,t)(r,p)からデカルト座標系(x,y,z)への変換

\begin{align*}
&x = R \cos{\left(p \right)} \cos{\left(t \right)} + r \cos{\left(t \right)}\\
&y = R \sin{\left(t \right)} \cos{\left(p \right)} + r \sin{\left(t \right)}\\
&z = R \sin{\left(p \right)}\\
&S = 4 \pi^{2} R r\\
&V = 2 \pi^{2} R^{2} r
\end{align*}

大半径R=0,小半径r=1の場合

\begin{align*}
&x = \cos{\left(p \right)} \cos{\left(t \right)}\\
&y = \sin{\left(t \right)} \cos{\left(p \right)}\\
&z = \sin{\left(p \right)}
\end{align*}

• 大半径Rに直交する小半径rがらみの演算だけが残り、三次元極座標系r(φ,θ)を90度回転させた様な式に従う半径1の単位球面が現れる。rの範囲は2π（0~2πあるいは-π~π)なので三次元極座標系や緯度経度法の考え方を援用しても「２個分ある」。
• ちなみに2πR=0なので表面積も体積も0。rR比概念では到達不可能な極限状態の一つ。

大半径R=1,小半径r=0の場合

\begin{align*}
&x = \cos{\left(t \right)}\\
&y = \sin{\left(t \right)}\\
&z = 0
\end{align*}

• 大半径Rがらみの演算だけが残り、二次元極座標系r(φ)に従う半径1の単位円(高さ0)が現れる。
• やはり2πr=0なので表面積も体積も0。rR比概念では到達不可能な極限状態のもう一つ。

大半径R=1,小半径r=1の場合(単位トーラス)

\begin{align*}
&x = \cos{\left(p \right)} \cos{\left(t \right)} + \cos{\left(t \right)}\\
&y = \sin{\left(t \right)} \cos{\left(p \right)} + \sin{\left(t \right)}\\
&z = \sin{\left(p \right)}\\
&S = 2π*2π =4 \pi^{2}\\
&V = π*2π = 2 \pi^{2}
\end{align*}

トーラス Wikipedia

トーラスの表面積は底面が半径rで高さが2πRの円柱の側面積に等しく、体積はその円柱と同値となる。

すなわち上掲における赤い円弧の動きは「(コンピューターRPGの世界マップの様な)2π×2πの面積を有する平坦トーラス(Flat Torus)のどちらかの軸を二次元トーラスの大半径に射映すると、もう一方の軸上の移動が小半径上の回転(x軸上の0から2にかけての動き)に射映される」状況を表している訳です。
【Python画像処理】メルカトル図法と正距方位図法

そして自明の場合(Trival Case)としてこれら二次元トーラス座標系の集合は「半径πの球面と半径2の球面を指数/対数写像によって結びつけた全体像」の部分集合と規定され、そしてまさにこの瞬間「2乗すると円の面積πとなる数」$\sqrt{π}$の概念が導入される展開を迎えるのです。

• １辺が2∞(x=y=-∞→~+∞)の矩形の面積は$4∞^2(2∞^2-2∞^2)=∞(0)$で、その結果は半径∞の円の面積$π∞^2(\frac{π}{2}∞^2-\frac{π}{2}∞^2)=∞(0)$に一致する(ガウス分析における広義積分で計算領域を円から矩形に切り替えられる理由がこれ)
• 単位トーラス(大半径も小半径も1)の平面写像(Flat Map)、すなわち１辺が2π(x=y=-π→+π)の矩形の面積は$2^2π^2(2π^2-2π^2)=4π^2(0)$となる。
• ③②の計算結果を半径1(x=y=-1→+1)の単位円の面積$1^2π(\frac{π}{2}-\frac{π}{2})=π(0)$に射映すると(面積を一致させると)１辺が$\sqrt{π}(x=y=-\frac{\sqrt{π}}{2}→\frac{\sqrt{π}}{2})$の矩形が現れる。
• ④さらに③の矩形を(統計学上の確率計算において百分率=%表示に使う)辺長1、面積1の方眼(x=y=-1→1の第一象限)に射映すると(面積を一致させると)辺長$\frac{\sqrt{π}}{2}$の矩形が現れる。

そしてここで④の逆数$\frac{2}{\sqrt{π}}$を最大値を±1に取る単位ベルカーブ(Unit Bell Curve=単位Gaussian$±x^2$の指数写像)$y=exp^{±x^2}$を掛け合わせるとx=0の時の積分結果が1となる誤差関数(ERF=Error Function)が現れる訳です。
【Pyrhon演算処理】確率密度空間と累積分布空間②中心極限定理定理の可視化

y=(1 - \frac{x^2}{N})^N,-(1 - \frac{x^2}{N})^N

\operatorname {erf} \left(x\right)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t\\
\operatorname {erf}(∞)=1\\
\frac{d}{d x} \operatorname{erf}{\left(x \right)}=\frac{2 e^{- x^{2}}}{\sqrt{\pi}}

統計学の分野はこういう（平坦トーラス=コンピューターRPGにおける世界地図概念を介した）思わぬ形で群論とつながってくるのですね。

#周期1の場合…Γ関数(Gamma Function)の登場
以下の演算の結果集合です。

{1^n(n=-\infty→+\infty)=(1,…,1,1,1,…,1)
}

その水平位置からの観測結果(周期1のcos(θ)cos⁡(θ)波とsin(θ)sin⁡(θ)波の検出)

cos(θ)波

sin(θ)波

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*4,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,121,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱とスポークの描画
    s2=[]
    for nm in range(len(c0)):
        s2.append(complex(m.cos(c0[nm]+Tcode[n]),m.sin(c0[nm]+Tcode[n])))
    s3=np.array(s2)
    ax.plot(s3.real,s3.imag,z0,color="black",lw=0.5)
    for nm in range(len(s3)):
        ax.plot([0,s3[nm].real],[0,s3[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="black",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="black",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="green",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1] 
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("uc001.gif", writer="pillow")

球面展開では以下となります。「回るケツの割れ目」再び…



$\sin(θ)\cos(θ)$波の検出

• 0/2πラジアンの時0
• ±$\frac{π}{2}$ラジアンの時$\frac{1}{2}$
• πラジアンの時-1

$\sin(θ)\sin(θ)$波の検出

• 0/2π/±$\frac{π}{2}$ラジアンの時0
• 半径±$\frac{1}{2}$の時に頂点

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円球データ準備
def src(x):
    return m.sqrt(1-x**2)
c1=num.linspace(0,m.pi*2,60,endpoint = False)
c2=num.linspace(0,m.pi*2,61,endpoint = True)
c0=num.concatenate([c1, c2])
z0=num.linspace(-1,1,121,endpoint = True)
zc1=num.linspace(-1,1,60,endpoint = False)
zc2=num.linspace(-1,1,61,endpoint = True)
zc=num.concatenate([zc1,zc2])

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiBH1=num.linspace(-1,1,30,endpoint = False)
MiBH2=num.linspace(-1,1,31,endpoint = True)
MiBH=num.concatenate([MiBH1,MiBH2])
MiBd=num.sqrt(1-MiBH**2)
MiHy=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円球とスポークの描画
    s0=[]
    for nm in range(len(c0)):
        s0.append(complex(m.cos(c0[nm]+Tcode[n])*src(zc[nm]),m.sin(c0[nm]+Tcode[n])*src(zc[nm])))
    s1=num.array(s0)
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #球面描画
    roll0=[]
    for nm in range(len(MiBd)):
        roll0.append(c.rect(MiBd[nm],Tcode[n]))
    roll=num.array(roll0)
    ax.plot(roll.real,roll.imag,MiHz,color="blue",lw=1)
    ax.plot(-roll.real,-roll.imag,MiHz,color="blue",lw=1)
    ax.plot(roll.imag,-roll.real,MiHz,color="red",lw=1)
    ax.plot(-roll.imag,roll.real,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cuberoll001.gif", writer="pillow")

###Γ関数(Gamma Function)の登場
こう考えると(1単位で増減する整数列を部分集合として含む)実数列の増減が周期の増減と一致する代わり、交代数列が小数点下(丁度$\frac{1}{2}$の位置)に押し込まれ、それを扱うのにΓ関数(Gamma Function)の援用を必要とする様になる訳なんですね。

【Python演算処理】階乗と順列と組み合わせ

\begin{align*}
&Γ(1) = 1\\
&Γ(n+1) = n!(n \in \mathbb{N})\\
&Γ(z+1) = zΓ(z)(z \in \mathbb{C} \land z>0)\\
&Γ(\frac{1}{2}) = \sqrt{π}\\
&Γ(\frac{1}{2}+n) = \frac{(2n-1)!!}{2^n}\sqrt{π}(n \in \mathbb{N})\\
&Γ(\frac{1}{2}-n) = \frac{(-2)^n}{(2n-1)!!}\sqrt{π}(n \in \mathbb{N})
\end{align*}

• こうした話は最終的に「交頂級数(Alternating Series)とは何か？」という話題につながっていく。
  交項級数とは - コトバンク
  交項級数 - Wikipedia

この考え方ではむしろ(数直線が段階的に拡張されていく一般的イメージでは自明の理と置かれる)整数列(Integer Sequence)$\mathbb{Z}$とは何か、有理数列(Rational Sequence)$\mathbb{Q}$とは何か問われる形になるのが興味深いですね。そしてこれまでずっと堂々巡りを続けてきた「(半径1に対する直径)2とは何か?」なる疑問に一応の決着を付け、指数・対数写像の概念に無事バトンタッチ出来たのが最大の成果の一つとなりました。そんな感じで以下続報…