【数学溢れ話】【Token】確率密度空間と累積分布空間②中心極限定理の可視化

【Pyrhon演算処理】同心集合①乗法的同心集合とは？
【Pyrhon演算処理】同心集合②加法的同心集合とは？
【Pyrhon演算処理】同心集合③環概念と指数/対数写像概念の導入

上記投稿で確率した「同心環(Concentric Ring)」概念に統計学の世界で該当するのが「確率の等高線(Probability Contour Lines)」概念となります。
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

その比例尺度(Proportional Scale)概念はある種の(ベクトル空間、すなわち角度や内積の概念が存在しない)球面座標系であり、同心環の円筒座標系の各次元は確率密度空間の以下の次元に対応する形となります。

• 垂直軸(加法群=均等尺)の単位元0→平均(Mean)μ、すなわち確率変数(Random Variable=データのMin~Max)分布の中心位置の初期設定
• 水平軸(乗法群=対数尺)の単位元1→分散(Variance)$σ^2$すなわち確率密度(Probability Densty=0/0%~1/100%)分布の広がり具合の初期設定

確率変数は座標軸としてこそ+∞~-∞の範囲を扱いますが、データ出現率は平均を離れるほど急激に小さくなると考えられており、それを表したのが例えば中心極限定理（CLT=Central Limit Theorem）に立脚する正規分布(Normal Distribution)となります。
中心極限定理 - Wikipedia

#平均(Mean)と分散(Variance)の観測(Observation)
中心極限定理は大数の弱法則(WLLN=Weak Law of Large Numbers)の延長線上に現れました。
大数の法則 - Wikipedia
実際にプログラミングして確かめてみましょう。分散は「餌(中心点)に集るハエの群」の様なアニメーションで示され、その数を増やすほど中心点=平均の位置を明らかとするのです。

• 「平均(Mean)」表示

import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
fig = plt.figure()
ax = plt.axes()
N=1200 #ここを順次変えていく。

def circle_draw(n):
    plt.cla()
    a = random.normal(0,1,N)
    b = random.normal(0,1,N)
    plt.title("Concentric Circles")
    plt.ylim([-4.0,4.0])
    plt.xlim([-4.0,4.0])
    plt.scatter(a, b, s=20, c='k',alpha=0.4)
    # 同心円描画
    plt.plot(np.mean(a),np.mean(b),marker='x', color='green')
    circle1=patches.Circle((np.mean(a),np.mean(b)),radius=1, fill=True, color='gray',lw=0.5,alpha=0.5)
    circle2=patches.Circle((np.mean(a),np.mean(b)),radius=2, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle3=patches.Circle((np.mean(a),np.mean(b)),radius=3, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle4=patches.Circle((np.mean(a),np.mean(b)),radius=4, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle5=patches.Circle((np.mean(a),np.mean(b)),radius=5, fill=True, color='gray',lw=0.5,alpha=0.2)
    circle6=patches.Circle((np.mean(a),np.mean(b)),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)    
    ax.add_patch(circle1)
    ax.add_patch(circle2)
    ax.add_patch(circle3)
    ax.add_patch(circle4)
    ax.add_patch(circle5)
    ax.add_patch(circle6)
    ax.set_aspect('equal', adjustable='box')

#circle_draw(1)
#plt.show()

ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=10)
ani.save("circle_draw51200.gif", writer="pillow")
#ファイル名も順次変える。

• 「分散(variance)」表示

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#単位球面データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)
#「曲率」を計算
cv0=np.linspace(-1,1,1201,endpoint = True)
cv1=np.sqrt(1-cv0**2)
#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def D3_Normal_Distribution(n):
    plt.cla()
    #座標のランダム生成
    x=np.random.randn(smpl)
    y=np.random.randn(smpl)
    z=np.random.randn(smpl)
    #球面表示
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.1)
    #ランダム生成座表描画
    ax.scatter(x, y, z,color='blue')
    #諸元追加
    ax.set_ylim([-2,2])
    ax.set_xlim([-2,2])
    ax.set_zlim([-2,2])
    ax.set_title("3D Normal Distributio")
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_zlabel("z")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=90,azim=-45)

#サンプル数
smpl=1200
#繰り返し回数
Time_Code=np.repeat(1,8)

#D3_Normal_Distribution(1)
#plt.show()

ani = animation.FuncAnimation(fig, D3_Normal_Distribution, interval=100,frames=len(Time_Code))
ani.save("rnd1200c.gif", writer="pillow")

②N(サンプル数)を1から次第に増大させていく。
N=1の時の中心(平均)の推移

「分散(variance)」表示



N=2の時の中心(平均)の推移

「分散(variance)」表示



N=3の時の中心(平均)の推移

「分散(variance)」表示



N=5の時の中心(平均)の推移

「分散(variance)」表示



N=15の時の中心(平均)の推移

「分散(variance)」表示



N=30の時の中心(平均)の推移

「分散(variance)」表示



N=120の時の中心(平均)の推移

「分散(variance)」表示



N=300の時の中心(平均)の推移

「分散(variance)」表示



N=1200の時の中心(平均)の推移

「分散(variance)」表示

• 上掲データは全て見掛けに関わらず「中心と認定された位置からの偏差距離」なる線状=1次元状態の集合として構成されている。従ってその統計処理も一次元的内容となる。
  【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?
• 中心表示がまるでカメラの手ブレみたいだが(大数の弱法則に従って観測数が多くなるほど安定する)、実際統計学の基礎は天体観測データからの誤差除去の方法として構築されたのである。歴史のこの時点においては観測対象が単一かつ純粋に物理法則にのみ従う存在だったので観測数が増えれば増えるほど「中心(平均)は最終的に一つに収束する」「外れ値が除去しやすくなり、誤差も縮小に向かう」と考えたのは当然の帰結だった。
  【数理考古学】無限遠点(Infinity)としての正規分布と分散概念の歴史
  【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。
• 一方、見ての通りこうしたデータから分散概念を発想するのは極めて難しく、実際それが本格的に普及したのは20世紀に入ってからであった。Variance（バリアンス）なる用語自体ロナルド・フィッシャーが1918年に導入したものである。その前身として一応は19世紀後半まで遡る「平均への回帰」なる概念が存在した。
  平均への回帰 Wikipedia

#　分散(Dispersion)の計算式の秘密?
ここで発想を変えて「球表面上の一様分布」を考えてみます。ハエは羽を切り落とされて餌(半径1の球面)の表面を這い回る地虫の様な存在に変貌しました。
Python で一様分布の計算をする

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from scipy.stats import stats
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#単位球面データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)
#「曲率」を計算
cv0=np.linspace(-1,1,1201,endpoint = True)
cv1=np.sqrt(1-cv0**2)
#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def D3_Normal_Distribution(n):
    plt.cla()
    #座標のランダム生成
    v=np.random.rand(smpl)*np.pi*2
    h=np.random.rand(smpl)*np.pi*2
    x=np.sin(h)*np.cos(v)
    y=np.sin(h)*np.sin(v)
    z=np.cos(h)
    #球面表示
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.1)
    #ランダム生成座表描画
    ax.scatter(x, y, z,color='blue')
    #諸元追加
    ax.set_ylim([-2,2])
    ax.set_xlim([-2,2])
    ax.set_zlim([-2,2])
    ax.set_title("3D Normal Distributio")
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_zlabel("z")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45,azim=-45)

#サンプル数
smpl=50
#繰り返し回数
Time_Code=np.repeat(1,8)

#D3_Normal_Distribution(1)
#plt.show()

ani = animation.FuncAnimation(fig, D3_Normal_Distribution, interval=100,frames=len(Time_Code))
ani.save("cnd0004a.gif", writer="pillow")

Z軸のデータを放棄すると「球面状の一様分布を垂直から観察した結果集合」なる新たな分布を得ます。Z座標は式$z=\sqrt{1-x^2+y^2}$で復元可能ですが、そのままだと$Z \geqq 0(z>0)$半球と$Z<0(z\leqq 0)$半球のデータが区別出来ないので各データの符号だけは保存しておいて再利用しないといけません。しかし実は縦に割って符号以外放棄するのはy軸でも構わない訳です。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
fig = plt.figure()

#add_subplot()でグラフを描画する領域を追加する．引数は行，列，場所
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
#単位円データ作成
u0=np.linspace(0,np.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(np.cos(u0[nm]),np.sin(u0[nm])))
uc=np.array(u1)

#関数定義
def Riemann_sphere00(n):
    ax1.cla()
    ax2.cla()
    #座標のランダム生成
    v=np.random.rand(smpl)*np.pi*2
    h=np.random.rand(smpl)*np.pi*2
    x=np.sin(h)*np.cos(v)
    y=np.sin(h)*np.sin(v)
    z=np.cos(h)
    #Z軸振り分け
    mx0=[]
    my0=[]
    px0=[]
    py0=[]
    for nm in range(len(z)):
        if z[nm] >= 0:
            px0.append(x[nm])
            py0.append(y[nm])
        else:
            mx0.append(x[nm])
            my0.append(y[nm])
    mx=np.array(mx0)
    my=np.array(my0)
    px=np.array(px0)
    py=np.array(py0)
    c1,c2 = "blue","red" # 各プロットの色
    l1,l2 = "Minus","Plus" # 各ラベル
    #図(左上)描写
    ax1.plot(uc.real,uc.imag,color="black",lw=1)
    ax1.scatter(mx, my, color=c1, label=l1)
    ax1.set_xlim([-1.1,1.1])
    ax1.set_ylim([-1.1,1.1])
    #図(右上)描写
    ax2.plot(uc.real,uc.imag,color="black",lw=1)
    ax2.scatter(px, py, color=c2, label=l2)
    ax2.set_xlim([-1.1,1.1])
    ax2.set_ylim([-1.1,1.1])
    #諸元追加
    ax1.legend(loc = 'upper right') #凡例
    ax2.legend(loc = 'upper right') #凡例
    fig.tight_layout()              #レイアウトの設定

#サンプル数
smpl=50
#繰り返し回数
Time_Code=np.repeat(1,8)

#Riemann_sphere00(0)
#plt.show()

ani = animation.FuncAnimation(fig, Riemann_sphere00, interval=100,frames=len(Time_Code))
ani.save("RS0150.gif", writer="pillow")

• あれ？　この考え方、離心率の話と関係してくる?
  【数理考古学】離心率①二次曲線（楕円，放物線，双曲線）の極座標表示からの出発。
  
  離心率0($\frac{1}{1±0cos(θ)}$)=**半径1の単位円$e^{iθ},e^{-iθ}$の場合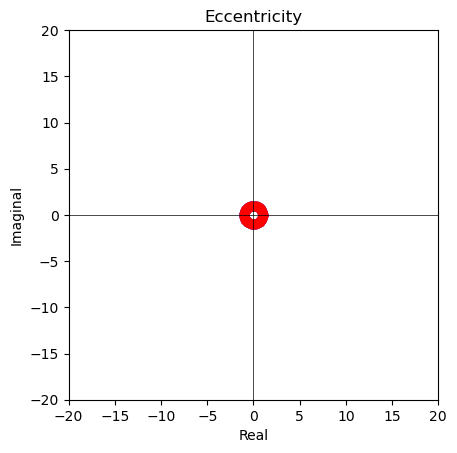
  
  離心率1($\frac{1}{1±1cos(θ)}$)=放物線$y=\sqrt{\frac{1}{2}-x},\sqrt{\frac{1}{2}+x}$の場合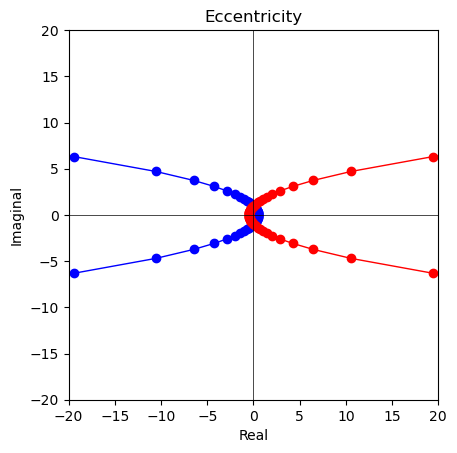
  
  これを90度反時計まわりに回転させると(xとyを入れ替えると)放物線$y=\frac{1}{2}-x^2,x^2-\frac{1}{2}$となる。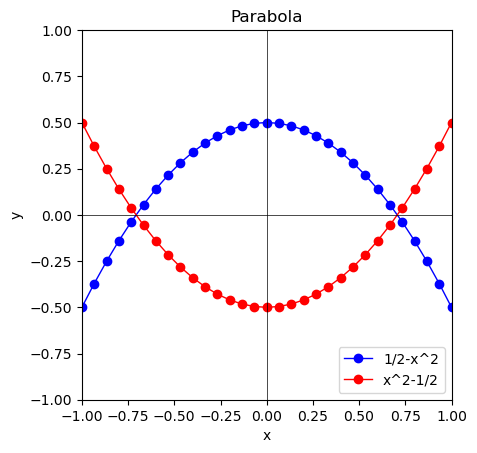
  

①統計学上の分散(Variance)$σ^2$の概念から出発する。
【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?

• 標本分散(Sample Dispersion)…偏差^2の合計/標本数

s^2 = \frac{1}{n}\sum_{i=1}^{n}  (x_i – \bar{x})^2

• 標本偏差(Sample Dispersion)…標本分散の平方根

s = \sqrt{\frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}

• 不偏分散(Unbiased Dispersion)…偏差^2の合計/（標本数-1）

s^2 = \frac{1}{n-1}\sum_{i=1}^{n}  (x_i – \bar{x})^2

• 標準偏差(Standard Deviation)…不偏分散の平方根

S = \sqrt{\frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}

②それは二次関数$x^2+2xy+y^2$でいうと内積(Innner Product)、すなわちx=0(平均)の場合の$y^2$($偏差^2$)に該当する。
【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?

\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\y
\end{bmatrix}
=x^2+2xy+y^2\\
\begin{bmatrix}
x & y
\end{bmatrix}
\begin{bmatrix}
0 & 0 \\
0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\y
\end{bmatrix}
=y^2

$\sqrt{x^2}=x$があまりに自明の場合(Trival Case)っぽく見えるので、それがユークリッド距離演算$\sqrt{0+x^2}$によって等長性が保証された空間への射影とも見て取れる事をつい失念してしまいます。そもそも、それら全てがいわゆる正規分布のBellCurve自体がこの方法によって(極座標系における)円状分布から平面に射影された結果である事に対応しているのですね。
【初心者向け】正規分布(Normal Distribution)とは何か？

③そして上掲の「離心率推移過程において楕円と双曲線の間に現れる放物線における符号逆転」に注意してその指数写像$y=e^{-x^2}$を求めると正規分布(Normal Distribution)の基本ベルカーブ(Bell Curve, 平均値0を中心とする左右対称の釣鐘形)が頂点を1とする形で現れる(同時に「それ自体は観測原点0同様到達不可能な観測限界∞」が「水平に広がる最外縁円周」として可視化される)。

y=(1 - \frac{x^2}{N})^N,-(1 - \frac{x^2}{N})^N

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#放物線x
x=np.linspace(-5,5,31,endpoint = True)

#描画関数
def parabola01(n): 
    plt.cla()
    #関数計算
    y= (1+(-x**2)/Time_Code[n])**Time_Code[n]
    #描画
    plt.plot(x,-y,color="red",marker="o",lw=1,label="-(1-x^2/n)^n")
    plt.plot(x,y,color="blue",marker="o",lw=1,label="+(1-x^2/n)^n")
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-5,5])
    plt.ylim([-5,5])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("Parabola")
    ax.legend(loc='lower right')
    
Time_Code=[1,2,3,4,5,6,7,8,9,10,11,12,13,14]

#parabola01(0)
#plt.show()

ani = animation.FuncAnimation(fig, parabola01, interval=100,frames=len(Time_Code))
ani.save("parabola06.gif", writer="pillow")

• N=1の時$y=±(1-x^2)。正負のグラフの交点は自明の場合(Trival Case)として(1,0)(-1,0)となる。
  
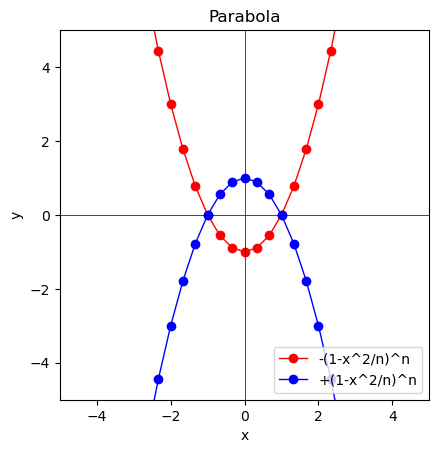
• N=2の時$±(1-\frac{x^2}{2})^2$
  
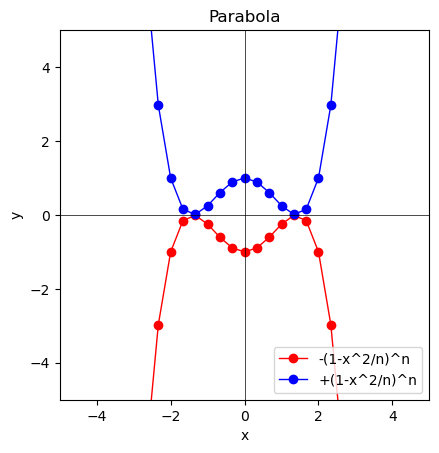
• N=3の時$±(1-\frac{x^2}{3})^3$
  
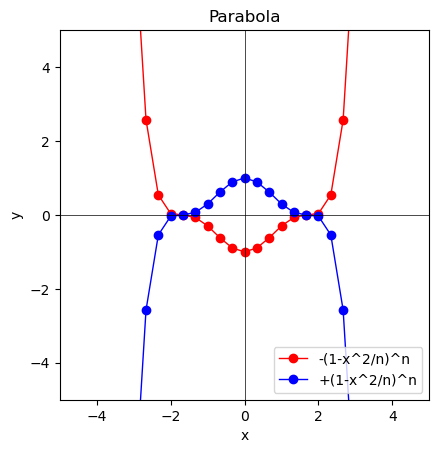
• 以降はこの繰り返しで裾野が-∞および+∞に向けてひたすら拡張し続ける。

これを過去投稿で述べた同心環(Concentric Ring)の世界に持ち込んでみましょう。$x^2$の逆数が$\sqrt{x}$となるのがヒントになりそうです。

import sympy as sp
x,y = sp.symbols('x,y')

#積分(-∞~∞)x^2
o1=sp.Integral(sp.exp(-x**2),(x,-sp.oo,sp.oo))**2
o2=o1.doit()
o3=sp.integrate(sp.exp(-x**2),(x,-sp.oo,sp.oo))**2
#積分(-∞~∞)
a1=sp.Integral(sp.exp(-x**2),(x,-sp.oo,sp.oo))
a2=a1.doit()
a3=sp.integrate(sp.exp(-x**2),(x,-sp.oo,sp.oo))
#積分(0~∞)
b1=sp.Integral(sp.exp(-x**2),(x,0,sp.oo))
b2=b1.doit()
b3=sp.integrate(sp.exp(-x**2),(x,0,sp.oo))
#積分(0~x)
c1=sp.Integral(sp.exp(-x**2),(x,0,x))
c2=c1.doit()
c3=sp.integrate(sp.exp(-x**2),(x,0,x))
c4=sp.erf(sp.oo)

#erf関数の微分
d1=sp.Derivative(sp.erf(x),x)
d2=d1.doit()
d3=sp.diff(sp.erf(x),x)

sp.init_printing()
display(o1) 
print(sp.latex(o1))
display(o2) 
print(sp.latex(o2))
display(o3) 
print(sp.latex(o3))
display(a1) 
print(sp.latex(a1))
display(a2) 
print(sp.latex(a2))
display(a3) 
print(sp.latex(a3))
display(b1) 
print(sp.latex(b1))
display(b2) 
print(sp.latex(b2))
display(b3) 
print(sp.latex(b3))
display(c1) 
print(sp.latex(c1))
display(c2) 
print(sp.latex(c2))
display(c3) 
print(sp.latex(c3))
display(c4) 
print(sp.latex(c4))
display(d1) 
print(sp.latex(d1))
display(d2) 
print(sp.latex(d2))
display(d3) 
print(sp.latex(d3))

• xy座標上の半径1の単位円の面積πの矩形、すなわち微積分可能な2乗の形で表現する事から出発する。
  ガウス積分 - Wikipedia

\left(\int\limits_{-\infty}^{\infty} e^{- x^{2}}\, dx\right)^{2}=\pi\\
\int\limits_{-\infty}^{\infty} e^{- x^{2}}\, dx=\sqrt{\pi}

• その結果はΓ関数の値が$\frac{1}{2}$の場合に一致する。
  【Python演算処理】階乗と順列と組み合わせ
  これは指数写像$e^x$の以下の冪級数定義からも明らかである($\frac{1}{2}$の級数が出てくる)。
  行列指数関数 - Wikipedia

e^{x}=\sum _{k=0}^{\infty }{\frac {1}{k!}}x^{k}

• 実数列-∞~+∞の範囲の総面積が$\sqrt{\pi}$なので、その指数写像0~∞の範囲の総面積は半分の$\frac{\sqrt{\pi}}{2}$となる。

\int\limits_{0}^{\infty} e^{- x^{2}}\, dx=\frac{\sqrt{\pi}}{2}

ところでSympyでは0~xの範囲の面積を積分によって求め様とすると計算式に誤差関数(Error Function)が現れるのです。
【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。

\int\limits_{0}^{x} e^{- x^{2}}\, dx=\frac{\sqrt{\pi} \operatorname{erf}{\left(x \right)}}{2}

• 誤差関数の定義は以下。

\operatorname {erf} \left(x\right)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t\\
\operatorname {erf}(∞)=1\\
\frac{d}{d x} \operatorname{erf}{\left(x \right)}=\frac{2 e^{- x^{2}}}{\sqrt{\pi}}

• なので実際にはこう記してあるだけである。

\int\limits_{0}^{x} e^{- x^{2}}\, dx=\frac{\sqrt{\pi}}{2}*{\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t=\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t

すなわち

\frac {2}{\sqrt {\pi }}\int\limits_{0}^{x} e^{- x^{2}}\, dx=elf(x)

正規分布との対応

N(μ, σ2)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\quad (x\in \mathbb {R} )\\
\frac{x^2}{2σ^2}=t^2\\
x=\sqrt{2}σt\\
\frac{1}{2}erf(\frac{x}{\sqrt{2}σ})

誤差関数と正規分布

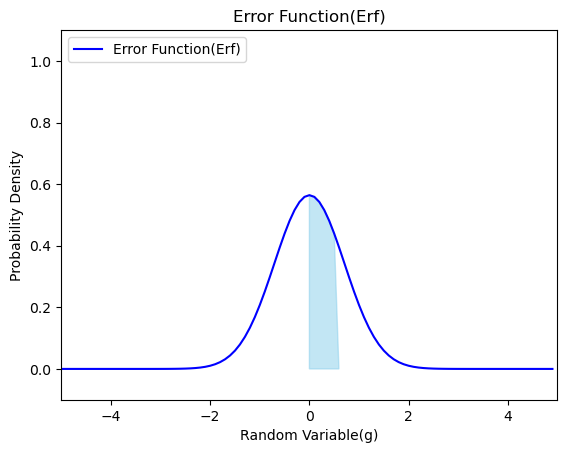
つまり，誤差関数とは（私の理解では），標準偏差が$\frac{1}{2}^{\frac{1}{2}}≒0.71$である正規分布の原点からaまでの領域の割合と言うことができます

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

#タイトル
TTL="Error Function(Erf)"
#とりあえずの有意最低限
Min=-5
#とりあえずの有意最大限
Max=5
# mean(平均)
MN = 0
# standard deviation(分散)
SCL = (1/2)**(1/2)

# 等差数列を生成
X = np.arange(start=Min, stop=Max, step=0.1)
#下側(左側)確率密度
LFTq=0.50 
#上側(右側)確率密度
RGTq=0.80 
#下側(左側)確率変数
LFT=stats.norm.ppf(LFTq, loc=MN, scale=SCL) 
#上側(右側)確率変数
RGT=stats.norm.ppf(RGTq, loc=MN, scale=SCL) 

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=MN, scale=SCL) # 期待値(平均)=0, 標準偏差(分散)=0.5 
norm_cdf = stats.norm.cdf(x=X, loc=MN, scale=SCL) # 期待値(平均)=0, 標準偏差(分散)=0.5 

x0=np.arange(start=LFT,stop=RGT,step=0.1)
xp=np.concatenate((
    [LFT],
    x0,
    [RGT,LFT])) 
yp=np.concatenate((
    [0],
    stats.norm.pdf(x=x0, loc=MN, scale=SCL),
    [0,0])) 

xc=np.concatenate((
    [LFT],
    x0,
    [RGT,LFT])) 
yc=np.concatenate((
    [0],
    stats.norm.cdf(x=x0, loc=MN, scale=SCL),
    [0,0])) 

plt.style.use('default')
fig = plt.figure()

# 可視化
plt.plot(X, norm_pdf,color="blue", label="Error Function(Erf)")
#plt.plot(X, norm_cdf,color="red", label="Cumulative Distribution Function(CDF)")
plt.fill(xp,yp,color="skyblue",alpha=0.5)
plt.ylim([-0.1,1.1])
plt.xlim([Min,Max])
plt.xlabel("Random Variable(g)")
plt.ylabel("Probability Density")
plt.title(TTL)
ax = fig.add_subplot(111)
ax.legend(loc='upper left')
plt.show()

要するにどうやら確率密度空間(Probability Density Space)や累積分布空間(Cumulative Distribution Space)とは同心環(Concentric Ring)の「角度の概念が既に存在する」計量ベクトル空間(Metric Vector Space)への「それがまだ有位未満の確率としてしか存在しない」スカラー(Scalar)写像に他ならない様なんです?
【Pyrhon演算処理】同心集合(Concentric Set)②加法的同心集合とは？

①円状分布(Circular Distribution)一つとっても大まかに分けて加法系(Even Scale)と乗法系(Logarithm Scale)が存在し、同心環においては「半径1の単位円(1次元トーラスたるリー群$S_0$=円周群=特殊直交座標系SO(2))を横軸とする実数列」といった形で偶奇性(Parity)を獲得しながら結び付けられる。


周期は1とは限らず2の場合も考えられ、この場合(奇数性を体現する)半周位置が整数外の$\frac{1}{2}$の位置に現れる(Γ関数概念の起源)。

• それは(球表面を等尺で覆う)球面座標系(特殊直交座標系SO(3))へと発展させられる。
  
  
  
  
  
  

• また大半径(Major Radius)と小半径(Minor Radius)が共に1の単位トーラス(Unit Torus,二次元トーラスたるリー群$S_1$)にも容易に発展させれ、その延長線上に四元数(Quaternion,三次元トーラスたるリー群$S_3$)が現れる。
  【数理考古学】群論とシミュレーション原理⑦三次元トーラスとしての四元数概念導入
  
  
  
  

②この時、縦軸座標と横軸座標の変換に使われる指数・対数写像(Exponential/Logarithm Map)が派生させる主要な球状分布(Spherical Distribution)として以下が挙げられる。

• 対蹠(点)を極限として設定する場合(一応はx軸、y軸、z軸それぞれに沿った観測が可能だが、方向の概念はまだない)
  【初心者向け】複素共役のアニメーション表示について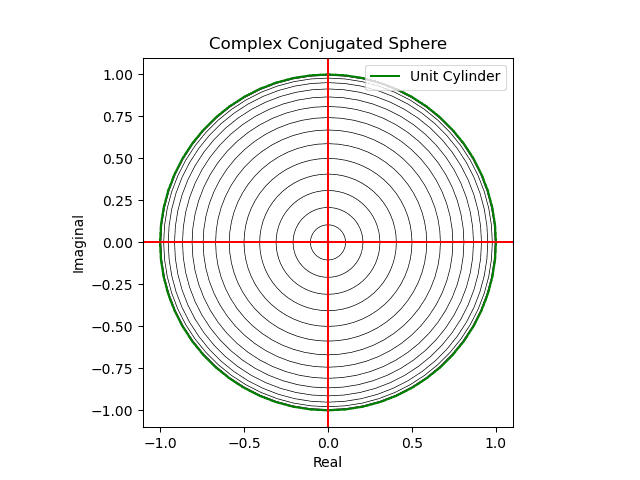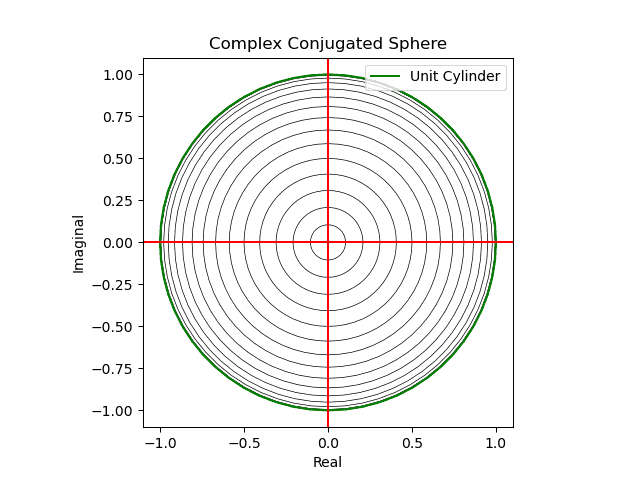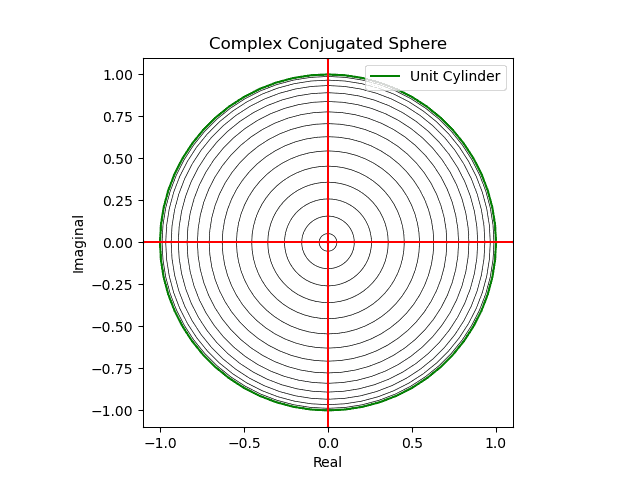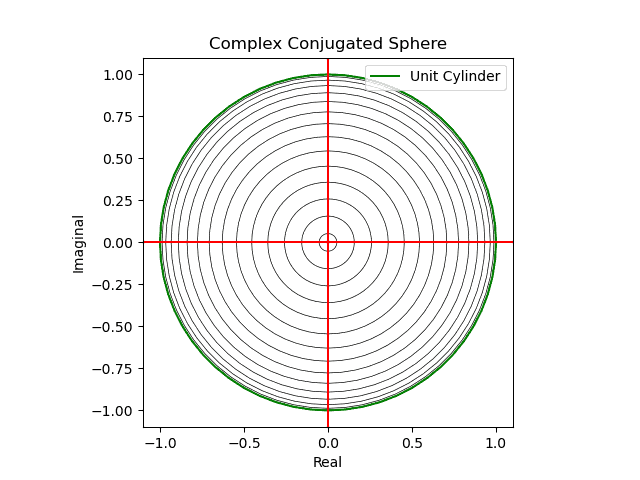
  
  
  

	実数列(円筒座標系の縦軸,等尺)	球状分布(球面尺)
0	-1(半径1)	-1(半径0)
1	0(半径1)	0(半径1)
2	1(半径1)	1(半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-1(半径1)","0(半径1)","1(半径1)"],
    ["-1(半径0)","0(半径1)","1(半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', '球状分布(球面尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

• 球状分布には含まれないが、トーラス座標系を上面から俯瞰すると「半径1の単位円を中心に0と2を半球の底辺(円弧)とする」$e^{xi}$座標系(両側対数尺)が現れる。
  

	同心環の水平軸(指数尺)	トーラス座標系の水平軸(両側対数尺)
0	exp(-1)	大半径0(小半径0)
1	exp(0)=1	大半径1(小半径1)
2	exp(1)	大半径2(小半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["exp(-1)","exp(0)=1","exp(1)"],
    ["大半径0(小半径0)","大半径1(小半径1)","大半径2(小半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['同心環の水平軸(指数尺)', 'トーラス座標系の水平軸(両側対数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

• 半球の底辺(円弧)を極限として設定する場合(方向の概念がまだないばかりか、正面図しか観測し得ない)。elf関数に正の実数を与えた場合に現れ、事実上空尺の座標系に対応する。
  【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。

	実数列(同心環の垂直軸,等尺)	Erf関数の写像(空尺)
0	観測原点0	半径0
1	観測限界∞	半径1

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["観測原点0","観測限界∞"],
    ["半径0","半径1"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(同心環の垂直軸,等尺)', 'Erf関数の写像(空尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

• ただでさえ人類にはこれまで進化の過程で獲得してきた認識能力の制約からこうした座標系の峻別に難点を抱えている上に(直感的に辺縁部の「裏側の景色」を誤差として切り捨ててしまう)、ここに「統計的有意水準(Statistical significance level)」なる新たな認識阻害要因が乱入してくる訳である。
  【数理考古学】とある実数列の規定例③オイラーの等式e^πi=-1が意味するもの？

$Z \geqq 1(z>1)$半球と$Z<1(z\leqq 1)$半球を峻別するリーマン球面も、こうした座標系のバリエーションの一つとして現れてくる訳です。
リーマン球面 - Wikipedia

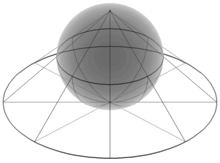
本来の半径1の円筒座標系(縦軸が等尺の実数列)から円錐座標系(縦軸=指数尺)への写像

	実数列(円筒座標系の縦軸,等尺)	円錐座標系の縦軸(指数尺)
0	-∞(半径1)	0(半径0)
1	-1(半径1)	exp(-1)
2	0(半径1)	1(半径1)
3	1(半径1)	exp(+1)
4	+∞(半径1)	∞(半径∞)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-∞(半径1)","-1(半径1)","0(半径1)","1(半径1)","+∞(半径1)"],
    ["0(半径0)","exp(-1)","1(半径1)","exp(+1)","∞(半径∞)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', '円錐座標系の縦軸(指数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

図の「特殊円錐座標系」で遂行されている写像

	実数列(円筒座標系の縦軸,等尺)	特殊円錐座標系の縦軸(両側対数尺)
0	-∞(半径1)	0(半径0)
1	-1(半径1)	exp(-1)
2	0(半径1)	1(半径1)
3	1(半径1)	exp(+1)
4	+∞(半径1)	2(半径π)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-∞(半径1)","-1(半径1)","0(半径1)","1(半径1)","+∞(半径1)"],
    ["0(半径0)","exp(-1)","1(半径1)","exp(+1)","2(半径π)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', '特殊円錐座標系の縦軸(両側対数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

「リーマン球面」への写像

	実数列(円筒座標系の縦軸,等尺)	リーマン球面の縦軸(両側対数尺)
0	-∞(半径1)	0(半径0)
1	-1(半径1)	exp(-1)
2	0(半径1)	1(半径1)
3	1(半径1)	exp(+1)
4	+∞(半径1)	2(半径0)

import numpy as np
import sympy as sp
import pandas as pd
X1 = np.matrix([
    ["-∞(半径1)","-1(半径1)","0(半径1)","1(半径1)","+∞(半径1)"],
    ["0(半径0)","exp(-1)","1(半径1)","exp(+1)","2(半径0)"]])
x=X1.transpose()
df=pd.DataFrame(x,columns=['実数列(円筒座標系の縦軸,等尺)', 'リーマン球面の縦軸(両側対数尺)'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))

実際、リーマン球面とは上掲の同心環が空環と重なる場合(すなわちそれ自体は観測不可能な観測原点0と観測限界∞を両端とする指数写像)と一致するのです。

こうして全体像を俯瞰してみると、どうやら(統計的に有意でない誤差や仮説の切り捨てに正規分布を使う)確率密度関数(PDF=Probability Density Function)や累積分布関数(CDF=Cumulative Distribution Function)の世界自体はしっかり物理的=幾何学的背景を備えている様に思えてくるのです。
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

• 水平軸（総乗が1となる乗法群）…足し合わせると1になる確率密度分布のp値。可能範囲としては-∞~+∞の範囲に広がるが、極限中心定理によって平均0から外れるほどその出現率は低減していく。
• 垂直軸(総和が0となる加法群)…データを最低値から最大値にかけて並べた確率変数x。平均μ=0,分散$σ^2$=1の標準分布(Normal Distribution)への射影によってデータを標準化する(単位を揃える)Z値$\frac{x-μ}{σ}$の考え方もある。
  【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?

さて、それでは実際に分散の概念は元情報のどの部分を保存し、どの部分を失ったり変質させてしてしまうのでしょうか？　どうやら以下の記事辺りに重要なヒントが？
目指せスーパーデータサイエンティスト(回帰分析編)

そんな感じで以下続報…