【Pyrhon演算処理】同心集合(Concentric Set)②加法的同心集合(Additive Concentric Set)とは？

前回の投稿は「小学校の算数の授業で習った数直線=スカラーの推移のみを抽出した同心円集合」から出発しました。
【Pyrhon演算処理】同心集合(Concentric Set)について。①乗法的同心集合(Multiplicative Concentric Set)とは？

しかし残念ながら最初に着手した乗法的同心集合(Multiplicative Concentric Set)は、どれとしてこの形に到達できなかったばかりか、その本質に近づくほど増率が増して同じものとは見えなくなっていったのです。

• 正方形が構築する同心円集合(演算$2^{\frac{n}{2}}$の結果集合)
  
• 球面の半径が構築する同心集合の一例(演算$\sqrt{3}*2^{\frac{n}{2}}$の結果集合)
  
• 正三角形が構築する同心円集合(演算$2^n$の結果集合)
  
• 演算$2^n$の結果集合
  
• 演算$e^n$の結果集合
  

この問題を解決するには加法群(Additive Group)概念の導入、あるいは(演算としてスカラー倍と加減算が保証された)ベクトル空間(Vector Space)への移行が必須となるのです。

加法的同心集合(Additive Concentric Set)

さっそく同心集合の加法群定義に入りたいと思います。
【数理考古学】群論概念(Group Theory Concept)①基本定義

• まずは元集合Aを用意する。例えばそれは乗法単位元(Multiplicative Identity)1を備えた乗法群(Multiplicative Group)であっても良い。
  

ついでに世界の方を回すインチキ回転から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(0,2,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[0,2],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([rollx,rollx],[rolly,rolly],[0,2],color="blue",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([0,rollx],[0,rolly],[2,2],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([0.1,2.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=45, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1]
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder001.gif", writer="pillow")

• 加法単位元(Additive Identity)0と逆元(Inverse Element)$A^{-1}$を準備する。
  

ついでに世界の方を回すインチキ回転から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-2,0,1201,endpoint = True)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-2,61)
uz1=num.repeat(-1,61)
uz2=num.repeat(0,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[0,-2],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([rollx,rollx],[rolly,rolly],[0,-2],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[-2,-2],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-2.1,0.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=45, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder002.gif", writer="pillow")

• 全てを結合する。
  

ついでに世界の方を回すインチキ回転から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=45, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder003.gif", writer="pillow")

ところが、かかる群に単位円筒(Unit Cylinder)、すなわちピッチ(Pitch,周回ごとの回転単位)の概念を加えようとすると、ここに複素解析学における多価関数の分岐点（Branch Point,その点を中心とする任意の閉曲線に沿って一周する時、その函数が元の点における値が周回前と周回後で一致しないという意味で不連続となるような点)概念や分岐截線 (Branch Cut,とある多価函数から一つの枝を截り出す様なガウス平面上の曲線）概念と関連する形で偶奇性(Parity)の概念が登場してくるのです(当然の様に円周率πと虚数iが乱入)。
【Python演算処理】単位円筒(Unit Cylinder)を巡る数理

分岐点 (数学) - Wikipedia

分岐切断の典型例は、複素対数函数である。複素数を極形式で$z=r⋅e^{iθ}$と表すと、zの対数は$log(z)=\log{r}+iθ$となるが、θの取り方には明らかに不定性がある（θに2πの整数倍を加えた別の角を取ることができる）。

複素対数函数の分枝とは、ガウス平面内の適当な連結開集合に属する任意のzの対数を与える連続函数L(z)を言うが、特に対数函数の分枝は原点から無限遠点へ結ぶ任意の半直線（分岐切断）の補集合という形で存在する。分岐切断は目的に応じて都合の良いものを取るが、よく選ばれるのは負の実軸である。

複素対数函数は分岐切断との交点に2πiの跳躍不連続点を持つ。葉(Sheet,ガウス平面の無限個のコピー）を分岐切断に沿って貼り合せることにより、複素対数函数をその上で連続にすることができる。すなわち、各葉の上での対数の値が主値と2πiの各々の倍数分だけズレているようにしておくと、これら曲面は複素対数函数を連続にする一意的な方法のもとで、分岐切断に沿って互いに張り合わされる。変数が原点を周って動くごとに、対数函数は異なる分枝の上へ亘っていく。

• ちなみに自然対数の真数(Antilogarithm)が1または-1の場合は以下の様に規定される。
  log(-1)って、iπのように思えますが、実際は(2n+1)iπ?

{多価関数log(-1)=(2n+1)iπ(n \in \mathbb{Z})\\
z＝|z|＊e^{arg(z)＊i} → log(z)＝log|z|＋arg(z)＊i\\
log(ー1)＝log|ー1|＋arg(ー1)＊i＝(2n＋1)＊π＊i、(n \in \mathbb{Z})\\
一方log(1)=(2n)*π*i(n=0)=0}

現段階の私には厳密な定義など不可能ですが、ここでいう多価性概念は恐らく群定義の過程同様、「1角形の辺、すなわち円周角の多価性」辺りと関連してくるのです。
【Rで球面幾何学】単位円と単位球②円周角とは何か？

偶数群(Even Group)概念の起源

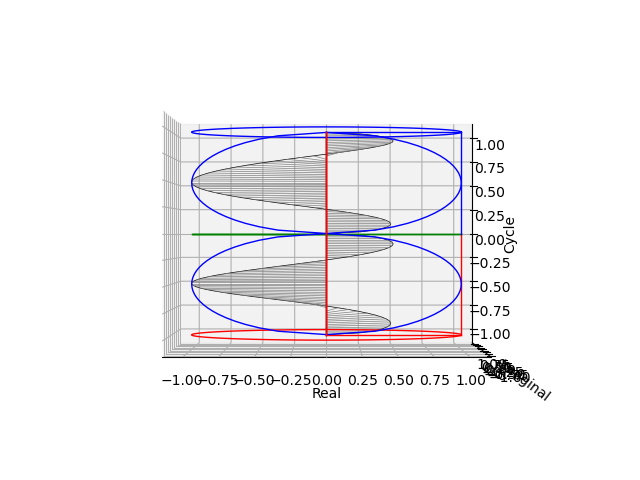
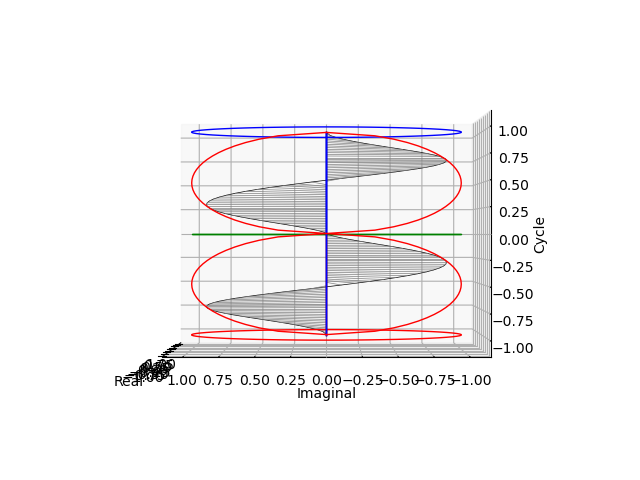
ピッチ1(周期1)の場合。ここでは仮にラップ級数(Rap Series)と呼ぶ以下の無限級数に対応。加法整数群の増減幅を1に定める案外重要な演算(Opreation)である。

{1^n(n=-\infty→+\infty)=(1,…,1,1,1,…,1)
}

その水平位置からの観測結果(周期1のcos(θ)cos⁡(θ)波とsin(θ)sin⁡(θ)波の検出)

cos(θ)波

sin(θ)波

ついでに世界の方を回すインチキ回転から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*4,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,121,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱とスポークの描画
    s2=[]
    for nm in range(len(c0)):
        s2.append(complex(m.cos(c0[nm]+Tcode[n]),m.sin(c0[nm]+Tcode[n])))
    s3=np.array(s2)
    ax.plot(s3.real,s3.imag,z0,color="black",lw=0.5)
    for nm in range(len(s3)):
        ax.plot([0,s3[nm].real],[0,s3[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="black",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="black",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="green",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1] 
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("uc001.gif", writer="pillow")

球面展開では以下となります。

【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！


$\sin(θ)\cos(θ)$波の検出

• 0/2πラジアンの時0
• ±$\frac{π}{2}$ラジアンの時$\frac{1}{2}$
• πラジアンの時-1

$\sin(θ)\sin(θ)$波の検出

• 0/2π/±$\frac{π}{2}$ラジアンの時0
• 半径±$\frac{1}{2}$の時に頂点

ついでに世界の方を回すインチキ展開から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円球データ準備
def src(x):
    return m.sqrt(1-x**2)
c1=num.linspace(0,m.pi*2,60,endpoint = False)
c2=num.linspace(0,m.pi*2,61,endpoint = True)
c0=num.concatenate([c1, c2])
z0=num.linspace(-1,1,121,endpoint = True)
zc1=num.linspace(-1,1,60,endpoint = False)
zc2=num.linspace(-1,1,61,endpoint = True)
zc=num.concatenate([zc1,zc2])

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiBH1=num.linspace(-1,1,30,endpoint = False)
MiBH2=num.linspace(-1,1,31,endpoint = True)
MiBH=num.concatenate([MiBH1,MiBH2])
MiBd=num.sqrt(1-MiBH**2)
MiHy=num.repeat(0,61)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円球とスポークの描画
    s0=[]
    for nm in range(len(c0)):
        s0.append(complex(m.cos(c0[nm]+Tcode[n])*src(zc[nm]),m.sin(c0[nm]+Tcode[n])*src(zc[nm])))
    s1=num.array(s0)
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #球面描画
    roll0=[]
    for nm in range(len(MiBd)):
        roll0.append(c.rect(MiBd[nm],Tcode[n]))
    roll=num.array(roll0)
    ax.plot(roll.real,roll.imag,MiHz,color="blue",lw=1)
    ax.plot(-roll.real,-roll.imag,MiHz,color="blue",lw=1)
    ax.plot(roll.imag,-roll.real,MiHz,color="red",lw=1)
    ax.plot(-roll.imag,roll.real,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cuberoll001.gif", writer="pillow")

奇数集合(Odd Set)概念の起源

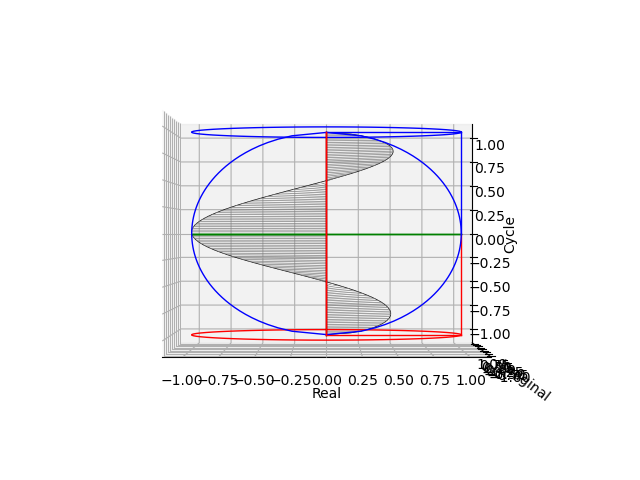
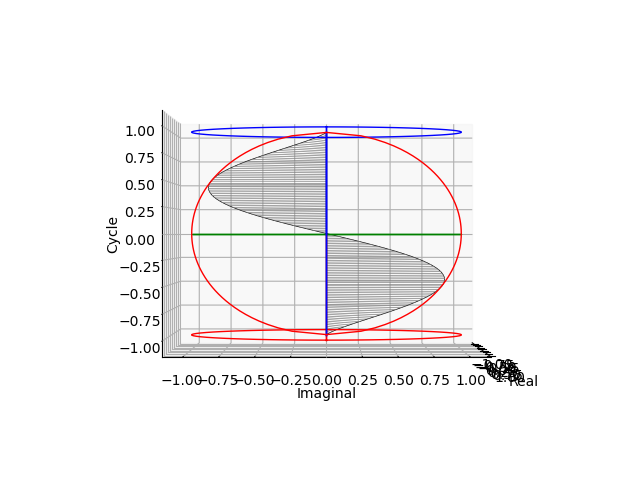
ピッチ$\frac{1}{2}$(周期1)の場合。交代級数(Alternating Series)概念に対応。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数

{-1^n(n=-\infty→+\infty)=(-1,…,1,-1,1,…,-1)
}

その水平位置からの観測結果(周期2のcos(θ)cos⁡(θ)波とsin(θ)sin⁡(θ)波の検出)

cos(θ)波

sin(θ)波

ついでに世界の方を回すインチキ回転から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*2,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,121,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱とスポークの描画
    s2=[]
    for nm in range(len(c0)):
        s2.append(complex(m.cos(c0[nm]+Tcode[n]),m.sin(c0[nm]+Tcode[n])))
    s3=np.array(s2)
    ax.plot(s3.real,s3.imag,z0,color="black",lw=0.5)
    for nm in range(len(s3)):
        ax.plot([0,s3[nm].real],[0,s3[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([-1,1],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([-1,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([-1,1],[0,0],[1,1],color="black",lw=1)
    ax.plot([1,1],[0,0],[-1,1],color="black",lw=1)
    ax.plot([-1,-1],[0,0],[-1,1],color="black",lw=1)
    #回転線追加
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,-rollx],[0,-rolly],[0,0],color="green",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("uc003.gif", writer="pillow")

同じく球面展開では以下となります。

【超わかる】オイラーの公式を見て！聞いて！感じるンゴ！


$\sin(θ)\cos(θ)$波の検出

• 0/2πラジアンの時0
• ±$\frac{π}{2}$ラジアンの時$\frac{1}{2}$
• πラジアンの時-1

$\sin(θ)\sin(θ)$波の検出

• 0/2π/±$\frac{π}{2}$ラジアンの時0
• 半径±$\frac{1}{2}$の時に頂点

ついでに世界の方を回すインチキ展開から脱却。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円球データ準備
def src(x):
    return m.sqrt(1-x**2)
c0=num.linspace(0,m.pi*2,121,endpoint = True)
zc=num.linspace(-1,1,121,endpoint = True)

#小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiBH=num.linspace(-1,1,61,endpoint = True)
MiBd=num.sqrt(1-MiBH**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円球とスポークの描画
    s0=[]
    for nm in range(len(c0)):
        s0.append(complex(m.cos(c0[nm]+Tcode[n])*src(zc[nm]),m.sin(c0[nm]+Tcode[n])*src(zc[nm])))
    s1=num.array(s0)
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,-1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #球面描画
    roll0=[]
    for nm in range(len(MiBd)):
        roll0.append(c.rect(MiBd[nm],Tcode[n]))
    roll=num.array(roll0)
    ax.plot(roll.real,roll.imag,MiHz,color="blue",lw=1)
    ax.plot(-roll.real,-roll.imag,MiHz,color="blue",lw=1)
    ax.plot(roll.imag,-roll.real,MiHz,color="red",lw=1)
    ax.plot(-roll.imag,roll.real,MiHz,color="red",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elv=10,0で水平、90で垂直)
    ax.view_init(elev=10, azim=-45)

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cuberoll101.gif", writer="pillow")

実軸(Real Axis)を成立させる為の虚軸(Imaginal Axis)設定方法自体は（それこそ「補助線」に過ぎないので）どの様な形にも設定可能ですが、どの場合でもこの「全体を周期1と見る単位円筒と周期2で見る単位円筒のセット」すなわち偶奇性(Parity)概念の導入だけは避けられない様です。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

偶数群(Even Group)

演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項0、公差±2、一般項±2nの両側無限数列を構成する。

Even_n(n=-\infty→0→+\infty)=(-\infty,…,-2n,…,-2×2=-4,-2×1=-2,-2×0=0,-2×1=2,-2×2=4,…,2n,…,+\infty)

• その演算は加減算の範囲で閉じており(偶数+偶数=偶数、偶数-偶数=偶数)、加法単位元と逆元を備え、かつ結合則(a+b)+c=a+(b+c)を満たす(元と単位元と逆元が同じ等差数列上に連続する)ので群の成立条件を満たす。
• 関数における偶関数は、その対称性ゆえに奇関数とと異なり逆関数を備えない。

奇数集合(Odd Set)

演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項1、公差±2、一般項±2n+1の両側無限数列を構成する。

Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n+1,…,-2×2+1=-3,-2×1+1=-1,2×0+1=1,2×1+1=3,…,2n+1,…,+\infty)

あるいは

Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n-1,…,-2×2-1=-5,-2×1-1=-3,2×0-1=-1,2×1-1=1,2×2-1=3,…,2n+1,…,+\infty)

• その演算は逆元を備え、結合則(a+b)+c=a+(b+c)も満たすものの、加法単位元0は集合範囲外で演算結果も閉じてない(奇数+奇数=偶数、奇数-奇数=偶数)。ゆえに群の成立条件を満たさない。
• 関数における奇関数も(その対称性ゆえにそれを備えない偶関数と異なり)逆関数を備え常に一対で現れる。また幾何学における(対蹠間を結ぶ直線が引けない)奇数角形の多角形もまた(それぞれ片側の対蹠にのみ接する)一対として現れる。

この様に「偶数の対称性」と「奇数の双極性」の対比は(それぞれ形を変えながら)あらゆる分野に普遍的に現れるのです。そして後者のCos(θ)の増減に注目すると固有ベクトル(Eigenvector)と固有値(Eigenvalue)概念の萌芽が見て取れるのです。

【初心者向け】方形描画関数①三角関数との関係。



こうして(規定演算によって球面座標系やトーラス座標系によって把握されてきた)元集合が、円柱座標系(Cylindrical Coordinate System)や円錐座標系(Conical Coordinate System)で扱える様になります。

円柱座標系(Cylindrical Coordinate System)

円筒座標系 - Wikipedia

与えられた点Pの位置を以下の三つの座標成分(p,φ,z)で表す。ただし基準平面からの「距離」はその点が基準平面の（表または裏の）どちら側に面するかによって正または負の値を持つものとする。

• 軸距離(Axial Distance)または動径距離(Radial Distance)ρ…z-軸から点 P までのユークリッド距離(別表現では「特別に選ばれた基準軸からの距離」);
• 方位角(Azimuth)φ…基準平面上の基準方向と原点から点Pの基準平面への正射影へ結んだ直線との間の角(別表現では「特別に選ばれた基準方向に対する軸から測った方向」);
• 軸座標(axial coordinate)または高さ(height)zは基準平面から点Pまでの符号付き距離(別表現では「基準軸に直交する特別に選ばれた基準平面からの距離」)。

円筒座標系の原点(origin)とは、上記三つの座標成分がすべて0として与えることができるような点を言う。これは上記の基準平面と基準軸の交点になる。 この基準軸は円筒軸(Cylindrical Axis; 円柱軸)や緯線(Longitudinal Axis) などと呼ばれ、極軸(Polar Axis)とは区別される（極軸あるいは始線とは、基準平面上に載っている半直線で、原点から出てその平面上の基準方向を指し示すものを表すために用いられる）。緯線に垂直な任意の方向を射線(Radial Lines;放射状の直線)と総称する。

円筒軸からの距離は動径距離(Radial Distance;放射距離)や動径(Radius) と呼ばれ、円筒軸周りの偏角座標は角度位置(Angular Position)や方位角(Azimuth)などと言う。動径成分と方位角成分を併せて極座標成分(Polar Coordinates)と言い、これはその点を通り基準平面に平行な平面上の二次元の極座標系に対応する。第三座標は基準平面を水平面と見るとき高さ(Height)や高度(Altitude)と呼んだり、緯度(Longitudinal Position)や軸位置(Axial Position)などとも言う。

• 「第三座標は基準平面を水平面と見るとき高さ(Height)や高度(Altitude)と呼んだり、緯度(Longitudinal Position)や軸位置(Axial Position)などとも言う。」…率直に「時間軸(t)」を含めない理由が分かりません。

円筒座標系は緯線周りの何らかの回転対称性を持つ物体や現象（例えば、丸い断面を持つ直線パイプを流れる水流や、金属円柱の熱分布、長い真っ直ぐなワイヤー内の電荷から出る電場、天文学における降着円盤など）との関連で有意である。

一方、この射影(Projection)によって副次的に生じる円錐座標系は、例えば元元が乗法群であった場合、その写像(Map)となる。
射影（projection）とは - IT用語辞典 e-Words
円錐の体積を円柱座標系で真面目に計算してみた

• 「円筒座標の導入自体は群規定導入以前でも可能である」なる考え方も不可能ではないが、こういう議論もあるのでその場合にどういう制限を受ける事になるかについて十分な追加記述を必要とするものとする。
• そういえば円錐座標系にも「HSV色空間モデル(Hue=色相,Saturation=彩度,Saturation=明度)」の様に逆元は備えていないが(あるいは元そのものとなるだけなので設定する意味がない)加法単位元(黒一色)と乗法単位元(基準色相環を実現する彩度と明度…あれ、次元それぞれに一つずつある？)なら備えている。こうした複雑な中間例が他にも幾らでも見つかりそうだったりする訳である。
  円錐座標系の意味・用法を知る
  彩度 - さいど | 武蔵野美術大学 造形ファイル
• そして、いわゆる「ヴェーバー‐フェヒナーの法則」に従うなら、例えば「HSV色空間モデル」も「音空間モデル」同様、その目盛りが均等尺(Even Scale)ではなく対数尺(Logarithmic Scale)かもしれないのである。
  【数理考古学】ヴェーバー‐フェヒナーの法則
  【数理考古学】「音階論」なる古くて新しい数理空間
  

かかる形での乗法群の加法群への写像がもたらす最大の恩恵は「傾き」の概念の追加というべきかもしれません。そう「(スカラー倍と加減算しか演算が存在しない)ベクトル空間」から「(角度や内積の概念が追加された)計量ベクトル空間」への拡張です。

傾き (数学) - Wikipedia

傾きmは傾斜角θによりm=tan(θ)と定義される。また平面上の直線の傾きは、垂直移動距離Δy($y_2-y_1$)を水平移動距離Δx($x_2-x_1$)で割ったm=Δy/Δxで定義される。

これらの等式が示す様に鉛直線（y軸に平行な直線）の傾きは、零除算となり、定義されない。

全体像としてはこういうイメージですね。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱高計算
    h1=2*n/len(uc)-1
    hz=np.repeat(h1,len(uc))
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #移動円追加
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[h1,h1],color="black",lw=0.5)
    ax.plot(uc.real,uc.imag,hz,color="black",lw=1)
    ax.plot([0,1],[0,0],[0,h1],color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=45, azim=Time_code[n])

#azimにTime_code(n)を設定すると世界の側が回る。
Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder003.gif", writer="pillow")

とりあえず「世界の方を回す」インチキ回転から脱却します。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱高計算
    h1=2*n/len(uc)-1
    hz=np.repeat(h1,len(uc))
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #移動円追加
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[h1,h1],color="purple",lw=0.5)
    ax.plot(uc.real,uc.imag,hz,color="purple",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,h1],color="purple",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=25,0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=25, azim=-45)

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Tcode))
ani.save("cylinder402.gif", writer="pillow")

【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

1次元球の体積は2rとなり、既知の結果と一致する。

これまでこうした表現を無条件で受容してきましたが、実は加法群が成立する裏側には単位円が隠れていた(直交、すなわち内積0となる形で交わっていた)という訳です。だから「十進法導入により周期を無限に細かく刻んでいく事によって実数列を近似する」といった方便が必要となった訳ですね。ある意味これこそが群論でいう「環(Ring)」概念そのもの？
【数理考古学】とある実数列(Real Sequance)の規定例①等差数列から加法整数群へ

ではこの考え方にこの投稿の主題たる同心集合の概念を重ねてみましょう。
【Pyrhon演算処理】同心集合(Concentric Set)について。①乗法的同心集合(Multiplicative Concentric Set)とは？

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱高計算
    h1=2*n/len(uc)-1
    hz=np.repeat(h1,len(uc))
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #半円柱描画
    ax.plot(s1.real/2,s1.imag/2,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #半単位円描画
    ax.plot(uc.real/2,uc.imag/2,uz0,color="red",lw=1)
    ax.plot(uc.real/2,uc.imag/2,uz1,color="green",lw=1)
    ax.plot(uc.real/2,uc.imag/2,uz2,color="blue",lw=1)    
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #半実数線追加
    ax.plot([1/2,1/2],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1/2,1/2],[0,0],[0,1],color="blue",lw=1)
    #移動円追加
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[h1,h1],color="black",lw=0.5)
    ax.plot(uc.real,uc.imag,hz,color="black",lw=1)
    ax.plot(uc.real/2,uc.imag/2,hz,color="black",lw=1)
    ax.plot([0,1],[0,0],[0,h1],color="black",lw=1)
    ax.plot([0,1/2],[0,0],[0,h1],color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder101.gif", writer="pillow")

こちらのプログラムも一応は「世界の方を回す」インチキ回転から脱却させておきましょう。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱高計算
    h1=2*n/len(uc)-1
    hz=np.repeat(h1,len(uc))
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
    #半円柱描画
    ax.plot(s1.real/2,s1.imag/2,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #半単位円描画
    ax.plot(uc.real/2,uc.imag/2,uz0,color="red",lw=1)
    ax.plot(uc.real/2,uc.imag/2,uz1,color="green",lw=1)
    ax.plot(uc.real/2,uc.imag/2,uz2,color="blue",lw=1)    
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #半実数線追加
    ax.plot([1/2,1/2],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1/2,1/2],[0,0],[0,1],color="blue",lw=1)
    #移動円追加
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[h1,h1],color="purple",lw=0.5)
    ax.plot(uc.real,uc.imag,hz,color="purple",lw=1)
    ax.plot(uc.real/2,uc.imag/2,hz,color="purple",lw=1)
    ax.plot([0,uc[n].real],[0,uc[n].imag],[0,h1],color="purple",lw=1)
    ax.plot([0,uc[n].real*1/2],[0,uc[n].imag*1/2],[0,h1],color="purple",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=25,0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=25, azim=-45)

Time_code0=np.arange(0,360,6) 
Time_code=Time_code0[::-1]   
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder501.gif", writer="pillow")

1を単位元とする乗法同心群は、その半径が極限たる0と∞(トーラス座標系ではさらに両者を同一視し、連結させて消してしまう!!)に差し掛かった時に計算不可能となりますが「傾き」概念にその特徴が継承されている事が分かります。

円筒座標系

円柱の中心軸からの半径方向（r軸）、周方向（θ軸）および円柱の軸方向（z軸）の3軸から構成される座標系のことで「円柱座標系」と呼ばれることもあります。

直交座標系(x,y,z)と円筒座標系(r,φ,z)の間には以下の関係が成り立ちます。

• x=r×cos(θ)
• y=r×sin(θ)
• z=z
• $r=\sqrt{x^2+y^2}$
• $φ=sign(y)atan2(y,x)$
• 表面積$S=2πr^2+2πrz$
• 体積$V=πr^2z$

import sympy as sp
import numpy as np
from sympy import I, pi, E
x,y,z,r,φ,m,S,V= sp.symbols('x,y,z,r,φ,m,S,V')

#sp.Eq(z,z)と書いてもTrueという
#論理演算結果が返るのみなので省略

#デカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
eq01=sp.Eq(r,sp.sqrt(x**2+y**2))
eq02=sp.Eq(φ,sp.sign(y)*sp.atan2(y,x))
eq03=sp.Eq(x,r*sp.cos(φ))
eq04=sp.Eq(y,r*sp.sin(φ))
eq05=sp.Eq(m,sp.tan(φ))
eq06=sp.Eq(m,z/r)
eq07=sp.Eq(S,2*pi*r**2+2*pi*r*z)
eq08=sp.Eq(V,pi*r**2*z)

#単位円(半径r=1)の場合
eq11=eq01.subs(r,1)
eq12=eq02.subs(r,1)
eq13=eq03.subs(r,1)
eq14=eq04.subs(r,1)
eq15=eq05.subs(r,1)
eq16=eq06.subs(r,1)
eq17=eq07.subs(r,1)
eq18=eq08.subs(r,1)

#tex
sp.init_printing()
print("デカルト座標系(x,y,z)と極座標系(r,φ,z)の相互変換")
display(eq01)
print(sp.latex(eq01))
display(eq02)
print(sp.latex(eq02))
display(eq03)
print(sp.latex(eq03))
display(eq04)
print(sp.latex(eq04))
display(eq05)
print(sp.latex(eq05))
display(eq06)
print(sp.latex(eq06))
display(eq07)
print(sp.latex(eq07))
display(eq08)
print(sp.latex(eq08))
print("単位円(半径r=1)の場合")
display(eq11)
print(sp.latex(eq11))
display(eq12)
print(sp.latex(eq12))
display(eq13)
print(sp.latex(eq13))
display(eq14)
print(sp.latex(eq14))
display(eq15)
print(sp.latex(eq15))
display(eq16)
print(sp.latex(eq16))
display(eq17)
print(sp.latex(eq17))
display(eq18)
print(sp.latex(eq18))

デカルト座標系(x,y,z)と極座標系(r,φ,z)の相互変換

\begin{align*}
&r = \sqrt{x^{2} + y^{2}}\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&x = r \cos{\left(φ \right)}\\
&y = r \sin{\left(φ \right)}\\
&z = z\\
&傾きm = \tan{\left(φ \right)}\\
&傾きm = \frac{z}{r}\\
&表面積S = 2 \pi r^{2} + 2 \pi r z\\
&体積V = \pi r^{2} z
\end{align*}

単位円(半径r=1)の場合(実数列$\mathbb{R}$そのものとなる)。

\begin{align*}
&r = 1\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&x = \cos{\left(φ \right)}\\
&y = \sin{\left(φ \right)}\\
&z = z\\
&傾きm = \tan{\left(φ \right)}\\
&傾きm = z\\
&表面積S = 2 \pi z + 2 \pi\\
&高さV = \pi z
\end{align*}

【Pyrhon演算処理】同心集合①乗法的同心集合とは？

大半径R、小半径rのトーラスの表面積は底面が半径rで高さが大半径の円周長2πRの円柱の側面積に等しく、体積はこの円柱と同値となる。

円錐座標系**(Conical Coordinate System)

上掲の様に「円柱座標系の特殊例」として現れます。式形としてはy=|x|など。
【Python演算処理】単位球面を巡る数理①とりあえず描画してみる。


これも世界の側を回すインチキ回転から脱却させておきましょう。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=np.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=np.array(s0)
z0=np.linspace(-1,1,1201,endpoint = True)

#「曲率」を計算
cv1=np.linspace(-1,1,1201,endpoint = True)
#cv1=num.sqrt(1-cv0**2)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.abs(cutz)
cuty=num.repeat(0,61)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(-1,61)
uz1=np.repeat(-0,61)
uz2=np.repeat(1,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=1)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #固定線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="black",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="black",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="black",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="black",lw=1)
    #回転線追加 
    rollx=c.rect(1,Tcode[n]).real
    rolly=c.rect(1,Tcode[n]).imag
    ax.plot([0,rollx],[0,rolly],[-1,-1],color="red",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[1,1],color="blue",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[-1,0],color="red",lw=1)
    ax.plot([rollx,rollx],[rolly,rolly],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot([rollx,0],[rolly,0],[-1,0],color="black",lw=1)
    ax.plot([0,rollx],[0,rolly],[0,1],color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=25、0にすると水平表示、90にすると垂直表示)
    ax.view_init(elev=25, azim=-45)

#azimにTime_code[n]を設定すると世界の側が回る。
Time_code0=np.arange(0,360,6)  
Time_code=Time_code0[::-1] 
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("corn001.gif", writer="pillow")

①平面図が観測者の主観によって「円錐の手前側と奥側の1周」にも「手前側の半周分を往復」にも見えますが、これは複素共役(Complex Conjugate)a±biの概念とも絡んでくる人間の認識能力のバグです。人間は例えば以下の画像に強引に「手前から奥/奥から手前に向かう波動」や「右回転/左回転」を見て取り、しかもその認識は首をちょっと振った程度でも揺らいでしまいますが、実はそもそも元アニメーションそのものにどちらか決定するのに必要な情報が欠け落ちているのです。
【初心者向け】複素共役のアニメーション表示について。



②また円錐座標系は実は以下の5種類存在しますが、それぞれの円錐対の軸が直交している(すなわち内積が0である)事が成立の条件となります。(しばしばトランプの札構成が例示されるが、行列演算の援用に際しては、しばしばそもそもの前提として正方性、すなわち行要素の数と列要素の数が一致する事を前提として問われる)。
直積集合 - Wikipedia

A×B=((a,b)|a \in A \land b \in B)

• 円錐軸が実数列(Real Sequence)…まさにこの投稿で扱ったケースで、1組の円錐対のみで構成される。逆を言えば以下の構成は全てその直積(Direct Product)で表せる？　その事について現段階では断言出来ないが、とにかく(内積概念が存在しない)ベクトル空間(Vector Space)で成立するのはこれのみで、以降の構成は全て計量ベクトル空間(Metric Vector Space)の成立を前提としている。
  計量ベクトル空間 - Wikipedia
• 円錐軸がxy軸…xy軸それぞれを軸線とする2組の円錐対によって構成される。xy=0、すなわちxかyが0の場合を特異点(Singular Point)とする開集合でもある。
• 円錐軸が平方対角線(Square Diagonal)…四象限を埋める2組の円錐対によって構成される。
• 円錐軸がxyz軸…xyz軸それぞれを軸線とする3組の円錐対によって構成される。
• 円錐軸が立方対角線(Cubic Diagonal)…八象限を埋める4組の円錐対によって構成される。xyz=0、すなわちxかyかzが0の場合を特異点(Singular Point)とする開集合でもある。

【初心者向け】線形関数や絶対値関数



こうして全体像を俯瞰した時、初めて「小学校の算数の授業で習った数直線=スカラーの推移のみを抽出した同心円集合」をより高次元の数学の領域で再掌握したといえるのかもしれません。そういう私自身、こうした考え方に辿り着く事によってやっと群論における環の概念を理解出来たのです（この理解で本当に数学的に合っているか、まだ全然自身がなかったりもする訳ったりもするのでしたすが。）

とりあえず、そんな感じで以下続報…