かつての投稿における「数直線=同心円=同心球面」のイメージより出発します。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
小学生の時習った数直線(Number Line)概念は、今から思えば原点の一点のみで固定されているだけなので、全体としては同心円/同心球面集合(Concentric Set)を構成するのです。考えてみればこれこそがスカラー(Scalar)概念そのものなんですね。
スカラー (数学) - Wikipedia
最も単純な2次元(xy面)上における同心円構造のイメージは以下となります。

import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
# 単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)
# 描画準備
fig = plt.figure()
ax = plt.axes()
def circle_draw(n):
plt.cla()
plt.title("Concentric Circles")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim([-4.0,4.0])
plt.xlim([-4.0,4.0])
# 同心円描画
plt.plot(0,0,marker='x', color='green')
circle1=patches.Circle((0,0),radius=1, fill=True, color='gray',lw=0.5,alpha=0.5)
circle2=patches.Circle((0,0),radius=2, fill=True, color='gray',lw=0.5,alpha=0.2)
circle3=patches.Circle((0,0),radius=3, fill=True, color='gray',lw=0.5,alpha=0.2)
circle4=patches.Circle((0,0),radius=4, fill=True, color='gray',lw=0.5,alpha=0.2)
circle5=patches.Circle((0,0),radius=5, fill=True, color='gray',lw=0.5,alpha=0.2)
circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)
ax.add_patch(circle1)
ax.add_patch(circle2)
ax.add_patch(circle3)
ax.add_patch(circle4)
ax.add_patch(circle5)
ax.add_patch(circle6)
ax.set_aspect('equal', adjustable='box')
#補助線描画
plt.axvline(0, 0, 1,color="black",lw=0.5)
plt.axhline(0, 0, 1,color="black",lw=0.5)
#移動線描画
plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
plt.plot(s1[n].real,s1[n].imag,marker='x', color='green')
plt.plot(s1[n].real*2,s1[n].imag*2,marker='x', color='green')
plt.plot(s1[n].real*3,s1[n].imag*3,marker='x', color='green')
plt.plot(s1[n].real*4,s1[n].imag*4,marker='x', color='green')
plt.plot(s1[n].real*5,s1[n].imag*5,marker='x', color='green')
plt.plot(s1[n].real*6,s1[n].imag*6,marker='x', color='green')
# circle_draw(1)
# plt.show()
ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw60001.gif", writer="pillow")
- このアニメーションで回転している線(数列)の定義は(それ自体は観測対象とならない)観測原点(Observation Origin)0を下限、観測限度(Observation Limit)を上限とする正の実数(非負実数)の開集合で、これまでの投稿では「自然数(Natural)を十進法概念導入によって実数列化した数列」と説明してきました。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
自然数同様、単位元も逆元も完備していませんが、どうしてそうなるかはその振る舞いを見ても一目瞭然としてきました。
【数理考古学】とある実数列の規定例③オイラーの等式が意味するもの?
どうやらとうとう、この部分から見直しを図らざるを得なくなった様なんです。
乗法的同心集合(Multiplicative Concentric Set)
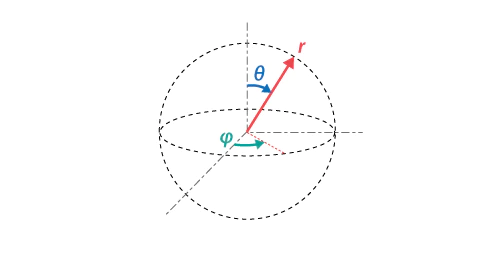
これを二次元極座標(r,φ)形式や三次元極座標(r,θ,φ)形式に拡張してみましょう。その全体像はスカラー=半径rと水平角φと垂直角θの関係関数として構成される形となります。
Python (SymPy) で方程式・連立方程式を解く、数列を求める
SymPy による数式処理
- ところで、これまでの投稿では角度を表すのに以下の関数を使ってきました。
atan2 - Wikipedia - ウィキペディア
\begin{align*}
&φ =\frac{\pi}{2} - \operatorname{atan_{2}}{\left(x,y \right)}\\
&θ =\frac{\pi}{2} - \operatorname{atan_{2}}{\left(\sqrt{x^{2} + y^{2} + z^{2}},z \right)}\\
&θ =\frac{\pi}{2} - \operatorname{atan_{2}}{r,z}\\
\end{align*}
- 以降の投稿では符号関数の概念を導入します。
符号関数(sign function)
\mathrm{sgn}x=\left\{\begin{matrix}
1\quad (x \gt 0)\\0\quad (x=0)\\
-1\quad (x \lt 0)\end{matrix}\right.
# モジュールをインポート
import numpy as np
import matplotlib.pyplot as plt
# フィギュアを設定
fig = plt.figure()
# グラフ描画領域を追加
ax = fig.add_subplot(111)
# グリッド線を表示
ax.grid(linestyle = "--")
# グラフタイトルを設定
ax.set_title("Sign Function", fontsize = 16)
# x軸, y軸のラベルを設定
ax.set_xlabel("x", fontsize = 16)
ax.set_ylabel("y", fontsize = 16)
# 区間 [-5, 5] を64分割
x = np.linspace(-5, 5, 64)
# y = sgn(x)
y = np.sign(x)
# 符号関数のグラフを描画
ax.plot(x, y, color = "darkblue")
- 結果として、使用関数は以下の様に修正される事になります。
\begin{align*}
&φ = \operatorname{atan_{2}}{(y,x)} \operatorname{sign}{(y)}
\\
&θ = \operatorname{atan_{2}}{(z,\sqrt{x^{2} + y^{2} + z^{2}})}\\
&θ = \operatorname{atan_{2}}{(z,r)}\\
\end{align*}
【Python演算処理】単位球面(Unit Shere)を巡る数理①とりあえず描画してみる。
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換
- 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
- $φ=siqn(y)\arctan^2(y,x)$
- $x=r×\cos(φ)$
- $y=r×\sin(φ)$
import sympy as sp
import numpy as np
from sympy import I, pi, E
x,y,r,φ= sp.symbols('x,y,r,φ')
# デカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
eq01=sp.Eq(r,sp.sqrt(x**2+y**2))
eq02=sp.Eq(φ,sp.sign(y)*sp.atan2(y,x))
eq03=sp.Eq(x,r*sp.cos(φ))
eq04=sp.Eq(y,r*sp.sin(φ))
# 単位円(半径r=1)の場合
eq11=eq01.subs(r,1)
eq12=eq02.subs(r,1)
eq13=eq03.subs(r,1)
eq14=eq04.subs(r,1)
# 単位方眼(x=y=1)に外接する場合
eq21=eq01.subs([(x,1),(y,1)]) #r=sqrt(2)
eq22=eq02.subs([(x,1),(y,1)]) #φ=π/4
# 極座標(r=sqrt(2),φ=π/4)の場合
eq23=eq03.subs([(r,sp.sqrt(2)),(φ,pi/4)]) #x=1
eq24=eq04.subs([(r,sp.sqrt(2)),(φ,pi/4)]) #y=1
# 極座標(r=sqrt(1),φ=π/4)の場合
eq33=eq03.subs([(r,1),(φ,pi/4)]) #x=sqrt(2)/2
eq34=eq04.subs([(r,1),(φ,pi/4)]) #y=sqrt(2)/2
# 単位方眼(x=y=1)に内接する場合
eq31=eq01.subs([(x,sp.sqrt(2)/2),(y,sp.sqrt(2)/2)]) #r=1
eq32=eq02.subs([(x,sp.sqrt(2)/2),(y,sp.sqrt(2)/2)]) #φ=π/4
# tex
sp.init_printing()
print("デカルト座標系(x,y)と極座標系(r,φ)の相互変換")
display(eq01)
print(sp.latex(eq01))
display(eq02)
print(sp.latex(eq02))
display(eq03)
print(sp.latex(eq03))
display(eq04)
print(sp.latex(eq04))
print("単位円(半径r=1)の場合")
display(eq11)
print(sp.latex(eq11))
display(eq12)
print(sp.latex(eq12))
display(eq13)
print(sp.latex(eq13))
display(eq14)
print(sp.latex(eq14))
print("単位方眼(x=y=z=1)に外接する場合")
display(eq21)
print(sp.latex(eq21))
display(eq22)
print(sp.latex(eq22))
print("極座標(r=sqrt(2),φ=π/4)の場合")
display(eq23)
print(sp.latex(eq23))
display(eq24)
print(sp.latex(eq24))
print("極座標(r=1,φ=π/4)の場合")
display(eq33)
print(sp.latex(eq33))
display(eq34)
print(sp.latex(eq34))
print("単位方眼(x=y=z=1)に内接する場合")
display(eq31)
print(sp.latex(eq31))
display(eq32)
print(sp.latex(eq32))
デカルト座標系(x,y)と極座標系(r,φ)の相互変換
\begin{align*}
&r = \sqrt{x^{2} + y^{2}}\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&x = r \cos{\left(φ \right)}\\
&y = r \sin{\left(φ \right)}
\end{align*}
単位円(半径r=1)の場合
\begin{align*}
&1 = \sqrt{x^{2} + y^{2}}\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&x = \cos{\left(φ \right)}\\
&y = \sin{\left(φ \right)}
\end{align*}
この辺りからおもむろに「同心円問題」が浮上してくる展開を迎えます。正方形の同心円集合を規定する演算は$E_n=2^{\frac{n}{2}}$となります。
- 単位方眼(x=y=z=1)に外接する場合
\begin{align*}
&r = \sqrt{2}\\
&φ = \frac{\pi}{4}\\
&x=1\\
&y=1
\end{align*}
- 単位方眼(x=y=z=1)に内接する場合
\begin{align*}
&r = 1\\
&φ = \frac{\pi}{4}\\
&x = \frac{\sqrt{2}}{2}\\
&y = \frac{\sqrt{2}}{2}
\end{align*}
演算$2^{\frac{n}{2}}$の結果集合としての$\frac{平方対角線}{2}$=同心円半径集合$e_n$の推移
E_n(n=-∞→0→+∞)=(E_{-∞}=\frac{1}{∞}=0,…,E_{-2}=2^{-\frac{2}{2}}=2^{-1}=\frac{1}{2},E_{-1}=2^{-\frac{1}{2}}=\frac{\sqrt{2}}{2},E_0=1,E_1=2^{\frac{1}{2}}=\sqrt{2},E_2=2^{\frac{2}{2}}=2^1=2,…,E_{+∞}=∞)
import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
# 単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)
# 描画準備
fig = plt.figure()
ax = plt.axes()
def circle_draw(n):
plt.cla()
plt.title("Concentric Circles")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim([-2.1,2.1])
plt.xlim([-2.1,2.1])
# 同心円描画
plt.plot(0,0,marker='x', color='green')
circle1=patches.Circle((0,0),radius=2, fill=True, color='gray',lw=0.5,alpha=0.5)
circle2=patches.Circle((0,0),radius=np.sqrt(2), fill=True, color='gray',lw=0.5,alpha=0.2)
circle3=patches.Circle((0,0),radius=1, fill=True, color='gray',lw=0.5,alpha=0.2)
circle4=patches.Circle((0,0),radius=1/np.sqrt(2), fill=True, color='gray',lw=0.5,alpha=0.2)
circle5=patches.Circle((0,0),radius=1/2, fill=True, color='gray',lw=0.5,alpha=0.2)
circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)
ax.add_patch(circle1)
ax.add_patch(circle2)
ax.add_patch(circle3)
ax.add_patch(circle4)
ax.add_patch(circle5)
ax.add_patch(circle6)
ax.set_aspect('equal', adjustable='box')
#補助線描画
plt.axvline(0, 0, 1,color="black",lw=0.5)
plt.axhline(0, 0, 1,color="black",lw=0.5)
#内内接立方体
plt.plot([-1/2,1/2],[1/2,1/2],color="gray",lw=1)
plt.plot([1/2,1/2],[1/2,-1/2],color="gray",lw=1)
plt.plot([1/2,-1/2],[-1/2,-1/2],color="gray",lw=1)
plt.plot([-1/2,-1/2],[-1/2,1/2],color="gray",lw=1)
#内接立方体
plt.plot([-np.sqrt(2)/2,np.sqrt(2)/2],[np.sqrt(2)/2,np.sqrt(2)/2],color="gray",lw=1)
plt.plot([np.sqrt(2)/2,np.sqrt(2)/2],[np.sqrt(2)/2,-np.sqrt(2)/2],color="gray",lw=1)
plt.plot([np.sqrt(2)/2,-np.sqrt(2)/2],[-np.sqrt(2)/2,-np.sqrt(2)/2],color="gray",lw=1)
plt.plot([-np.sqrt(2)/2,-np.sqrt(2)/2],[-np.sqrt(2)/2,np.sqrt(2)/2],color="gray",lw=1)
#単位立方体
plt.plot([-1,1],[1,1],color="black",lw=1)
plt.plot([1,1],[1,-1],color="black",lw=1)
plt.plot([1,-1],[-1,-1],color="black",lw=1)
plt.plot([-1,-1],[-1,1],color="black",lw=1)
#外接立方体
plt.plot([-np.sqrt(2),np.sqrt(2)],[np.sqrt(2),np.sqrt(2)],color="gray",lw=1)
plt.plot([np.sqrt(2),np.sqrt(2)],[np.sqrt(2),-np.sqrt(2)],color="gray",lw=1)
plt.plot([np.sqrt(2),-np.sqrt(2)],[-np.sqrt(2),-np.sqrt(2)],color="gray",lw=1)
plt.plot([-np.sqrt(2),-np.sqrt(2)],[-np.sqrt(2),np.sqrt(2)],color="gray",lw=1)
#外外接立方体
plt.plot([-2,2],[2,2],color="gray",lw=1)
plt.plot([2,2],[2,-2],color="gray",lw=1)
plt.plot([2,-2],[-2,-2],color="gray",lw=1)
plt.plot([-2,-2],[-2,2],color="gray",lw=1)
#移動線描画
plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
plt.plot(s1[n].real*2,s1[n].imag*2,marker='x', color='green')
plt.plot(s1[n].real*np.sqrt(2),s1[n].imag*np.sqrt(2),marker='x', color='green')
plt.plot(s1[n].real*1,s1[n].imag*1,marker='x', color='green')
plt.plot(s1[n].real*np.sqrt(2)/2,s1[n].imag*np.sqrt(2)/2,marker='x', color='green')
plt.plot(s1[n].real*1/2,s1[n].imag*1/2,marker='x', color='green')
# circle_draw(1)
# plt.show()
ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw70002.gif", writer="pillow")
三次元球面空間におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
- 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
- $φ=sign(y)\arctan^2(y,x)$
- $θ=\arctan^2(z,\sqrt{x^2+y^2+z^2})$
- $θ=\arctan^2(z,r)$
- $x=r×\sin(θ)\cos(φ)$
- $y=r×\sin(θ)\sin(φ)$
- $z=r×\cos(θ)$
import sympy as sp
import numpy as np
from sympy import I, pi, E
# プログラム中では色々試みてますが、
# 失敗に終わった試行も多く、全部は説明しません。
x,y,z,r,φ,θ = sp.symbols('x,y,z,r,φ,θ')
# デカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
eq01=sp.Eq(r,sp.sqrt(x**2+y**2+z**2))
eq02=sp.Eq(φ, sp.sign(y)*sp.atan2(y,x))
eq03=sp.Eq(θ, sp.atan2(z,sp.sqrt(x**2+y**2+z**2)))
eq03r=sp.Eq(θ,sp.atan2(z,r))
eq04=sp.Eq(x,r*sp.sin(θ)*sp.cos(φ) )
eq05=sp.Eq(y, r*sp.sin(θ)*sp.sin(φ))
eq06=sp.Eq(z, r*sp.cos(θ))
# s0=sp.solve([eq01, eq02,eq03,eq04,eq05,eq06],[r,φ,θ,x,y,z])
# 解けない(出力[])
# 単位球面(半径r=1)の場合
eq11=eq01.subs(r,1)
eq12=eq02.subs(r,1)
eq13r=eq03r.subs(r,1)
eq14=eq04.subs(r,1)
eq15=eq05.subs(r,1)
eq16=eq06.subs(r,1)
# 単位方眼(x=y=z=1)に内接する球面(半径r=1)について
# 角度φ=θ=pi/4ラジアンの位置を求めると
# 水平面(x,y)と垂直面(z)で結果が異なる。
eq24=eq04.subs([(r,1),(φ,pi/4),(θ,pi/4)])#x=1/2=2^-1
eq25=eq05.subs([(r,1),(φ,pi/4),(θ,pi/4)])#y=1/2=2^-1
eq26=eq06.subs([(r,1),(φ,pi/4),(θ,pi/4)])#z=sqrt(2)/2=2^-0.5
eq21a=eq01.subs([(x,1),(y,1),(z,1)]) #r=sqrt(3)sqrt(2)/2
eq22a=eq02.subs([(x,1),(y,1),(z,1)]) #φ=π/4ラジアン=45度
eq23a=eq03.subs([(x,1),(y,1),(z,1)]) #θ=π/6ラジアン=30度
# xyz座標(2,2,2)を通る内接球面
eq21d=eq01.subs([(x,2),(y,2),(z,2)]) #r=0.866025403784439=cos(π/6)=sin(π/3)
eq22d=eq02.subs([(x,2),(y,2),(z,2)]) #φ=0.785398163397448=π/4ラジアン=45度
eq23d=eq03.subs([(x,2),(y,2),(z,2)]) #θ=0.523598775598299=π/6ラジアン=30度
# xyz座標(1/2,1/2,1/2)を通る内接球面
eq21a=eq01.subs([(x,1/2),(y,1/2),(z,1/2)]) #r=0.866025403784439=cos(π/6)=sin(π/3)
eq22a=eq02.subs([(x,1/2),(y,1/2),(z,1/2)]) #φ=0.785398163397448=π/4ラジアン=45度
eq23a=eq03.subs([(x,1/2),(y,1/2),(z,1/2)]) #θ=0.523598775598299=π/6ラジアン=30度
# xyz座標(sqrt(2)/2,sqrt(2)/2,sqrt(2)/2)を通る内接球面
eq21b=eq01.subs([(x,sp.sqrt(2)/2),(y,sp.sqrt(2)/2),(z,sp.sqrt(2)/2)])#r=sqrt(3)sqrt(2)/2
eq22b=eq02.subs([(x,sp.sqrt(2)/2),(y,sp.sqrt(2)/2),(z,sp.sqrt(2)/2)])#φ=π/4ラジアン=45度
eq23b=eq03.subs([(x,sp.sqrt(2)/2),(y,sp.sqrt(2)/2),(z,sp.sqrt(2)/2)])#θ=π/6ラジアン=30度
# xyz座標(sqrt(2),sqrt(2),sqrt(2))を通る内接球面
eq21c=eq01.subs([(x,sp.sqrt(2)),(y,sp.sqrt(2)),(z,sp.sqrt(2))])#r=sqrt(3)sqrt(2)/2
eq22c=eq02.subs([(x,sp.sqrt(2)),(y,sp.sqrt(2)),(z,sp.sqrt(2))])#φ=π/4ラジアン=45度
eq23c=eq03.subs([(x,sp.sqrt(2)),(y,sp.sqrt(2)),(z,sp.sqrt(2))])#θ=π/6ラジアン=30度
# 単位球面に外接する立方体(半径r=sqrt(3))の場合
eq34=eq04.subs([(r,sp.sqrt(3)),(φ,pi/4),(θ,pi/4)])#x=sqrt(3)/2
eq35=eq05.subs([(r,sp.sqrt(3)),(φ,pi/4),(θ,pi/4)])#y=sqrt(3)/2
eq36=eq06.subs([(r,sp.sqrt(3)),(φ,pi/4),(θ,pi/4)])#z=sqrt(3)sqrt(2)/2
eq31=eq01.subs([(x,sp.sqrt(3)),(y,sp.sqrt(3)),(z,sp.sqrt(3))])#r=sqrt(3)sqrt(2)/2
eq32=eq02.subs([(x,sp.sqrt(3)),(y,sp.sqrt(3)),(z,sp.sqrt(3))])#φ=π/4ラジアン=45度
eq33=eq03.subs([(x,sp.sqrt(3)),(y,sp.sqrt(3)),(z,sp.sqrt(3))])#θ=π/6ラジアン=30度
# xyz座標(sqrt(3)/2,sqrt(3)/2,sqrt(3)/2)を通る内接球面
eq31a=eq01.subs([(x,sp.sqrt(3)/2),(y,sp.sqrt(3)/2),(z,sp.sqrt(3)/2)])#r=3/2
eq32a=eq02.subs([(x,sp.sqrt(3)/2),(y,sp.sqrt(3)/2),(z,sp.sqrt(3)/2)])#φ=π/4ラジアン=45度
eq33a=eq03.subs([(x,sp.sqrt(3)/2),(y,sp.sqrt(3)/2),(z,sp.sqrt(3)/2)])#θ=π/6ラジアン=30度
# xyz座標(sqrt(6)/2,sqrt(6)/2,sqrt(6)/2)を通る内接球面
eq31b=eq01.subs([(x,sp.sqrt(6)/2),(y,sp.sqrt(6)/2),(z,sp.sqrt(3)/2)])#r=sqrt(15)/2
eq32b=eq02.subs([(x,sp.sqrt(6)/2),(y,sp.sqrt(6)/2),(z,sp.sqrt(3)/2)])#φ=π/4ラジアン=45度
eq33b=eq03.subs([(x,sp.sqrt(6)/2),(y,sp.sqrt(6)/2),(z,sp.sqrt(3)/2)])#θ=atan(sqrt(5)/5)(1.150262)=65.90516度
# xyz座標(sqrt(6),sqrt(6),sqrt(6))を通る内接球面
eq31c=eq01.subs([(x,sp.sqrt(6)),(y,sp.sqrt(6)),(z,sp.sqrt(3))])#r=sqrt(15)/2
eq32c=eq02.subs([(x,sp.sqrt(6)),(y,sp.sqrt(6)),(z,sp.sqrt(3))])#φ=π/4ラジアン=45度
eq33c=eq03.subs([(x,sp.sqrt(6)),(y,sp.sqrt(6)),(z,sp.sqrt(3))])#θ=atan(sqrt(5)/5)(1.150262)=65.90516度
# 単位方眼(x=y=z=1)の場合
# eq21=eq01.subs([(x,1),(y,1),(z,1)])
# eq22=eq02.subs([(x,1),(y,1),(z,1)])
# eq23=eq03.subs([(x,1),(y,1),(z,1)])
# r=sqrt(1^2+1^2+1^2)=sqrt(3)
# φ=pi/2-atan2(1,1)=pi/2-pi/4=pi/4
# θ=pi/2-atan2(r,1)=pi/2-pi/3=pi/6
# この時点で既に異なる同心球面を指している。
# 極座標(r=sqrt(3),φ=π/4,θ=π/6)の場合
# eq24=eq04.subs([(r,sp.sqrt(3)),(φ,pi/4),(θ,pi/6)])
# eq25=eq05.subs([(r,sp.sqrt(3)),(φ,pi/4),(θ,pi/6)])
# eq26=eq06.subs([(r,sp.sqrt(3)),(φ,pi/4),(θ,pi/6)])
# cos(π/4)=sin(π/4)=sqrt(2)/2
# acos(sqrt(2)/2)=asin(sqrt(2)/2)=π/4
# cos(π/6)=sqrt(3)/2,acos(sqrt(3)/2)=π/6
# sin(π/6)=1/2,asin(1/2)=π/6
# 𝑥=𝑟sin(θ)cos(φ)=sqrt(3)*1/2*sqrt(2)/2=sqrt(6)/4
# 𝑦=𝑟sin(θ)sin(φ)=sqrt(3)*1/2*sqrt(2)/2=sqrt(6)/4
# z=𝑟cos(θ)=sqrt(3)*sqrt(3)/2=3/2
# 当然xy軸上の円弧の半径とz軸が示す半径は一致しない。
# tex
sp.init_printing()
print("デカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換")
display(eq01)
print(sp.latex(eq01))
display(eq02)
print(sp.latex(eq02))
display(eq03)
print(sp.latex(eq03))
display(eq03r)
print(sp.latex(eq03r))
display(eq04)
print(sp.latex(eq04))
display(eq05)
print(sp.latex(eq05))
display(eq06)
print(sp.latex(eq06))
print("単位球面(半径r=1)の場合")
display(eq11)
print(sp.latex(eq11))
display(eq12)
print(sp.latex(eq12))
display(eq13)
print(sp.latex(eq13))
display(eq14)
print(sp.latex(eq14))
display(eq15)
print(sp.latex(eq15))
display(eq16)
print(sp.latex(eq16))
print("単位方眼(x=y=z=1)に内接する球面の場合")
display(eq24)
print(sp.latex(eq24))
display(eq25)
print(sp.latex(eq25))
display(eq26)
print(sp.latex(eq26))
display(eq21)
print(sp.latex(eq21))
display(eq22)
print(sp.latex(eq22))
display(eq23)
print(sp.latex(eq23))
print("xyz座標(2,2,2)を通る内接球面")
display(eq21d)
print(sp.latex(eq21d))
display(eq22d)
print(sp.latex(eq22d))
display(eq23d)
print(sp.latex(eq23d))
print("xyz座標(1/2,1/2,1/2)を通る内接球面")
display(eq21a)
print(sp.latex(eq21a))
display(eq22a)
print(sp.latex(eq22a))
display(eq23a)
print(sp.latex(eq23a))
print("xyz座標(sqrt(2)/2,sqrt(2)/2,sqrt(2)/2)を通る内接球面")
display(eq21b)
print(sp.latex(eq21b))
display(eq22b)
print(sp.latex(eq22b))
display(eq23b)
print(sp.latex(eq23b))
print("xyz座標(sqrt(2),sqrt(2),sqrt(2))を通る内接球面")
display(eq21c)
print(sp.latex(eq21c))
display(eq22c)
print(sp.latex(eq22c))
display(eq23c)
print(sp.latex(eq23c))
print("単位方眼(x=y=Z=1)に外接する球面の場合")
display(eq34)
print(sp.latex(eq34))
display(eq35)
print(sp.latex(eq35))
display(eq36)
print(sp.latex(eq36))
display(eq31)
print(sp.latex(eq31))
display(eq32)
print(sp.latex(eq32))
display(eq33)
print(sp.latex(eq33))
print("xyz座標(sqrt(3)/2,sqrt(3)/2,sqrt(3)/2)を通る内接球面")
display(eq31a)
print(sp.latex(eq31a))
display(eq32a)
print(sp.latex(eq32a))
display(eq33a)
print(sp.latex(eq33a))
print("xyz座標(sqrt(6)/2,sqrt(6)/2,sqrt(6)/2)を通る内接球面")
display(eq31b)
print(sp.latex(eq31b))
display(eq32b)
print(sp.latex(eq32b))
display(eq33b)
print(sp.latex(eq33b))
print("xyz座標(sqrt(6),sqrt(6),sqrt(6))を通る内接球面")
display(eq31c)
print(sp.latex(eq31c))
display(eq32c)
print(sp.latex(eq32c))
display(eq33c)
print(sp.latex(eq33c))
デカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換の計算結果
\begin{align*}
&r = \sqrt{x^{2} + y^{2} + z^{2}}\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&θ = \operatorname{atan_{2}}{\left(z,\sqrt{x^{2} + y^{2} + z^{2}} \right)}\\
&θ = θ = \operatorname{atan_{2}}{\left(z,r \right)}\\
&x = r \sin{\left(θ \right)} \cos{\left(φ \right)}\\
&y = r \sin{\left(θ \right)} \sin{\left(φ \right)}\\
&z = r \cos{\left(θ \right)}
\end{align*}
単位円(半径r=1)の場合の計算結果
\begin{align*}
&1 = \sqrt{x^{2} + y^{2} + z^{2}}\\
&φ = \operatorname{atan_{2}}{\left(y,x \right)} \operatorname{sign}{\left(y \right)}\\
&θ = - \operatorname{atan_{2}}{\left(1,z \right)} + \frac{\pi}{2}\\
&x = \sin{\left(θ \right)} \cos{\left(φ \right)}\\
&y = \sin{\left(θ \right)} \sin{\left(φ \right)}\\
&z = \cos{\left(θ \right)}
\end{align*}
ついでに立方対角線に沿った同心円展開に挑戦してみましたが、あえなく座説。
| Axis(x,y,z) | Decimal A | Radius | Decimal R | |
|---|---|---|---|---|
| 0 | sqrt(6) | 2.44949000000000 | sqrt(15) | 3.87298300000000 |
| 1 | 2 | 2.00000000000000 | 2*sqrt(3) | 3.46410200000000 |
| 2 | sqrt(3) | 1.73205100000000 | sqrt(6)/2 | 1.22474500000000 |
| 3 | sqrt(2) | 1.41421400000000 | sqrt(6) | 2.44949000000000 |
| 4 | sqrt(6)/2 | 1.22474500000000 | sqrt(15)/2 | 1.93649200000000 |
| 5 | 1 | 1.00000000000000 | sqrt(6)/2 | 1.22474500000000 |
| 6 | sqrt(3)/2 | 0.866025400000000 | 3/2 | 1.50000000000000 |
| 7 | sqrt(2)/2 | 0.707106800000000 | sqrt(6)/2 | 1.22474500000000 |
| 8 | 1/2 | 0.500000000000000 | cos(π/6)/sin(π/3) | 0.866025400000000 |
import sympy as sp
import numpy as np
import pandas as pd
a,b,x,y = sp.symbols('a,b,x,y')
X1 = sp.Matrix([
["sqrt(6)","2","sqrt(3)","sqrt(2)","sqrt(6)/2","1","sqrt(3)/2","sqrt(2)/2","1/2"],
[2.44949,2.0,1.732051,1.414214,1.224745,1.0,0.8660254,0.7071068,0.5],
["sqrt(15)","2*sqrt(3)","sqrt(6)/2","sqrt(6)","sqrt(15)/2","sqrt(6)/2","3/2","sqrt(6)/2","cos(π/6)/sin(π/3)"],
[3.872983,3.464102,1.224745,2.44949,1.936492,1.224745,1.5,1.224745,0.8660254]])
x=X1.transpose()
df=pd.DataFrame(np.matrix(x),columns=['Axis(x,y,z)', 'Decimal A', 'Radius', 'Decimal R'])
sp.init_printing()
org=df.to_html()
print(org.replace('\n', ''))
特に理解不能なのが以下。どうして素直に45度($\frac{π}{4}$ラジアン)×3と展開してくれないんでしょうか?
単位方眼(x=y=z=1)に外接する球面の計算結果
\begin{align*}
&r =\sqrt{1^2+1^2+1^2}=\sqrt{3}\\
&φ =\frac{\pi}{2}-\operatorname{atan_{2}}{(1,1)}=\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4}\\
&θ = \frac{\pi}{2} - \operatorname{atan_{2}}{(\sqrt{3},1)} = \frac{\pi}{2}-\frac{\pi}{3}=\frac{\pi}{6}
\end{align*}
極座標($r=\sqrt{3},φ=\frac{π}{4},θ=\frac{π}{6}$)に対応するデカルト座標(x,y,z)
\begin{align*}
&\cos(\frac{π}{4})=\sin(\frac{π}{4})=\frac{\sqrt{2}}{2}\\
&\arccos(\frac{\sqrt{2}}{2})=\arcsin(\frac{\sqrt{2}}{2})=\frac{π}{4}\\
&\cos(\frac{π}{6})=\frac{\sqrt{3}}{2},\arccos(\frac{\sqrt{3}}{2})=\frac{π}{6}\\
&\sin(\frac{π}{6})=\frac{1}{2},\arcsin(\frac{1}{2})=\frac{π}{6}\\
すなわち\\
&x =𝑟*\sin(θ)*\cos(φ)=\sqrt{3}*\frac{1}{2}*\frac{\sqrt{2}}{2}=\frac{\sqrt{6}}{4}\\
&y =𝑟*\sin(θ)*\sin(φ)=\sqrt{3}*\frac{1}{2}*\frac{\sqrt{2}}{2}=\frac{\sqrt{6}}{4}\\
&z=𝑟*\cos(θ)=\sqrt{3}*\frac{\sqrt{3}}{2}=\frac{3}{2}
\end{align*}
とりあえず演算$E_n=\sqrt{3}2^{\frac{n}{2}}$の結果としての同心球集合の抽出には成功したので先に進む事にします。現段階ではイメージ構築の為に1系列に注目するのが精一杯ですが、考え方さえ整理出来たら他にもいくらでも見つかりそうな気がしています。
E_n(n=-∞→0→+∞)=\sqrt{3}2^{\frac{n}{2}}=(E_{-∞}=\frac{1}{∞}=0,…,E_{-2}=\sqrt{3}2^{-1}=\frac{\sqrt{3}}{2}),E_{-1}=\sqrt{3}2^{-0.5}=\frac{\sqrt{6}}{2}),E_{0}=\sqrt{3}2^{0}=\sqrt{3},E_{1}=\sqrt{3}2^{0.5}=\sqrt{6},E_{2}=\sqrt{3}2^{1}=2\sqrt{3},…,E_{∞+}=∞)
import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
# 単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)
# 描画準備
fig = plt.figure()
ax = plt.axes()
def circle_draw(n):
plt.cla()
plt.title("Concentric Circles")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim([-4.0,4.0])
plt.xlim([-4.0,4.0])
# 同心円描画
plt.plot(0,0,marker='x', color='green')
circle1=patches.Circle((0,0),radius=np.sqrt(3)/2, fill=True, color='gray',lw=0.5,alpha=0.5)
circle2=patches.Circle((0,0),radius=np.sqrt(6)/2, fill=True, color='gray',lw=0.5,alpha=0.2)
circle3=patches.Circle((0,0),radius=np.sqrt(3), fill=True, color='gray',lw=0.5,alpha=0.2)
circle4=patches.Circle((0,0),radius=np.sqrt(6), fill=True, color='gray',lw=0.5,alpha=0.2)
circle5=patches.Circle((0,0),radius=2*np.sqrt(3), fill=True, color='gray',lw=0.5,alpha=0.2)
circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)
ax.add_patch(circle1)
ax.add_patch(circle2)
ax.add_patch(circle3)
ax.add_patch(circle4)
ax.add_patch(circle5)
ax.add_patch(circle6)
ax.set_aspect('equal', adjustable='box')
#補助線描画
plt.axvline(0, 0, 1,color="black",lw=0.5)
plt.axhline(0, 0, 1,color="black",lw=0.5)
#移動線描画
plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
plt.plot(s1[n].real*np.sqrt(6)/2,s1[n].imag*np.sqrt(6)/2,marker='x', color='green')
plt.plot(s1[n].real*np.sqrt(3),s1[n].imag*np.sqrt(3),marker='x', color='green')
plt.plot(s1[n].real*np.sqrt(6),s1[n].imag*np.sqrt(6),marker='x', color='green')
plt.plot(s1[n].real*2*np.sqrt(3),s1[n].imag*2*np.sqrt(3),marker='x', color='green')
# circle_draw(1)
# plt.show()
ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw80002.gif", writer="pillow")
水平角φ(0~2π)の推移と垂直角θ(0~π)の推移を同期させると以下の様に見えます。
【Python演算処理】単位球面(Unit Shere)を巡る数理①とりあえず描画してみる。



とりあえず世界そのもを回転させるインチキ回転から脱却させておきましょう。



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutr=num.sqrt(1-cutz**2)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)
# 断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)
# タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
cutx0=[]
cuty0=[]
for nm in range(len(cutr)):
cutx0.append(c.rect(cutr[nm],Tcode[n]).real)
cuty0.append(c.rect(cutr[nm],Tcode[n]).imag)
cutx=num.array(cutx0)
cuty=num.array(cuty0)
ucutz=num.full(61,cutz[n])
#円柱描画
ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
#スポーク描画
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
for nm in range(len(uc)):
ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="purple",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#固定線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="purple",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#回転線描画
rollx=c.rect(1,Tcode[n]).real
rolly=c.rect(1,Tcode[n]).imag
ax.plot([0,rollx],[0,rolly],[0,0],color="purple",lw=1)
ax.plot([0,-rolly],[0,rollx],[0,0],color="blue",lw=1)
ax.plot([0,rolly],[0,-rollx],[0,0],color="red",lw=1)
#垂直断面線描画
ax.plot(cutx,cuty,cutz,color="purple",lw=1)
ax.plot(-1*cuty,cutx,cutz,color="blue",lw=1)
ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
ax.plot([0,cutx[n]],[0,cuty[n]],[cutz[n],cutz[n]],color="purple",lw=1)
ax.plot([0,-cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
ax.plot([0,cuty[n]],[0,-cutx[n]],[0,cutz[n]],color="red",lw=1)
#水平断面円描画
ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="purple",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elev=45,0にすると水平表示に)
ax.view_init(elev=45, azim=-45)
# azim=Time_code[n]と設定すると世界の側が回る。
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cube101.gif", writer="pillow")
ここで全体像をイメージする上での難所として浮上してくるのが、プログラム上球面はz座標区間(1~0~-1)を範囲とする同心円集合(半径0~1~0)として描画されるにも関わらず、各z座標における球面上の座標は$\cos(θ)$で与えられる辺り。
Z_n(n=1→0→-1)=(1,…,0,…,-1)\\
\cos(θ)(θ=0→\frac{π}{2}→πラジアン(rad(ian)))=Z_n\\
\arccos(Z_n)=(0,…,\frac{π}{2},…,πラジアン(rad(ian))
この関係式がしっかり頭に入ってないとすぐに行き詰まってしまうのです(それにつけても突如として自明の場合として割り込んでくるπ概念!!)。さらにはその同心球面展開を考えてみます。



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.sqrt(1-cutz**2)
cuty=num.repeat(0,61)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)
# 断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
ucutz=num.full(61,cutz[n])
#球面描画
ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
#半球面描画
ax.plot(s1.real*cv1/2,s1.imag*cv1/2,z0/2,color="gray",lw=0.5)
#スポーク描画
for nm in range(len(uc)):
ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="black",lw=0.5)
#半スポーク描画
#for nm in range(len(uc)):
# ax.plot([0,uc[nm].real*ucv[n]]/2,[0,uc[nm].imag*ucv[n]]/2,[cutz[n],cutz[n]]/2,color="black",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#半単位円描画
ax.plot(uc.real/2,uc.imag/2,uz0,color="red",lw=1)
ax.plot(uc.real/2,uc.imag/2,uz1,color="green",lw=1)
ax.plot(uc.real/2,uc.imag/2,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="purple",lw=1)
ax.plot([0,cutx[n]],[0,cuty[n]],[cutz[n],cutz[n]],color="purple",lw=1)
ax.plot([0,cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
ax.plot([0,cuty[n]],[0,-1*cutx[n]],[0,cutz[n]],color="red",lw=1)
ax.plot([0,1],[0,0],[0,0],color="purple",lw=1)
ax.plot([0,0],[0,1],[0,0],color="blue",lw=1)
ax.plot([0,0],[0,-1],[0,0],color="red",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#半実数線追加
ax.plot([1/2,1/2],[0,0],[-1,0],color="red",lw=1)
ax.plot([1/2,1/2],[0,0],[0,1],color="blue",lw=1)
#断面線描画
ax.plot(cutx,cuty,cutz,color="purple",lw=1)
ax.plot(cuty,cutx,cutz,color="blue",lw=1)
ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
#断面円描画
ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="black",lw=1)
#半断面円描画 ax.plot(uc.real*ucv[n]/2,uc.imag*ucv[n]/2,ucutz/2,color="black",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elev=0にすると水平表示、90にすると垂直表示)
ax.view_init(elev=45, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cylinder201.gif", writer="pillow")
こちらもとりあえず世界そのもを回転させるインチキ回転から脱却させておきましょう。



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutr=num.sqrt(1-cutz**2)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)
# 断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)
# タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
cutx0=[]
cuty0=[]
for nm in range(len(cutr)):
cutx0.append(c.rect(cutr[nm],Tcode[n]).real)
cuty0.append(c.rect(cutr[nm],Tcode[n]).imag)
cutx=num.array(cutx0)
cuty=num.array(cuty0)
ucutz=num.full(61,cutz[n])
#球面描画
ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
#半球面描画
ax.plot(s1.real*cv1/2,s1.imag*cv1/2,z0/2,color="gray",lw=0.5)
#スポーク描画
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
for nm in range(len(uc)):
ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="purple",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#半単位円描画
ax.plot(uc.real/2,uc.imag/2,uz0,color="red",lw=1)
ax.plot(uc.real/2,uc.imag/2,uz1,color="green",lw=1)
ax.plot(uc.real/2,uc.imag/2,uz2,color="blue",lw=1)
#固定線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="purple",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#回転線描画
rollx=c.rect(1,Tcode[n]).real
rolly=c.rect(1,Tcode[n]).imag
ax.plot([0,rollx],[0,rolly],[0,0],color="purple",lw=1)
ax.plot([0,-rolly],[0,rollx],[0,0],color="blue",lw=1)
ax.plot([0,rolly],[0,-rollx],[0,0],color="red",lw=1)
#垂直断面線描画
ax.plot(cutx,cuty,cutz,color="purple",lw=1)
ax.plot(-cuty,cutx,cutz,color="blue",lw=1)
ax.plot(cuty,-cutx,cutz,color="red",lw=1)
ax.plot([0,cutx[n]],[0,cuty[n]],[cutz[n],cutz[n]],color="purple",lw=1)
ax.plot([0,-cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
ax.plot([0,cuty[n]],[0,-cutx[n]],[0,cutz[n]],color="red",lw=1)
#半垂直断面線描画
ax.plot(cutx/2,cuty/2,cutz/2,color="purple",lw=1)
ax.plot(-cuty/2,cutx/2,cutz/2,color="blue",lw=1)
ax.plot(cuty/2,-cutx/2,cutz/2,color="red",lw=1)
ax.plot([0,cutx[n]/2],[0,cuty[n]/2],[cutz[n]/2,cutz[n]/2],color="purple",lw=1)
ax.plot([0,-cuty[n]/2],[0,cutx[n]/2],[0,cutz[n]/2],color="blue",lw=1)
ax.plot([0,cuty[n]/2],[0,-cutx[n]/2],[0,cutz[n]/2],color="red",lw=1)
#水平断面円描画
ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="purple",lw=1)
#半断面円描画
ax.plot(uc.real*ucv[n]/2,uc.imag*ucv[n]/2,ucutz/2,color="purple",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elev=45,0にすると水平表示に)
ax.view_init(elev=45, azim=-45)
# azim=Time_code[n]と設定すると世界の側が回る。
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("cube202.gif", writer="pillow")
- プログラム上半径1の球面と半径$\frac{1}{2}$の球面を対峙させましたが、比率としては半径2の円と半径1の円を対峙させた場合と変わりません。とどのつまりかかる同心円構造の半径は$2^n$乗のオーダーで増減する事が想定されます。
2^n(n=-\infty→0→+\infty)=(2^{-\infty}=\frac{1}{\infty}=0,…,2^{-2}=\frac{1}{2^2}=\frac{1}{4},2^{-1}=\frac{1}{2^1}=\frac{1}{2},2^{0}=\frac{2^1}{2^1}=1,2^1=1,2^2=4,…,2^{+\infty}=\infty)
import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
# 単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)
# 描画準備
fig = plt.figure()
ax = plt.axes()
def circle_draw(n):
plt.cla()
plt.title("Concentric Circles")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim([-4.0,4.0])
plt.xlim([-4.0,4.0])
# 同心円描画
plt.plot(0,0,marker='x', color='green')
circle1=patches.Circle((0,0),radius=1/4, fill=True, color='gray',lw=0.5,alpha=0.5)
circle2=patches.Circle((0,0),radius=1/2, fill=True, color='gray',lw=0.5,alpha=0.2)
circle3=patches.Circle((0,0),radius=1, fill=True, color='gray',lw=0.5,alpha=0.2)
circle4=patches.Circle((0,0),radius=2, fill=True, color='gray',lw=0.5,alpha=0.2)
circle5=patches.Circle((0,0),radius=4, fill=True, color='gray',lw=0.5,alpha=0.2)
circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)
ax.add_patch(circle1)
ax.add_patch(circle2)
ax.add_patch(circle3)
ax.add_patch(circle4)
ax.add_patch(circle5)
ax.add_patch(circle6)
ax.set_aspect('equal', adjustable='box')
#補助線描画
plt.axvline(0, 0, 1,color="black",lw=0.5)
plt.axhline(0, 0, 1,color="black",lw=0.5)
#移動線描画
plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
plt.plot(s1[n].real,s1[n].imag,marker='x', color='green')
plt.plot(s1[n].real*1/4,s1[n].imag*1/4,marker='x', color='green')
plt.plot(s1[n].real*1/2,s1[n].imag*1/2,marker='x', color='green')
plt.plot(s1[n].real*1,s1[n].imag*1,marker='x', color='green')
plt.plot(s1[n].real*2,s1[n].imag*2,marker='x', color='green')
plt.plot(s1[n].real*4,s1[n].imag*4,marker='x', color='green')
# circle_draw(1)
# plt.show()
ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw60003.gif", writer="pillow")
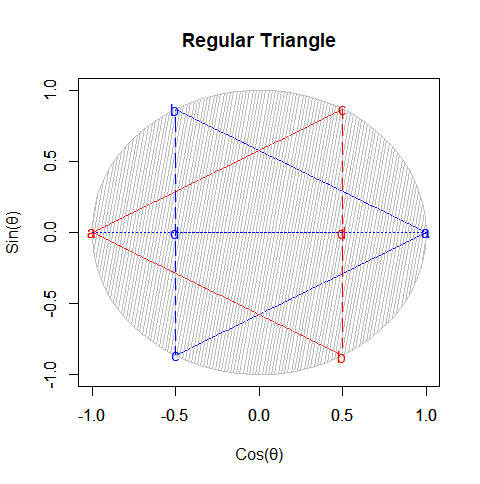
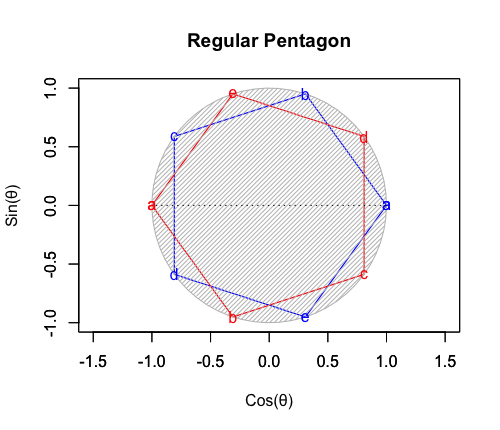
ちなみに演算$E_n=2^n$は正三角形の同心円集合をも規定します。そして正多角形のうち、この様な形で同心集合を構成するのは正三角形と正方形だけなのです。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間

import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
# 単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)
# 正弾角形データ作成
c1=np.linspace(-np.pi,np.pi,4,endpoint = True)
s2=[]
for num in range(len(c1)):
s2.append(complex(np.cos(c1[num]),np.sin(c1[num])))
s3=np.array(s2)
# 描画準備
fig = plt.figure()
ax = plt.axes()
def circle_draw(n):
plt.cla()
plt.title("Concentric Circles")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim([-2.1,2.1])
plt.xlim([-2.1,2.1])
# 同心円描画
plt.plot(0,0,marker='x', color='green')
circle1=patches.Circle((0,0),radius=4, fill=True, color='gray',lw=0.5,alpha=0.5)
circle2=patches.Circle((0,0),radius=2, fill=True, color='gray',lw=0.5,alpha=0.2)
circle3=patches.Circle((0,0),radius=1, fill=True, color='gray',lw=0.5,alpha=0.2)
circle4=patches.Circle((0,0),radius=1/2, fill=True, color='gray',lw=0.5,alpha=0.4)
circle5=patches.Circle((0,0),radius=1/4, fill=True, color='gray',lw=0.5,alpha=0.2)
circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)
ax.add_patch(circle1)
ax.add_patch(circle2)
ax.add_patch(circle3)
ax.add_patch(circle4)
ax.add_patch(circle5)
ax.add_patch(circle6)
ax.set_aspect('equal', adjustable='box')
#補助線描画
plt.axvline(0, 0, 1,color="gray",lw=0.5)
plt.axhline(0, 0, 1,color="gray",lw=0.5)
#正三角形(内接円1/4)
plt.plot(s3.real*1/4,s3.imag*1/4,color="gray",lw=1)
plt.plot(-s3.real*1/4,s3.imag*1/4,color="gray",lw=1)
#正三角形(内接円1.0)
plt.plot(s3.real*1/2,s3.imag*1/2,color="gray",lw=1)
plt.plot(-s3.real*1/2,s3.imag*1/2,color="gray",lw=1)
#正三角形(内接円1.0)
plt.plot(s3.real,s3.imag,color="black",lw=1)
plt.plot(-s3.real,s3.imag,color="black",lw=1)
#正三角形(内接円1.0)
plt.plot(s3.real*2,s3.imag*2,color="gray",lw=1)
plt.plot(-s3.real*2,s3.imag*2,color="gray",lw=1)
#正三角形(内接円1.0)
plt.plot(s3.real*4,s3.imag*4,color="gray",lw=1)
plt.plot(-s3.real*4,s3.imag*4,color="gray",lw=1)
#移動線描画
plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
plt.plot(s1[n].real*4,s1[n].imag*4,marker='x', color='green')
plt.plot(s1[n].real*2,s1[n].imag*2,marker='x', color='green')
plt.plot(s1[n].real*1,s1[n].imag*1,marker='x', color='green')
plt.plot(s1[n].real*1/2,s1[n].imag*1/2,marker='x', color='green')
plt.plot(s1[n].real*1/4,s1[n].imag*1/4,marker='x', color='green')
# circle_draw(1)
# plt.show()
ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw90008.gif", writer="pillow")
一方、全ての指数関数(Exponential Function)$a^n$は以下の変換式を用いて自然指数関数(Natural Exponential Function)$e^n$へと変換可能ですから、この比例関係は自然指数関数の一種と定義されます。
a^n=e^{n\log{a}}\\
2^n=e^{n\log{2}}\\
\log{2}=0.6931472
import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random
import matplotlib.patches as patches
import matplotlib.animation as animation
%matplotlib inline
# 単位円データ作成
c0=np.linspace(-np.pi,np.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(np.cos(c0[num]),np.sin(c0[num])))
s1=np.array(s0)
# 描画準備
fig = plt.figure()
ax = plt.axes()
def circle_draw(n):
plt.cla()
plt.title("Concentric Circles")
plt.xlabel("X")
plt.ylabel("Y")
plt.ylim([-4.0,4.0])
plt.xlim([-4.0,4.0])
# 同心円描画
plt.plot(0,0,marker='x', color='green')
circle1=patches.Circle((0,0),radius=np.exp(-2), fill=True, color='gray',lw=0.5,alpha=0.5)
circle2=patches.Circle((0,0),radius=np.exp(-1), fill=True, color='gray',lw=0.5,alpha=0.2)
circle3=patches.Circle((0,0),radius=np.exp(0), fill=True, color='gray',lw=0.5,alpha=0.2)
circle4=patches.Circle((0,0),radius=np.exp(1), fill=True, color='gray',lw=0.5,alpha=0.2)
circle5=patches.Circle((0,0),radius=np.exp(2), fill=True, color='gray',lw=0.5,alpha=0.2)
circle6=patches.Circle((0,0),radius=10, fill=True, color='gray',lw=0.5,alpha=0.2)
ax.add_patch(circle1)
ax.add_patch(circle2)
ax.add_patch(circle3)
ax.add_patch(circle4)
ax.add_patch(circle5)
ax.add_patch(circle6)
ax.set_aspect('equal', adjustable='box')
#補助線描画
plt.axvline(0, 0, 1,color="black",lw=0.5)
plt.axhline(0, 0, 1,color="black",lw=0.5)
#移動線描画
plt.plot([0,s1[n].real*6],[0,s1[n].imag*6],color="green",lw=1)
plt.plot(s1[n].real,s1[n].imag,marker='x', color='green')
plt.plot(s1[n].real*np.exp(-2),s1[n].imag*np.exp(-2),marker='x', color='green')
plt.plot(s1[n].real*np.exp(-1),s1[n].imag*np.exp(-1),marker='x', color='green')
plt.plot(s1[n].real*np.exp(0),s1[n].imag*np.exp(0),marker='x', color='green')
plt.plot(s1[n].real*np.exp(1),s1[n].imag*np.exp(1),marker='x', color='green')
plt.plot(s1[n].real*np.exp(2),s1[n].imag*np.exp(2),marker='x', color='green')
# circle_draw(1)
# plt.show()
ani = animation.FuncAnimation(fig, circle_draw, interval=50,frames=len(s1))
ani.save("circle_draw60004.gif", writer="pillow")
- $2^n$オーダーの同心円集合すら全体像を一望に収めるのが困難なくらいですから、さらに増率が加速度的に(それこそ文字通り指数関数的に)増大する$e^n$オーダーの同心円集合を納得のいく形で可視化するのはほぼ不可能です。
指数関数的と幾何級数的をざっくり振り返り - しかしまぁ、とりあえずはこれこそが「掛け算が足し算に、割り算が引き算に、冪乗算が掛け算に変換される」指数写像(Exponential Map)/対数写像(Logarithmic Map)の世界観という訳です。
【数理考古学】常用対数表を使った計算
どうやら以下と同じ事を言ってる様だ?
群同型写像(Group Isomorphism)とは、与えられた2つの群の元の一対一対応(One-to-One Correspondence,全単射あるいは直積?)において、それぞれの群演算を両立する全単射関数である。2つの群の間に同型写像が存在すればそれは同型(Isomorphic)と呼ばれ、群論の見地からは同じ性質を持つとされ区別する必要がなくなる。
全単射 - Wikipedia
逆を言えば圏論などではより厳格に「同型=等しい」とは考えないという事みたいです。
射 (圏論) - Wikipedia
加法実数群$(\mathbb{R},+)$は、すべての正の実数が乗法についてなす群$(\mathbb {R}^+,×)$に、同型写像$f(x)=e^x(x \in \mathbb{R})$によって同型である:
(\mathbb {R},+) \cong (\mathbb{R}^{+},×)
加法整数群$(\mathbb {Z},+)$は加法実数群$(\mathbb{R},+)$の部分群であり、商群$\frac{\mathbb{R}}{\mathbb{Z}}$は、同型写像$f(x+\mathbb {Z})=e^{2πxi}(x \in \mathbb{R})$によって絶対値1の乗法複素数群$S^1$に同型である(ここでいうS^1とは1次元トーラスでもあるリー群$S_1$の事では?):
\frac{(\mathbb{R},+)}{(\mathbb{Z},+)} \cong S^1
- こうした全体像を、以降は「乗法的同心円/球面集合(Multiplicative Concentric Set)」と呼び分けたいと思います。
ところで上掲の「乗法的同心円/球面集合」においては半径r=2(1)の同心円/球面の半径は2~0(1~0)の間、半径r=1($\frac{1}{2}$)の同心円/球面の半径は**1~0($\frac{1}{2}$~0)**の間を往復します。しかし我々の抱える一般的な同心円イメージにおいては、半径r=2(1)の同心円/球面の半径は2~1(1~$\frac{1}{2}$)の間、半径r=1($\frac{1}{2}$~0)の同心円/球面の半径は1~0($\frac{1}{2}$~0)の間を往復するのではないでしょうか? この期待にぴったり応えるのが(半径1を大半径=小半径とする)単位トーラス(Unit Torus)概念なのです。
【Python演算処理】単位トーラスを巡る数理①平坦トーラスとの往復



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)
# 小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)
# 小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,31,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])
# 小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
# 描画関数定義
def unit_cylinder(n):
plt.cla()
#断面計算
MiAvD0=[]
for nm in range(len(MiAvC)):
MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
MiAvD=num.array(MiAvD0)
MiBvD0=[]
for nm in range(len(MiBx)):
MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
MiBvD=num.array(MiBvD0)
MiCvD0=[]
for nm in range(len(MiHz)):
MiCvD0.append(c.rect(2,Tcode[n]))
MiCvD=num.array(MiCvD0)
#軌跡計算
Orb_r=abs(MiAvD[n])
Orb0=[]
for nm in range(len(MiCvD)):
Orb0.append(c.rect(Orb_r,Tcode[nm]))
Orbv=num.array(Orb0)
Orbh=num.repeat(MiAh[n],61)
#断面1計算
MiAvD10=[]
for nm in range(len(MiAvC)):
MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
MiAvD1=num.array(MiAvD10)
MiBvD10=[]
for nm in range(len(MiBx)):
MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
MiBvD1=num.array(MiBvD10)
MiCvD10=[]
for nm in range(len(MiHz)):
MiCvD10.append(c.rect(2,Tcode[0]))
MiCvD1=num.array(MiCvD10)
#円柱描画
ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
#中心線描画
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
#分割原点
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)
ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
#アニメーション描画
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)
ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="red",lw=1)
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
#軌跡描画
ax.plot(Orbv.real,Orbv.imag,Orbh,color="red",lw=1)
#諸元追加
ax.set_ylim([-2.1,2.1])
ax.set_xlim([-2.1,2.1])
ax.set_zlim([-2.1,2.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=25, azim=-45)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
# Time_code0=num.arange(0,360,6)
# Time_code=Time_code0[::-1]
# unit_cylinder(15)
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("torus001.gif", writer="pillow")
二分割トーラス
【Python演算処理】単位トーラスを巡る数理②トーラス群の設定



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)
# 小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)
# 小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,30,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])
# 小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
Tcode2=num.concatenate([Tcode[30:61], Tcode[0:29]])
# 描画関数定義
def unit_cylinder(n):
plt.cla()
#断面計算
MiAvD0=[]
for nm in range(len(MiAv)):
MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
MiAvD=num.array(MiAvD0)
MiBvD0=[]
for nm in range(len(MiBx)):
MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
MiBvD=num.array(MiBvD0)
MiCvD0=[]
for nm in range(len(MiHz)):
MiCvD0.append(c.rect(2,Tcode[n]))
MiCvD=num.array(MiCvD0)
#断面計算(対蹠)
MiDvD0=[]
for nm in range(len(MiAv)):
MiDvD0.append(c.rect(MiAv[nm],Tcode2[n]))
MiDvD=num.array(MiDvD0)
MiDvE=MiDvD[::-1]
MiEvD0=[]
for nm in range(len(MiBx)):
MiEvD0.append(c.rect(MiBx[nm],Tcode2[n]))
MiEvD=num.array(MiEvD0)
MiFvD0=[]
for nm in range(len(MiHz)):
MiFvD0.append(c.rect(2,Tcode2[n]))
MiFvD=num.array(MiFvD0)
ucA1=num.concatenate([uc[30:61], uc[0:29]])
#断面1計算
MiAvD10=[]
for nm in range(len(MiAvC)):
MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
MiAvD1=num.array(MiAvD10)
MiBvD10=[]
for nm in range(len(MiBx)):
MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
MiBvD1=num.array(MiBvD10)
MiCvD10=[]
for nm in range(len(MiHz)):
MiCvD10.append(c.rect(2,Tcode[0]))
MiCvD1=num.array(MiCvD10)
#断面2計算
MiAvD20=[]
for nm in range(len(MiAvC)):
MiAvD20.append(c.rect(MiAv[nm],Tcode[30]))
MiAvD2=num.array(MiAvD20)
MiBvD20=[]
for nm in range(len(MiBx)):
MiBvD20.append(c.rect(MiBx[nm],Tcode[30]))
MiBvD2=num.array(MiBvD20)
MiCvD20=[]
for nm in range(len(MiHz)):
MiCvD20.append(c.rect(2,Tcode[30]))
MiCvD2=num.array(MiCvD20)
#軌跡計算
Orb_r=abs(MiAvD[n])
Orb0=[]
for nm in range(len(MiCvD)):
Orb0.append(c.rect(Orb_r,Tcode[nm]))
Orbv=num.array(Orb0)
Orbh=num.repeat(MiAh[n],61)
#円柱描画
ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
#中心線描画
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
#断面1描画
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)
ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
#断面2描画
ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[-1,-1],color="purple",lw=1)
ax.plot([0,uc[30].real],[0,uc[30].imag],[0,0],color="blue",lw=1)
ax.plot([uc[30].real,MiCvD2[30].real],[uc[30].imag,MiCvD2[30].imag],[0,0],color="purple",lw=1)
ax.plot([uc[30].real,uc[30].real],[uc[30].imag,uc[30].imag],[-1,1],color="purple",lw=1)
ax.plot([uc[30].real,MiAvD2[30].real],[uc[30].imag,MiAvD2[30].imag],[0,MiAh[30]],color="purple",lw=1)
ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[1,1],color="purple",lw=1)
ax.plot([MiCvD2[30].real,MiCvD2[30].real],[MiCvD2[30].imag,MiCvD2[30].imag],[-1,1],color="purple",lw=1)
ax.plot(MiAvD2.real,MiAvD2.imag,MiAh,color="purple",lw=1)
ax.plot(MiBvD2.real,MiBvD2.imag,MiHz,color="blue",lw=1)
#アニメーション描画
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)
ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="green",lw=1)
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
#アニメーション描画(対蹠)
ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,ucA1[n].real],[0,ucA1[n].imag],[0,0],color="blue",lw=1)
ax.plot([ucA1[n].real,MiFvD[n].real],[ucA1[n].imag,MiFvD[n].imag],[0,0],color="black",lw=1)
ax.plot([ucA1[n].real,ucA1[n].real],[ucA1[n].imag,ucA1[n].imag],[-1,1],color="black",lw=1)
ax.plot([ucA1[n].real,MiDvE[n].real],[ucA1[n].imag,MiDvE[n].imag],[0,MiAh[n]],color="purple",lw=1)
ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiFvD[n].real,MiFvD[n].real],[MiFvD[n].imag,MiFvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiDvD.real,MiDvD.imag,MiAh,color="red",lw=1)
ax.plot(MiEvD.real,MiEvD.imag,MiHz,color="blue",lw=1)
#軌跡描画
ax.plot(Orbv.real,Orbv.imag,Orbh,color="red",lw=1)
#諸元追加
ax.set_ylim([-2.1,2.1])
ax.set_xlim([-2.1,2.1])
ax.set_zlim([-2.1,2.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elev=25,0で水平、90で垂直)
ax.view_init(elev=25, azim=-45)
# azimにTime_code(n)を設定すると世界の側が回る。
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
# Time_code0=num.arange(0,360,6)
# Time_code=Time_code0[::-1]
# unit_cylinder(15)
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("torus212.gif", writer="pillow")
三分割/六分割トーラス
上掲の様に三分割では正三角形が一対で現れるので事実上六分割となります(奇数正多角形に共通する特徴)。
【Rで球面幾何学】平方眼と立方眼の小宇宙について。
【Python演算処理】単位トーラスを巡る数理②トーラス群の設定



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)
# 小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)
# 小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,30,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])
# 小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
Tcode2=num.concatenate([Tcode[30:61], Tcode[0:29]])
# 描画関数定義
def unit_cylinder(n):
plt.cla()
#断面計算
MiAvD0=[]
for nm in range(len(MiAv)):
MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
MiAvD=num.array(MiAvD0)
MiBvD0=[]
for nm in range(len(MiBx)):
MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
MiBvD=num.array(MiBvD0)
MiCvD0=[]
for nm in range(len(MiHz)):
MiCvD0.append(c.rect(2,Tcode[n]))
MiCvD=num.array(MiCvD0)
#断面計算(対蹠)
MiDvD0=[]
for nm in range(len(MiAv)):
MiDvD0.append(c.rect(MiAv[nm],Tcode2[n]))
MiDvD=num.array(MiDvD0)
MiDvE=MiDvD[::-1]
MiEvD0=[]
for nm in range(len(MiBx)):
MiEvD0.append(c.rect(MiBx[nm],Tcode2[n]))
MiEvD=num.array(MiEvD0)
MiFvD0=[]
for nm in range(len(MiHz)):
MiFvD0.append(c.rect(2,Tcode2[n]))
MiFvD=num.array(MiFvD0)
ucA1=num.concatenate([uc[30:61], uc[0:29]])
#断面1計算
MiAvD10=[]
for nm in range(len(MiAvC)):
MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
MiAvD1=num.array(MiAvD10)
MiBvD10=[]
for nm in range(len(MiBx)):
MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
MiBvD1=num.array(MiBvD10)
MiCvD10=[]
for nm in range(len(MiHz)):
MiCvD10.append(c.rect(2,Tcode[0]))
MiCvD1=num.array(MiCvD10)
#断面2計算
MiAvD20=[]
for nm in range(len(MiAvC)):
MiAvD20.append(c.rect(MiAv[nm],Tcode[30]))
MiAvD2=num.array(MiAvD20)
MiBvD20=[]
for nm in range(len(MiBx)):
MiBvD20.append(c.rect(MiBx[nm],Tcode[30]))
MiBvD2=num.array(MiBvD20)
MiCvD20=[]
for nm in range(len(MiHz)):
MiCvD20.append(c.rect(2,Tcode[30]))
MiCvD2=num.array(MiCvD20)
#断面3計算
MiAvD30=[]
for nm in range(len(MiAvC)):
MiAvD30.append(c.rect(MiAv[nm],Tcode[10]))
MiAvD3=num.array(MiAvD30)
MiBvD30=[]
for nm in range(len(MiBx)):
MiBvD30.append(c.rect(MiBx[nm],Tcode[10]))
MiBvD3=num.array(MiBvD30)
MiCvD30=[]
for nm in range(len(MiHz)):
MiCvD30.append(c.rect(2,Tcode[10]))
MiCvD3=num.array(MiCvD30)
#断面4計算
MiAvD40=[]
for nm in range(len(MiAvC)):
MiAvD40.append(c.rect(MiAv[nm],Tcode[20]))
MiAvD4=num.array(MiAvD40)
MiBvD40=[]
for nm in range(len(MiBx)):
MiBvD40.append(c.rect(MiBx[nm],Tcode[20]))
MiBvD4=num.array(MiBvD40)
MiCvD40=[]
for nm in range(len(MiHz)):
MiCvD40.append(c.rect(2,Tcode[20]))
MiCvD4=num.array(MiCvD40)
#断面5計算
MiAvD50=[]
for nm in range(len(MiAvC)):
MiAvD50.append(c.rect(MiAv[nm],Tcode[40]))
MiAvD5=num.array(MiAvD20)
MiBvD50=[]
for nm in range(len(MiBx)):
MiBvD50.append(c.rect(MiBx[nm],Tcode[40]))
MiBvD5=num.array(MiBvD50)
MiCvD50=[]
for nm in range(len(MiHz)):
MiCvD50.append(c.rect(2,Tcode[40]))
MiCvD5=num.array(MiCvD50)
#断面6計算
MiAvD60=[]
for nm in range(len(MiAvC)):
MiAvD60.append(c.rect(MiAv[nm],Tcode[50]))
MiAvD6=num.array(MiAvD60)
MiBvD60=[]
for nm in range(len(MiBx)):
MiBvD60.append(c.rect(MiBx[nm],Tcode[50]))
MiBvD6=num.array(MiBvD60)
MiCvD60=[]
for nm in range(len(MiHz)):
MiCvD60.append(c.rect(2,Tcode[50]))
MiCvD6=num.array(MiCvD60)
#軌跡計算
Orb_r=abs(MiAvD[n])
Orb0=[]
for nm in range(len(MiCvD)):
Orb0.append(c.rect(Orb_r,Tcode[nm]))
Orbv=num.array(Orb0)
Orbh=num.repeat(MiAh[n],61)
#円柱描画
ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
#中心線描画
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
#断面1描画
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)
#ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
#断面2描画
ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[-1,-1],color="purple",lw=1)
ax.plot([0,uc[30].real],[0,uc[30].imag],[0,0],color="blue",lw=1)
ax.plot([uc[30].real,MiCvD2[30].real],[uc[30].imag,MiCvD2[30].imag],[0,0],color="purple",lw=1)
ax.plot([uc[30].real,uc[30].real],[uc[30].imag,uc[30].imag],[-1,1],color="purple",lw=1)
#ax.plot([uc[30].real,MiAvD2[30].real],[uc[30].imag,MiAvD2[30].imag],[0,MiAh[30]],color="purple",lw=1)
ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[1,1],color="purple",lw=1)
ax.plot([MiCvD2[30].real,MiCvD2[30].real],[MiCvD2[30].imag,MiCvD2[30].imag],[-1,1],color="purple",lw=1)
ax.plot(MiAvD2.real,MiAvD2.imag,MiAh,color="purple",lw=1)
ax.plot(MiBvD2.real,MiBvD2.imag,MiHz,color="blue",lw=1)
#断面3描画
ax.plot([0,MiCvD3[10].real],[0,MiCvD3[10].imag],[-1,-1],color="purple",lw=1)
ax.plot([0,uc[10].real],[0,uc[10].imag],[0,0],color="blue",lw=1)
ax.plot([uc[10].real,MiCvD3[10].real],[uc[10].imag,MiCvD3[10].imag],[0,0],color="purple",lw=1)
ax.plot([uc[10].real,uc[10].real],[uc[10].imag,uc[10].imag],[-1,1],color="purple",lw=1)
#ax.plot([uc[10].real,MiAvD3[10].real],[uc[10].imag,MiAvD3[10].imag],[0,MiAh[10]],color="purple",lw=1)
ax.plot([0,MiCvD3[10].real],[0,MiCvD3[10].imag],[1,1],color="purple",lw=1)
ax.plot([MiCvD3[10].real,MiCvD3[10].real],[MiCvD3[10].imag,MiCvD3[10].imag],[-1,1],color="purple",lw=1)
ax.plot(MiAvD3.real,MiAvD3.imag,MiAh,color="purple",lw=1)
ax.plot(MiBvD3.real,MiBvD3.imag,MiHz,color="blue",lw=1)
#断面4描画
ax.plot([0,MiCvD4[20].real],[0,MiCvD4[20].imag],[-1,-1],color="green",lw=1)
ax.plot([0,uc[20].real],[0,uc[20].imag],[0,0],color="blue",lw=1)
ax.plot([uc[20].real,MiCvD4[20].real],[uc[20].imag,MiCvD4[20].imag],[0,0],color="green",lw=1)
ax.plot([uc[20].real,uc[20].real],[uc[20].imag,uc[20].imag],[-1,1],color="green",lw=1)
#ax.plot([uc[20].real,MiAvD4[20].real],[uc[20].imag,MiAvD4[20].imag],[0,MiAh[20]],color="green",lw=1)
ax.plot([0,MiCvD4[20].real],[0,MiCvD4[20].imag],[1,1],color="green",lw=1)
ax.plot([MiCvD4[20].real,MiCvD4[20].real],[MiCvD4[20].imag,MiCvD4[20].imag],[-1,1],color="green",lw=1)
ax.plot(MiAvD4.real,MiAvD4.imag,MiAh,color="green",lw=1)
ax.plot(MiBvD4.real,MiBvD4.imag,MiHz,color="blue",lw=1)
#断面5描画
ax.plot([0,MiCvD5[40].real],[0,MiCvD5[40].imag],[-1,-1],color="green",lw=1)
ax.plot([0,uc[40].real],[0,uc[40].imag],[0,0],color="blue",lw=1)
ax.plot([uc[40].real,MiCvD5[40].real],[uc[40].imag,MiCvD5[40].imag],[0,0],color="green",lw=1)
ax.plot([uc[40].real,uc[40].real],[uc[40].imag,uc[40].imag],[-1,1],color="green",lw=1)
#ax.plot([uc[40].real,MiAvD5[40].real],[uc[40].imag,MiAvD5[40].imag],[0,MiAh[40]],color="green",lw=1)
ax.plot([0,MiCvD5[40].real],[0,MiCvD5[40].imag],[1,1],color="green",lw=1)
ax.plot([MiCvD5[40].real,MiCvD5[40].real],[MiCvD5[40].imag,MiCvD5[40].imag],[-1,1],color="green",lw=1)
ax.plot(MiAvD5.real,MiAvD5.imag,MiAh,color="green",lw=1)
ax.plot(MiBvD5.real,MiBvD5.imag,MiHz,color="blue",lw=1)
#断面6描画
ax.plot([0,MiCvD6[50].real],[0,MiCvD6[50].imag],[-1,-1],color="purple",lw=1)
ax.plot([0,uc[50].real],[0,uc[50].imag],[0,0],color="blue",lw=1)
ax.plot([uc[50].real,MiCvD6[50].real],[uc[50].imag,MiCvD6[50].imag],[0,0],color="purple",lw=1)
ax.plot([uc[50].real,uc[50].real],[uc[50].imag,uc[50].imag],[-1,1],color="purple",lw=1)
#ax.plot([uc[50].real,MiAvD6[50].real],[uc[50].imag,MiAvD6[50].imag],[0,MiAh[50]],color="purple",lw=1)
ax.plot([0,MiCvD6[50].real],[0,MiCvD6[50].imag],[1,1],color="purple",lw=1)
ax.plot([MiCvD6[50].real,MiCvD6[50].real],[MiCvD6[50].imag,MiCvD6[50].imag],[-1,1],color="purple",lw=1)
ax.plot(MiAvD6.real,MiAvD6.imag,MiAh,color="purple",lw=1)
ax.plot(MiBvD6.real,MiBvD6.imag,MiHz,color="blue",lw=1)
#軌跡描画
ax.plot(Orbv.real,Orbv.imag,Orbh,color="red",lw=1)
#アニメーション描画
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)
ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="green",lw=1)
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
#アニメーション描画(対蹠)
ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,ucA1[n].real],[0,ucA1[n].imag],[0,0],color="blue",lw=1)
ax.plot([ucA1[n].real,MiFvD[n].real],[ucA1[n].imag,MiFvD[n].imag],[0,0],color="black",lw=1)
ax.plot([ucA1[n].real,ucA1[n].real],[ucA1[n].imag,ucA1[n].imag],[-1,1],color="black",lw=1)
ax.plot([ucA1[n].real,MiDvE[n].real],[ucA1[n].imag,MiDvE[n].imag],[0,MiAh[n]],color="purple",lw=1)
ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiFvD[n].real,MiFvD[n].real],[MiFvD[n].imag,MiFvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiDvD.real,MiDvD.imag,MiAh,color="red",lw=1)
ax.plot(MiEvD.real,MiEvD.imag,MiHz,color="blue",lw=1)
#諸元追加
ax.set_ylim([-2.1,2.1])
ax.set_xlim([-2.1,2.1])
ax.set_zlim([-2.1,2.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elv=25,0で水平,90で垂直)
ax.view_init(elev=25, azim=-45)
# azimにTime_code(n)を設定すると世界の側が回る。
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
# Time_code0=num.arange(0,360,6)
# Time_code=Time_code0[::-1]
# unit_cylinder(15)
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("Torus601.gif", writer="pillow")
四分割トーラス
【Python演算処理】単位トーラスを巡る数理②トーラス群の設定



%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)
# トーラス計算
s2=s1*(1+cv1)
s3=s1*(1-cv1)
# 小半径追加
MiHz0=num.linspace(-1,1,61,endpoint = True)
MiHz=MiHz0[::-1]
MiPx=1+num.sqrt(1-MiHz**2)
MiMx=1-num.sqrt(1-MiHz**2)
MiBx=num.sqrt(1-MiHz**2)
MiHy=num.repeat(0,61)
# 小半径アニメーション(元図形)
MiAh1=num.linspace(-1,1,31,endpoint =True)
MiAh2=num.linspace(-1,1,30,endpoint = False)
MiAh3=num.concatenate([MiAh1, MiAh2[::-1]])
MiAh=num.concatenate([MiAh3[14:61], MiAh3[0:13]])
MiAv1=1-num.sqrt(1-MiAh1**2)
MiAv2=1+num.sqrt(1-MiAh2[::-1]**2)
MiAv3=num.concatenate([MiAv2, MiAv1])
MiAv=num.concatenate([MiAv3[14:61], MiAv3[0:13]])
# 小半径アニメーション(回転)
MiAvC0=[]
for nm in range(len(MiAv)):
MiAvC0.append(complex(MiAv[nm],0))
MiAvC=num.array(MiAvC0)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
Tcode2=num.concatenate([Tcode[30:61], Tcode[0:29]])
Tcode3=num.concatenate([Tcode[15:61], Tcode[0:14]])
Tcode4=num.concatenate([Tcode[45:61], Tcode[0:44]])
# 描画関数定義
def unit_cylinder(n):
plt.cla()
#断面計算(元)
MiAvD0=[]
for nm in range(len(MiAv)):
MiAvD0.append(c.rect(MiAv[nm],Tcode[n]))
MiAvD=num.array(MiAvD0)
MiBvD0=[]
for nm in range(len(MiBx)):
MiBvD0.append(c.rect(MiBx[nm],Tcode[n]))
MiBvD=num.array(MiBvD0)
MiCvD0=[]
for nm in range(len(MiHz)):
MiCvD0.append(c.rect(2,Tcode[n]))
MiCvD=num.array(MiCvD0)
#断面計算(対蹠)
MiDvD0=[]
for nm in range(len(MiAv)):
MiDvD0.append(c.rect(MiAv[nm],Tcode2[n]))
MiDvD=num.array(MiDvD0)
MiDvE=MiDvD[::-1]
MiEvD0=[]
for nm in range(len(MiBx)):
MiEvD0.append(c.rect(MiBx[nm],Tcode2[n]))
MiEvD=num.array(MiEvD0)
MiFvD0=[]
for nm in range(len(MiHz)):
MiFvD0.append(c.rect(2,Tcode2[n]))
MiFvD=num.array(MiFvD0)
ucA1=num.concatenate([uc[30:61], uc[0:29]])
#断面計算(交代)
MiAvDA0=[]
for nm in range(len(MiAv)):
MiAvDA0.append(c.rect(MiAv[nm],Tcode3[n]))
MiAvDA=num.array(MiAvDA0)
MiBvDA0=[]
for nm in range(len(MiBx)):
MiBvDA0.append(c.rect(MiBx[nm],Tcode3[n]))
MiBvDA=num.array(MiBvDA0)
MiCvDA0=[]
for nm in range(len(MiHz)):
MiCvDA0.append(c.rect(2,Tcode3[n]))
MiCvDA=num.array(MiCvDA0)
ucAA=num.concatenate([uc[15:61], uc[0:14]])
#断面計算(交代の対蹠)
MiDvDB0=[]
for nm in range(len(MiAv)):
MiDvDB0.append(c.rect(MiAv[nm],Tcode4[n]))
MiDvDB=num.array(MiDvDB0)
MiDvEB=MiDvDB[::-1]
MiEvDB0=[]
for nm in range(len(MiBx)):
MiEvDB0.append(c.rect(MiBx[nm],Tcode4[n]))
MiEvDB=num.array(MiEvDB0)
MiFvDB0=[]
for nm in range(len(MiHz)):
MiFvDB0.append(c.rect(2,Tcode4[n]))
MiFvDB=num.array(MiFvDB0)
ucAB=num.concatenate([uc[45:61], uc[0:44]])
#断面1計算
MiAvD10=[]
for nm in range(len(MiAvC)):
MiAvD10.append(c.rect(MiAv[nm],Tcode[0]))
MiAvD1=num.array(MiAvD10)
MiBvD10=[]
for nm in range(len(MiBx)):
MiBvD10.append(c.rect(MiBx[nm],Tcode[0]))
MiBvD1=num.array(MiBvD10)
MiCvD10=[]
for nm in range(len(MiHz)):
MiCvD10.append(c.rect(2,Tcode[0]))
MiCvD1=num.array(MiCvD10)
#断面2計算
MiAvD20=[]
for nm in range(len(MiAvC)):
MiAvD20.append(c.rect(MiAv[nm],Tcode[30]))
MiAvD2=num.array(MiAvD20)
MiBvD20=[]
for nm in range(len(MiBx)):
MiBvD20.append(c.rect(MiBx[nm],Tcode[30]))
MiBvD2=num.array(MiBvD20)
MiCvD20=[]
for nm in range(len(MiHz)):
MiCvD20.append(c.rect(2,Tcode[30]))
MiCvD2=num.array(MiCvD20)
#断面3計算
MiAvD30=[]
for nm in range(len(MiAvC)):
MiAvD30.append(c.rect(MiAv[nm],Tcode[15]))
MiAvD3=num.array(MiAvD30)
MiBvD30=[]
for nm in range(len(MiBx)):
MiBvD30.append(c.rect(MiBx[nm],Tcode[15]))
MiBvD3=num.array(MiBvD30)
MiCvD30=[]
for nm in range(len(MiHz)):
MiCvD30.append(c.rect(2,Tcode[15]))
MiCvD3=num.array(MiCvD30)
#断面4計算
MiAvD40=[]
for nm in range(len(MiAvC)):
MiAvD40.append(c.rect(MiAv[nm],Tcode[45]))
MiAvD4=num.array(MiAvD40)
MiBvD40=[]
for nm in range(len(MiBx)):
MiBvD40.append(c.rect(MiBx[nm],Tcode[45]))
MiBvD4=num.array(MiBvD40)
MiCvD40=[]
for nm in range(len(MiHz)):
MiCvD40.append(c.rect(2,Tcode[45]))
MiCvD4=num.array(MiCvD40)
#軌跡計算
Orb_r=abs(MiAvD[n])
Orb0=[]
for nm in range(len(MiCvD)):
Orb0.append(c.rect(Orb_r,Tcode[nm]))
Orbv=num.array(Orb0)
Orbh=num.repeat(MiAh[n],61)
#円柱描画
ax.plot(s2.real,s2.imag,z0,color="gray",lw=0.5)
ax.plot(s3.real,s3.imag,z0,color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
#中心線描画
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
#断面1描画
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[-1,-1],color="green",lw=1)
ax.plot([0,uc[0].real],[0,uc[0].imag],[0,0],color="blue",lw=1)
ax.plot([uc[0].real,MiCvD1[0].real],[uc[0].imag,MiCvD1[0].imag],[0,0],color="green",lw=1)
ax.plot([uc[0].real,uc[0].real],[uc[0].imag,uc[0].imag],[-1,1],color="green",lw=1)
ax.plot([uc[0].real,MiAvD1[0].real],[uc[0].imag,MiAvD1[0].imag],[0,MiAh[0]],color="green",lw=1)
ax.plot([0,MiCvD1[0].real],[0,MiCvD1[0].imag],[1,1],color="green",lw=1)
ax.plot([MiCvD1[0].real,MiCvD1[0].real],[MiCvD1[0].imag,MiCvD1[0].imag],[-1,1],color="green",lw=1)
ax.plot(MiAvD1.real,MiAvD1.imag,MiAh,color="green",lw=1)
ax.plot(MiBvD1.real,MiBvD1.imag,MiHz,color="blue",lw=1)
#断面2描画
ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[-1,-1],color="purple",lw=1)
ax.plot([0,uc[30].real],[0,uc[30].imag],[0,0],color="blue",lw=1)
ax.plot([uc[30].real,MiCvD2[30].real],[uc[30].imag,MiCvD2[30].imag],[0,0],color="purple",lw=1)
ax.plot([uc[30].real,uc[30].real],[uc[30].imag,uc[30].imag],[-1,1],color="purple",lw=1)
ax.plot([uc[30].real,MiAvD2[30].real],[uc[30].imag,MiAvD2[30].imag],[0,MiAh[30]],color="purple",lw=1)
ax.plot([0,MiCvD2[30].real],[0,MiCvD2[30].imag],[1,1],color="purple",lw=1)
ax.plot([MiCvD2[30].real,MiCvD2[30].real],[MiCvD2[30].imag,MiCvD2[30].imag],[-1,1],color="purple",lw=1)
ax.plot(MiAvD2.real,MiAvD2.imag,MiAh,color="purple",lw=1)
ax.plot(MiBvD2.real,MiBvD2.imag,MiHz,color="blue",lw=1)
#断面3描画
ax.plot([0,MiCvD3[15].real],[0,MiCvD3[15].imag],[-1,-1],color="steelblue",lw=1)
ax.plot([0,uc[15].real],[0,uc[15].imag],[0,0],color="blue",lw=1)
ax.plot([uc[15].real,MiCvD3[15].real],[uc[15].imag,MiCvD3[15].imag],[0,0],color="steelblue",lw=1)
ax.plot([uc[15].real,uc[15].real],[uc[15].imag,uc[15].imag],[-1,1],color="steelblue",lw=1)
ax.plot([uc[15].real,MiAvD3[15].real],[uc[15].imag,MiAvD3[15].imag],[0,MiAh[15]],color="steelblue",lw=1)
ax.plot([0,MiCvD3[15].real],[0,MiCvD3[15].imag],[1,1],color="steelblue",lw=1)
ax.plot([MiCvD3[15].real,MiCvD3[15].real],[MiCvD3[15].imag,MiCvD3[15].imag],[-1,1],color="steelblue",lw=1)
ax.plot(MiAvD3.real,MiAvD3.imag,MiAh,color="steelblue",lw=1)
ax.plot(MiBvD3.real,MiBvD3.imag,MiHz,color="blue",lw=1)
#断面4描画
ax.plot([0,MiCvD4[45].real],[0,MiCvD4[45].imag],[-1,-1],color="salmon",lw=1)
ax.plot([0,uc[45].real],[0,uc[45].imag],[0,0],color="blue",lw=1)
ax.plot([uc[45].real,MiCvD4[45].real],[uc[45].imag,MiCvD4[45].imag],[0,0],color="salmon",lw=1)
ax.plot([uc[45].real,uc[45].real],[uc[45].imag,uc[45].imag],[-1,1],color="salmon",lw=1)
ax.plot([uc[45].real,MiAvD4[45].real],[uc[45].imag,MiAvD4[45].imag],[0,MiAh[45]],color="salmon",lw=1)
ax.plot([0,MiCvD4[45].real],[0,MiCvD4[45].imag],[1,1],color="salmon",lw=1)
ax.plot([MiCvD4[45].real,MiCvD4[45].real],[MiCvD4[45].imag,MiCvD4[45].imag],[-1,1],color="salmon",lw=1)
ax.plot(MiAvD4.real,MiAvD4.imag,MiAh,color="salmon",lw=1)
ax.plot(MiBvD4.real,MiBvD4.imag,MiHz,color="blue",lw=1)
#アニメーション描画
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,uc[n].real],[0,uc[n].imag],[0,0],color="blue",lw=1)
ax.plot([uc[n].real,MiCvD[n].real],[uc[n].imag,MiCvD[n].imag],[0,0],color="black",lw=1)
ax.plot([uc[n].real,uc[n].real],[uc[n].imag,uc[n].imag],[-1,1],color="black",lw=1)
ax.plot([uc[n].real,MiAvD[n].real],[uc[n].imag,MiAvD[n].imag],[0,MiAh[n]],color="green",lw=1)
ax.plot([0,MiCvD[n].real],[0,MiCvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiCvD[n].real,MiCvD[n].real],[MiCvD[n].imag,MiCvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiAvD.real,MiAvD.imag,MiAh,color="red",lw=1)
#ax.plot(MiBvD.real,MiBvD.imag,MiHz,color="blue",lw=1)
#アニメーション描画(対蹠)
ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,ucA1[n].real],[0,ucA1[n].imag],[0,0],color="blue",lw=1)
ax.plot([ucA1[n].real,MiFvD[n].real],[ucA1[n].imag,MiFvD[n].imag],[0,0],color="black",lw=1)
ax.plot([ucA1[n].real,ucA1[n].real],[ucA1[n].imag,ucA1[n].imag],[-1,1],color="black",lw=1)
ax.plot([ucA1[n].real,MiDvE[n].real],[ucA1[n].imag,MiDvE[n].imag],[0,MiAh[n]],color="purple",lw=1)
ax.plot([0,MiFvD[n].real],[0,MiFvD[n].imag],[1,1],color="black",lw=1)
ax.plot([MiFvD[n].real,MiFvD[n].real],[MiFvD[n].imag,MiFvD[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiDvD.real,MiDvD.imag,MiAh,color="red",lw=1)
ax.plot(MiEvD.real,MiEvD.imag,MiHz,color="blue",lw=1)
#アニメーション描画(交代)
ax.plot([0,MiCvDA[n].real],[0,MiCvDA[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,ucAA[n].real],[0,ucAA[n].imag],[0,0],color="blue",lw=1)
ax.plot([ucAA[n].real,MiCvDA[n].real],[ucAA[n].imag,MiCvDA[n].imag],[0,0],color="black",lw=1)
ax.plot([ucAA[n].real,ucAA[n].real],[ucAA[n].imag,ucAA[n].imag],[-1,1],color="black",lw=1)
ax.plot([ucAA[n].real,MiAvDA[n].real],[ucAA[n].imag,MiAvDA[n].imag],[0,MiAh[n]],color="steelblue",lw=1)
ax.plot([0,MiCvDA[n].real],[0,MiCvDA[n].imag],[1,1],color="black",lw=1)
ax.plot([MiCvDA[n].real,MiCvDA[n].real],[MiCvDA[n].imag,MiCvDA[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiAvDA.real,MiAvDA.imag,MiAh,color="red",lw=1)
ax.plot(MiBvDA.real,MiBvDA.imag,MiHz,color="blue",lw=1)
#アニメーション描画(交代の対蹠)
ax.plot([0,MiFvDB[n].real],[0,MiFvDB[n].imag],[-1,-1],color="black",lw=1)
ax.plot([0,ucAB[n].real],[0,ucAB[n].imag],[0,0],color="blue",lw=1)
ax.plot([ucAB[n].real,MiFvDB[n].real],[ucAB[n].imag,MiFvDB[n].imag],[0,0],color="black",lw=1)
ax.plot([ucAB[n].real,ucAB[n].real],[ucAB[n].imag,ucAB[n].imag],[-1,1],color="black",lw=1)
ax.plot([ucAB[n].real,MiDvEB[n].real],[ucAB[n].imag,MiDvEB[n].imag],[0,MiAh[n]],color="salmon",lw=1)
ax.plot([0,MiFvDB[n].real],[0,MiFvDB[n].imag],[1,1],color="black",lw=1)
ax.plot([MiFvDB[n].real,MiFvDB[n].real],[MiFvDB[n].imag,MiFvDB[n].imag],[-1,1],color="black",lw=1)
ax.plot(MiDvDB.real,MiDvDB.imag,MiAh,color="red",lw=1)
ax.plot(MiEvDB.real,MiEvDB.imag,MiHz,color="blue",lw=1)
#軌跡描画
ax.plot(Orbv.real,Orbv.imag,Orbh,color="red",lw=1)
#諸元追加
ax.set_ylim([-2.1,2.1])
ax.set_xlim([-2.1,2.1])
ax.set_zlim([-2.1,2.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転(elv=25,0で水平,90で垂直)
ax.view_init(elev=25, azim=-45)
Tcode=num.linspace(0,m.pi*2,61,endpoint =True)
# azimにTime_code(n)を設定すると世界の側が回る。
# Time_code0=num.arange(0,360,6)
# Time_code=Time_code0[::-1]
# unit_cylinder(15)
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("torus401.gif", writer="pillow")
【Python演算処理】単位球面を巡る数理②そして単位トーラスへ
大半径(Major Radius)Rと小半径(Minor Radius)の組み合わせで表現されるトーラス座標系(Torus Coordinates System)とデカルト座標系の関係は、一般に媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表されます。
- x=$R×\cos(t)+r×\cos(p)\cos(t)$
- y=$R×cos(t)+r×\cos(p)\sin(t)$
- z=$r×\sin(p)$
- 表面積$S=4π^2rR=(2πr)(2πR)$
- 体積$V=2π^2r^2R=(πr^2)(2πR)$
上掲の円/球面座標系との関係は以下となります。
- 大半径R=0,小半径r=1の時、単位球面(Unit Sphere)を二重に描く。従って経緯度法(経度-180度→+180度に対して緯度-90度→+90度)や3次元極座標系(水平角φ=-π→+πに対して垂直角θ=0→π)は適用範囲を半分に減らしてなお単位球面(Unit Sphere)上の全座標を示せる訳である。
- 逆に大半径R=1,小半径r=0の時、Z=0となってただの単位円(Unit Circle)となる。大半径Rと小半径rの比が1:1の場合(外径が半径1の単位円と一致するのは大半径R=小半径r=$\frac{1}{2}$の時で、大半径R=小半径r=1の時の外径は2となる)からこの極限状態に向かう展開は「半径1の単位円に内接する正N角形とそのさらなる内接円の推移($N=\infty$に近づくほど、その正N角形の辺長計は円周長2πに限りなく近づく)」数理そのものである。
【初心者向け】挟み撃ち定理による円周率πの近似
import sympy as sp
import numpy as np
from sympy import I, pi, E
x,y,z,r,R,p,t,S,V= sp.symbols('x,y,z,R,r,p,t,S,V')
# トーラス座標系(R,t)(r,p)からデカルト座標系(x,y,z)への変換
eq01=sp.Eq(x,R*sp.cos(t)+r*sp.cos(p)*sp.cos(t))
eq02=sp.Eq(y,R*sp.sin(t)+r*sp.cos(p)*sp.sin(t))
eq03=sp.Eq(z,r*sp.sin(p))
eq04=sp.Eq(S,4*pi**2*r*R)
eq05=sp.Eq(S,(2*pi*r)*(2*pi*R))
eq06=sp.Eq(V,2*pi**2*r**2*R)
eq07=sp.Eq(V,(pi*r**2)*(2*pi*R))
# 大半径R=0,小半径r=1の時
eq11=eq01.subs([(r,1),(R,0)])
eq12=eq02.subs([(r,1),(R,0)])
eq13=eq03.subs([(r,1),(R,0)])
eq14=eq04.subs([(r,1),(R,0)])
eq15=eq05.subs([(r,1),(R,0)])
eq16=eq06.subs([(r,1),(R,0)])
eq17=eq07.subs([(r,1),(R,0)])
# 大半径R=1,小半径r=0の時
eq21=eq01.subs([(r,0),(R,1)])
eq22=eq02.subs([(r,0),(R,1)])
eq23=eq03.subs([(r,0),(R,1)])
eq24=eq04.subs([(r,0),(R,1)])
eq25=eq05.subs([(r,0),(R,1)])
eq26=eq06.subs([(r,0),(R,1)])
eq27=eq07.subs([(r,0),(R,1)])
# 大半径R=1,小半径r=1の時
eq31=eq01.subs([(r,1),(R,1)])
eq32=eq02.subs([(r,1),(R,1)])
eq33=eq03.subs([(r,1),(R,1)])
eq34=eq04.subs([(r,1),(R,1)])
eq35=eq05.subs([(r,1),(R,1)])
eq36=eq06.subs([(r,1),(R,1)])
eq37=eq07.subs([(r,1),(R,1)])
# tex
sp.init_printing()
print("トーラス座標系(R,t)(r,p)からデカルト座標系(x,y,z)への変換")
display(eq01)
print(sp.latex(eq01))
display(eq02)
print(sp.latex(eq02))
display(eq03)
print(sp.latex(eq03))
display(eq04)
print(sp.latex(eq04))
display(eq05)
print(sp.latex(eq05))
display(eq06)
print(sp.latex(eq06))
display(eq07)
print(sp.latex(eq07))
print("大半径R=0,小半径r=1の時")
display(eq11)
print(sp.latex(eq11))
display(eq12)
print(sp.latex(eq12))
display(eq13)
print(sp.latex(eq13))
display(eq14)
print(sp.latex(eq14))
display(eq15)
print(sp.latex(eq15))
display(eq16)
print(sp.latex(eq16))
display(eq17)
print(sp.latex(eq17))
print("大半径R=1,小半径r=0の時")
display(eq21)
print(sp.latex(eq21))
display(eq22)
print(sp.latex(eq22))
display(eq23)
print(sp.latex(eq23))
display(eq24)
print(sp.latex(eq24))
display(eq25)
print(sp.latex(eq25))
display(eq26)
print(sp.latex(eq26))
display(eq27)
print(sp.latex(eq27))
print("大半径R=1,小半径r=1の時")
display(eq31)
print(sp.latex(eq31))
display(eq32)
print(sp.latex(eq32))
display(eq33)
print(sp.latex(eq33))
display(eq34)
print(sp.latex(eq34))
display(eq35)
print(sp.latex(eq35))
display(eq36)
print(sp.latex(eq36))
display(eq37)
print(sp.latex(eq37))
トーラス座標系(R,t)(r,p)からデカルト座標系(x,y,z)への変換
\begin{align*}
&x = R \cos{\left(p \right)} \cos{\left(t \right)} + r \cos{\left(t \right)}\\
&y = R \sin{\left(t \right)} \cos{\left(p \right)} + r \sin{\left(t \right)}\\
&z = R \sin{\left(p \right)}\\
&S = 4 \pi^{2} R r\\
&V = 2 \pi^{2} R^{2} r
\end{align*}
大半径R=0,小半径r=1の場合
\begin{align*}
&x = \cos{\left(p \right)} \cos{\left(t \right)}\\
&y = \sin{\left(t \right)} \cos{\left(p \right)}\\
&z = \sin{\left(p \right)}
\end{align*}
- 大半径Rに直交する小半径rがらみの演算だけが残り、三次元極座標系r(φ,θ)を90度回転させた様な式に従う半径1の単位球面が現れる。rの範囲は2π(0~2πあるいは-π~π)なので三次元極座標系や緯度経度法の考え方を援用しても「2個分ある」。
- ちなみに2πR=0なので表面積も体積も0。rR比概念では到達不可能な極限状態の一つ。
大半径R=1,小半径r=0の場合
\begin{align*}
&x = \cos{\left(t \right)}\\
&y = \sin{\left(t \right)}\\
&z = 0
\end{align*}
- 大半径Rがらみの演算だけが残り、二次元極座標系r(φ)に従う半径1の単位円(高さ0)が現れる。
- やはり2πr=0なので表面積も体積も0。rR比概念では到達不可能な極限状態のもう一つ。
大半径R=1,小半径r=1の場合(単位トーラス)
\begin{align*}
&x = \cos{\left(p \right)} \cos{\left(t \right)} + \cos{\left(t \right)}\\
&y = \sin{\left(t \right)} \cos{\left(p \right)} + \sin{\left(t \right)}\\
&z = \sin{\left(p \right)}\\
&S = 2π*2π =4 \pi^{2}\\
&V = π*2π = 2 \pi^{2}
\end{align*}
トーラスの表面積は底面が半径rで高さが2πRの円柱の側面積に等しく、体積はその円柱と同値となる。
まさしくこれこそが虚数冪(Imaginal Exponentiation)$e^{iθ}$の世界(それにつけても突如として自明の場合として割り込んでくる虚数i概念!!)。
【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式
- $\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}$
- $\sin(θ)=\frac{e^{θi}-e^{-θi}}{2i}$
- $e^{ix}\frac{d^n}{dθ^n}=(i e^{i x}(-\log ix),-e^{ix},-i e^{i x}(\log ix),e^{ix},…)$
- $\int \int \int … \int e^{ix}(dθ)=(- i e^{i x}(\log ix),- e^{i x},i e^{i x}(-\log ix),e^{ix},…)$
しかしながらこの式はその本来の限界たる観測原点0に差し掛かっていて、虚数(Imaginal)の概念を導入しないのなら、例えば冪乗算の定積分たる以下の式でβ=-1の時、分母が0になり計算不能となってしまいます。
【数理考古学】冪乗算の微積分
{\int_{a}^{b}f(x)dx\\
=(\frac{1}{β+1}b^{β+1}+C)-(\frac{1}{β+1}a^{β+1}+C)\\
=\frac{1}{β+1}b^{β+1}-\frac{1}{β+1}a^{β+1}
}
β=-1の時(計算自体は途中で座説するが、考え方としてはこう)
{\int_{a}^{b}f(x)dx\\
=(\frac{1}{0}b^{0}+C)-(\frac{1}{0}a^{0}+C)\\
=\frac{1}{0}b^{0}-\frac{1}{0}a^{0}\\
=\frac{1}{0}-\frac{1}{0}=0}
計算的には$\int_{1}^{2}\frac{1}{x}dx$すなわち反比例関数$y=\frac{1}{x}$における区間1→2の定積分を求める場合と一致する。
そこで数学の世界は以下の方便を採用する事に決めたのです。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数
2の冪乗算$f(x)=2^x=e^{n\log{2}}$と「0から2までの正の実数」の組み合わせは任意の正の実数を表せる。
2^n(n=-\infty→+\infty)=(2^{-\infty}=\frac{1}{\infty}=0,…,2^{-2}=\frac{1}{2^2}=\frac{1}{4},…,2^{-1}=\frac{1}{2},…,2^0=\frac{2}{2}=1,…,2^1=2,…,2^2=4,…,2^{+\infty}=\infty)
| Values | Explessions | |
|---|---|---|
| 1 | 1 | 2^0 |
| 2 | 2 | 2^1 |
| 3 | 3 | 2^0+2^1 / 2^log(3,base=2) |
| 4 | 4 | 2^2 |
| 5 | 5 | 2^2+2^0 |
| 6 | 6 | 2^2+2^1 |
| 7 | 7 | 2^2+2^log(3,base=2) |
| 8 | 8 | 2^3 |
その対数写像、すなわち「0から2までの正の実数」と$\log2$概念を組み合わせは任意の正の対数を表せる。
| Numbers | Explessions | Values | |
|---|---|---|---|
| 1 | log(1) | log(2^1)+log(1/2) | 0 |
| 2 | log(2) | log(2^1) | 0.6931472 |
| 3 | log(3) | log(3/2)+log(2^1) | 1.098612 |
| 4 | log(4) | log(2^2) | 1.386294 |
| 5 | log(5) | log(5/4)+log(2^2) | 1.609438 |
| 6 | log(6) | log(3/2)+log(2^2) | 1.791759 |
| 7 | log(7) | log(7/4)+log(2^2) | 1.94591 |
| 8 | log(8) | log(2^3) | 2.079442 |
こう考えるなら、$\log{2}(0.6931472)$をあらかじめ計算しておく事で、全ての実数と指数を表す事が出来る様になる。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?
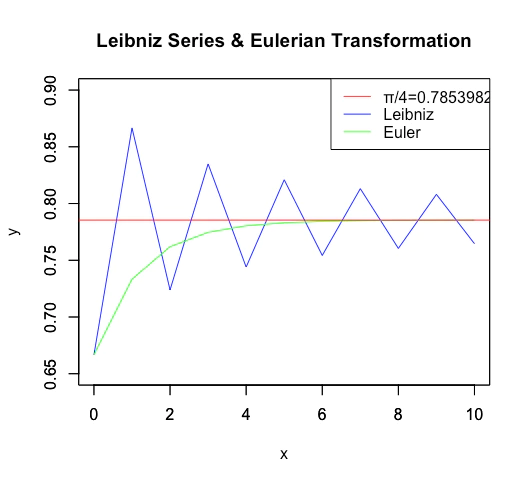
- そして特殊直交行列(Special Orthogonal Matrix)においては半径1の単位円をSO(2),半径1の単位球面をSO(3)と表記する。一方リー群論(Lee Group Theory)においては同じ半径1の単位円を1次元トーラス$S_0$と規定し、上掲の単位トーラスを2次元トーラス$S_1$、さらに原点を中心に回転する小半径円盤(回転軸i)に回転軸j,kを加えた四元数座標系(Quaternion Coordinate System)を3次元トーラス$S_3$と呼ぶ(おそらく結論からいえばたったこれだけの事の様なのだが、素直にそう記述している説明に邂逅出来ず、全体イメージをこういう形にまとめるのに数ヶ月を要し、なおかつ現時点でそれが正解かわからない)。
【数理考古学】群論とシミュレーション原理⑦三次元トーラスとしての四元数概念導入
ここまで考え抜いてやっと群としても考えられる乗法的同心円/球面集合の全体像が浮かび上がってくる訳です。
乗法的同心群(Multiplicative Concentric Group)
ところで上掲の乗法的同心集合は乗法群(Multiplicative Group)としての基準も満たしてはいるのです。
【数理考古学】群論概念①基本定義
- 積もまた集合の要素になっていること…全てが実数列の領域で展開する訳だから、これは自明の場合(Trival Case)となる。
- 結合法則が成り立つこと…実数列を添字とする添字集合(Index Set)として成立しているのだから、これも自明の場合となる。
- 逆元が存在すること…同上
- 単位元が存在する事…全体が乗法単位元1を中心に展開している。
なので以降はこれを乗法的同心群(Multiplicative Concentric Group)とも呼んでいこうと思います。
以下に続きます。
【Pyrhon演算処理】同心集合②加法的同心集合とは?










