【オイラーの多面体定理と正多面体】二次元上の多角形と三次元上の多面体の往復

【Rで球面幾何学】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)


ここで紹介した正十二面体(Dodecahedron)における「屋根掛け法(Roofing method)」の概念は案外、他の図形にも応用出来たりするのです。

##【3^n集と2^n3^m集の往復】正三角形(Triangle)と正六角形(Hexagon)の間の平方双対変換(Square Dual Transform)

直接「屋根掛け法」自体には関係しませんが、全体像を俯瞰するのに必要不可欠なので一応紹介しておきます。正三角形は各頂点より２辺ずつ伸ばした合計6辺を結ぶと自己相似図形を再構成するのです。

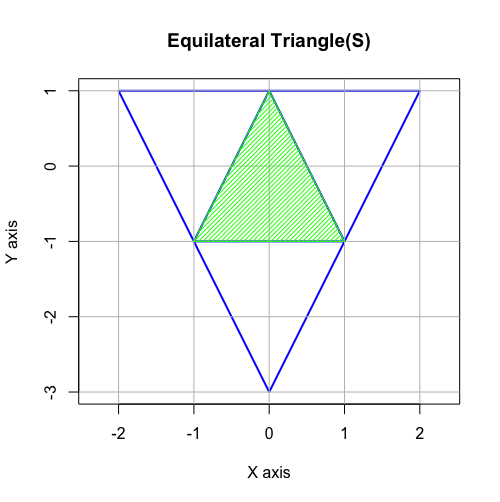
#Equilateral Triangle(S) 
cx=c(-2,2,0,-2)
cy=c(1,1,-3,1)
plot(cx,cy,type="l",asp=1,xlim=c(-2,2),ylim=c(-3,1),col=rgb(0,0,1),lwd=2, main="Equilateral Triangle(S)",xlab="X axis",ylab="Y axis")

lines(c(-1,0), c(-1,1),col=rgb(0,0,1),lwd=2)
lines(c(0,1), c(1,-1),col=rgb(0,0,1),lwd=2)
lines(c(-1,1), c(-1,-1),col=rgb(0,0,1),lwd=2)                        

#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
 }                             

#三角形塗り潰し
polygon(c(-1,0,1,-1), #x
c(-1,1,-1,-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

その平面充填(Tiling)に際しては、奇数の階差数列単位でこれが繰り返されるのです。一方向に伸びていくイメージ。

#階差数列の導出
> c0<-c(0,1,4,9,16,25,36)
> diff(c0)
[1]  1  3  5  7  9 11

#一般項
f0<-function(x){
d<-0
for(i in 0:x){
d<-d+2*i+1
}
return(d)
}
>c(f0(0),f0(1),f0(2),f0(3),f0(4),f0(5))
[1]  1  4  9 16 25 36

この様に「中心面より各頂点より２辺ずつ伸ばした合計6辺を結ぶと相似形を再構成する」正三角形に平方双対変換(Square Dual Transform)を加えると「中心点より6辺を伸ばした」正六角形となります。

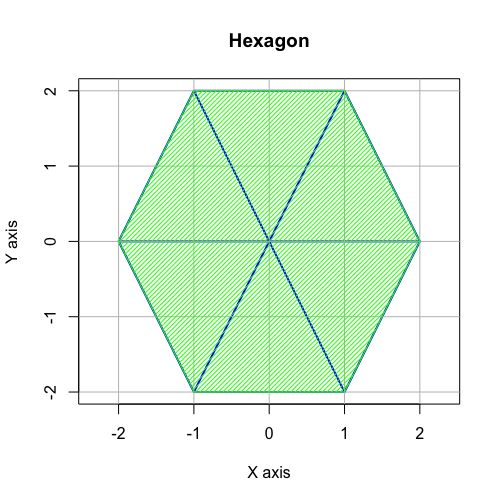
#Hexagon 
cx=c(-2,-1,1,2,1,-1,-2)
cy=c(0,2,2,0,-2,-2,0)
plot(cx,cy,type="l",asp=1,xlim=c(-2,2),ylim=c(-2,2),col=rgb(0,0,1),lwd=2, main="Hexagon",xlab="X axis",ylab="Y axis")

lines(c(-1,1), c(-2,2),col=rgb(0,0,1),lwd=2)
lines(c(-1,1), c(2,-2),col=rgb(0,0,1),lwd=2)                        
lines(c(-2,2), c(0,0),col=rgb(0,0,1),lwd=2)                        

#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
}                             

#六角形塗り潰し
polygon(c(-2,-1,1,2,1,-1,-2), #x
c(0,2,2,0,-2,-2,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

その平面充填(Tiling)に際してはもはや自己相似型は現れず、距離に対して初項1,6の倍数を階差数列単位で構成数が増加していきます。六方に広がっていくイメージ。

#階差数列の導出
> c0<-c(1,7,19,37,61,91)
> diff(c0)
[1]  6 12 18 24 30

#一般項
f0<-function(x){
d<-1
for(i in 0:x){
d<-d+6*i
}
return(d)
}
>c(f0(0),f0(1),f0(2),f0(3),f0(4),f0(5))
[1]  1  7 19 37 61 91

ところで整数倍の平方眼(Square Grid)を意識したこの図示は正六角形(Regurar Hexagon)をちゃんと描いていません。逆にかかる変遷において正六角形を描こうとするなら平方眼に収まらないのです。正三角形が平面充填性は備えつつ、立体充填性(Space Filling)までは備えていないであろう事は、この辺りからも推察可能という次第。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

##【2^n集と2^n3^m集の往復】正方形(Square)と正八面体(Octahedron)の往復

以下の投稿では「オイラーの多角形定理は、平面上では頂点(Vertex)の数－辺(Edge)の数＝0もしくは頂点(Vertex)の数－辺(Edge)の数＋面(Face)の数＝1となる」としました。
【オイラーの多面体定理と正多面体】「オイラーの多角形定理」と「意味論的統制」概念の導入

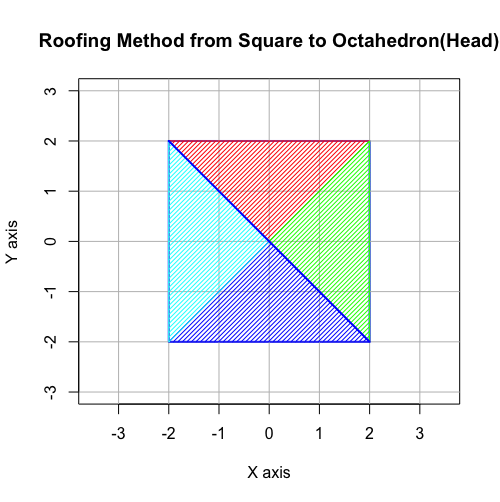
逆を言えばXY軸上の正方形における平方対角線(Square Diagonal)２本の交点に原蹠(Portal)と対蹠(Antipordal)の2点を加えて表裏(Head-Tail)の概念を導入しZ軸上に展開する同じ長さの3本目の平方対角線を加えたのが正八面体という事になります。とりあえずこの変換においては「表(Head)」側の「屋根掛け」と「裏(Tail)」の「屋根掛け」が完全に一致…

###「表(Head)」側の「屋根掛け」

#Roofing Method from Square to Octahedron(Head) 
cx=c(-2,2,2,-2,-2)
cy=c(-2,-2,2,2,-2)
plot(cx,cy,type="l",asp=1,xlim=c(-3,3),ylim=c(-3,3),col=rgb(0,0,1),lwd=2, main="Roofing Method from Square to Octahedron(Head)",xlab="X axis",ylab="Y axis")

#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
 } 

#三角形１(赤)
polygon(c(-2,2,0,-2), #x
c(2,2,0,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#三角形2(緑)
polygon(c(2,2,0,2), #x
c(2,-2,0,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#三角形3(青)
polygon(c(2,0,-2,2), #x
c(-2,0,-2,-2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#三角形4(水色)
polygon(c(-2,0,-2,-2), #x
c(2,0,-2,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,1)) 　#塗りつぶす色

lines(c(-2,2), c(2,-2),col=rgb(0,0,1),lwd=2)
lines(c(-2,-2), c(2,2),col=rgb(0,0,1),lwd=2)

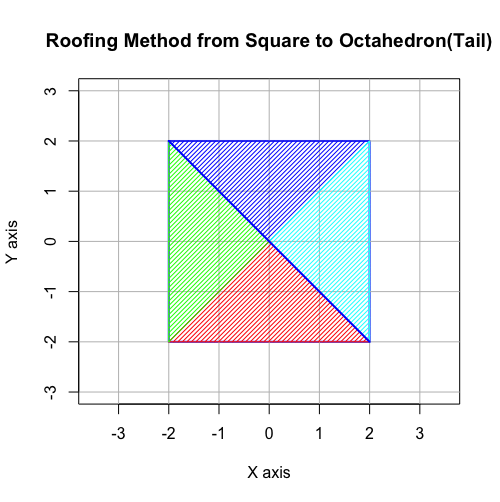
###「裏(Tail)」側の「屋根掛け」

#Roofing Method from Square to Octahedron(Tail) 
cx=c(-2,2,2,-2,-2)
cy=c(-2,-2,2,2,-2)
plot(cx,cy,type="l",asp=1,xlim=c(-3,3),ylim=c(-3,3),col=rgb(0,0,1),lwd=2, main="Roofing Method from Square to Octahedron(Tail)",xlab="X axis",ylab="Y axis")

#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
 } 

#三角形１(青)
polygon(c(-2,2,0,-2), #x
c(2,2,0,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#三角形2(水色)
polygon(c(2,2,0,2), #x
c(2,-2,0,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,1)) 　#塗りつぶす色

#三角形3(赤)
polygon(c(2,0,-2,2), #x
c(-2,0,-2,-2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#三角形4(緑)
polygon(c(-2,0,-2,-2), #x
c(2,0,-2,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

lines(c(-2,2), c(2,-2),col=rgb(0,0,1),lwd=2)
lines(c(-2,-2), c(2,2),col=rgb(0,0,1),lwd=2)

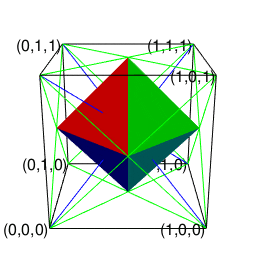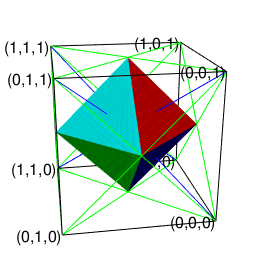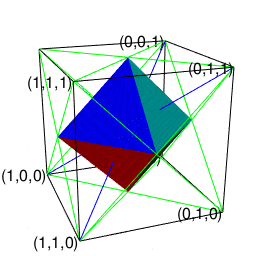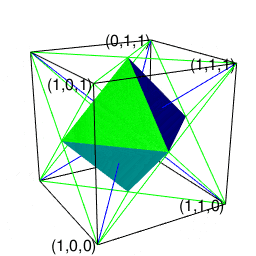
###変換結果

library(rgl)
#頂点座標=8個
texts3d(0,0,0,texts=c("(0,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,0,texts=c("(0,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,0,texts=c("(1,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,0,1,texts=c("(0,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,1,texts=c("(1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,1,texts=c("(0,1,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,1,texts=c("(1,1,1)"),col=rgb(0,0,0),adj=1.0)
#正六面体(Square)本体=6面

lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(0,0,0,0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(1,1,1,1,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)

#平方対角線(長さsqrt(2))=6面*2=12本
lines3d(c(0,1),c(0,1),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,1),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(0,1),col=rgb(0,1,0),lwd=1)

#立方対角線(長さsqrt(3))=3本

lines3d(c(0,1),c(0,1),c(0,1),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(1,0),c(1,0),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(0,1),c(1,0),col=rgb(0,0,1),lwd=1)

#正八面体(1辺sqrt(2))
triangles3d(c(1,1/2,1/2),c(1/2,1,1/2),c(1/2,1/2,0),col=rgb(1,0,0),lwd=1)
triangles3d(c(1/2,0,1/2),c(1,1/2,1/2),c(1/2,1/2,0),col=rgb(0,1,0),lwd=1)
triangles3d(c(0,1/2,1/2),c(1/2,0,1/2),c(1/2,1/2,0),col=rgb(0,0,1),lwd=1)
triangles3d(c(1/2,1,1/2),c(0,1/2,1/2),c(1/2,1/2,0),col=rgb(0,1,1),lwd=1)

triangles3d(c(1,1/2,1/2),c(1/2,1,1/2),c(1/2,1/2,1),col=rgb(0,0,1),lwd=1)
triangles3d(c(1/2,0,1/2),c(1,1/2,1/2),c(1/2,1/2,1),col=rgb(0,1,1),lwd=1)
triangles3d(c(0,1/2,1/2),c(1/2,0,1/2),c(1/2,1/2,1),col=rgb(1,0,0),lwd=1)
triangles3d(c(1/2,1,1/2),c(0,1/2,1/2),c(1/2,1/2,1),col=rgb(0,1,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/triangles005") 

ある意味、正三角形を中心と各頂点で結ぶ線で三分割し、中心に原蹠(Portal)と対蹠(Antipordal)を結ぶZ軸上の2点を加えて表裏(Head-Tail)の概念を導入し正四面体２個を発生させる(ただしそれ自体は正多面体の範疇に含まれない)変換の拡張版といえましょう。ただしこちらの変換の方が「(主にXYZ軸上の整数倍の目盛りにのみ注目し)平方対角線sqrt(2)の存在をほぼ黙殺し得る(立方対角線sqrt(3)の概念に至っては登場すらしない)」という点において人間が直感的に把握可能な空間認識能力上は遥かに扱いやすいのです。
【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。

その一方で正八面体もまた単体では空間充填性を備えず、正四面体による補完を必要とします。逆をいえば(整数倍の平方眼上で自然に扱え、平面充填性も備える)正方形や正三角形から変換可能な正多面体で、なおかつ単体で空間充填性も(それも原則として整数と平方対角線sqrt(2)/立方対角線sqrt(3)に尺度の大部分を頼る平方眼/立方眼上で自然に扱える形で!!)備えるのは本当に立方体しかないのです。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

##【2^n3^m集内の変換】六角形(Hexagon)と立方体(Cube)の往復

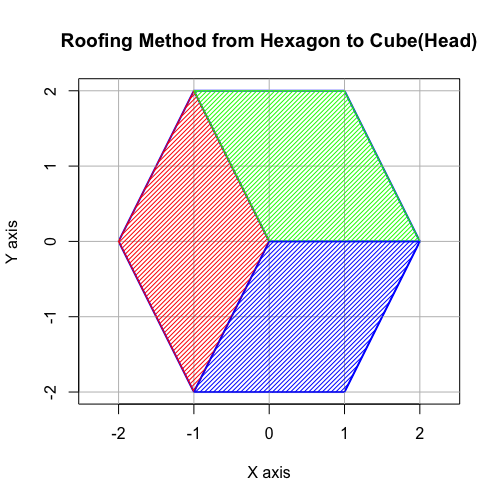
まずは正六面体からの変換について説明します。この変換では「表(Head)」側の「屋根掛け」と「裏(Tail)」側の「屋根掛け」を反転させないといけません。

###「表(Head)」側の「屋根掛け」

#Roofing Method from Hexagon to Cube(Head)
cx=c(-2,-1,1,2,1,-1,-2)
cy=c(0,2,2,0,-2,-2,0)
plot(cx,cy,type="l",asp=1,xlim=c(-2,2),ylim=c(-2,2),col=rgb(0,0,1),lwd=2, main="Roofing Method from Hexagon to Cube(Head)",xlab="X axis",ylab="Y axis")

lines(c(-1,0), c(-2,0),col=rgb(0,0,1),lwd=2)
lines(c(-1,0), c(2,0),col=rgb(0,0,1),lwd=2)                        
lines(c(0,2), c(0,0),col=rgb(0,0,1),lwd=2)                        

#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
 }   

#菱形１
polygon(c(-2,-1,0,-1,-2), #x
c(0,2,0,-2,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#菱形2
polygon(c(-1,1,2,0,-1), #x
c(2,2,0,0,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#菱形3
polygon(c(-1,0,2,1,-1), #x
c(-2,0,0,-2,-2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

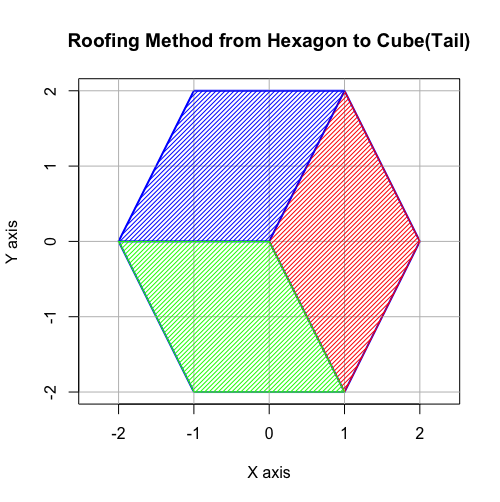
###「裏(Tail)」側の「屋根掛け」

#Roofing Method from Hexagon to Cube(Tail)
cx=c(-2,-1,1,2,1,-1,-2)
cy=c(0,2,2,0,-2,-2,0)
plot(cx,cy,type="l",asp=1,xlim=c(-2,2),ylim=c(-2,2),col=rgb(0,0,1),lwd=2, main="Roofing Method from Hexagon to Cube(Tail)",xlab="X axis",ylab="Y axis")

lines(c(1,0), c(2,0),col=rgb(0,0,1),lwd=2)
lines(c(1,0), c(-2,0),col=rgb(0,0,1),lwd=2)                        
lines(c(0,-2), c(0,0),col=rgb(0,0,1),lwd=2)                        

#方眼(Square Grid)
for (i in -5:5) {
abline(h = i,col=c(200,200,200))
abline(v = i,col=c(200,200,200))
 }   

#菱形１
polygon(c(2,1,0,1,2), #x
c(0,2,0,-2,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#菱形2
polygon(c(1,0,-2,-1,1), #x
c(2,0,0,2,2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#菱形3
polygon(c(1,-1,-2,0,1), #x
c(-2,-2,0,0,-2), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

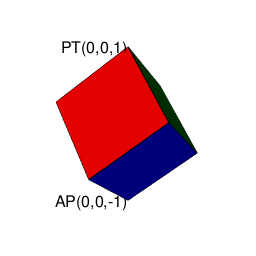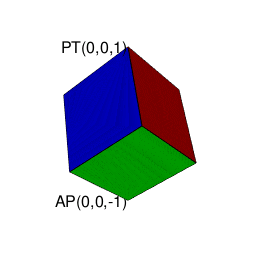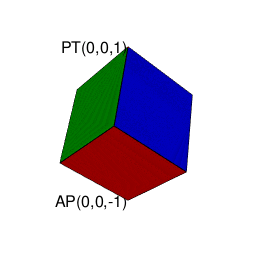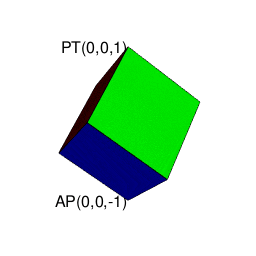
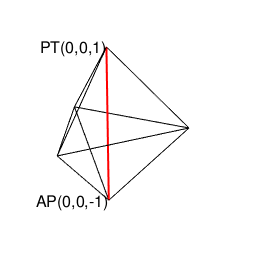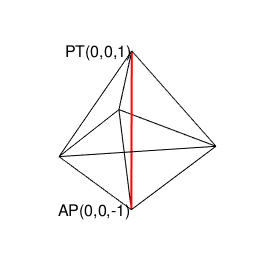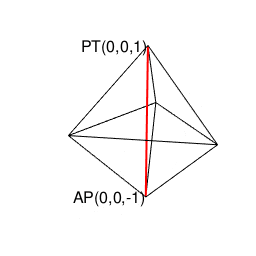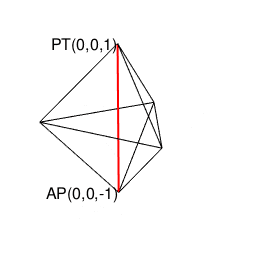
###操作結果

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#立方体面描画(赤)
x1<-c(portal_i, LN01_cos[1], LN02_cos[2],LN01_cos[3])
y1<-c(portal_j, LN01_sin[1], LN02_sin[2],LN01_sin[3])
z1<-c(portal_k,AP01,AP02,AP01)
quads3d(x1,y1,z1,color=rgb(1,0,0))

x2<-c(antipordal_i, LN02_cos[1], LN01_cos[2],LN02_cos[3])
y2<-c(antipordal_j, LN02_sin[1], LN01_sin[2],LN02_sin[3])
z2<-c(antipordal_k,AP02,AP01,AP02)
quads3d(x2,y2,z2,color=rgb(1,0,0))

#立方体面描画(緑)
x1<-c(portal_i, LN01_cos[2], LN02_cos[3],LN01_cos[1])
y1<-c(portal_j, LN01_sin[2], LN02_sin[3],LN01_sin[1])
z1<-c(portal_k,AP01,AP02,AP01)
quads3d(x1,y1,z1,color=rgb(0,1,0))

x2<-c(antipordal_i, LN02_cos[2], LN01_cos[3],LN02_cos[1])
y2<-c(antipordal_j, LN02_sin[2], LN01_sin[3],LN02_sin[1])
z2<-c(antipordal_k,AP02,AP01,AP02)
quads3d(x2,y2,z2,color=rgb(0,1,0))

#立方体面描画(青)
x1<-c(portal_i, LN01_cos[3], LN02_cos[1],LN01_cos[2])
y1<-c(portal_j, LN01_sin[3], LN02_sin[1],LN01_sin[2])
z1<-c(portal_k,AP01,AP02,AP01)
quads3d(x1,y1,z1,color=rgb(0,0,1))

x2<-c(antipordal_i, LN02_cos[3], LN01_cos[1],LN02_cos[2])
y2<-c(antipordal_j, LN02_sin[3], LN01_sin[1],LN02_sin[2])
z2<-c(antipordal_k,AP02,AP01,AP02)
quads3d(x2,y2,z2,color=rgb(0,0,1))

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Cube006")

ただしこの「傾いた立方体」扱いが中々難しいのです。というか実質上「ハミルトンの四元数(Hamilton's Quaternion)」の世界。2次元座標系と3次元座標系の往復も含めi^2=j^2=k^2=ijk=-1,ij=k,jk=i,ki=j,ji=-k,kj=-i,ik=-jなる概念との格闘が待ち構えていたりします。
【Rで球面幾何学】ハミルトンの四元数(Hamilton's Quaternion)は何を表しているのか？

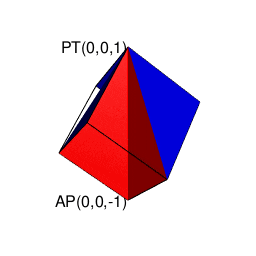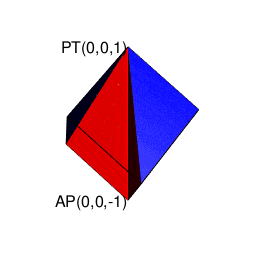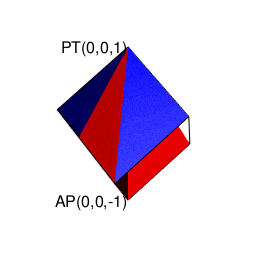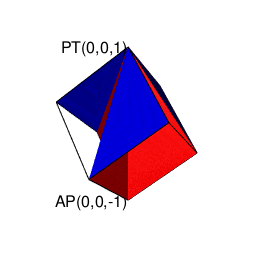
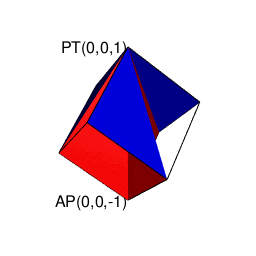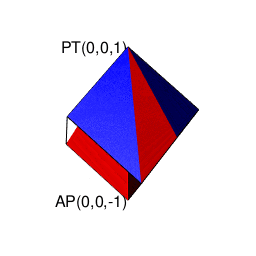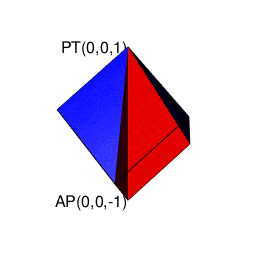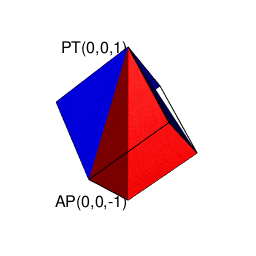
##【2^n3^m集と2^n集の往復】立方体(Cube)と正方形(Square)の往復

そこで正十二面体における「屋根掛け法」でもやってた事ですが、立方対角線=対蹠の対(Set)の位置をズラし、頂点分布を[1,3,3,1]から[0,4,4,0]に変更します(転がして「頂点と頂点の対」から「面と面の対」へ)。

library(rgl)
#頂点座標=8個
texts3d(0,0,0,texts=c("(0,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,0,texts=c("(0,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,0,texts=c("(1,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,0,1,texts=c("(0,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,1,texts=c("(1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,1,texts=c("(0,1,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,1,texts=c("(1,1,1)"),col=rgb(0,0,0),adj=1.0)

#正六面体(Square)本体(6面)の枠線

lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(0,0,0,0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(1,1,1,1,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)

#立方体面描画
x1<-c(0,1,1,0)
y1<-c(0,0,1,1)
z1<-c(0,0,0,0)
quads3d(x1,y1,z1,color=rgb(0,1,0))

x2<-c(0,1,1,0)
y2<-c(0,0,1,1)
z2<-c(1,1,1,1)
quads3d(x2,y2,z2,color=rgb(0,1,0))

x3<-c(0,0,0,0)
y3<-c(0,1,1,0)
z3<-c(0,0,1,1)
quads3d(x3,y3,z3,color=rgb(1,0,0))

x4<-c(1,1,1,1)
y4<-c(0,1,1,0)
z4<-c(0,0,1,1)
quads3d(x4,y4,z4,color=rgb(1,0,0))

x5<-c(0,0,1,1)
y5<-c(0,0,0,0)
z5<-c(0,1,1,0)
quads3d(x5,y5,z5,color=rgb(0,0,1))

x6<-c(0,0,1,1)
y6<-c(1,1,1,1)
z6<-c(0,1,1,0)
quads3d(x6,y6,z6,color=rgb(0,0,1))

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square002") 

この状態は立方眼(Square Grid)や平方眼(Cube Grid)の連続に埋め尽くされる「デカルト座標系の世界(Cartesian Coordinate System Set)」と極めて相性が良く「X軸、Y軸,Z軸それぞれについて四面=四辺の長さを0や1(その正方形や立方体の共通辺長)に設定する事で平面と立体の間を往復出来る」特徴を備えているのです。
【Rで球面幾何学】何故「正方形」ではCos(θ)+Sin(θ)iが成立するのか？

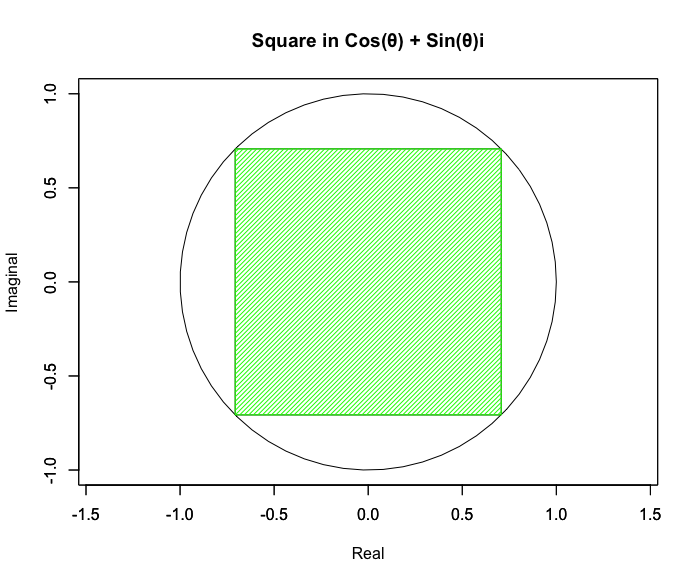
中心からの距離に比例して自己相似型が現れますが、平面充填に際しては平方数、空間充填に際しては立方数がその増分となります。平方対角線sqrt(2)に対応するx^2,立方対角線sqrt(3)に対応するx^3といった具合…
平方数(Square Number) - Wikipedia
立方数(Cubic Number) - Wikipedia

#平方数
>f0<-function(x){return(x^2)}
>c0<-c(0:5)
>f0(c0)
[1]  0  1  4  9 16 25

#立方数
> f0<-function(x){return(x^3)}
> c0<-c(0:5)
> f0(c0)
[1]   0   1   8  27  64 125

##ここまでの全体像の俯瞰

とりあえず、ここまでの遷移図(Transition Diagram)が以下。ちなみに「四角形は(対角線に沿って)三角形に分割可能」「正六面体は正八面体と双対関係」という要素も追加されています。

library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Triangle(s)","Tetrahedrons",
"Tetrahedrons","Triangle(s)",
"Triangle(s)","Hexagon",
"Hexagon","Triangle(s)",
"Triangle(s)","Square",
"Square","Triangle(s)",
"Hexagon","Cube",
"Cube","Hexagon",
"Cube","Octahedron",
"Octahedron","Cube",
"Square","Octahedron",
"Octahedron","Square",
"Cube","Square",
"Square","Cube"
))
plot(gd,layout=layout.fruchterman.reingold)

上記の様に必ずしも全ての変遷が「デカルト座標系の世界(Cartesian Coordinate System Set)」上において納得のいく形で展開する訳ではありませんが…人間はなんとかイメージ的に上手く折り合いを見つけてしまうものなんですね。

##【2^n3^m集から2^n3^m5^l集への遷移】正八面体(Octahedron)から正十二面体(Dodecahedron)への不可逆的変換

さらにこんな情報を仕入れました。
正八面体を上から見た図と東大の問題

• 正八面体を上から見た図…正八面体の頂点分布[1,4,1]は、転がすと[0,3,3,0]に変換される。
  
• 正八面体を底面に平行な平面で切断した図
  
  
  この断面は正十二面体の断面図を連想させる。
  【オイラーの多面体定理と正多面体】正12面体(Regular Dodecahedron)の作図について。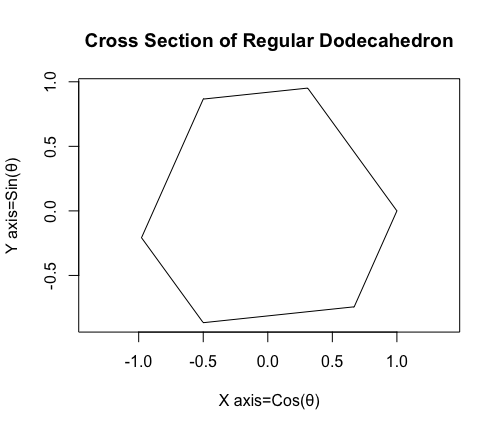
  

要するに以下の操作により正八面体から頂点分布[1,3,6,6,3,1]の正十二面体への変換が可能になるという事です。

• 正八面体を転がして、その頂点分布を[1,4,1]から[0,3,3,0]へと変換する。
• それぞれの対蹠から３辺を伸ばす。
• 3頂点の中間断面二個から、それぞれ断面図に沿った新たな6頂点の断面二個を生成する。

考え方としては「それぞれの対蹠から三辺ずつ伸ばし、さらにそこから二辺ずつ伸ばす二段階変遷」に近いものがありますね。
【オイラーの多面体定理と正多面体】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)

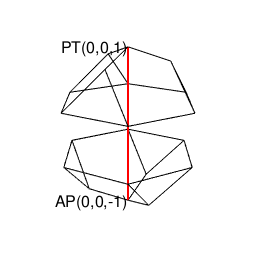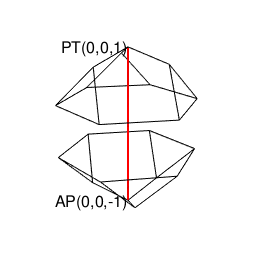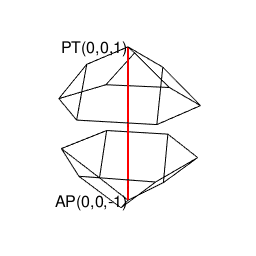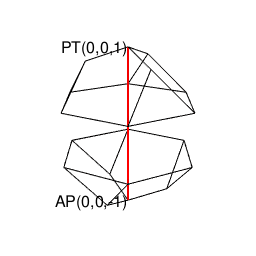
ちゃんとした図示はそのうちに。とりあえず、以下続報…