強化学習の評価でよく使われるAtariのゲームですが、ついに57全てのゲームで人間を超えた手法が現れたようです。
早速実装してみました。
※ネット上の情報をかき集めて自分なりに実装しているので正確ではない点はご了承ください
※解釈違いの内容がある可能性もご注意ください(理解が追いついていない部分があります)
コード全体
本記事で作成したコードは以下です。
- github
-
GoogleColaboratory(実行結果付き)
※GoogleColaboratoryはmultiprocessingの相性が悪いらしく1Actorのみの学習となります)
※MountainCarの学習をのせています
追記:自作フレームワークを作成しています。そちらの実装の方が正確なコードとなります。
目次
構成としては前半が技術解説で後半が実装の説明になります。
- Agent57とは
- NGU(Never Give Up)の解説
- 内部報酬について
- POMDPへの対策(UVFAとRetrace)
- Agent57の解説
- 行動価値関数(Q関数)について
- メタコントローラーについて
- 実装
- 内部報酬の実装
- 探索ポリシーの実装
- 行動価値関数(Q関数)モデルの実装
はじめに
Agent57はいわゆるDQN系列の強化学習手法となります。
DQN系列のAgent57までの技術に関しては以前記事にしているのでよかったらどうぞ
- 【強化学習】OpenAI Gym×Keras-rlで強化学習アルゴリズムを実装していくぞ(準備編)
- 【強化学習】OpenAI Gym×Keras-rlで強化学習アルゴリズムを実装していくぞ(Q学習編)
- 【強化学習】OpenAI Gym×Keras-rlで強化学習アルゴリズムを実装していくぞ(DQN編)
- 【強化学習】Keras-rlでRainbowを実装/解説
- 【強化学習】Keras-rlでApe-Xを実装/解説(並列プログラミング)
- 【強化学習】2018年度最強と噂のR2D2を実装/解説してみた
- 【強化学習】R2D2を実装/解説してみたリベンジ 解説編(Keras-RL)
- 【強化学習】R2D3を実装/解説してみた(Keras-RL)
追記: Agent57の記事をもう一つ書きました
・Q学習にAgent57までの技術を実装してみた
Agent57について
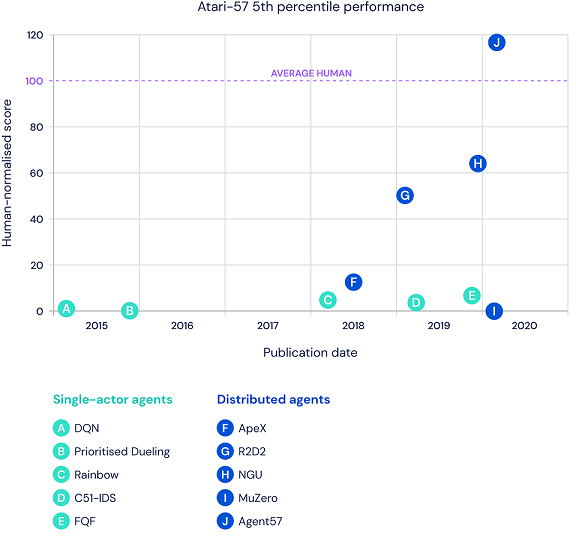
強化学習の指標として Atari2600 の57個のゲームがよく使われていますが、ついに57個全てのゲームで人間の性能を超えた強化学習手法が現れました。
既存の手法では Montezuma's Revenge 等、学習が難しいゲームがありましたが Agent57 ではちゃんと学習できるようになったみたいです。
以下はDeepMindの記事より引用した各手法の比較です。
F(ApeX)やG(R2D2)もすごいと思いましたが、それを超えて圧倒的な性能ですね。
・参考
Agent57: Outperforming the human Atari benchmark
Atari完全制覇! Atari57ゲーム全てで人間を超えたAgent57とは!?
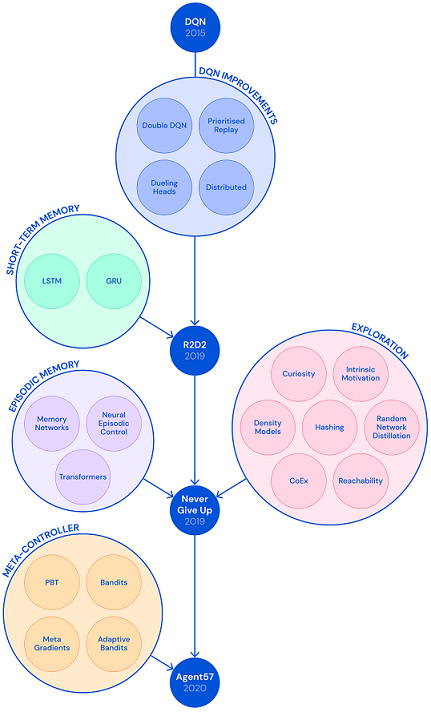
Agent57に至るまで
(図はDeepMindの記事より引用)
本記事では NGU(Never Give Up) と Agent57 について解説します。
図の通りAgent57は既存のDQN手法を改良して実現しています。
過去の手法について気になった内容は私の過去の記事を参考にしてもらえればと思います。
NGU/Agent57で大きく変わった部分は、探索(Exploration)と搾取(Exploitation)に焦点を当て、報酬が得られにくい環境に対しても効率的に探索できる仕組みを導入している点です。
それ以外にもいろいろな手法が取り入れられているので1つずつ説明していきたいと思います。
NGU(Never Give Up)
強化学習において未知の領域を探索(exploration)する事と報酬を手に入れる事(搾取:exploitation)はトレードオフの関係にあります。
既存の手法では報酬が疎な(報酬を手に入れるまでが長い)ゲームではうまく学習できない問題がありました。
そこでNGUでは報酬に内部報酬(Intrinsic Reward)を追加することで効率的な探索を実現しています。
内部報酬は以下の3つの条件を満たすように設定されます。
- 1エピソード内で同じ状態を訪れないようにする(強め)
- トレーニング全体で同じ状態を訪れないようにする(弱め)
- エージェントの行動に関係なく変化する状態を無視する
・参考
(論文)Never Give Up: Learning Directed Exploration Strategies
Never give Up! Atari完全制覇に繋がる、困難な環境でも諦めずに探索を行う強化学習!
内部報酬(Intrinsic Reward)
NGUでは外部報酬(Extrinsic Reward:従来の報酬)に対して内部報酬(Intrinsic Reward)を加える形で報酬を定義します。
$$r_{t}=r^e_t + \beta r^i_t$$
ここで $r^e_t$ が外部報酬、$r^i_t$ が内部報酬で、$\beta$ は内部報酬を重みづけする定数です。
そしてこれらを足し合わせた $r_{t}$(拡張報酬)を用いてトレーニングを行います。
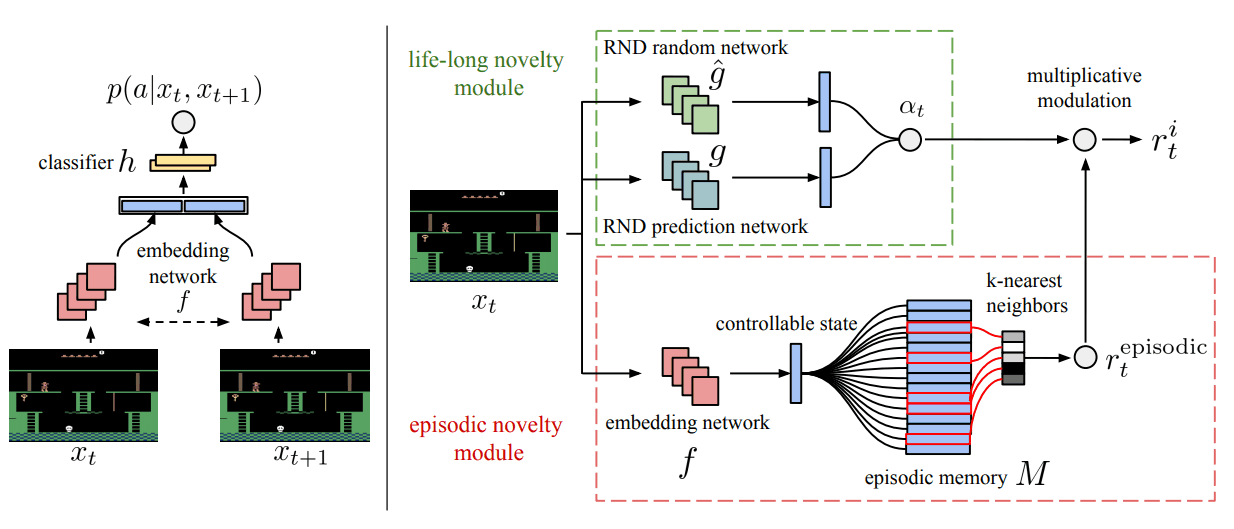
では内部報酬を見ていきます。(図は論文より引用、以降この図を図Aといいます)
内部報酬は生涯記憶部(life long novelty module:図Aの右側の緑枠)とエピソード記憶部(episodic novelty module:図Aの右側の赤枠)から作成されます。
生涯記憶部からは $\alpha_t$、エピソード記憶部からは $r^{episode}_t$ という値を生成し、以下のように合成します。
$$ r^i_t = r^{episode}_t・min ( max ( \alpha _{t}, 1 ), L ) $$
日本語で書くと、内部報酬 = エピソード記憶部 × 生涯記憶部 です。
※ただし、生涯記憶部は1以下なら1、L以上ならLになる
※ L は最大スケール報酬を表す定数です(論文ではL=5)
まずはエピソード記憶部から見ていきます。
エピソード記憶部(episodic novelty module)
エピソード記憶部では1エピソード内で同じ状態を訪れないように報酬を決めます。
全体のフローは以下です。(図Aの赤枠部分に該当)
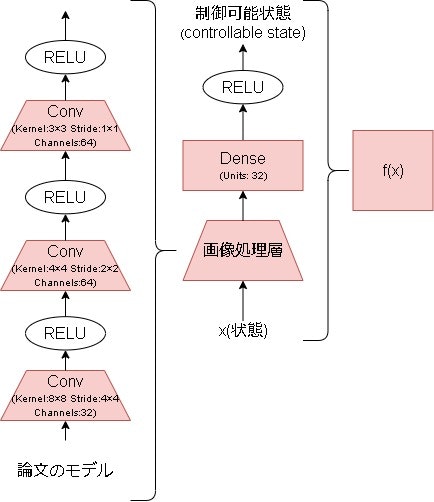
- 埋め込み関数(embedding network)を用いて現在の状態から制御可能状態(controllable state)を出す
- 制御可能状態とエピソードメモリ(episodic memory M)より、k近傍法(k-nearest neighbors)で現在の状態の訪問回数の近似値を出す
- 訪問回数の近似値より、エピソード記憶部($r^{episode}_t$) を出す
- 制御可能状態をエピソードメモリに追加する
埋め込み関数と訪問回数の近似値に関しては後述します。
エピソードメモリは1エピソードの最初に初期化されます。
これにより1エピソード内での訪問回数を判断しているようです。
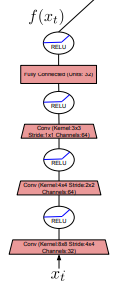
埋め込み関数(embedding network)
埋め込み関数は制御可能状態を生成するニューラルネットワークの関数です。
現在の状態をp次元に圧縮するだけのシンプルなニューラルネットワークのようですね。
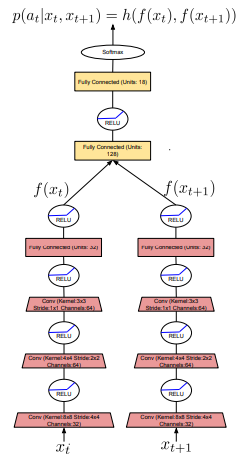
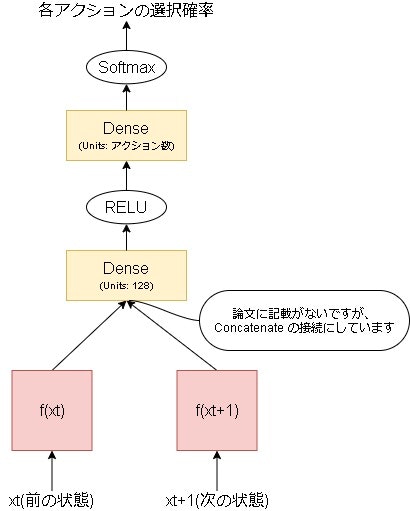
問題は学習で、以下のように Siamese network に見立てて学習します。
(この図は図A左側の詳細な図になります)
入力は1つ前の状態と現在の状態で、出力が各アクションの選ばれる確率です。
要するに、前の状態と今の状態の差分からどのアクションが実行されたかを学習するネットワークとなります。
このネットワークで行動に紐づいて変化する状態のみを学習していると思われます。
参考:【深層距離学習】Siamese NetworkとContrastive Lossを徹底解説
k近傍法による訪問回数の近似
エピソード記憶部($r^{episode}_t$)は訪問回数をもとに算出します。
訪問回数はエピソードメモリと現在の状態より、k近傍法を用いて近似することで算出しています。
以下数式による説明です。
エピソード記憶部($r^{episode}_t$)は以下です。
$$ r^{episode}_t = \frac{1}{ \sqrt{ n(f(x _{t})) } }$$
$n(f(x_t))$ が訪問回数です。
訪問回数はカーネル関数Kを用いて近似するとの事で、以下になります。
$$ \frac{1}{ \sqrt{ n(f(x_t)) } } \approx \frac{1}{ \sqrt{ \sum_(f_i \in N_k)K(f(x_t), f_i) } + c} $$
cは最小の疑似訪問回数を保証する定数です。(c=0.001)
Kは、メモリ内の制御可能状態と今の制御可能状態とのk近傍法により計算されます。
$$ K(x,y) = \frac{\epsilon}{ \frac{d^2(x,y)}{d^2_m} + \epsilon} $$
$\epsilon$ は小さな定数です。($\epsilon$=0.001)
d はユークリッド距離を表し、$d^2_m$はユークリッド距離の移動平均を表します。
生涯記憶部(life long novelty module)
生涯記憶部はRND(Random Network Distillation)が用いられています。
・参考
Exploration by Random Network Distillation の効果を MountainCar で試した。
(論文) Exploration by Random Network Distillation
RNDの説明ですが、普通はある状態において未知の状態かどうかを判断したい場合、訪問回数を数えて訪問回数が多いほど既知の状態と考えるものです。
しかしRNDでは逆転の発想をしています。
参考ブログの方の例えがうまかったので使わせてもらいますが、RNDではまずスクラッチの地図を用意します。
最初は地図は銀紙で覆われていますが、訪れるごとに少しずつ削れて行きます。
この削れ具合を見て、どれだけ未知かを判断する方法がRNDとなります。
ではこれをどう実現するかというと、同じ構造の2つのニューラルネットワークを用意します。(A,Bとします)
Aは初期状態のままにし、BはAに近づくように学習します。
このBの学習が銀紙を削る行為に相当します。
これにより、AとBを比べて誤差が大きい=探索されていない場所、誤差が小さい=よく探索された場所になるわけですね。
MDPとPOMDP
強化学習の前提の話に戻ります。
Q学習ではMDP(マルコフ決定過程)の確率モデルが前提となっています。
このモデルを簡単に言うと、ある状態でアクションを実行するとランダムな状態に移行し決まった報酬がもらえるというモデルです。
(一般的な強化学習のモデルですね)
しかし、NGUでは内部報酬が加えられるので同じ状態に移行しても報酬が変わります。
ですのでNGUはMDPではなく、POMDP(部分観測マルコフ決定過程)のモデルとして考える必要があります。
・参考
マルコフ決定過程(Wikipedia)
部分観測マルコフ決定過程(Wikipedia)
しかし、POMDPとして考えることはMDPに比べてはるかに難しくなるのでNGUでは次の2つの回避策を導入しています。
- 外部報酬をQネットワークに直接入力する
- エピソード内のすべての入力(状態、アクション、および報酬)の履歴を要約する内部状態表現を維持
また、内部報酬による探索行動は報酬に直接加るので、探索行動を簡単にオフにする事が出来ません。
この問題を解決するために、NGUでは外部報酬と探索行動を同時に学習する手法を提案しています。
UVFA(Universal Value Function Approximators)
DQNはある状態を入力としてQ値を推定するのが一般的です。
ここで、入力を状態だけではなく目標(goal)も加え一般化した価値関数がUVFAです。
NGUはこのUVFAを用いますが、目標の代わりに$\beta$(内部報酬の反映率:探索率)を入力としています。
これにより探索行動も同時に学習することを提案しています。
$\beta = 0$ の場合は探索がオフの場合の結果を取得でき、$\beta > 0$は探索がオンの場合の結果を取得できるようになるわけですね。
・参考
(DeepMind社のスライド) Universal Value Function Approximators
(論文) Universal Value Function Approximators
Retrace
追記:Retraceについては再度勉強し、新たに記事を書いています。
やっと理解できたと思うRetraceについて丁寧に解説【強化学習】
以下は古い内容となります。
Q学習はTD学習の中でも Off-Policy という探索方法をとっています。
(逆にTD学習で On-Policy な探索の一つに Sarsa というのがあります)
違いは更新するQ値の参照先で、Off-Policyの場合は方策に従いません。
(Q学習ではQ値が最大となるアクションを選んでいます)
On-Policy の場合は方策に従い取得します。
(例えば ε-greedy で探索している場合は、参照先も ε-greedy を使います)
Off-Policy で問題となるのが実際に行動した方策(Behavior policy)と学習したい方策(Target policy)が異なる点です。
これが異なるといつまでたっても値が収束しない(安全でない)可能性があります。
Retraceの論文ではこれを解決するために4つの手法(既存手法3つ+Retrace)を比較し、Retrace が優れている事を示しています。
Retrace を簡単に言うと過去の結果を元に方策を予測し、その差分で学習をコントロールする方法です。
(学習のコントロールに使う係数を cutting traces coefficients($c_s$) と言っています)
NGUでは Retrace を取り入れています。
・参考
今さら聞けない強化学習(10): SarsaとQ学習の違い
強化学習のOn-PolicyとOff-Policy
(Off-policyに関する論文1) Q(λ) with Off-Policy Corrections
(Off-policyに関する論文2) Off-Policy Temporal-Difference Learning with Function Approximation
(DeepMind社のスライド)off-policy deep RL
(Retraceの論文) Safe and efficient off-policy reinforcement learning
(Retrace論文の日本語スライド)safe and efficient off policy reinforcement learning
強化学習理論の基礎2
[Review] UCL_RL Lecture05 Model Free Control
割引率
割引率($\gamma$)は$\beta$(内部報酬の反映率)に依存し変化させます。
$\beta=0$ の場合は $\gamma=max$、$\beta=max$ の場合は $\gamma=min$ とします。
(具体的には $\beta=0$ は $\gamma=0.997$、$\beta=max$ は $\gamma=0.99$)
探索時は外部報酬の影響が小さくなるのでその調整のための割引率ですね。
Agent57
NGUで効率的な探索を実現できましたが、一部のゲームでは単純なランダム探索と同等のスコアしか出ない場合もありました。
また、NGUの欠点の1つに学習の進捗に関係なく探索してしまう点がありました。
Agent57では以下を提案し、これらを改善しました。
- 外部報酬と内部報酬を分離する新しいパラメータを導入し、内部報酬の学習を安定させた
- メタコントローラーを導入し、探索率を優先順位に従って選択できるメカニズムを導入した
(論文) Agent57: Outperforming the Atari Human Benchmark
行動価値関数(Q関数)のアーキテクチャの変更
NGUでは学習が不安定になる場合がありました。
外部報酬と内部報酬のスケール・スパース性が異なる場合や、ある報酬のみが他の報酬に比べて過剰に反応する場合に起こります。
Agent57では、外部報酬と内部報酬で報酬の性質が非常に異なる場合に行動価値関数を学習することは難しいと推測し、行動価値関数のアーキテクチャの変更を提案しました。
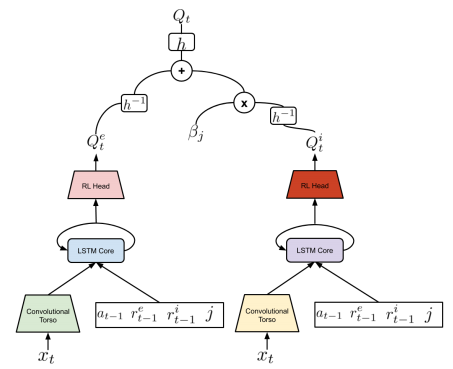
具体的には外部報酬を学習する $Q(x,a,j;\theta^e)$ と内部報酬を学習する $Q(x,a,j;\theta^i)$ に行動価値関数を分割し、以下の数式でQ値を求めます。
(ベルマン演算子(transformed Bellman operator)に基づいてるそうです)
$$ Q(x,a,j;\theta) = h(h^{-1}(Q(x,a,j;\theta^e)) + \beta_j h^{-1}( Q(x,a,j;\theta^i)))$$
$\beta_j$は内部価値関数の反映率(探索率)、hはベルマン演算子関数?です。
hはあまりよく分かっていませんが、R2D2のrescaling関数と同じもので、以下となります。
$$ h(z) = sign(z)(\sqrt{|z|+1}-1 ) + \epsilon z $$
$$ h^{-1}(z) = sign(z)(( \frac{ \sqrt{1+4\epsilon (|z|+1+\epsilon} + 4\epsilon }{ 2\epsilon } ) -1)$$
メタコントローラー
NGUとAgent57では内部報酬を用いて探索率($\beta_j$)を設定できるようになりました。
ただNGUでは、探索率は各Actor毎に固定としていました。
例えばActorが4の場合は以下みたいな感じです。(値は仮です)
Actor1:$\beta_j$=0(探索なし)
Actor2:$\beta_j$=0.1(なんとなく探索)
Actor3:$\beta_j$=0.2(少し探索)
Actor4:$\beta_j$=0.3(そこそこ探索)
探索率はトレーニングの早い段階では高めの値を用いた方がいいですが、トレーニングが進むと低い値を用いた方がいい事が予想されます。
そこで効率のいい探索率を選択する手法を取り入れるためにAgent57ではメタコントローラーを提案しました。
メタコントローラーでは、効率のいい探索率の選択を、どの探索ポリシー(NGUでいうActor)を選べば最大の報酬を得られるかという多腕バンディット問題(Multi-armed bandit problem:MAB問題)に見立ててこれを解決しています。
(ここでの報酬は、1エピソード内における割引されていない外部報酬の合計を指します)
・参考
私が以前書いた記事:【強化学習】複数の探索ポリシーを実装/解説して比較してみた(多腕バンディット問題)
多腕バンディット問題の理論とアルゴリズム
強化学習入門:多腕バンディット問題
多腕バンディット問題(Multi-armed bandit problem:MAB問題)
MAB問題を簡単に言うと、複数のスロット(アーム)から一定回数選んだ場合に報酬を最大にする問題です。
例えばスロットが4つ(A,B,C,D)あったとします。
100回スロットを選んだあとに賞金が最大になる選び方はどういう選び方でしょうか?という問題です。
4つのスロットが賞金を出す確率は分かりません。
一般的なMAB問題では賞金が出る確率はスロット毎に一定です。(最初に決めた後は変化しない)
しかし Agent57 では報酬の出る確率(報酬結果)が変化していきます。
そのためメタコントローラーでは少し工夫をしています。
sliding-window UCB法
Agent57ではMAB問題に対するアルゴリズムとしてUCB法を用いています。
しかし報酬が変化するのでそのままではUCB法を適用できません。
そこで、直近の数エピソードのみを対象にUCB法を用いることを提案しています。
これを sliding-window UCB法と論文内では言っています。
直近の数エピソードだけを見る点以外はUCB法と変わりません。
実装
内部報酬(Intrinsic Reward)
埋め込み関数(embedding network)
学習時のネットワーク構造と使用時のネットワーク構造が違う特殊なニューラルネットワークを作る必要があります。
まずは値取得用の埋め込み関数です。
論文には画像処理層といった記載はなく、この記事内での用語となります。(論文は画像入力が前提のため)
次に学習用の埋め込み関数です。
上記の図を実装したコードは以下となります。
※画像入力の場合のモデルとなります
※重みを共有するために各レイヤーには名前を付けています
input_sequence = 入力フレーム数
input_shape = 入力形式
nb_actions = アクション数
c = input_ = Input(shape=(input_sequence,) + input_shape)
c = Conv2D(32, (8, 8), strides=(4, 4), padding="same", name="l0")(c)
c = Conv2D(64, (4, 4), strides=(2, 2), padding="same", name="l1")(c)
c = Conv2D(64, (3, 3), strides=(1, 1), padding="same", name="l2")(c)
c = Dense(32, activation="relu", name="l3")(c)
emb_model = Model(input_, c)
# 入力を2つ作ります
c1 = input1 = Input(shape=(input_sequence,) + input_shape)
c2 = input2 = Input(shape=(input_sequence,) + input_shape)
# 重みを共有しつつ、ネットワークを作ります
l = Conv2D(32, (8, 8), strides=(4, 4), padding="same", name="l0")
c1 = l(c1)
c2 = l(c2)
l = Conv2D(32, (4, 4), strides=(2, 2), padding="same", name="l1")
c1 = l(c1)
c2 = l(c2)
l = Conv2D(64, (3, 3), strides=(1, 1), padding="same", name="l2")
c1 = l(c1)
c2 = l(c2)
l = Dense(32, activation="relu", name="l3")
c1 = l(c1)
c2 = l(c2)
# 結合
c = Concatenate()([c1, c2])
c = Dense(128, activation="relu")(c)
c = Dense(nb_actions, activation="softmax")(c)
emb_train_model = Model([input1, input2], c)
# optimizerは論文より
emb_train_model .compile(
loss='mean_squared_error',
optimizer=Adam(lr=0.0005, epsilon=0.0001))
損失関数ですが、最尤推定法で学習するとしか論文には記載がありませんでした。(多分…)
なのでとりあえず平均二乗誤差にしています。
・参考
闇のKerasのTPU術:入力が2つあるモデルと、入力が1つのモデルの係数を相互転移させる方法
多入力多出力モデル(Keras公式)
次に emb_train_model から emb_model に重みをコピーするコードです。
def sync_embedding_model():
for i in range(4): # layer数分回す
train_layer = emb_train_model.get_layer("l" + str(i))
val_layer = emb_model.get_layer("l" + str(i))
# 重みをコピー
val_layer.set_weights(train_layer.get_weights())
入力がバラバラでさらに重みも共有するすごいモデルができました。。。
埋め込み関数(embedding network)の学習
論文にほとんど書かれていないような…
一応 Embeddings target の更新間隔が1エピソードに1回と書かれています。
Embeddings targetって何ですかね…。
とりあえず学習方法は行動価値関数の学習と同じサンプルを使用して実行し、emb_train_model → emb_model への同期は1エピソードに1回としました。
batch_size = バッチサイズ
def forward(observation):
# 毎フレームの学習のタイミング
# 経験メモリからバッチ用の経験をランダムに取得する
batchs = memory.sample(batch_size)
# データを整形する
state0_batch = [] # 前の状態
state1_batch = [] # 次の状態
emb_act_batch = []
for batch in batchs:
state0_batch.append(batchs["前の状態"])
state1_batch.append(batchs["次の状態"])
# アクションは one-hot vector にしてデータを作成
a = np_utils.to_categorical(
batchs["アクション"],
num_classes=nb_actions
)
emb_act_batch.append(a)
# トレーニング
emb_train_model.train_on_batch(
[state0_batch, state1_batch], # 入力は前の状態と次の状態の2つ
emb_act_batch # 教師はアクション
)
def backward(self, reward, terminal):
if terminal:
# エピソード終了タイミングで同期
sync_embedding_model()
※numpy化は省略
埋め込み関数(embedding network)の値取得
emb_model から値を取り出すだけですね。
state = 現在の状態
cont_state = emb_model.predict([state], batch_size=1)[0]
※numpy化は省略
エピソード記憶部の計算
ここの計算ですが幸いなことに論文内に疑似コードが書いてありました。
それをpython風疑似コードで表すと以下です。
def calc_int_episode_reward(():
state = 現在の状態
k = k近傍法での数(k=10)
epsilon = 0.001
c = 0.001
cluster_distance = 0.008
maximum_similarity = 8
# 埋め込み関数から制御可能状態を取得
cont_state = embedding_network.predict(state, batch_size=1)[0]
# エピソードメモリ内の全要素とユークリッド距離を求める
euclidean_list = []
for mem_cont_state in int_episodic_memory:
euclidean = np.linalg.norm(mem_cont_state - cont_state)
euclidean_list.append(euclidean)
# 上位k個が対象
euclidean_list.sort()
euclidean_list = euclidean_list[:k]
# ユークリッド距離2乗
euclidean_list = np.asarray(euclidean_list) ** 2
# 平均を出す
ave = np.average(euclidean_list)
# 訪問回数を近似する(数式のΣの計算)
count = 0
for euclidean in euclidean_list:
d = euclidean / ave
# 論文で説明がないけど疑似コードに書いてある…
# ある一定の距離は最短距離にまとめてる?
d -= cluster_distance
if d < euclidean_list[0]:
d = euclidean_list[0]
count += epsilon / (d+epsilon)
s = np.sqrt(count) + c
# ここも論文に説明はないけど、ある程度小さい値は0にまるめてる?
if s > maximum_similarity:
episode_reward = 0
else:
episode_reward = 1/s
# 論文の疑似コードにはないが、エピソードメモリに制御可能状態を追加
int_episodic_memory.append(cont_state)
if len(int_episodic_memory) >= 30000:
int_episodic_memory.pop(0)
return episode_reward
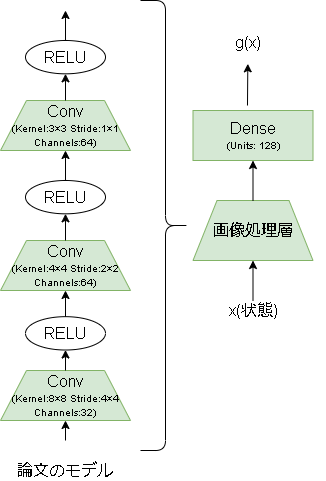
生涯記憶部(life long novelty module)
RNDモデル
RNDのモデルは以下です。
出力に大きな意味はありません。
画像処理層ありの場合のコードは以下です。
def build_rnd_model():
# 入力層
c = input = Input(shape=(input_sequence,) + input_shape)
# 画像処理層
c = Conv2D(32, (8, 8), strides=(4, 4), padding="same")(c)
c = Conv2D(64, (4, 4), strides=(2, 2), padding="same")(c)
c = Conv2D(64, (3, 3), strides=(1, 1), padding="same")(c)
# Dense
c = Dense(128)(c)
model = Model(input, c)
# loss、optimizerは論文より
model.compile(
loss='mean_squared_error',
optimizer=Adam(lr=0.0005, epsilon=0.0001))
return model
# train_model が target_model に近づくイメージです
rnd_target_model = build_rnd_model()
rnd_train_model = build_rnd_model()
RNDの学習
こちらも論文にほとんど書かれていないと思います…
埋め込み関数と同様に行動価値関数の学習と同じサンプルを使用しています。
(学習に使用した=訪問した、という解釈で学習させています(けどちょっとあやしいかも…))
def forward(observation):
# 毎フレームの学習のタイミング
# 経験メモリからバッチ用の経験をランダムに取得する
batchs = memory.sample(batch_size)
# データを整形する
state0_batch = [] # 前の状態
state1_batch = [] # 次の状態
for batch in batchs:
state0_batch.append(batchs["前の状態"])
state1_batch.append(batchs["次の状態"])
# target の値を取得
rnd_target_val = rnd_target_model.predict(state1_batch, batch_size)
# トレーニング
rnd_train_model.train_on_batch(state1_batch, rnd_target_val)
※numpy化は省略
生涯記憶部の計算
生涯記憶部の計算式ですが、まず rnd_target_model と rnd_train_model の2乗誤差を出します。
$$ err(x_t) = || \hat{g}(x_t;\theta) - g(x_t)||^2$$
それを元に以下の計算式で生涯記憶部を出します。
$$ \alpha_t = 1 + \frac{ err(x_t) - \mu_e }{ \sigma_e }$$
ここで $\sigma_e$ は $err(x_t)$ の標準偏差、$\mu_e$ は $err(x_t)$ の平均になります。
標準偏差と平均が出てきましたね…
どうやって計算するかは論文に記載がありませんが…、計算するには過去の結果を保存しないといけないですね。
とりあえず $err(x_t)$ を保存する配列を作りました。
ただ、無限に追加されると困るので上限も作っています。
以下コードです。
#--- 計算用の変数
rnd_err_vals = []
rnd_err_capacity = 10_000
#--- 計算部分
def calc_int_lifelong_reward():
state = 現在の状態
# RNDの取得
rnd_target_val = rnd_target_model.predict(state, batch_size=1)[0]
rnd_train_val = rnd_train_model.predict(state, batch_size=1)[0]
# 2乗誤差を出す
mse = np.square(rnd_target_val - rnd_train_val).mean()
rnd_err_vals.append(mse)
if len(rnd_err_vals) > rnd_err_capacity:
rnd_err_vals.pop(0)
# 標準偏差
sd = np.std(rnd_err_vals)
if sd == 0:
return 1
# 平均
ave = np.average(rnd_err_vals)
# life long reward
lifelong_reward = 1 + (mse - ave)/sd
return lifelong_reward
内部報酬の計算
内部報酬は以下の数式です。
$$ r^i_t = r^{episode}_t・min ( max ( \alpha _{t}, 1 ), L ) $$
L = 5
episode_reward = エピソード記憶部
lifelong_reward = 生涯記憶部
if lifelong_reward < 1:
lifelong_reward = 1
if lifelong_reward > L:
lifelong_reward = L
intrinsic_reward = episode_reward * lifelong_reward
探索率(β)と割引率(γ)
探索ポリシーは探索率(β)と割引率($\gamma$)のペアで表され、以下の式で計算されます。
割引率はNGUとAgent57で計算式が違います。(一応両方かいておきます)
まずは探索率の計算式です。
\beta_i = \left\{
\begin{array}{ll}
0 \qquad (i = 0) \\
\beta \qquad (i = N-1) \\
\beta・\sigma(10\frac{2i-(N-2)}{N-2}) \quad (otherwise)
\end{array}
\right.
$\sigma$ はシグモイド関数で、$\beta$ は反映率の最大値です。
def sigmoid(x, a=1):
return 1 / (1 + np.exp(-a * x))
def create_beta_list(N, max_beta=0.3):
beta_list = []
for i in range(N):
if i == 0:
b = 0
elif i == N-1:
b = max_beta
else:
b = 10 * (2*i-(N-2)) / (N-2)
b = max_beta * sigmoid(b)
beta_list.append(b)
return beta_list
NGUの割引率です。
$$ \gamma_i = 1 - exp \Bigl( \frac{ (N-1-i)log(1-\gamma_max) + (ilog(1-\gamma_min)) }{N-1} \Bigr)$$
def create_gamma_list_ngu(N, gamma_min=0.99, gamma_max=0.997):
if N == 1:
return [gamma_min]
if N == 2:
return [gamma_min, gamma_max]
gamma_list = []
for i in range(N):
g = (N - 1 - i)*np.log(1 - gamma_max) + i*np.log(1 - gamma_min)
g /= N - 1
g = 1 - np.exp(g)
gamma_list.append(g)
return gamma_list
Agent57の割引率です。
\gamma_j = \left\{
\begin{array}{ll}
\gamma0 \qquad (j=0) \\
\gamma1 + (\gamma0 - \gamma1)\sigma(10 \frac{2i-6}{6} ) \qquad (j \in (1,...,6)) \\
\gamma1 \qquad (j=7) \\
1-exp(\frac{(N-9)log(1-\gamma1) + (j-8)log(1-\gamma2)}{N-9}) \quad (otherwise)
\end{array}
\right.
def create_gamma_list_agent57(N, gamma0=0.9999, gamma1=0.997, gamma2=0.99):
gamma_list = []
for i in range(N):
if i == 1:
g = gamma0
elif 2 <= i and i <= 6:
g = 10*((2*i-6)/6)
g = gamma1 + (gamma0 - gamma1)*sigmoid(g)
elif i == 7:
g = gamma1
else:
g = (N-9)*np.log(1-gamma1) + (i-8)*np.log(1-gamma2)
g /= N-9
g = 1-np.exp(g)
gamma_list.append(g)
return gamma_list
内部報酬のモデル(UVFA)
ここは理解が怪しいです…。
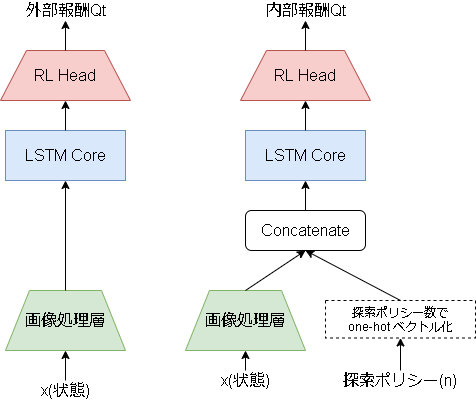
以下の図はAgent57の行動価値関数のモデルです。
右下に [アクション, 外部報酬, 内部報酬, 探索率] の記載があります。
しかし、これをどう追加するかが書かれていないんですよね…
とりあえず以下のように内部報酬の行動価値関数のみに探索率をohe-hotベクトルで追加しています。
(内部報酬や外部報酬をそのまま入力すると学習しなくなったりしたんですよね…)
以下コードです。
内部報酬用の行動価値関数のみの記載です。
((UVFA)とコメントがある部分がUVFAで変更している部分です)
from keras.utils import to_categorical
# Q関数用のモデルを作成する箇所
def build_actval_int_model():
# 入力層
c1 = input1 = Input(shape=(input_sequence,) + input_shape)
c2 = input1 = Input(shape=(policy_num,)) # (UVFA)追加
# 画像処理層
c1 = Conv2D(32, (8, 8), strides=(4, 4), padding="same")(c1)
c1 = Conv2D(64, (4, 4), strides=(2, 2), padding="same")(c1)
c1 = Conv2D(64, (3, 3), strides=(1, 1), padding="same")(c1)
c = Concatenate()([c1, c2]) # (UVFA)追加
# lstm
c = LSTM(512)(c)
# dueling network
c = DuelingNetworkのモデルを作成(c)
model = Model([input1, input2], c) # (UVFA)変更
model.compile(loss=clipped_error_loss, optimizer=Adam(lr=0.0001, epsilon=0.0001))
return model
# モデルを作成
actval_int_model = build_actval_int_model()
actval_int_model_target = build_actval_int_model()
内部報酬モデルのトレーニング
# 毎フレーム
def forward(observation):
# batchデータを取得
batchs = memory.sample()
# データを整形
state0_batch = []
state1_batch = []
policy_batch = []
for batch in batchs:
state0_batch.append(batchs["前の状態"])
state1_batch.append(batchs["次の状態"])
# 探索ポリシーを one-hot化
t = to_categorical(batchs["探索ポリシー"], num_classes=policy_num)
policy_batch.append(t)
# 入力は stateと探索ポリシー
state0_batch = [state0_batch, policy_batch]
state1_batch = [state1_batch, policy_batch]
# Q値を出す例
state0_qvals = actval_int_model.predict(state0_batch, batch_size)
(更新用の state0_qvals の計算)
# 学習
actval_int_model.train_on_batch(state0_batch, state0_qvals)
Q値の計算
NGUでのQ値の計算は、Agent57の行動価値関数の分割によりなくなったので省略します。
Agent57でのQ値の計算式は、内部報酬と外部報酬の組み合わせた以下になります。
$$ Q(x,a,j;\theta) = h(h^{-1}(Q(x,a,j;\theta^e)) + \beta_j h^{-1}( Q(x,a,j;\theta^i)))$$
def rescaling(x, epsilon=0.001):
if x == 0:
return 0
n = math.sqrt(abs(x)+1) - 1
return np.sign(x)*n + epsilon*x
def rescaling_inverse(x, epsilon=0.001):
if x == 0:
return 0
n = math.sqrt(1 + 4*epsilon*(abs(x)+1+epsilon)) - 1
return np.sign(x)*( n/(2*epsilon) - 1)
def get_qvals():
state = 現在の状態
policy_index = 探索ポリシー
# 外部のQ値を出す
qvals_ext = avtval_ext_model.predict(state, batch_size=1)[0]
# 探索ポリシーone-hot
policy_onehot = to_categorical(policy_index, num_classes=policy_num)
# 内部のQ値を出す
qvals_int = avtval_int_model.predict([state, policy_onehot], batch_size=1)[0]
# 探索率
beta = int_beta_list[policy_index]
# Q値を計算
qvals = []
for i in range(nb_actions):
q_ext = rescaling_inverse(qvals_ext[i])
q_int = rescaling_inverse(qvals_int[i])
qval = rescaling(q_ext + beta * q_int)
qvals.append(qvals)
return qvals
UVFAについて追記(2020/8/29)
[アクション, 外部報酬, 内部報酬, 探索率]の追加ですが、外部報酬を含め全部実装しても学習できました。
github はコードを更新しています。
実装ではアクションと探索率はone-hotベクトル化して、
[アクション(one-hot), 外部報酬, 内部報酬, 探索率(one-hot)]みたいな感じで1次元の配列に全て並べて入力としています。
Retrace
追記:上でも書いていますが、Retraceについては再度勉強し、新たに記事を書いています。
やっと理解できたと思うRetraceについて丁寧に解説【強化学習】
以下は古い内容となります。
先に言いますが、Retraceの実装は保留にしています(内容理解できず…)
理解できていない内容を記載しておきます。
Retrace関数は以下です。
$$ c_s = \lambda min(1, \frac{\pi(A_s|X_s)}{\mu(A_s|X_s)}) $$
$\pi$ が探索ポリシー(Target Policy)で、$\mu$が振る舞いポリシー(Behavior Policy)の各アクションの確率分布になります。
ただ、DQNで探索ポリシーは完全greedy(Q値最大値のみを選ぶ)なので、確率分布はQ値最大値のアクションが1、それ以外が0になる気がします。
そうなると分子が0か1しかとらない形になるので常に0になっちゃう気がするけど…orz
振る舞いポリシーの方はたぶん ε-greedy になるので以下になるかと思います(?)
\mu(\alpha|s) = \left\{
\begin{array}{ll}
\epsilon/N + 1 - \epsilon \quad (argmax_{\alpha \in A} Q(s, \alpha)) \\
\epsilon/N \quad (otherwise)
\end{array}
\right.
ここで N はアクション数。
sliding-window UCB法(追記:2020/7/15)
何か忘れていると思ったらUCB法の実装の記述を忘れていましたので追記しておきます。
UCB値は以下の数式で算出します。
$$ N_k(a) = \sum_{m=0}^{k-1} 1 (A_m = a) $$
\hat{\mu}_k(a) = \frac{1}{N_k(a)} \sum_{m=0}^{k-1} R_k(a)1 (A_m = a)
A_k = argmax_{1\leq a \leq N} \hat{\mu}_{k-1}(a) + \beta \sqrt{ \frac{ log(k-1) }{N_{k-1}(a)} }
$A$が各アームを表し、$k$がエピソード回数(windowサイズは超えない)で、$R$が報酬、$\beta$はUCBの定数です。
またεの確率で、UCB法で選択するかランダムに選択するかを選びます。
#--- define
ucb_data = [] # 履歴保存用
ucb_window_size = 90 # 上限
policy_num = 32 # ポリシーの総数
ucb_beta = 1 # UCBのβ
ucb_epsilon = 0.5 # εでUCBを使うか選択
#--- local val
episode_count = 0 # エピソード数
gamma_list = create_gamma_list_agent57(policy_num) # 割引率を計算
def reset_states(self):
# 毎エピソードの最初のタイミング
if not training:
# traningじゃない場合はpolicy0(=探索なし)
policy_index = 0
else:
if episode_count > 0:
# UCB計算用に前回の選んだポリシーと取得した報酬を保存
ucb_data.append([policy_index, total_reward])
if len(ucb_data) >= ucb_window_size:
ucb_data.pop(0)
if episode_count < policy_num:
# 全て1回は実行
policy_index = episode_count
else:
r = random.random()
if r < ucb_epsilon:
# ランダムでpolicyを決定
policy_index = random.randint(0, policy_num-1) # a <= n <= b
else:
# UCB値を計算
N = [1 for _ in range(policy_num)]
u = [0 for _ in range(policy_num)]
for d in ucb_data:
N[d[0]] += 1
u[d[0]] += d[1]
for i in range(policy_num):
u[i] /= N[i]
count = len(ucb_data)
k = [0 for _ in range(policy_num)]
for i in range(policy_num):
k[i] = u[i] + ucb_beta * np.sqrt(np.log(count)/N[i])
# 最大のUCB値のポリシー
policy_index = np.argmax(k)
# エピソード回数+1
episode_count += 1
# ポリシーに応じた割引率を設定
gamma = gamma_list[policy_index]
あとがき
LSTMまわりとかキューに関してとか並列処理とか細かいところは説明しきれていません。。。
ソースコードは公開しているので細かい部分はそちらで確認してください。
これで強化学習のアルゴリズムとして1つの目標に到達した感はありますが、まだまだ改善の余地はあると思います。
一番改善してほしいのはなんといっても要求スペックですね。
R2D2の頃からそうでしたが論文内ではActor数は512となっています。
私のPCでは2、多くても4が限界です…(CPUが1つしかないのもありますが)
次の新しい手法に期待ですね。