ここら辺から自分の理解が追い付かなくなりつつあります。
ネット上の情報をかき集めて実装しているので正確ではないところがある点はご了承ください。
(違う個所はご指摘いただけると幸いです)
本シリーズ
- 【強化学習】OpenAI Gym×Keras-rlで強化学習アルゴリズムを実装していくぞ(準備編)
- 【強化学習】OpenAI Gym×Keras-rlで強化学習アルゴリズムを実装していくぞ(Q学習編)
- 【強化学習】OpenAI Gym×Keras-rlで強化学習アルゴリズムを実装していくぞ(DQN編)
- 【強化学習】Keras-rlでRainbowを実装/解説(ここ)
- 【強化学習】Keras-rlでApe-Xを実装/解説(並列プログラミング)
- MNISTでSaliencyMapとGrad_CAMを試してDQN(DuelingNetwork)を可視化してみた(実装/解説)
- 【強化学習】2018年度最強と噂のR2D2を実装/解説してみた
- 【強化学習】複数の探索ポリシーを実装/解説して比較してみた
- 【強化学習】DQNのハイパーパラメータを3つのゲームで比較してみた
- 【強化学習】R2D2を実装/解説してみたリベンジ 解説編(Keras-RL)
- 【強化学習】R2D3を実装/解説してみた(Keras-RL)
- 【強化学習】ついに人間を超えた!?Agent57を解説/実装してみた(Keras-RL)
追記:改めて記事にしています。
概要
- Rainbow の7種類ある手法のうち6種類を実装。
- Double DQNの解説/実装
- Priority Experience Reply(優先順位付き経験再生)の解説/実装
- Dueling Networkの解説/実装
- Multi-Step learningの解説/実装
- Noisy Networkの実装
※2019/06/13:PERのRankBaseについて加筆しました。
コード全体
本記事で作成したコードは以下です。
※1ファイル完結です。
※GoogleColaboratoryは実行結果付き
- ほぼRainbowAgentのコード(画像なし学習版と画像あり学習版)(GitHubGist)
- ほぼRainbowAgentのコード(画像なし学習版と画像あり学習版)(GoogleColaboratory)
Rainbowについて
Rainbow は DQN 以降に登場したいろいろな改良を全部乗せしたアルゴリズムです。
7種類あるので Ranbow なのでしょう。
今回の実装ですが、投稿者の理解が足りず6種類までとなります。すいません。
また、keras-rl 公式で実装されているのは DoubleDQN と Dueling Network のみなのでこれで一応意味のあるコードになるかと…
Rainbowに関してはここのスライドがとても分かりやすいです。
DQNからRainbowまで 〜深層強化学習の最新動向〜
Double DQN
DQNではアクションで最大のQ値を選んでいますが、最大のQ値が(ノイズ等の影響で)過大評価されている可能性があります。
過大評価されたQ値ばかりを伝搬させるのはよろしくないとのことで提案された手法がDoubleDQNです。
(個人的にはアクションの選択で解決すべき問題な気もしますが…)
概要ですがDQNではQ値の更新に、次の状態の TargetNetwork の最大Q値を用いていましたが、
DDQNでは、QNetworkの最大Q値のアクションにおける TargetNetwork を用います。
要するに状態SのQ値が以下だった場合、
TargetNetwok[S][0] = 0.1
TargetNetwok[S][1] = 0.2
TargetNetwok[S][2] = 0.3
QNetwok[S][0] = 0.3
QNetwok[S][1] = 0.2
QNetwok[S][2] = 0.1
DQNではQ値が最大である TargetNetwok[S][2] = 0.3 が選ばれますが、
DDQNでは QNetowrk が最大の 0 アクションを選び、Q値としては TargetNetwork[S][0] = 0.1 が選ばれます。
(この選出はQ値の更新時のみです)
参考
・CartPoleでDQN(deep Q-learning)、DDQNを実装・解説【Phythonで強化学習:第2回】
・【強化学習初心者向け】シンプルな実装例で学ぶQ学習、DQN、DDQN【CartPoleで棒立て:1ファイルで完結、Kearas使用】
・Let’s make a DQN: Double Learning and Prioritized Experience Replay
・introduction to double deep Q-learning
実装
前回のDQN編のコードを改変していく形で実装していきます。
変更箇所は forward 関数のQ値を更新する箇所です。
import rl.core
class RainbowAgent(rl.core.Agent):
def forward_train(self, observation):
(省略)
batchs = self.memory.sample(self.batch_size)
state0_batch = []
action_batch = []
reward_batch = []
state1_batch = []
for batch in batchs:
state0_batch.append(batch[0])
action_batch.append(batch[1])
reward_batch.append(batch[2])
state1_batch.append(batch[3])
# 更新用に現在のQネットワークを出力(Q network)
outputs = self.model.predict(np.asarray(state0_batch), self.batch_size)
if self.enable_double_dqn:
# TargetNetworkとQNetworkのQ値を出す
state1_model_qvals_batch = self.model.predict(np.asarray(state1_batch), self.batch_size)
state1_target_qvals_batch = self.target_model.predict(np.asarray(state1_batch), self.batch_size)
for i in range(self.batch_size):
action = np.argmax(state1_model_qvals_batch[i]) # modelからアクションを出す
maxq = state1_target_qvals_batch[i][action] # Q値はtarget_modelを使って出す
td_error = reward_batch[i] + self.gamma * maxq
outputs[i][action_batch[i]] = td_error # 更新
else:
(前回のDQNの実装)
# Q networkの学習
self.model.train_on_batch(np.asarray(state0_batch), np.asarray(outputs))
enable_double_dqn はハイパーパラメータでDDQNを使うかどうかを選択できるようにしています。
def __init__(self, enable_double_dqn=False):
self.enable_double_dqn = enable_double_dqn
Priority Experience Reply(優先順位付き経験再生)
今回で一番重い解説です。
直感でわかると思いますが経験には学習しやすい経験と学習しにくい経験があると思います。
DQNの Experience Reply(経験再生) ではランダムなのでそういった区別がありません。
そこで学習しやすい経験=TD誤差が大きい経験として優先順位をつけたのが Priority Experience Reply(優先順位付き経験再生) です。
参考
・Let’s make a DQN: Double Learning and Prioritized Experience Replay
・【深層強化学習】優先順位付き経験再生 ( Prioritized Experience Replay ) 実装・解説
・【強化学習中級者向け】実装例から学ぶ優先順位付き経験再生 prioritized experience replay DQN 【CartPoleで棒立て:1ファイルで完結】
・pytorchでprioritized experience replyを実装
・【論文】Prioritized Experience Replay (2016)
・Prioritized Experience Replay
Greedy TD-error prioritization
概要
大きく分けて3種類の方法があります。
まずは一番シンプルなTD誤差が最大の経験を優先する場合です。
TD誤差を $\delta_{t}$ で表現しておきます。
$$DQN: \delta_{t} = r_{t} + \gamma \max_pQ_{target}(s_{t+1,p}) - Q(s_{t},a_{t})$$
$$DDQN: \delta_{t} = r_{t} + \gamma Q_{target}(s_{t+1,\max_pQ(s_{t+1},p)}) - Q(s_{t},a_{t})$$
実装(memory側)
ヒープ木が推奨されているようなので使います。
python の heapq では == で比較できないオブジェクトでエラーがでるようなので wrapper で回避しています。
参考:Adding numpy array to a heap queue
import heapq
class _head_wrapper():
def __init__(self, data):
self.d = data
def __eq__(self, other):
return True
class PERGreedyMemory():
def __init__(self, capacity):
self.buffer = []
self.capacity = capacity
self.max_priority = 1
def add(self, experience):
if self.capacity <= len(self.buffer):
# 上限より多い場合は最後の要素を削除
self.buffer.pop()
# priority は最初は最大を選択
experience = _head_wrapper(experience)
heapq.heappush(self.buffer, (-self.max_priority, experience))
def update(self, experience, td_error):
# heapqは最小値を出すためマイナス
experience = _head_wrapper(experience)
heapq.heappush(self.buffer, (-td_error, experience))
# 最大値を更新
if self.max_priority < td_error:
self.max_priority = td_error
def sample(self, batch_size):
# 取り出す(学習後に再度追加)
batchs = [heapq.heappop(self.buffer)[1].d for _ in range(batch_size)]
return batchs
wrapperですが、data はデータを保持すればいいので適当です。
__eq__が heapq 用となります。
import heapq
class _head_wrapper():
def __init__(self, data):
self.d = data
def __eq__(self, other):
return True
add関数は最初の追加で実行されることを想定しています。
最初に許容量を比較し、超えている場合は buffer の最後を削除しています。
buffer はヒープ木となっているため、最後はTD誤差の小さい値になっています。
また、最初の priority は経験を1回は必ず選ばれてほしいので現在保持している中で最大の優先度にします。
マイナスで heapq に代入しているのは heapq が最小値を先頭にするからです。
update も同様です。
td_error を priority として追加しています。
最後に sample 関数です。
batch_size 分取り出します。
def sample(self, batch_size, step):
# 取り出す(学習後に再度追加)
batchs = [heapq.heappop(self.buffer)[1].d for _ in range(batch_size)]
return batchs
priority の更新は heapq の pop/push で実現しています。
もっといい方法がありそうですがとりあえず…
実装(agent側)
まずは memory クラスを置き換えます。
def __init___(self):
(略)
#self.memory = ReplayMemory(memory_capacity)
self.memory = PERGreedyMemory(memory_capacity)
次に forward_train の更新後に update を追加します。
update は DQN、DDQN 両方の箇所で追加しますが内容は同じです。
def forward_train(self):
(略)
# ここはそのまま
self.memory.add(
(self.recent_observations[:self.window_length],
self.recent_action,
self.recent_reward,
self.recent_observations[1:])
)
(略)
# ここもそのまま
batchs = self.memory.sample(self.batch_size, self.step)
state0_batch = []
action_batch = []
reward_batch = []
state1_batch = []
(略)
for i in range(self.batch_size):
action = np.argmax(state1_model_qvals_batch[i])
maxq = state1_target_qvals_batch[i][action]
td_error = reward_batch[i] + self.gamma * maxq
# 追加箇所:TD誤差を取得
td_error_diff = outputs[i][action_batch[i]] - td_error
outputs[i][action_batch[i]] = td_error
# 追加箇所:TD誤差を更新
self.memory.update(batchs[i], td_error_diff)
Proportional Prioritization
greedy TD-error prioritization は最大値のみ学習していくのでノイズ等の影響が大きくうまく学習できない問題がありました。
そこで確率的なサンプリングをする手法が2種類提案されています。
まずは Proportional からです。
概要
Proportional Prioritization(比例優先順位付け) はTD誤差が大きいものほど高確率で選ばれるという考えです。
まずある経験がとる優先度は以下です。
$$p_{t} = |\delta_{t}|+\epsilon$$
$\delta_{t}$ はTD誤差ですね。
$\epsilon$ は0にならないようにするための小さい値(定数)です。
これを元に確率は以下となります。
$$P_{t} = \frac{ p_{t}^\alpha}{\sum_k p_{k}^\alpha} $$
$k$ はメモリの最大サイズとなります。
$\alpha$ はハイパーパラメータとなり(0.0~1.0)、この確率の適用率となります。
0なら Greedy TD-error と同様で(最大値を選択)、1なら Proportional Prioritization に準拠します。
0 なら完全ランダム(ReplayMemoryと同様)、1なら Proportional Prioritization ですね。
実装(memory側)
確率の計算をもう少し詳細に話します。
具体例で、メモリに経験が以下の4つ入っていたとします。
| index | priority |
|---|---|
| 0 | 0.1 |
| 1 | 0.2 |
| 2 | 0.3 |
| 3 | 0.4 |
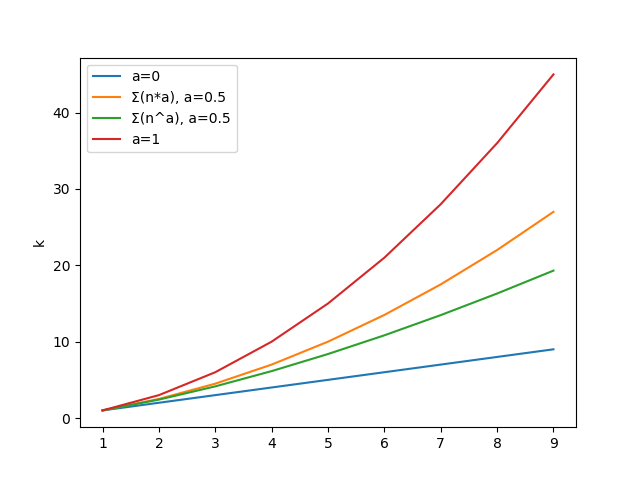
$\alpha = 0.5$ とした場合、$\sum_k p_{k}^\alpha$ は $0.1^{0.5} + 0.2^{0.5} + 0.3^{0.5} + 0.4^{0.5} = 1.94361945106$ です。
各確率は以下の通りです。
| index | priority | ^α | 確率 |
|---|---|---|---|
| 0 | 0.1 | 0.31622776601 | 0.16270045344 |
| 1 | 0.2 | 0.4472135955 | 0.23009318787 |
| 2 | 0.3 | 0.5477225575 | 0.28180545178 |
| 3 | 0.4 | 0.63245553203 | 0.32540090689 |
こういったアルゴリズムは重み付きランダムサンプリングっていうのでしょうか。
参考:重み付きランダムサンプリングアルゴリズム
問題は処理で、add → sample → update → add → sample → update という順番となり、毎回確率の計算をする必要がある点です。
要するに追加/更新/サンプリングにおいて、O(N) の計算が発生するとすごく遅くなります。
(Nはメモリの最大値)
Proportional に関してはこのブログで SumTree という方法が記載されており、今回はそれをそのまま使います。
この方法の解説は省きます。(興味のある方は元ブログの方へ)
まずは SumTree です。
コピペしています。
#copy from https://github.com/jaromiru/AI-blog/blob/5aa9f0b/SumTree.py
import numpy
class SumTree:
write = 0
def __init__(self, capacity):
self.capacity = capacity
self.tree = numpy.zeros( 2*capacity - 1 )
self.data = numpy.zeros( capacity, dtype=object )
def _propagate(self, idx, change):
parent = (idx - 1) // 2
self.tree[parent] += change
if parent != 0:
self._propagate(parent, change)
def _retrieve(self, idx, s):
left = 2 * idx + 1
right = left + 1
if left >= len(self.tree):
return idx
if s <= self.tree[left]:
return self._retrieve(left, s)
else:
return self._retrieve(right, s-self.tree[left])
def total(self):
return self.tree[0]
def add(self, p, data):
idx = self.write + self.capacity - 1
self.data[self.write] = data
self.update(idx, p)
self.write += 1
if self.write >= self.capacity:
self.write = 0
def update(self, idx, p):
change = p - self.tree[idx]
self.tree[idx] = p
self._propagate(idx, change)
def get(self, s):
idx = self._retrieve(0, s)
dataIdx = idx - self.capacity + 1
return (idx, self.tree[idx], self.data[dataIdx])
次に memory 側です。
class PERProportionalMemory():
def __init__(self, capacity, alpha):
self.capacity = capacity
self.tree = SumTree(capacity)
self.alpha = alpha
self.max_priority = 1
def add(self, experience):
・SumTreeに追加
def update(self, index, experience, td_error):
・SumTreeの更新
if self.max_priority < priority:
self.max_priority = priority
def sample(self, batch_size, step):
・サンプリング
SumTree の追加部分です。
最初はpriority最大で追加します。
def add(self, experience):
self.tree.add(self.max_priority, experience)
SumTree の更新部分です。
priority を計算して追加しています。
def update(self, index, experience, td_error):
priority = (abs(td_error) + 0.0001) ** self.alpha
self.tree.update(index, priority)
サンプリング部分です。
順番に見ていきます。
まずは初期化です。
indexes が今回選んだあとの SumTree 上のindexになります。
batchs が選ばれた経験です。
def sample(self, batch_size):
indexes = []
batchs = []
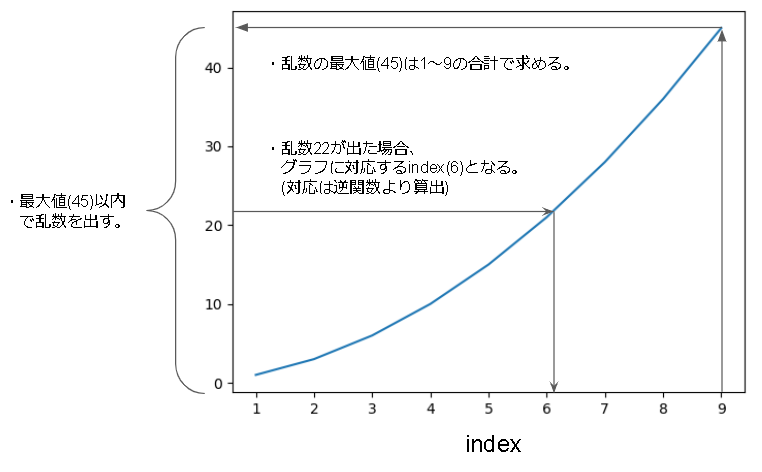
使い方ですが、SumTree はある数字を渡すとその数字に該当する要素を返してくれます。
今回は batch_size 分を重複なくほしいので total を区間で割りその区間内からランダムで数字を渡す事で重複のないサンプリングを実現します。
例えば total が 100 で batch_size が 4 だった場合、区間を 0~25, 26~50 ,51~75, 76~100 とします。
その区間内でそれぞれ乱数を出します。例えば 2, 29, 60, 88 です。
その数字を SumTree に渡すと対応するデータが取得できます。
# 合計を均等に割り、その範囲内からそれぞれ乱数を出す。
total = self.tree.total()
section = total / batch_size
for i in range(batch_size):
r = section*i + random.random()*section
(idx, priority, experience) = self.tree.get(r)
indexes.append(idx)
batchs.append(experience)
return (indexes ,batchs)
実装(agent側)
引数と戻り値が少し変わっているので変えます。
per_alpha はハイパーパラメータです。
def __init___(self, per_alpha=0.6):
(略)
#self.memory = ReplayMemory(memory_capacity)
#self.memory = PERGreedyMemory(memory_capacity)
self.memory = PERProportionalMemory(memory_capacity, per_alpha)
forward_train 側です。
def forward_train(self):
(略)
# sample の戻り値を追加
(indexes, batchs) = self.memory.sample(self.batch_size)
state0_batch = []
action_batch = []
reward_batch = []
state1_batch = []
(略)
for i in range(self.batch_size):
(略)
# update にindexを追加
self.memory.update(indexes[i], batchs[i], td_error_diff)
RankBase Prioritization
確率的サンプリングの2つ目です。
RankBase は順位を元に確率を決めます。
まずは Priority からです。
概要
$p$ が違うだけで他は Proportional と同じです。
$$priority_{t} = |\delta_{t}|+\epsilon$$
$$p_{t} = \frac{1}{rank(i)}$$
※$rank$ は $priority$ のメモリ内順位
実装(memory側)
いい方法が見つからず…orz
とりあえずのO(N)実装です。(メモリサイズを増やすと遅い…)
bisect を使うので wrapper を作成します。
import bisect
class _bisect_wrapper():
def __init__(self, data):
self.d = data
self.priority = 0
self.p = 0
def __lt__(self, o): # a<b
return self.priority > o.priority
メモリ側です。
class PERRankBaseMemory():
def __init__(self, capacity, alpha):
self.capacity = capacity
self.buffer = []
self.alpha = alpha
self.max_priority = 1
def add(self, experience):
if self.capacity <= len(self.buffer):
# 上限より多い場合は最後の要素を削除
self.buffer.pop()
experience = _bisect_wrapper(experience)
experience.priority = self.max_priority
bisect.insort(self.buffer, experience)
def update(self, index, experience, td_error):
priority = (abs(td_error) + 0.0001) # priority を計算
experience = _bisect_wrapper(experience)
experience.priority = priority
bisect.insort(self.buffer, experience)
if self.max_priority < priority:
self.max_priority = priority
def sample(self, batch_size, step):
・サンプリング
add と update の解説は省略します。
bisect を使って追加しているだけです。
sampleです。まずは初期化。
def sample(self, batch_size):
indexes = []
batchs = []
Rankに従って確率とtotalを出します。
total = 0
for i, o in enumerate(self.buffer):
o.index = i
o.p = (len(self.buffer) - i) ** self.alpha
total += o.p
o.p_total = total
Proportional と同じ考えで、区間から抽選しています。
# 合計を均等に割り、その範囲内からそれぞれ乱数を出す。
index_lst = []
section = total / batch_size
rand = []
for i in range(batch_size):
rand.append(section*i + random.random()*section)
rand_i = 0
for i in range(len(self.buffer)):
if rand[rand_i] < self.buffer[i].p_total:
index_lst.append(i)
rand_i += 1
if rand_i >= len(rand):
break
最後に取得です。
Greedy と同様に sample で pop し、update で push する形を採用しています。
for i, index in enumerate(reversed(index_lst)):
o = self.buffer.pop(index) # 後ろから取得するのでindexに変化なし
batchs.append(o.d)
indexes.append(index)
return (indexes ,batchs)
実装(agent側)
PERProportionalMemory を変えるだけで行けます。
def __init___(self, per_alpha=0.6):
(略)
#self.memory = ReplayMemory(memory_capacity)
#self.memory = PERGreedyMemory(memory_capacity)
#self.memory = PERProportionalMemory(memory_capacity, per_alpha)
self.memory = PERRankBaseMemory(memory_capacity, per_alpha)
2019/6/13 追記:O(1)によるRankBaseの実装
探せばあるかもしれませんが、特に参考文献はありません。
基本アイデアは Rank で Priority がつくということは等差数列で全要素の確率を計算できるというものです。
(わざわざ全部走査しなくていい)
ただ、ネックとなっているのは確率の適用率を表す$\alpha$で、これを指数で適用すると等差数列になりません。
そこで$\alpha$を思い切って比率に変えて等差数列を適用させます。
各確率は等差数列の公式から以下です。
$$ p_{n} = 1 + (n-1)\alpha $$
合計は以下。
$$ S_k = \sum_k \alpha p_{k} = \frac{k(2 + (k-1)\alpha)}{2} $$
これに変えた場合の誤差は以下です。
(合計を比較しています)
$\alpha=0$ と $\alpha=1$ では同じ結果になります。
$\alpha=0.5$ では比率のほうが強く反映される結果ですね。
次にランダムサンプリングですが、以下のように最大値から乱数をだし、逆算して要素を取得する方法をとります。
逆算するために逆関数を出します。
$$ S^{-1}_k = \frac{\alpha-2+\sqrt{(2-\alpha)^2 + 8\alpha k}}{2\alpha} $$
※$\alpha=0$ の時 $S^{-1}_k=k$
python だと以下となります。
import math
def rank_sum(k, a):
return = k*( 2+(k-1)*a )/2
def rank_sum_inverse(k, a):
if a == 0:
return k
t = a-2 + math.sqrt((2-a)**2 + 8*a*k)
return t/(2*a)
PERRankBaseMemory の sample 関数を書き換えます。
def sample(self, batch_size):
indexes = []
batchs = []
# 合計値をだす
total = rank_sum(len(self.buffer)+1, self.alpha)
# index_lst
index_lst = []
for _ in range(batch_size):
# index_lstにないものを追加
for _ in range(100): # for safety
r = random.random()*total
index = rank_sum_inverse(r, self.alpha)
index = int(index) # 整数にする(切り捨て)
if index not in index_lst:
index_lst.append(index)
break
assert len(index_lst) == batch_size
index_lst.sort()
# batchs を用意
for i, index in enumerate(reversed(index_lst)):
o = self.buffer.pop(index) # 後ろから取得するのでindexに変化なし
batchs.append(o.d)
indexes.append(index)
return (indexes ,batchs)
重要度サンプリング(IS: Importance Sampling)
サンプリングに優先順位がついたのでサンプリングの分布に偏りが生じてしまい、学習する値が偏ってしまう。
そこでその偏りを修正するのが重要度サンプリングとのこと。
(よくわかっていない)
Q学習の重みの更新の際、TD誤差 $\delta_{i}$ ではなく、重み付けした $\delta_{i}・w_{i}$ を使うことで実装される。
wiは下記で定義される。
$$w_{i} = (N*P_{i})^{-\beta}$$
N はメモリの最大値です。
$\beta$ は修正の度合いを決める指数で 0 でISなし、1 で最大の偏り修正となります。
また、学習の偏り修正は学習後半で重要だが前半は重要ではないので、$\beta$は学習の終わりで1になるように線形に大きくしていきます。
また、安定性のために $\frac{1}{max_{w_{i}}}$で正規化します。
実装(memory側)
ハイパーパラメータが増えます…
この実装は、PERRankBaseMemory と PERProportionalMemory で同じ実装となります。
def __init__(self, beta_initial=0.0, beta_steps=10000, enable_is):
(略)
self.beta_initial = beta_initial
self.beta_steps = beta_steps
self.enable_is = enable_is
beta_initial が$\beta$の初期値
beta_steps が$\beta$が1になるまでのstep数
enable_is が重要度サンプリングを無効/有効にするフラグです。
次に sample です。引数に step を追加してます。
def sample(self, batch_size, step):
# weights用の変数を用意
weights = np.empty(batch_size, dtype='float32')
if self.enable_is:
# βは最初は低く、学習終わりに1にする。
beta = self.beta_initial + (1 - self.beta_initial) * step / self.beta_steps
(略)
buffer_size = 現在の配列のサイズ
for i, index in enumerate(reversed(index_lst)):
(バッチデータを取得する処理)
if self.enable_is:
# 重要度サンプリングを計算
priority = 取得したbatchのpriority
weights[i] = (buffer_size * priority / total) ** (-beta)
else:
weights[i] = 1 # 無効なら1
if self.enable_is:
# 安定性の理由から最大値で正規化
weights = weights / weights.max()
# weights も返す
return (indexes ,batchs, weights)
実装(agent側)
td_error に weight を掛けるだけです。
def forward_train(self):
(略)
# step を引数に追加し、戻り値に weights を追加
(indexes, batchs, weights) = self.memory.sample(self.batch_size, self.step)
state0_batch = []
action_batch = []
reward_batch = []
state1_batch = []
(略)
for i in range(self.batch_size):
action = np.argmax(state1_model_qvals_batch[i])
maxq = state1_target_qvals_batch[i][action]
td_error = reward_batch[i] + self.gamma * maxq
# td_error に weights をかける
td_error *= weights[i]
td_error_diff = outputs[i][action_batch[i]] - td_error
outputs[i][action_batch[i]] = td_error
self.memory.update(indexes[i], batchs[i], td_error_diff)
ハイパーパラメータ化
最後にメモリを選べるようにハイパーパラメータ化します。
def __init___(self, memory_type="replay"):
(略)
#self.memory = ReplayMemory(memory_capacity)
#self.memory = PERGreedyMemory(memory_capacity)
#self.memory = PERProportionalMemory(memory_capacity, per_alpha)
self.memory = PERRankBaseMemory(memory_capacity, per_alpha)
↓
if memory_type == "replay":
self.memory = ReplayMemory(memory_capacity)
elif memory_type == "per_greedy":
self.memory = PERGreedyMemory(memory_capacity, per_alpha, per_beta_initial, per_beta_steps, per_enable_is)
elif memory_type == "per_proportional":
self.memory = PERProportionalMemory(memory_capacity, per_alpha, per_beta_initial, per_beta_steps, per_enable_is)
elif memory_type == "per_rankbase":
self.memory = PERRankBaseMemory(memory_capacity, per_alpha, per_beta_initial, per_beta_steps, per_enable_is)
else:
raise ValueError('memory_type is ["replay","per_greedy","per_proportional","per_rankbase"]')
各メモリまとめ
今回実装したメモリの一覧です。
n がメモリの最大値です。
| データ構造 | add | sample | update | 上限を超えた場合の削除処理 | |
|---|---|---|---|---|---|
| ReplayMemory | RingBuffer | $O(1)$ | random.sampleの速さ | $0$ ※更新なし | 古い順に削除 |
| PERGreedyMemory | 二分ヒープ | $O(log(n))$ | $O(1)$ | $O(log(n))$ ※addで実装 | TD誤差が低いのから削除 |
| PERProportionalMemory | 二分ヒープ | $O(log(n))$ | $O(log(n))$ ※木を降りて取得 | $O(log(n))$ ※木を登って更新 | 古い順に削除 |
| PERRankBaseMemory | ソート済み配列 | $O(n)$ ※2分探索 | $O(n)$ ※確率計算で1順 | $O(n)$ ※addで実装 | TD誤差が低いのから削除 |
| PERRankBaseMemory(改良) | ソート済み配列 | $O(n)$ ※2分探索 | $O(1)+O(n)$ ※数式で算出 | $O(n)$ ※addで実装 | TD誤差が低いのから削除 |
※2022/6/5大きく間違っていたのでオーダーのみ修正
Dueling Network
DQNとの違いを表した画像です。

上のネットワークが今までの Q-Network で行動価値関数 $Q(s,a)$ を最後に出力します。
それを下のように途中で状態価値関数 $V(s)$ と Advantage関数 $A(s,a)$ に分けて合成させて $Q(s,a)$ を予測するネットワークが Dueling Network になります。
$V(a)$ が行動$a$によらずに学習できる事が大きな利点とのことです。
参考
【強化学習中級者向け】実装例から学ぶDueling Network DQN 【CartPoleで棒立て:1ファイルで完結】
【深層強化学習】Dueling Network 実装・解説
Dueling Network Architectures for Deep Reinforcement Learning
keras-rlのdqnのgithubコード
実装
ネットワークの中身の実装に目をつぶれば置き換えるだけなので簡単です。
また、この実装は Sequential モデルでは実現できませんね。
Flatten 後のネットワークを置き換えていきます。
def build_network(self):
(省略)
c = Flatten()(c)
# Dueling Network を使うかどうかを切り替えれるハイパーパラメータです。
if self.enable_dueling_network:
# value
v = Dense(512, activation="relu")(c)
v = Dense(1)(v)
# advance
adv = Dense(512, activation='relu')(c)
adv = Dense(self.nb_actions)(adv)
# 連結で結合
c = Concatenate()([v,adv])
c = Lambda(lambda a: K.expand_dims(a[:, 0], -1) + a[:, 1:] - K.mean(a[:, 1:], axis=1, keepdims=True), output_shape=(self.nb_actions,))(c)
else:
# 使わない場合はただのfc
c = Dense(512, activation="relu")(c)
c = Dense(self.nb_actions, activation="linear")(c) # 出力層
return Model(input_, c)
value と advance の箇所は簡単だと思います。
それぞれ Flatten の出力から全結合しています。
モデルのパラメータは論文に沿っています。
2つの value,advance に対して Concatenate で結合しています。
Concatenate は keras の Merge レイヤーと呼ばれるもので、複数のレイヤーを結合してくれます。
Concatenate したレイヤーを Lambda レイヤーに渡します。
Lambda レイヤーも keras の特殊な層で、変わった Model を実装するときに使うそうです。
参考:Kerasでちょっと難しいModelやTrainingを実装するときのTips
Lamdba レイヤーの中身を詳細に見ていきます。
c = Lambda(
lambda a:
K.expand_dims(a[:, 0], -1) + a[:, 1:] - K.mean(a[:, 1:], axis=1, keepdims=True),
output_shape=(self.nb_actions,)
)(c)
まず Lambda レイヤーは、Lambda(関数, output_shape) をとります。
output_shape は出力形式なのでここではアクション数ですね。
関数ですが、第1引数に入力テンソルが入ってきます。
この入力テンソルには配列のスライス表記が使えるので便利です。
ただ、batch_size が含まれている点は注意が必要です。
例えば入力10の要素を5個ずつ分割したい場合は以下のような記載になります。
inputs = Input((10, ))
x0_4 = Lambda(lambda x: x[:, :5], output_shape=(5,) )(inputs)
x5_9 = Lambda(lambda x: x[:, 5:], output_shape=(5,) )(inputs)
d1 = Dense(10)(x0_4)
d2 = Dense(10)(x5_9)
x[:, :5] で前半の5個、x[:, 5:] で後半の5個を取得しています。
さて、戻って lamdba 関数の中を順番に見ていきます。
K.expand_dims(a[:, 0], -1)
上記ですが、入力は V と advance を Concatenate で連結したものなので、a[:, 0] は V になります。
K.expand_dims で次元を追加し元の形に合わせています。
a[:, 1:]
上記は、advance を取り出しているだけですね。
K.mean(a[:, 1:], axis=1, keepdims=True)
これは、advance の平均値を取得しています。
この平均は、状態価値関数と advantage 関数を識別しやすくするために導入されているものらしく、平均値の代わりに最大値を使ったり特に何もしなかったりといった実装があるっぽいです。
(詳細は論文を見てください)
今回は平均値で実装しています。
最後にこれらを計算します。
ざっくり書くと、$V + advance - 平均(advance)$ です。
lambda a:
K.expand_dims(a[:, 0], -1) + a[:, 1:] - K.mean(a[:, 1:], axis=1, keepdims=True),
最後にハイパーパラメータを忘れずに追加しておきます。
def __init__(self, enable_dueling_network=False):
self.enable_dueling_network = enable_dueling_network
Multi-Step learning
通常は1step分の報酬を使うが n-step 分の報酬を使おうという内容。
報酬は n-step 分に合わせて$\gamma$(割引率)分減らします。
$$DQN : TDerror = r_t + \gamma \max_pQ_{target}(s_{t+1,p}) - Q(s_{t},a_{t}) $$
$$n_{step}DQN : TDerror = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + ... + \gamma^{n-1} r_{t+n-1} + \gamma^n \max_pQ_{target}(s_{t+n,p}) - Q(s_{t},a_{t}) $$
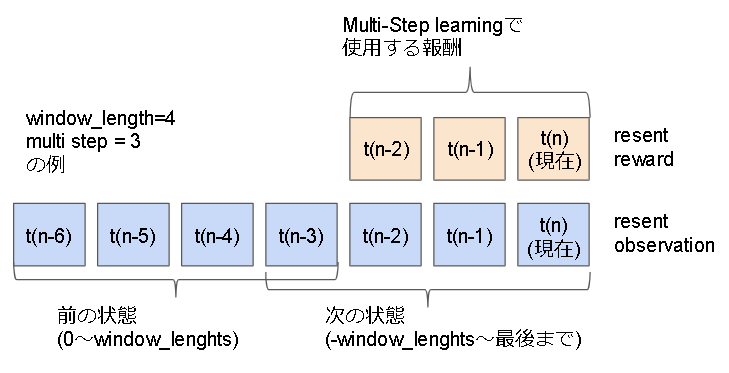
実装はこんなイメージで実装しています。
参考
pytorchでmulti step learningを実装
【深層強化学習】Ape-X 実装・解説
実装
まずはハイパーパラメータの追加。
def __init__(self, multireward_steps=3):
self.multireward_steps= multireward_steps
初期化部分を書き換え。
def reset_states(self):
(略)
self.recent_reward = 0
self.recent_observations = [np.zeros(self.input_shape) for _ in range(self.window_length+1)]
↓
self.recent_reward = [0 for _ in range(self.multireward_steps)]
self.recent_observations = [np.zeros(self.input_shape) for _ in range(self.window_length+self.multireward_steps)]
recent_reward は配列にし、recent_observations の確保数を1から multistep のサイズに拡張しています。
報酬の追加部分を書き換えます。
def backward(self, reward, terminal):
self.recent_reward = reward
↓
self.recent_reward.append(reward) # 最後に追加
self.recent_reward.pop(0) # 先頭を削除
(省略)
return []
計算はメモリの追加部分で計算します。
def forward_train(self):
if not self.training:
return
# 報酬を割引しつつ加算する。
reward = 0
for i, r in enumerate(self.recent_reward):
reward += r * (self.gamma ** i)
# memoryに追加
self.memory.add(
(self.recent_observations[:self.window_length],
self.recent_action,
reward,
self.recent_observations[1:])
)
↓ recent_observations の取り方が変わったので合わせて変えています。
self.memory.add(
(self.recent_observations[:self.window_length],
self.recent_action,
reward,
self.recent_observations[-self.window_length:])
)
(省略)
TD誤差計算の所も修正
def forward_train(self):
(省略)
td_error = reward_batch[i] + self.gamma * maxq
↓
td_error = reward_batch[i] + (self.gamma ** self.multistep_reward) * maxq
(省略)
最後に行動選択の所でも recent_observations を参照しているので、そこも忘れずに修正。
def forward(self):
(省略)
if self.step % self.action_interval == 0:
if self.training:
(ϵ-greedy法 でアクションを決定)
else:
# 現在の状態を取得し、最大Q値から行動を取得。
state0 = self.recent_observations[1:]
q_values = self.model.predict(np.asarray([state0]), batch_size=1)[0]
action = np.argmax(q_values)
↓
state0 = self.recent_observations[-self.window_length:]
q_values = self.model.predict(np.asarray([state0]), batch_size=1)[0]
action = np.argmax(q_values)
(省略)
Noisy Network
探索アプローチとして ϵ-greedy法 を使っているが不十分である。
そこでネットワークの重みに摂動を加えることでより複雑で長期的な探索に対応できるとのこと。
アイデアメモ
個人的にはQ学習からここはアイデアがあり、ϵ-greedy法よりバンデッドアルゴリズムを用いるべきではないかと思っています。
Q学習もϵ-greedy法よりUCBアルゴリズムを適用したほうが精度がいいと思っています。
最新手法に追いついたらここら辺は応用してみたいです。
実装
正直実装がよくわかりませんでした。
以下のコードを使わせてもらっています。
#copy from https://github.com/OctThe16th/Noisy-A3C-Keras
class NoisyDense(Layer):
def __init__(self, units,
sigma_init=0.02,
activation=None,
use_bias=True,
kernel_initializer='glorot_uniform',
bias_initializer='zeros',
kernel_regularizer=None,
bias_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
bias_constraint=None,
**kwargs):
if 'input_shape' not in kwargs and 'input_dim' in kwargs:
kwargs['input_shape'] = (kwargs.pop('input_dim'),)
super(NoisyDense, self).__init__(**kwargs)
self.units = units
self.sigma_init = sigma_init
self.activation = activations.get(activation)
self.use_bias = use_bias
self.kernel_initializer = initializers.get(kernel_initializer)
self.bias_initializer = initializers.get(bias_initializer)
self.kernel_regularizer = regularizers.get(kernel_regularizer)
self.bias_regularizer = regularizers.get(bias_regularizer)
self.activity_regularizer = regularizers.get(activity_regularizer)
self.kernel_constraint = constraints.get(kernel_constraint)
self.bias_constraint = constraints.get(bias_constraint)
def build(self, input_shape):
assert len(input_shape) >= 2
self.input_dim = input_shape[-1]
self.kernel = self.add_weight(shape=(self.input_dim, self.units),
initializer=self.kernel_initializer,
name='kernel',
regularizer=self.kernel_regularizer,
constraint=self.kernel_constraint)
self.sigma_kernel = self.add_weight(shape=(self.input_dim, self.units),
initializer=initializers.Constant(value=self.sigma_init),
name='sigma_kernel'
)
if self.use_bias:
self.bias = self.add_weight(shape=(self.units,),
initializer=self.bias_initializer,
name='bias',
regularizer=self.bias_regularizer,
constraint=self.bias_constraint)
self.sigma_bias = self.add_weight(shape=(self.units,),
initializer=initializers.Constant(value=self.sigma_init),
name='sigma_bias')
else:
self.bias = None
self.epsilon_bias = None
self.epsilon_kernel = K.zeros(shape=(self.input_dim, self.units))
self.epsilon_bias = K.zeros(shape=(self.units,))
self.sample_noise()
super(NoisyDense, self).build(input_shape)
def call(self, X):
perturbation = self.sigma_kernel * self.epsilon_kernel
perturbed_kernel = self.kernel + perturbation
output = K.dot(X, perturbed_kernel)
if self.use_bias:
bias_perturbation = self.sigma_bias * self.epsilon_bias
perturbed_bias = self.bias + bias_perturbation
output = K.bias_add(output, perturbed_bias)
if self.activation is not None:
output = self.activation(output)
return output
def compute_output_shape(self, input_shape):
assert input_shape and len(input_shape) >= 2
assert input_shape[-1]
output_shape = list(input_shape)
output_shape[-1] = self.units
return tuple(output_shape)
def sample_noise(self):
K.set_value(self.epsilon_kernel, np.random.normal(0, 1, (self.input_dim, self.units)))
K.set_value(self.epsilon_bias, np.random.normal(0, 1, (self.units,)))
def remove_noise(self):
K.set_value(self.epsilon_kernel, np.zeros(shape=(self.input_dim, self.units)))
K.set_value(self.epsilon_bias, np.zeros(shape=self.units,))
NNモデルの最後の層を Dense から変えるだけです。多分。。。
def __init__(self, enable_noisynet):
self.enable_noisynet = enable_noisynet
def build_network(self):
(略)
if self.enable_dueling_network:
# value
v = Dense(512, activation="relu")(c)
if self.enable_noisynet:
v = NoisyDense(1)(v)
else:
v = Dense(1)(v)
# advance
adv = Dense(512, activation='relu')(c)
if self.enable_noisynet:
adv = NoisyDense(self.nb_actions)(adv)
else:
adv = Dense(self.nb_actions)(adv)
(略)
else:
c = Dense(512, activation="relu")(c)
if self.enable_noisynet:
c = NoisyDense(self.nb_actions, activation="linear")(c)
else:
c = Dense(self.nb_actions, activation="linear")(c)
return Model(input_, c)
def forward(self, observation):
(省略)
# 行動を決定
# noisy netが有効の場合はそちらで探索する
if self.training and not self.enable_noisynet:
(ϵ-greedy法)
else:
(Q値で行動を決定)
(省略)
2019/5/30 追記:NoisyNetの修正
コメントを頂き動かす事が出来ました!
※GitHubGistとGoogleColaboratoryのコード全体には反映できていない内容です。
頂いた下記リンクを元に以下のように修正しました。
https://github.com/keiohta/tf2rl/blob/atari/tf2rl/networks/noisy_dense.py
#copy from https://github.com/OctThe16th/Noisy-A3C-Keras
class NoisyDense(Layer):
(略)
def build(self, input_shape):
assert len(input_shape) >= 2
self.input_dim = input_shape[-1]
# 2行追加
self.kernel_shape = tf.constant((self.input_dim, self.units))
self.bias_shape = tf.constant((self.units,))
(略)
def call(self, X):
# この行を書き換え
perturbation = self.sigma_kernel * K.random_uniform(shape=self.kernel_shape)
#perturbation = self.sigma_kernel * self.epsilon_kernel
perturbed_kernel = self.kernel + perturbation
output = K.dot(X, perturbed_kernel)
if self.use_bias:
# この行を書き換え
bias_perturbation = self.sigma_bias * K.random_uniform(shape=self.bias_shape)
#bias_perturbation = self.sigma_bias * self.epsilon_bias
perturbed_bias = self.bias + bias_perturbation
output = K.bias_add(output, perturbed_bias)
(略)
学習が進むことは確認しています。
Categorical DQN
よく分かりませんでした…
実装例も少なく…、今回は保留とします。
参考
・【論文】A Distributional Perspective on Reinforcement Learning (C51/Distributional RL; 2017)
Pendiumゲームで学習
PendulumProcessorForDQN の修正
画像ありの学習がうまくいかなかったので少し修正します。
やることは、画像処理の軽量化と報酬の正規化です。
class PendulumProcessorForDQN(rl.core.Processor):
def __init__(self, enable_image=False, image_size=84):
self.image_size = image_size
self.enable_image = enable_image
self.mode = "train"
def process_observation(self, observation):
if not self.enable_image:
return observation
return self._get_rgb_state(observation) # reshazeせずに返す
def process_action(self, action):
ACT_ID_TO_VALUE = {
0: [-2.0],
1: [-1.0],
2: [0.0],
3: [+1.0],
4: [+2.0],
}
return ACT_ID_TO_VALUE[action]
def process_reward(self, reward):
if self.mode == "test": # testは本当の値を返す
return reward
# return np.clip(reward, -1., 1.)
# -16.5~0 を -1~1 に正規化
self.max = 0
self.min = -16.5
# min max normarization
if (self.max - self.min) == 0:
return 0
M = 1
m = -0.5
return ((reward - self.min) / (self.max - self.min))*(M - m) + m
# 状態(x,y座標)から対応画像を描画する関数
def _get_rgb_state(self, state):
img_size = self.image_size
h_size = img_size/2.0
img = Image.new("RGB", (img_size, img_size), (255, 255, 255))
dr = ImageDraw.Draw(img)
# 棒の長さ
l = img_size/4.0 * 3.0/ 2.0
# 棒のラインの描写
dr.line(((h_size - l * state[1], h_size - l * state[0]), (h_size, h_size)), (0, 0, 0), 1)
# 棒の中心の円を描写(それっぽくしてみた)
buff = img_size/32.0
dr.ellipse(((h_size - buff, h_size - buff), (h_size + buff, h_size + buff)),
outline=(0, 0, 0), fill=(255, 0, 0))
# 画像の一次元化(GrayScale化)とarrayへの変換
pilImg = img.convert("L")
img_arr = np.asarray(pilImg)
# 画像の規格化
img_arr = img_arr/255.0
return img_arr
NNモデルの Dense Units のハイパーパラメータ化
DQN では Dense 層のユニット数が 512 ですが、学習時間の関係で減らしたいときがちょくちょくありました。
(今回のようなシンプルなゲーム等)
ですのでハイパーパラメータ化して外に出しています。
コードは置き換えているだけなので省略します。
画像なしによる学習
ハイパーパラメータの数がやばいですね…
学習の書き方は前回とほぼ一緒です。
まずは画像なしバージョンです。
import gym
from keras.optimizers import Adam
# 別ファイルにあると仮定しています。コード全体では1つのファイルにまとめています。
from PendulumProcessorForDQN import PendulumProcessorForDQN
from RainbowAgent import RainbowAgent
env = gym.make("Pendulum-v0")
nb_actions = 5 # PendulumProcessorで5個と定義しているので5
processor = PendulumProcessorForDQN(enable_image=False)
# 引数が多いので辞書で定義して渡しています。
args={
"input_shape": env.observation_space.shape,
"enable_image_layer": False,
"nb_actions": nb_actions,
"window_length": 1, # 入力フレーム数
"memory_max_size": 10_000, # 確保するメモリーサイズ
"nb_steps_warmup": 200, # 初期のメモリー確保用step数(学習しない)
"target_model_update": 100, # target networkのupdate間隔
"action_interval": 1, # アクションを実行する間隔
"train_interval": 1, # 学習する間隔
"batch_size": 64, # batch_size
"gamma": 0.99, # Q学習の割引率
"initial_epsilon": 1.0, # ϵ-greedy法の初期値
"final_epsilon": 0.1, # ϵ-greedy法の最終値
"exploration_steps": 5000, # ϵ-greedy法の減少step数
"processor": processor,
# 今回追加分
"memory_type": "per_proportional", # メモリの種類
"per_alpha": 0.6, # PERの確率反映率
"per_beta_initial": 0.4, # IS反映率の初期値
"per_beta_steps": 5000, # IS反映率の上昇step数
"per_enable_is": False, # ISを有効にするかどうか
"multireward_steps": 3, # multistep reward
"enable_double_dqn": True,
"enable_dueling_network": True,
"enable_noisynet": False,
"dence_units_num": 64, # Dence層のユニット数
}
agent = RainbowAgent(**args)
agent.compile(optimizer=Adam()) # optimizerはAdamを指定
print(agent.model.summary())
# 訓練
print("--- start ---")
print("'Ctrl + C' is stop.")
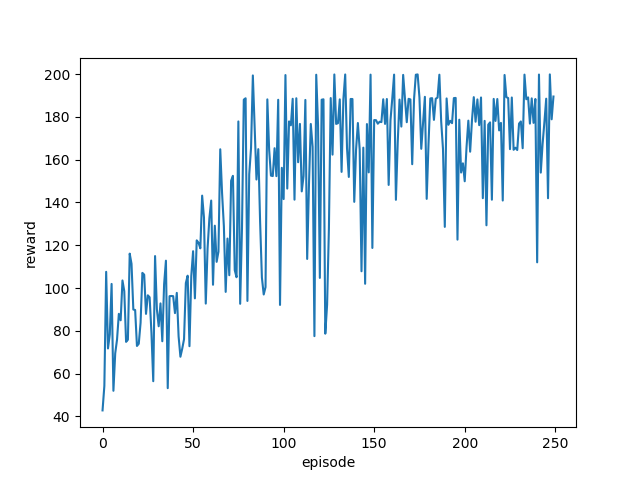
history = agent.fit(env, nb_steps=100_000, visualize=False, verbose=1)
# 結果を表示(stepを削除しています)
plt.subplot(1,1,1)
plt.plot(history.history["episode_reward"])
plt.xlabel("episode")
plt.ylabel("reward")
plt.show()
# 訓練結果を見る
processor.mode = "test" # 本来の報酬を返す
agent.test(env, nb_episodes=5, visualize=True)
ISはもっと長期的な学習に効果があるっぽいので切っています。
また、NoisyNetは実装に自信がないので切っています。。。
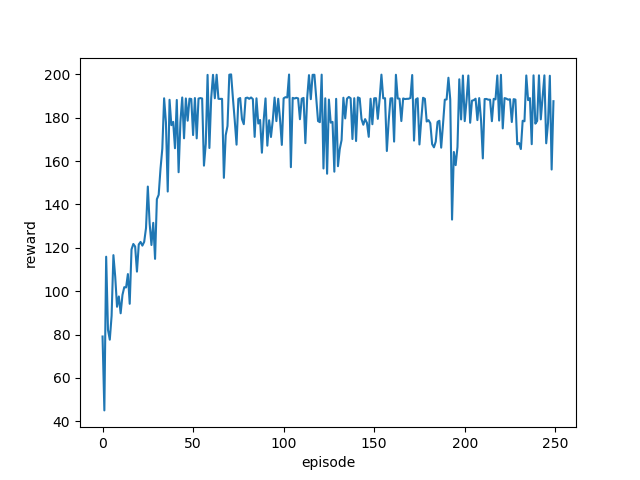
結果
ちゃんと学習できていますね。
画像ありによる学習
こちらも前回と同じです。
パラメータや画像ありへの変更箇所は、コード全体の GitHubGist や GoogleColaboratory を参照してください。
結果
ちゃんと学習できていますね。
まとめ
こうして見るとまだまだ改良の余地が多くて発展途上なアルゴリズムだなって思いますね。
次はApe-Xを実装したいと思います。