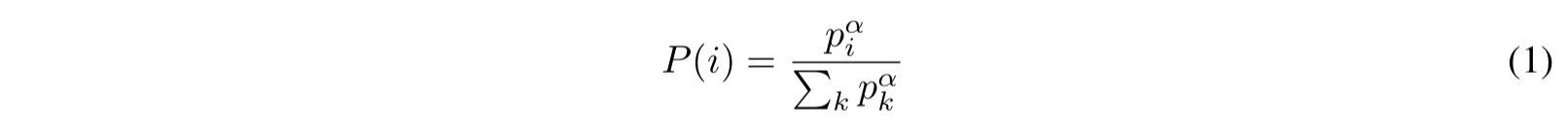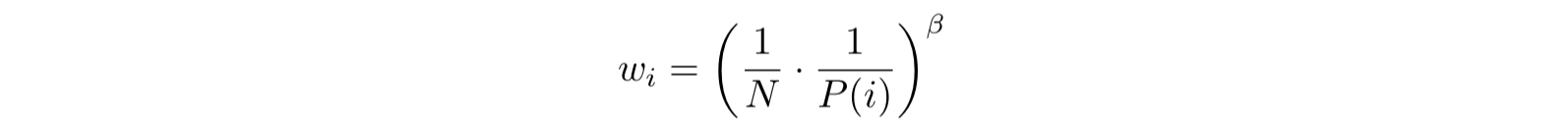【論文】Prioritized Experience Replay (2016)

とても有名な手法なので巷にたくさん情報ありますが。

[1511.05952] Prioritized Experience Replay

メタ情報

• ICLR 2016
• Google DeepMind

概要

• 経験再生の際は各経験の重要性を考えてサンプリングすべきである
• DQN と組み合わせることで Atari で state-of-the-art ¹

導入

• 経験再生は、標本の i.i.d. の仮定と、有用なサンプルの再利用とサンプル効率にとって良い方法
• さらに優先度をつけることで、「驚き」「冗長性」「タスク依存」などの要素を考えることができる。また、今は重要なサンプルでなくてもエージェントが賢くなったら重要になるかも知れない
• TD誤差で優先度をつける
  • サンプルの多様性が失われるが、これは確率的優先度で対処
  • バイアスが生まれるが、これは重要度サンプリングで対処

背景

• 多くの脳科学研究で、げっ歯類の海馬では優先度付き経験再生 (PER) がおこなわれていることが実証されている
  • 優先度は、報酬やTD誤差で決まることが報告されている
• model-based planning ではすでに PER が使われているが、我々はこれを更に頑健に工夫して model-free RL に応用する
• TD誤差は経験再生だけではなく探索や特徴量選択にも利用されている

経験再生

動機

• "Blind Cliffwalk" (目隠し崖歩き) の例を考える
  • 報酬がレアで探索が難しいチャレンジングな問題
  • 最初の非ゼロ報酬がもらえるのは n ステップ後、つまり n に関して指数的な回数の探索が必要となる
    • 言い換えれば、ランダム探索で報酬が貰える確率は $2^{-n}$
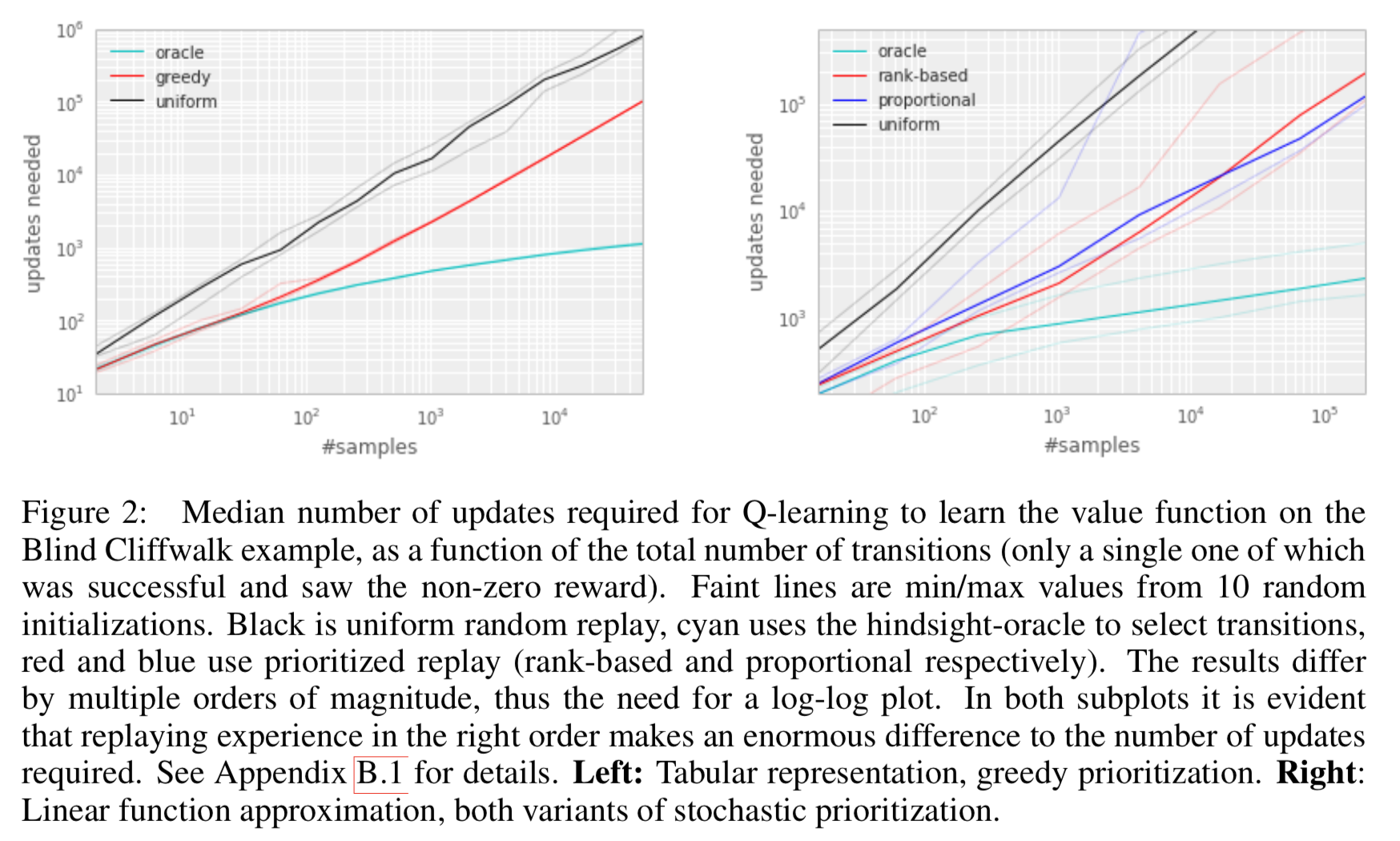
• Q学習で経験再生する際に、uniform (つまり経験再生からのランダムサンプリング；従来手法) と、oracle (一番ロス関数が減少するサンプルを (チートして) 選択) で比較
• 確かに良い結果が得られる (Figure 1)。軸が log-log スケールであることに注意せよ

TD誤差による優先度

• 理想的には、エージェントがそのサンプルからどれだけ学習できるかが優先度の基準
  • TD誤差 $\delta$ (の絶対値) でこれを代用する
• "greedy TD-error prioritization" アルゴリズムで実験 (Figure 2 left)
  • TD誤差の大きな順にサンプリングするだけ
  • Q値の初期値はゼロにしてはいけない。ランダムもしくは楽観的初期化をせよ。初期値がゼロだと、すべてのTD誤差がゼロである
  • 優先度はバイナリヒープで実装 (最大要素のサンプリングが O(1)、TD誤差の更新が O(logN))。実装の詳細は付録B.2.1

確率的優先度

• TD誤差による優先度では、最初に計算されたTD誤差が小さいサンプルはリプレイされづらくなる問題がある
  • スパイクするようなエラー (報酬に起因するかもしれないし、関数近似に起因するかもしれない) にも弱い
  • TD誤差の大きなサンプルばかり選ばれて多様性が失われ過学習のおそれ
• そこで、TD誤差の大きな順に選ぶ (greedy) ではなく、TD誤差の大きな順に大きな確率で選ぶ (stochastic) ようにする
  • 
  • $p_i$ がサンプル i の優先度、 $P(i)$ がサンプリング確率
• ナイーブな方法 (proportional)：
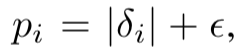
• 順位ベースの方法 (rank-based)：
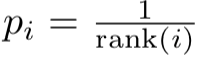
  • この場合 $P$ はパラメータ $\alpha$ の power-law 分布となる
  • より外れ値に頑健
• 両方の比較は Figure 2 (right)

実装

• proportional
  • "sum-tree" (各ノードの値は子孫の和となる) を使うと効率的である (詳細は付録 B.2.1)
• rank-based
  • 累積分布をそれぞれ同じ確率になるように k 個のセグメントに区切る (このセグメントの境界は N や α が変化しない限り変わらない)
  • 各セグメントをサンプリングし、その中からさらに標本をサンプリングするようにする
    • ミニバッチサイズを k に合わせると便利である
    • バッチデータをバランシングする効果がある (層化抽出法 - Wikipedia)

バイアスの焼きなまし

• PER はデータの分布を変えてしまうので、推定している期待値にバイアスを入れてしまう
  • 重要度サンプリングで対処
    • 
    • $\beta = 1$ のとき完全な補正となる
• 安定性のため、 $\frac{1}{\max_i w_i}$ でスケーリングする
• 実験の結果、重要度サンプリングをおこなうと学習の立ち上がりが遅くなる一方で最終的な結果がよくなる可能性が示された (figure 12)
  • そこで、 $\beta_0 < 1$ を初期値として、訓練の最後に 1 になるように線形に焼きなます方法を採用
• 重要度サンプリングは非線形近似という観点からも有用
  • 勾配は1次情報なので局所的にしか有効ではない。あまり大きく値を変えすぎると近似がおかしくなる
  • PER では重要なサンプルが何度も勾配計算される一方で重要度サンプリングによってそのサンプルによる更新量が制限され、相性が良い ²

実験

• Nature 版 DQN および Double DQN と比較
  • リプレイサイズ：10^6
  • ミニバッチサイズ：32
  • パラメータの更新は4ステップごと ³
  • 報酬とTD誤差は [-1, 1] にクリッピング
  • PER では学習率を $\eta / 4$ に設定
    • 優先度の高いサンプルは典型的には大きな勾配を持つことへの対処
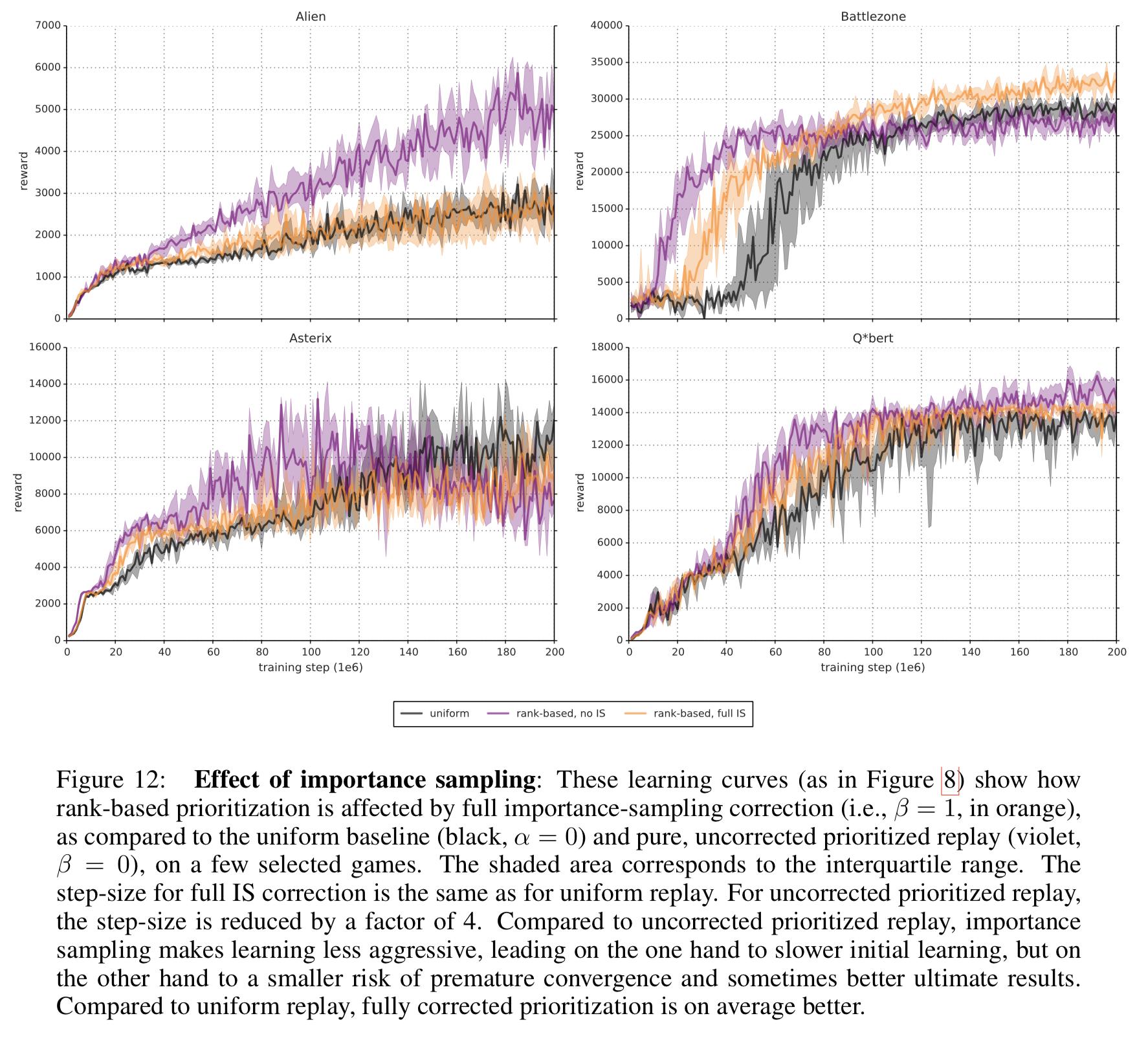
• サマリのプロットは Figure 4 (詳細は Figure3, 7, 8, Table 1, 6, 7 を見よ)

議論

• rank-based 法は、エラーのスケールや外れ値への頑健性、ヘビーテールによるサンプルの多様性の確保、層化抽出法によるミニバッチの安定等で良いと期待できる
  • 逆にエラースケールを無視していることで、疎な報酬の環境でうまくいかない可能性もある
• しかし実際には proportional も rank-based もうまくいく
  • DQN そのものの error/reward clipping が効いていると思われる

拡張

優先度付き教師付き学習

• クラスバランスが異なるような教師付き学習の問題でも、誤差関数の値を優先度として用いれば、レアなクラスの誤差はなかなか小さくできないため、優先度の効果で自然にクラスバランスが揃うのではという直感
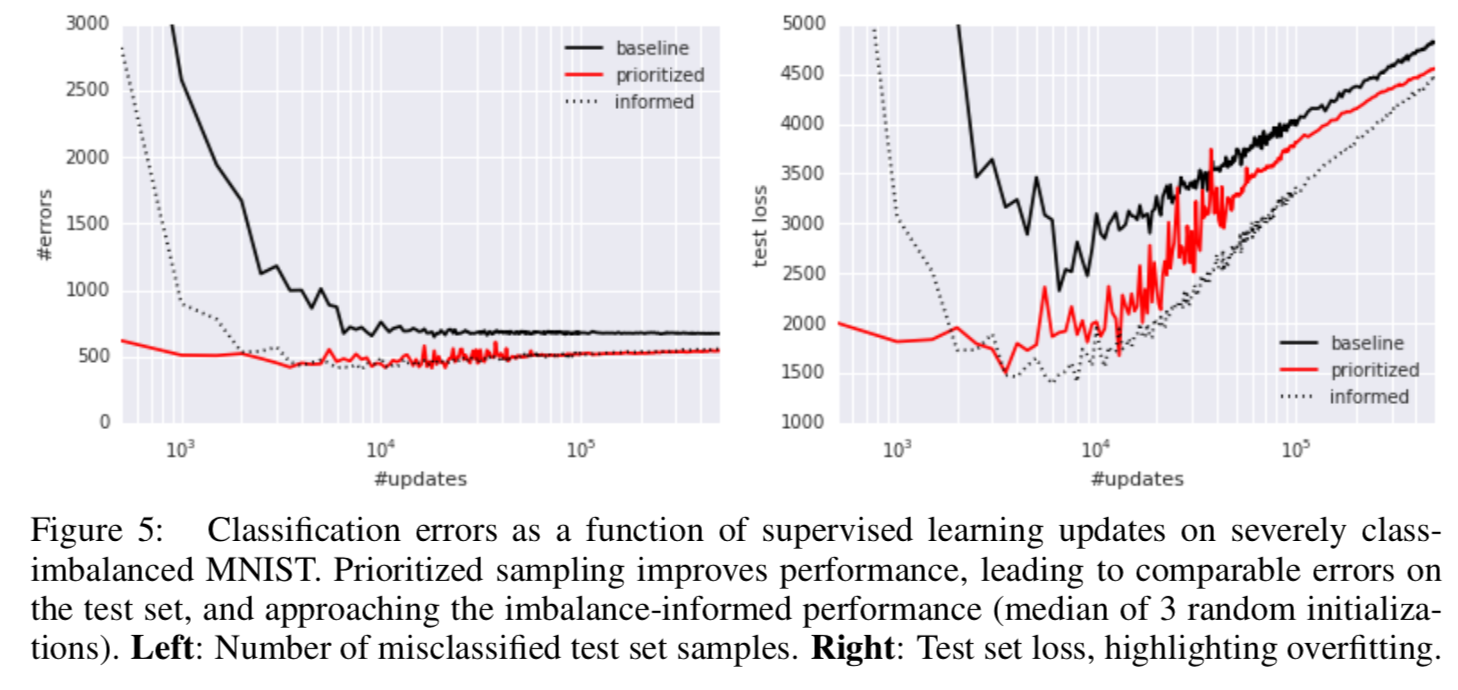
  • MNIST のクラスバランスを偏らせて予備実験してみた (0, 1, 2, 3, 4 のサンプルを訓練データから99%除去した)
• 結果は Figure 5
  • baseline: そのまま学習
  • prioritized: 優先度付き
  • informed: 除去したクラスの誤差の重みを補正 (100倍)

方策オフ再生

• 方策オフ強化学習のアプローチは大きく2つ
  • rejection sampling
  • 挙動方策と推定方策の違いを吸収するための重要度サンプリング ⁴
• PER のパラメータ $w, \alpha, \beta$ を適当にいじると、上記2アプローチと同一手法となる
• 経験上はその中間くらいのパラメータがうまくいく

探索フィードバック

• PER の各サンプルの再生回数がエージェントにとっての有用性を示していると考えられるので、探索パラメータ ( $\epsilon$ とかボルツマン分布の温度とか好奇心パラメータとか) を再生回数でパラメタライズされた分布から生成すると良さそうですね

優先度付きメモリ

• サンプリングだけではなく、どのサンプルをメモリに残しておくかも優先度をつけても良さそうですね
  • よく探索される遷移は誤差が小さくなるはずなので、そういったサンプルの多くがメモリから消去されて効率的になる ⁵

優先度基準の派生

(一部抜粋)

• TD誤差の符号によって優先度を変える (絶対値ではなく非対称にする) のはありうる
  • ネズミの研究でも観測されているらしい
• 脳科学の研究では、1遷移ではなくエピソード全体の報酬で優先度付けしているというエビデンスが得られている
• サンプルの多様性 (過学習や局所解を防ぐ効果) を保つため、優先度に「novelty (目新しさ)」を導入することも考えられる
  • もしくは、しばらくサンプルされていない遷移の優先度を上げる、ということもアリ

参考資料

• [1511.05952] Prioritized Experience Replay
• Prioritized Experience Replay - DeepLearningを勉強する人

1. 当時 ↩

2. つまり、パラメータを大きく変えたい場合はある点で計算した勾配で一気に更新するのではなく、少しずつ進めながら各地点での勾配情報を採用していくべきである。そしてその方法がまさにここで提案している方法によって実現される (少しずつ進めながら＝重要度サンプリング、各地点での勾配情報＝優先度) ↩

3. 確信はないが、Atari での DQN では行動を4回繰り返す (そして state も4フレームぶんスタック) のが普通なので、結局エージェントからは1ステップごととして見える？ ↩

4. 原文「Two standard approaches to off-policy RL are rejection sampling and using importance sampling ratios ρ to correct for how likely a transition would have been on-policy.」訳は一部補っていますので、もしかしたら誤解があるかもしれません。 ↩

5. (解釈間違っていたらすみません) PER の文脈では、誤差の小さなサンプルは優先度が低いのでサンプリング確率も低い。誤差の小さなサンプルというのは大抵は典型的な遷移の似たようなサンプルになりがちであるため、そういったサンプルをメモリに残しておく必要はそんなにない。 ↩