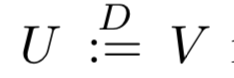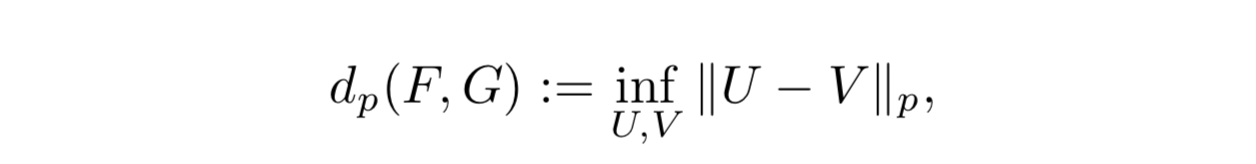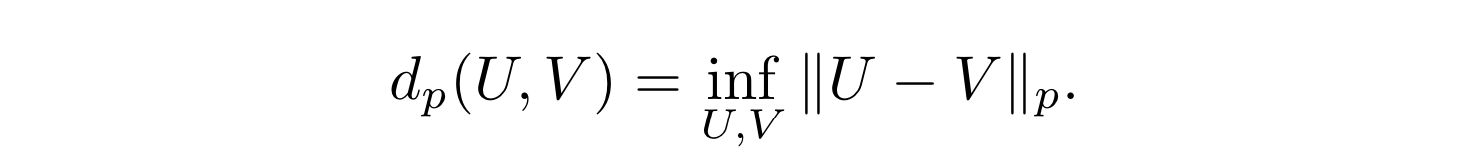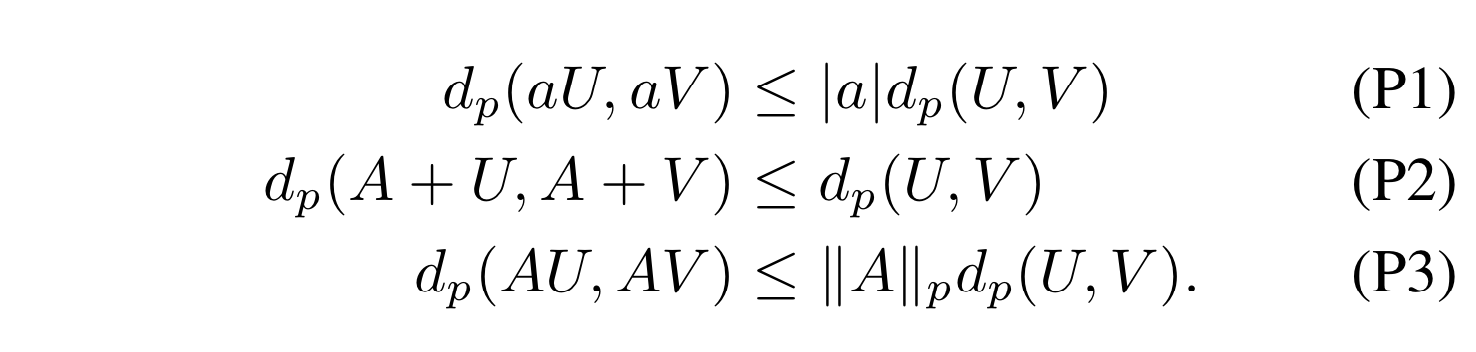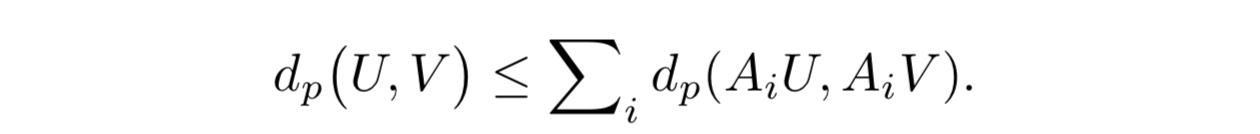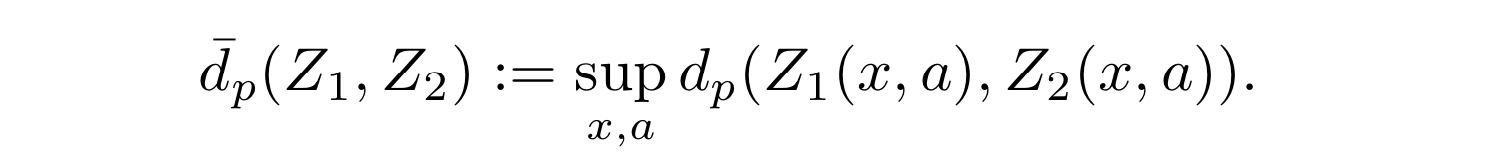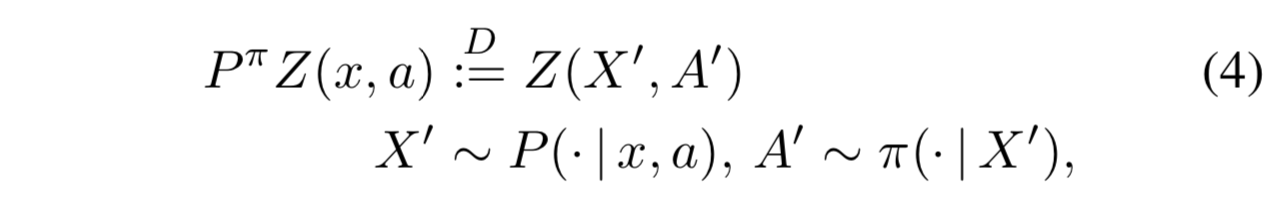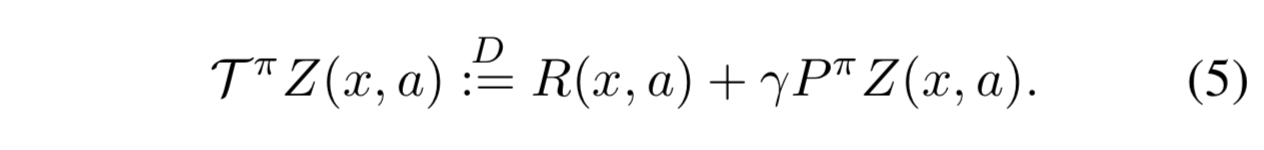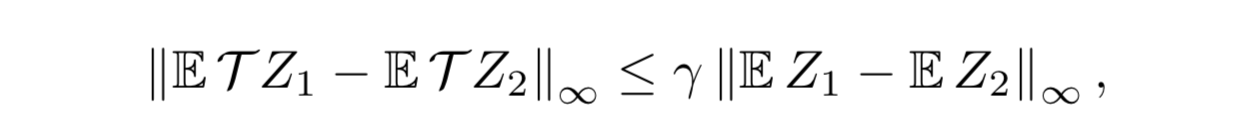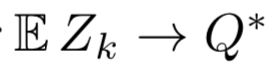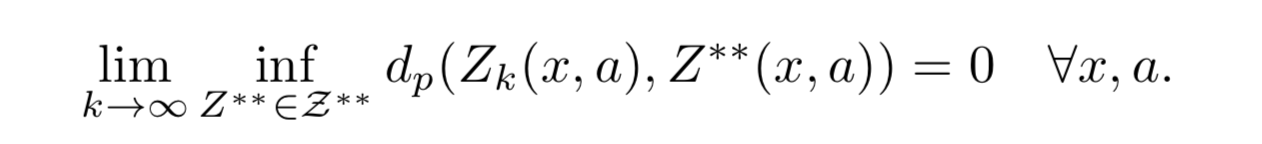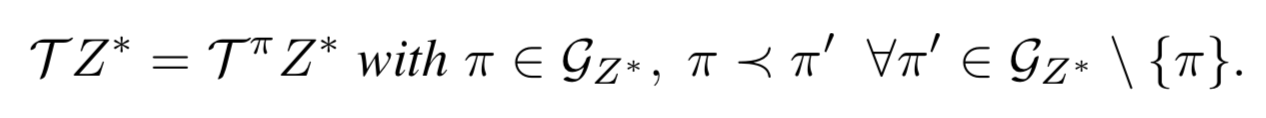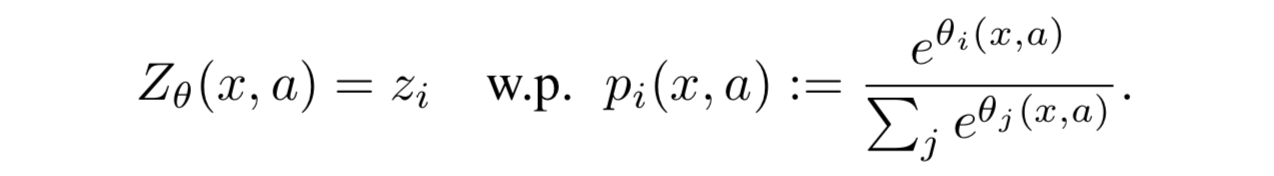[1707.06887] A Distributional Perspective on Reinforcement Learning

https://t.co/d9rupDKeCk
A Distributional Perspective on Reinforcement Learning (C51/Distributional RL; 2017)
— keisuke-nakata (@nakata_k2) 2018年12月18日

メタ情報

「C51」と呼ばれる手法 (あるいは、「Distributional RL」「Distributional DQN」と言ったときもこの手法を指している可能性があるが、それらは現在はもう少し広範な意味で使われるため、より具体的な手法名の「C51」と呼んだほうが誤解が少ないと思われる)
ICML2017 https://icml.cc/Conferences/2017/Schedule?showEvent=580
Bellemare 氏筆頭に DeepMind の方々
- Bellemare 氏は ALE を作った人なので、深層強化学習の今日の発展に大きく寄与した一人
  - 2018年9月現在は Google Brain に在籍している様子
この論文から発展した手法が現在色々提案されている¹。例えば、
- [1710.10044] Distributional Reinforcement Learning with Quantile Regression
- [1806.06923] Implicit Quantile Networks for Distributional Reinforcement Learning
- [1804.08617] Distributed Distributional Deterministic Policy Gradients
- よって、現在でもこの論文が state-of-the-art というわけではないだろうが、Rainbow の構成要素として利用されているし、distributional の系譜の祖先としても、分布型価値関数の多くの定理への理論的な貢献からも読む価値はあるはず

概要

強化学習において、収益の 期待値 ではなく、その分布が有用であることを主張する
収益の分布を用いた形式のベルマン方程式を解析し、理論的な成果を得た
また同時に Atari 環境において実験的な成果も確認した

導入

期待値が Q となるような価値分布 Z を再帰的に記述する分布型ベルマン方程式 (distributional Bellman equation) を考える
ベルマン方程式を分布で考えるというアイデアはベルマン方程式そのものと同じくらい歴史があるが、これまではあまり脚光を浴びていなかった

方策評価ベルマン作用素の縮小性

価値分布に関するベルマン作用素は、方策を固定すると、Wasserstein 距離において縮小写像となる
- KL divergence や Kolmogorov 距離ではそうではない

よりよい近似

分布で近似すると、多峰性や方策の非定常性といった部分に対してアルゴリズムとして強くなるはずである

設定

(標準的な強化学習の問題設定の説明がされているため、特に必要そうな部分以外略)

報酬関数 R は明示的に確率変数として捉える ²
通常の記法同様、Q や Z の右肩に π を乗せたものは方策 π の価値であり、* を乗せたものは最適価値 (ベルマン方程式の停留点)

分布型ベルマン作用素 (distributional Bellman operator)

(論文中では確率測度の話が挟まっているが、直感的な理解に支障はないので略)

という表記は「確率変数 U が V と同じ分布に従う」ということを示す

Wasserstein 距離

累積分布関数 F と G のあいだの Wasserstein 距離は次のように定義される
- ただし U と V はそれぞれ F と G を累積分布関数に持つような確率変数
正確な記法ではないが、わかりやすさのため、次のようにも表記する：
スカラ a と、U および V と独立な確率変数 A に関して、次の特性を持つ：
さらに、いくつかの補題も利用する (証明は付録)

補題1 (分割補題)

標本空間 Ω の分割を表す確率変数 $A_{i}$ に関して次が成立

補題2

(モーメントがバウンドされた) 2つの価値分布 Z1 と Z2 に関して次のように定義する：
- この $\overline{d}_p$ は分布型ベルマン作用素の収束性の証明に用いる
- $\overline{d}_p$ は価値分布のメトリックになっている

方策評価

ここで考える $Z^\pi$ は、環境の不確実性というよりも、エージェントの不確実性を表すもの
遷移作用素 $P^\pi$ を次のように定義する³：
- X と A が大文字なのは、確率変数であることを強調するため
分布型ベルマン作用素 $\mathcal{T}^\pi$ を次のように定義する：
(5) はよくみるベルマン作用素に似ているが、次の点で異なる：
- 報酬 R のランダム性
- 遷移 $P^\pi$ のランダム性
- 次の状態価値 $Z(X', A')$ が分布である
続いて、この分布型ベルマン作用素が $Z^\pi$ なる唯一の不動点を持つ縮小写像であることを示す

$\overline{d}_p$ における縮小性

補題3

$\mathcal{T}^\pi$ は $\overline{d}_p$ において $\gamma$ -縮小である。つまり、指数的に収束する

補題3から、バナッハの不動点定理により、分布型ベルマン作用素が $Z^\pi$ なる唯一の不動点を持つ縮小写像であることが示された。また、KL divergence や Kolmogorov 距離を計量に用いると縮小写像にならないことがわかっている

中心モーメントにおける縮小性 ⁴

$\mathcal{T}^\pi$ は p-次中心モーメント (p>2) で縮小性があるとは限らないが、 $\{Z_k\}$ の指数的な収束性は証明できる

制御

これまでは方策 π を固定して考えたが、ここからは π 自体も変化させる問題設定 (＝制御) を考える
最適価値分布は一般には複数存在する
ベルマン最適作用素が弱い意味で最適価値分布に収束することを示す
- しかし、この作用素はどんなメトリックに対しても縮小性を持ってはいない

定義1 (最適価値分布)

最適価値分布とは、最適方策 $\pi^*$ の価値分布のことである

定義2 (欲張り方策)

(現在の) 価値分布 Z に関する欲張り方策 π とは、Z の期待値を最大化するような方策のことである⁵：

補題4

(モーメントがバウンドされた) 価値分布 Z1 と Z2 を考えると次が成立する：
- 特に、は指数的に収束する
  - ここでいう $Z_k$ は分布型ベルマン最適作用素 $\mathcal{T}$ を適当な初期分布 $Z_0$ に繰り返し作用させたもののこと。つまり、分布型ベルマン最適作用素を用いて価値分布を更新すると、その期待値は最適価値に指数的に収束するということを言っている
補題4を見ると、 $Z_k$ は $\overline{d}_p$ においてある不動点に高速に収束することを期待するが、残念ながら、収束は高速ではないし、不動点の保証もない ⁶
- 実際に望めるのは各点収束であり、しかも非定常最適価値分布 (nonstationary optimal value distributions) への収束である

定義3

非定常最適価値分布 (nonstationary optimal value distributions) $Z^{**}$ とは、最適方策列に対応する価値分布である

定理1 (制御設定における収束性)

X が可測で A が有限とする。すると次が成立：
- X が有限の場合、一様収束性がある
  - さらに、Π* に全順序がある場合次が成立：
    - (Zにおける欲張り方策による遷移を考えると不動点がある、くらいの意味か。自信ない)
$Z_k$ の平均値は $Q^*$ に指数的に収束するが、分布自体の振る舞いはよくわからない

命題1

作用素 $\mathcal{T}$ は縮小写像ではない
上の Figure 2 の例で考えると、Z と Z* との距離は
で与えられるが、それぞれに T を作用させてからもう一度距離を取ると
となり、縮小していないことがわかる。これは縮小性の反例になっている

命題2

すべての最適作用素 $\mathcal{T}$ が不動点を持つとは限らない ⁷

命題3

$\mathcal{T}$ が不動点を持つことは $\{Z_k\}$ の $\mathcal{Z}^*$ への収束を保証するものではない

近似分布学習

パラメトリック分布

Vmin から Vmax の間を N 等分したヒストグラムによる分布の近似をおこなう
各ビン (論文中では「atom」と呼んでいるので今後それに従う) の高さ p (＝ヒストグラムの高さなので、つまり離散確率値) を次のようにモデル化⁸：

射影ベルマン更新

離散分布を用いるため、 $\mathcal{T}Z_\theta$ と $Z_\theta$ の共通サポートがなくなってしまうが、Wasserstein 距離を用いるため問題にならない ⁹
- しかし、遷移の標本からしか訓練できないので、実際には Wasserstein 損失が計算できない
代わりに、 $\hat{\mathcal{T}}Z_\theta$ を $Z_\theta$ のサポートに射影して多クラス分類を解く
まずベルマン更新 $\hat{\mathcal{T}}z_j := r + \gamma z_j$ を各 atom $z_j$ に対して実施し、その後で各 atom に対して $\hat{\mathcal{T}}z_j$ の隣接要素で確率を更新する
- そして、このカテゴリカル分布間のロスを取れば良い：
  - - 実験の章でも説明があるが、この $\tilde{\theta}$ は target network のパラメータのはず
- (何を言っているのかわかりにくいと思うので、以下に私の注を入れます)
  - Figure 1 を参照するのがわかりやすいです
  - まず、 (a) の $P^\pi Z$ は、Z からの遷移先における価値分布のことです。従来のQ学習で言うなら $Q(s_{t+1}, a_{t+1})$ のこと
  - (b) 割引率 γ をかけて、分布をゼロ方向に縮めます。 この時点で、atom のビン幅が崩れいていることに注意!
  - (c) 得られた報酬 R を足して、平行移動します
  - (d) この Φ が曲者かと思いますが、これは、(b) で崩れたビン幅を、もとのビン幅に戻す処理をしているだけです (私の理解が間違っていなければ)。このビン幅をもとに戻す処理が、サポートを射影する処理にあたります (同じビン幅をもったヒストグラム同士で比較できるようにする)。各ビンの高さ (確率 p) もビン幅と同時に調整しますが、これはできるだけ同じ高さになるようにすればよいです。この処理を式で書くと (7) みたいになる模様。
これらのアルゴリズムは Wasserstein 距離を使っていないが、深い繋がりは示唆されている
アルゴリズムは下記の通り：

Atari における評価

ベースは DQN
5種類のゲーム (Fig.3 参照) で準備実験をしてパラメータを決定
- $V_{\text{MAX}} = -V_{\text{MIN}} = 10$

↑ Space Invaders で学習した報酬分布の例。レーザーを撃つにはタイミングが早いため、(Laser, Left+Laser, Right+Laser) は Return がほぼゼロに張り付いている一方で、その他の行動は分布としての Return を保持している。筆者らはこれは単なる期待値では表現できない情報、つまりこの場合は期待値ゼロの場合は分布として潰れているけどそれ以外ではいろんな可能性がある、という情報を保持していると主張している

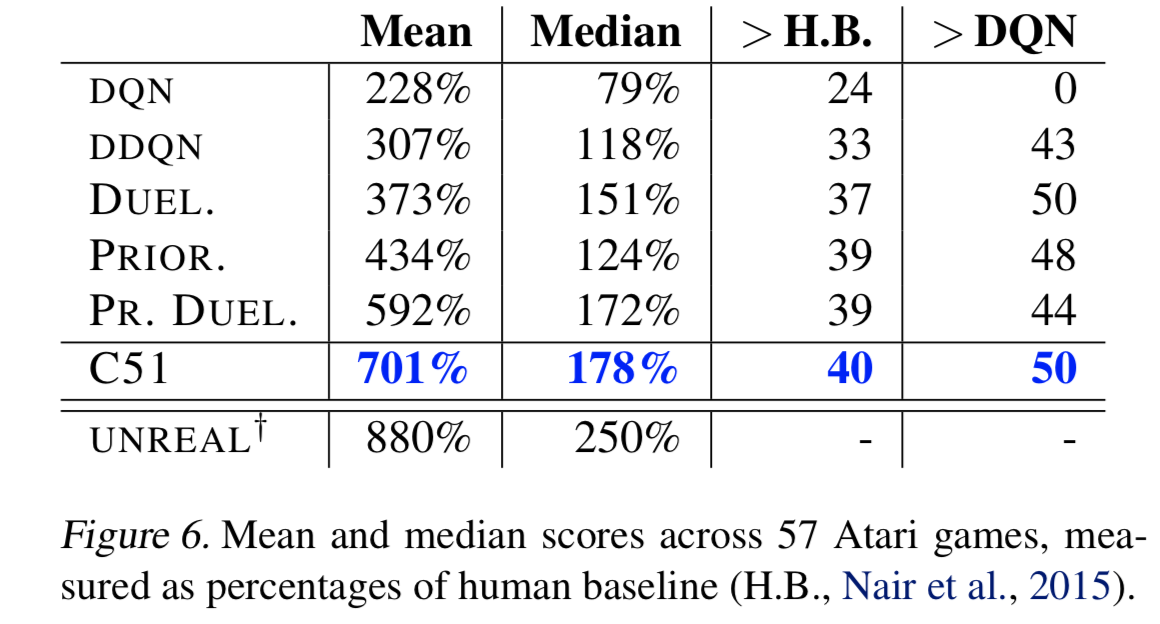
予備実験では atom の個数を 51 にしたものが一番良かった。この設定のアルゴリズムを C51 と呼ぶこととする

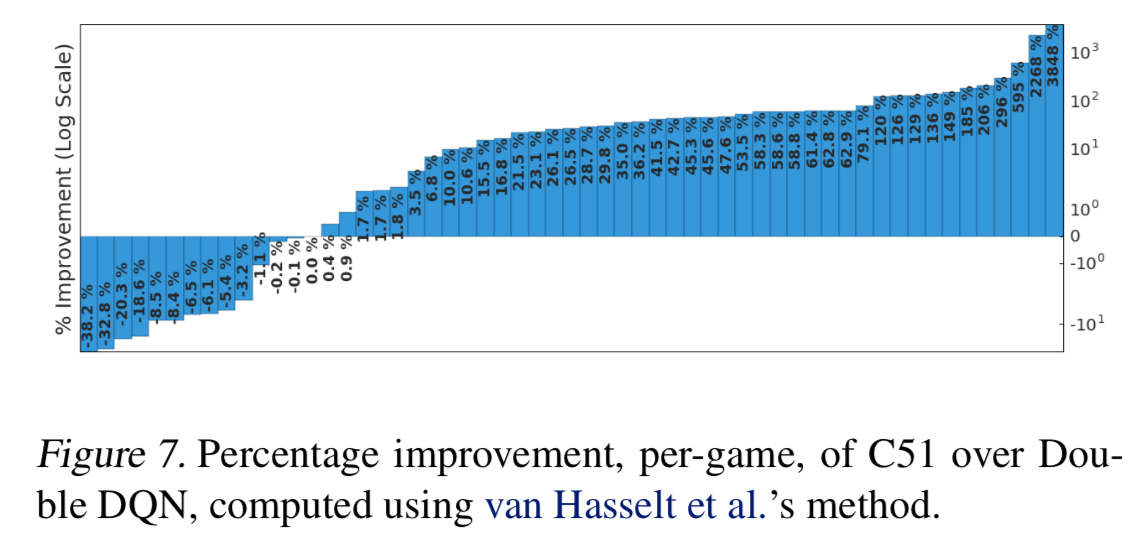
C51 は state-of-the-art を達成
- $\epsilon$ の値を下げて実験していることに注意
特に、Venture や Private eye のような疎な報酬のゲームに強かった
- 価値分布はめったに起こらないイベントを伝播しやすいという特性を持つことを示唆

※論文中の最後に掲載されている Figure 15-18 もとても興味深いが、ここでは割愛

議論

なぜ分布を学習することが効果的なのかについての考えうる理由の概略を説明する

chattering の抑制

ベルマン最適作用素の非定常性と、関数近似を組み合わせたときに、方策の収束が妨げられることを chattering と呼ぶ
分布の学習によって、conservative policy iteration と同じような効果が得られているのではないか

より大きな予測空間

分布として捉えるため、エージェントが不完全でもより多くの情報を得ることができる

帰納的なバイアスのフレームワーク ¹⁰

DQN で価値関数をクリッピングすると性能が落ちるが、C51ではそうではない。つまりC51では外れ値になるような値をクリッピングした最適化問題を解くことが許される

良い振る舞いの最適化

カテゴリカル分布の KL divergence は最小化しやすいことが知られている
- 研究の初期段階では連続密度の KL divergence を試したがうまくいかなかった

参考資料

感想

理論的な章 (chapter3) の理解が後半から相当怪しい。論文中では数式だけではなく解釈も入れてくれているが、細かい部分があまり理解できていない
モチベーションと理論背景、実験結果がすべてガッチリまとまっていてステキ

進化の系譜がよくわかっていないので、時系列がおかしかったらすみません。また、Q値の分布を捉える、というアイデア自体は昔からあったようです。 ↩
そもそも報酬関数 R は確率的なのだが、期待値を取った形で計算してしまうことがほとんどなので、大抵の強化学習の問題設定ではあまり気にしていないと思う ↩
直感的には、 $P^\pi$ は、「状態 x で行動 a を取るときの価値分布」(左辺) は「状態 x で行動 a を取ったときに遷移した状態 X' と、現在の方策 π で選んだ X' における行動 A' における価値分布」(右辺) に等しい、ということを示すためのもの ↩
この節の理解はだいぶ怪しいので注意してください・・・ ↩
平たく言えば「Z が最大値をとるような行動を最大確率で取る」ような方策が欲張り方策。集合で定義されているのは、Z が最大となる点が複数存在するときに欲張り方策が一意に決まらないこともあるため ↩
だいぶ理解が怪しいが、期待値としての不動点 (最適価値) は存在してしかも指数的な収束をするが、期待値を取る前の分布としての収束に関してはそうではない、ということを言っているのだと思う ↩
ここの反例の示し方もよくわからない。T^nZ(x1) が Z*(x2, a1) と Z*(x2, a2) の値を振動するので不動点じゃない、というようなことを言っていて、直感的にも R(x2, a2) がどうなるかによって毎回 T^nZ(x1) の値も変わりそうだなぁと思うが、本文中で指摘している内容をちゃんと理解できていない ↩
つまり記事冒頭に貼った Figure 1 を例にすれば、ヒストグラムの横軸方向 (価値) が $z_i$ で、縦軸方向 (各価値となるような確率) が $p_i$ となっていて、 $i$ がそれぞれのビンを表していることになる ↩
共通のサポートがなくなる云々の話は、片方の分布の値がゼロになると KL ダイバージェンスの log の部分の処理ができなくなるけど Wasserstein 距離だとうまく定義できるという流れでよく見かけるものと同じことを言っていると思われる ↩
えいごがよくわからないので理解が怪しい ↩

【論文】A Distributional Perspective on Reinforcement Learning (C51/Distributional RL; 2017)